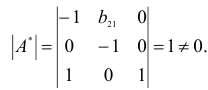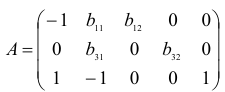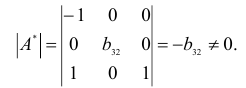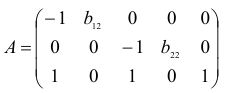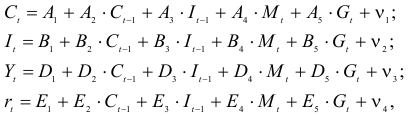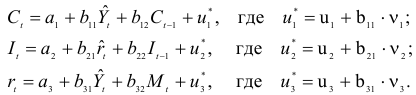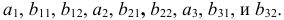Системы эконометрических уравнений
6.1. Системы уравнений используемых в эконометрике.В предыдущих параграфах рассмотрено моделирование экономических взаимосвязей одним уравнением. Однако, некоторые экономические процессы моделируется не одним, а несколькими уравнениями, содержащие как повторяющиеся, так и собственные переменные, описывающие многосторонние реальные взаимоотношения между экономическими показателями. В одних уравнениях определенная переменная рассматривается как факторный признак, а в другое уравнение эта переменная входит как результативный признак. Поскольку отдельные уравнения системы не могут рассматриваться изолированно друг от друга, то и деление переменных на зависимую и независимые теряет смысл. При рассмотрении систем эконометрических уравнений различают следующие переменные:
— эндогенные – это переменные, являющиеся экономическими факторами, которые описываются уравнениями модели, их значения зависят от внутренней структуры моделируемого экономического процесса;
— экзогенные, являющимися внешними наперед заданными экономическими величинами независимо от структуры модели, т. е. они задаются извне и объясняются экономическими факторами и закономерностями, находящимися за границами модели. Экзогенные переменные определяют эндогенные, но не находятся под их влиянием, т.е. между ними существуют только односторонние стохастические связи.
— предопределенные — переменные, значения которых отстают на один или несколько периодов, т.е. лаговые переменные. Лаговыми переменными могут быть: а) обычные экзогенные переменные, так как они определяются вне модели; б) лаговые экзогенные переменные, так как их значения принадлежат предшествующим периодам и определяются вне модели; в) лаговые эндогенные переменные, так как они определяются из предшествующей модели. Лаговые переменные можно отнести к заранее заданным экзогенным.
— совместно – зависимые переменные – это эндогенные переменные, которые определяются моделью, так как между ними существуют многосторонние связи, и они определяются не одним уравнением, а системой уравнений;
— возмущающие, или латентные переменные – это экономические факторы, не входящие в уравнения системы, но оказывающие влияние на совместно зависимые переменные, которые формируются за счет случайных влияний и ошибок, допущенных при построении модели.
Эконометрическая модель может быть представлена системами различных видов в зависимости от цели и задач исследования.
Структурная модель, записанная в матричном виде:
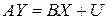
где 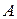
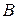
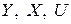
Структурная форма модели содержит всю существенную информацию об односторонних и многосторонних стохастических отношениях между экономическими факторами. Уравнения, составляющие эту модель, называются структурными уравнениями.
Если в структурной модели матрица 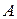
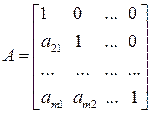
то соответствующая модель называется рекурсивной моделью.
Структурная модель, записанная в виде:
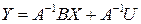
где 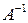
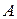
Если модель состоит только из уравнений, в каждом из которых только одна эндогенная переменная выражается через экзогенные переменные, то она называется системой независимых уравнений.
Рассмотрим примеры некоторых моделей.
1. Модель «Спрос – предложение».
Система одновременных уравнений используется при моделировании спроса – предложения в рыночных условиях. Предполагая, что спрос 
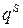
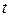
Уравнение (6.1) определяет функцию спроса, (6.2) — функцию предложения, (6.3) — условие равновесия. Наличие в уравнениях случайных отклонений 

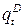
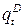
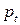
2. Кейнсианская модель формирования доходов.
Простейшая кейнсианская модель формирования доходов в предположении, что рассматривается закрытая экономика без государственных расходов, описывается системой одновременных уравнений вида:
Уравнение (6.4) описывает функцию потребления. (6.5) – макроэкономическое тождество. Переменные 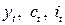
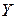
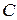
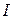
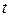
В кейнсианской модели формирования доходов, переменные 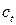
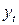
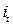
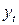
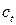
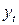
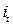


Коэффициент 
3. Модель IS – LM.
Простейшая модель равновесия на рынке товаров описывается системой одновременных уравнений вида:
Функция потребления: 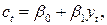
Функция налогов: 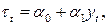
Функция инвестиций: 
Располагаемый доход: 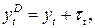
Государственные расходы: 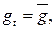
Макроэкономическое тождество: 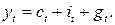
Переменные 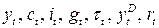
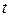
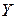
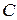
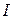
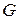
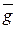
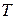
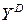
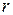
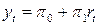
где 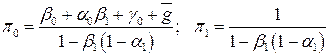
Линия равновесия на рынке денег (линия LM) определяет такое соотношение между процентной ставкой и уровнем дохода, при котором спрос на деньги равен их предложению. Одна из форм модели определяется следующей системой одновременных уравнений:
Функция спроса на деньги: 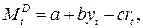
Функция предложения денег: 
Условие равновесия: 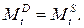
Разрешив (6.14) относительно 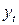
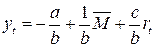
Точка пересечения кривых IS и LM определяет соотношение между процентной ставкой и уровнем дохода, при котором оба рынка находятся в состоянии равновесия. Эта точка находится из решения системы уравнений:
Структурные уравнения модели можно подразделить на поведенческие уравнения и уравнения – тождества. В поведенческих уравнениях описываются зависимости между переменными, а в уравнениях – тождествах соотношения, которые должны выполняться во всех случаях. Тождества не содержат подлежащие оценке параметры и случайные составляющие.
Уравнения, в которых эндогенные переменные выражены только через экзогенные или предопределенные переменные, а также случайные составляющие, называются приведенными уравнениями (уравнениями в приведенной форме). Предопределенными переменными называются лаговые эндогенные переменные, значения которых определены до рассмотрения уравнений. Например, уравнение спроса в модели «спрос – предложение» может быть представлено в виде:
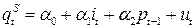
где переменная 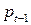
6.2. Проблема идентифицируемости модели. Необходимое и достаточное условие идентифицируемости.Изменение формы уравнений модели позволяет устранить проблему коррелированности факторных признаков и случайных отклонений, но может привести к другой проблеме – проблеме идентификации. Под идентификацией понимается возможность численной оценки параметров структурных уравнений по оценкам коэффициентов приведенных уравнений.
Исходную систему уравнений называют идентифицируемой (точно определенной), если по коэффициентам приведенных уравнений можно однозначно определить значения коэффициентов структурных уравнений. Однозначно определить коэффициенты структурных уравнений по коэффициентам приведенных уравнений можно в том случае, если количество уравнений, связывающих коэффициенты, равно количеству коэффициентов. Так, например, в модели Кейнса (6.6) – (6.7):

где 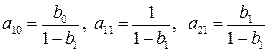
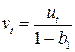
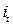
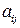
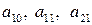
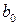
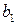
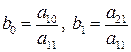
Исходную систему уравнений называют неидентифицируемой (недоопределенной), если по коэффициентам приведенных уравнений можно получить несколько вариантов значений коэффициентов структурных уравнений. Это случай когда число уравнений, связывающих коэффициенты, меньше числа определяемых коэффициентов.
Исходную систему уравнений называют сверхидентифицируемой (переоопределенной), если по коэффициентам приведенных уравнений невозможно определить значения коэффициентов структурных уравнений. В этом случае система, связывающая коэффициенты, несовместна.
Рассмотрим модель «спрос – предложение»
Построим приведенные уравнения, воспользовавшись условием равновесия (6.3):
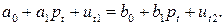
Последовательно разрешаем данное уравнение относительно 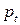
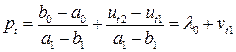
где 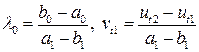
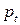
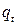
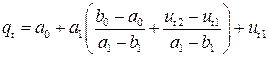

Система уравнений 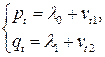
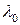
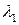
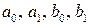
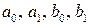

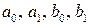
Рассмотрим эту же модель «спрос – предложение». Добавим в функцию спроса экзогенные переменные: 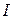
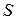
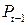
Воспользовавшись условием рыночного равновесия, можно преобразовать уравнения к системе приведенных уравнений 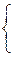

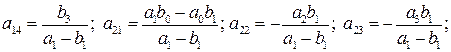
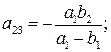
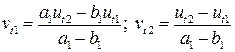
В системе (6.18), связывающей коэффициенты приведенных и структурных уравнений, восемь уравнений и семь коэффициентов 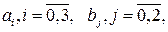
Для определения идентифицируемости структурных уравнений применяются необходимые и достаточные условия. Прежде чем их сформулировать введем следующие обозначения:
— 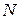
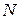
— 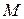
— 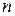
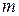
— 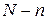
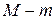
Первое необходимое условие. Уравнение идентифицируемо, если оно исключает, по крайней мере, 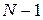
Второе необходимое условие. Уравнение идентифицируемо, если количество исключенных из уравнения экзогенных переменных не меньше количества эндогенных переменных в этом уравнении, уменьшенного на единицу:
Знаки равенства в необходимых условиях соответствуют точной идетификации уравнения.
Необходимое и достаточное условия идентифицируемости. В модели, содержащей 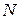
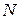
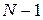
Рассмотрим применение данных условий для определения идентифицируемости структурных уравнений.
1.В модели «спрос – предложение»
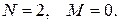
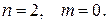
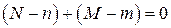
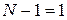

2.В модели 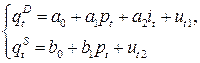
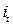

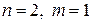
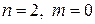
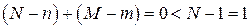
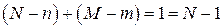
3. В модели 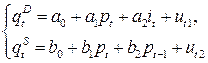
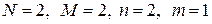
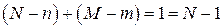
4.В модели 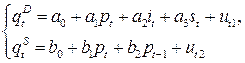
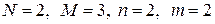
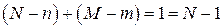
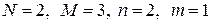
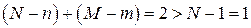
5.Оценим уравнения следующей структурной модели на идентифицируемость:
В данной модели три эндогенные переменные — 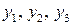
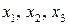
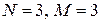
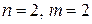
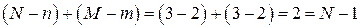
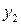
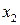
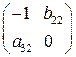
Ранг этой матрицы равен 2 ( 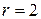
Для второго уравнения 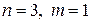
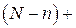
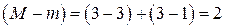
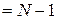
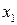
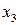
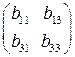
Ранг этой матрицы равен 2, следовательно, выполняется достаточное условие идентифицируемости, что подтверждает точную идентифицируемость уравнения.
Для третьего уравнения выполняется равенство 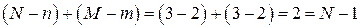
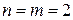
равен 2, что определяет точную идентифицируемость уравнения.
6.3. Методы оценивания параметров структурной модели. Косвенный метод наименьших квадратов. Двухшаговый метод наименьших квадратов. Раньше отмечалось, что если выполняются предпосылки применения МНК, то оценки параметров функции регрессии являются несмещенными, эффективными и состоятельными. МНК применяется и для оценки параметров некоторых структурных коэффициентов. Так, например, применение МНК для оценки структурных коэффициентов рекурсивной модели дает состоятельные оценки при соблюдении определенной последовательности действий. Сначала оцениваются параметры первого уравнения, в правой части которого содержатся только предопределенные переменные, т. е. эндогенная переменная 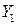
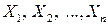
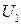
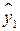
Метод наименьших квадратов не может применяться к оценке параметров структурных уравнений, так как они не учитывают одновременных соотношений между совместно зависимыми переменными. Поскольку в результате непосредственного применения МНК для каждого из уравнений модели получаем смещенные и несостоятельные оценки параметров, то разработан косвенный метод наименьших квадратов получения оценок, основанный на использовании приведенных уравнений.
Рассмотрим применение этого метода для кейнсианской модели формирования доходов (6.4) – (6.5). В приведенной форме эта модель выражается в виде двух уравнений (6.15) – (6.16):




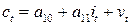

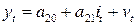
где 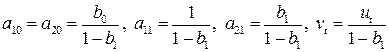
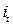
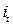
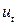
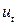
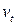
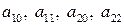
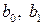
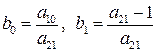
Определение оценок посредством преобразований уравнений к приведенной форме называется косвенным методом наименьших квадратов (КМНК).
Оценки, полученные по КМНК, являются состоятельными и они получаются однозначно, а соответствующее уравнение называется идентифицируемым (однозначно определенным).
Устранить коррелированность эндогенных переменных со случайным отклонением можно при помощи введения инструментальной переменной (ИП) 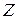
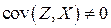
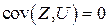
Так в структурном уравнении функции потребления (6.4) модели Кейнса, в качестве инструментальной переменной для 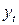
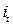
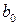
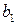
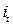
Рассмотрим еще один метод оценивания параметров, который учитывает многосторонние связи совместно зависимых переменных – двухшаговый метод наименьших квадратов (ДМНК). Суть этого метода состоит в поэтапном применении обычного метода наименьших квадратов для оценивания параметров структурного уравнения. Он применяется для нахождения инструментальной переменной, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные. На первом шаге ДМНК оценивается переопределенная переменная, опираясь лишь на экзогенные переменные. На втором этапе подставляем полученную оценку переопределенной переменной в исходную модель и получаем систему приведенных уравнений, для оценки параметров которой (приведенной системы) применяем МНК. В результате получаем состоятельные оценки структурных коэффициентов. При наличии в модели более одной переопределенной переменной на первом этапе необходимо оценить все такие переменные, выразив их через экзогенные и предопределенные переменные.
Пример 6.1.Рассмотрим эмпирические данные, характеризующие ВНП ( 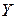
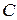
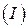
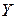 |
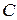 |
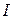 |
Предположим, что изучается закрытая экономика без государственных расходов, описываемая кейнсианской моделью:
Оценим параметры 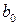
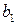
Р е ш е н и е. В п. 6.2 было показано, что модель Кейнса идентифицируема (количество уравнений, связывающих коэффициенты, равно количеству коэффициентов). Применив МНК для оценки параметров 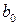
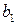
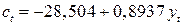
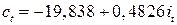
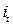
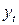
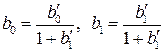
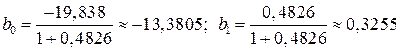
которые являются несмещенными и состоятельными оценками. Следовательно, кейнсианская модель имеет вид:
Литература
1. Болш Б., Хуан K.Дж. Многомерные статистические методы для экономики. M.: Статистика, 1979.
2. Булдык Г.M. Теория вероятностей и математическая статистика. Mн.: Выш. шк, 1989.
3. Булдык Г.М. Статистическое моделирование и прогнозирование: Учебник. – Мн.: НО ООО «БИП-С», — 2003.
4. Венецкий И.Г., Венецкая В.И. Основные математические понятия и формулы в экономическом анализе. M.: Статистика, — 1974.
5. Гренджер K., Хатанака M. Спектральный анализ временных рядов в экономике. M.: Мир, 1973.
6. Демиденко E.З. Линейная и нелинейная регрессия. M.: Финансы и статистика, 1981.
7. Джонсон Дж. Эконометрические методы. M.: Статистика, 1980.
8. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. M.: Статистика, 1973.
9. Имитационное и статистическое моделирование. / Ю.С.Харин, В.И. Малюгин, В.П.Кирилица и др. Mн.: Университетское, 1992.
10. Казинец Л.С. Темпы роста и структурные сдвиги в экономке. M.: Экономика, 1981.
11. Казмер Л. Методы статистического анализа в экономке. M.: Статистика, 1972.
12. Кендалл M.Дж. Временные ряды. M.: Финансы и статистика, 1981.
13. Кендалл M.Дж., Стюарт A. Многомерный статистический анализ и временные ряды. — M.: Наука, 1976.
14. Кильдешев Г.С., Френкель A.A. Анализ временных рядов и прогнозирование. M.: Статистика, 1973.
15. Максимей И.В. Математическое моделирование больших систем. Mн.: Выш. шк., 1985.
16. Персан M. Слейтер A. Динамическая регрессия: Теория и алгоритмы. M.: Финансы и статистика, 1984.
17. Сиськов В.И. Корреляционный анализ в экономических исследованиях. M.: Статистика, 1975.
18. Тейл Г. Прикладное экономическое прогнозирование. M.: Прогресс, 1970.
19. Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа. M.: Финансы и статистика, 1990.
20. Четыркин E.M. Статистические методы прогнозирования. M.: Статистика, 1977.
Содержание
В.1. Основные понятия и принципы моделирования социально- экономических систем……………………………………….
В.2. Классификация математических методов и моделей……. 8
В.3. Этапы построения математических моделей……………….12
1. Парная регрессия и корреляция……………………………….13
1.1.Понятие о функциональной, статистической и
корреляционной зависимостях ……………………………..13
1.2. Основные задачи прикладного корреляционно-
регрессионного анализа…………………………………… 16
1.3. Выбор формы однофакторной регрессионной модели……..18
1.4. Основные предпосылки применения метода наименьших
квадратов в аппроксимации связей признаков социально-
экономических явлений (условия Гаусса – Маркова)…… 17
1.5. Построение регрессионной прямой методом наименьших
1.6. Измерение интенсивности линейной корреляционной
1.7. Нелинейная регрессия и корреляция………………………..26
1.8. Проверка существенности оценок параметров
регрессии, коэффициентов корреляции и детерминации….31
1.9. Оценка адекватности регрессионной модели………………35
1.10. Пример построения однофакторной регрессионной
2. Многофакторные регрессионные модели…………….. 42
2.1. Построение многофакторной линейной регрессионной
2.2. Многофакторная линейная регрессионная модель в
2.3. Линейная частная регрессия…………………………………47
2.4.Отбор важнейших факторов многофакторных
2.5. Измерение интенсивности множественной связи…………. 50
2.6. Проверка статистической существенности (значимости)
параметров множественной регрессии и показателей
интенсивности корреляционной связи……………………. 57
2.7. Проверка выполнимости предпосылок МНК.
Статистика Дарбина – Уотсона…………………………….. 63
2.8. Оценка адекватности многофакторной регрессионной
2.9. Построение многофакторной регрессионной модели…… 66
3. Прогнозирование взаимосвязей экономических
явлений на основе факторных регрессионных моделей…71
4. Эконометрический анализ при нарушении классических модельных предположений…………………………………. 78
4.1. Гетероскедастичность. Критерии Парка и Голдфелда –
Квандта для обнаружения гетероскедастичности…………….78
4.2. Методы смягчения проблемы гетероскедастичности………. 81
4.3. Автокорреляция остатков регрессионной модели.
Критерий Дарбина – Уотсона…………………………………..83
4.4. Мультиколлинеарность экзогенных переменных.
Методы устранения мультиколлинеарности…………………..86
5.Модели с дихотомическими (фиктивными) переменными.89
5.1. Необходимость использования фиктивных переменных……. 89
5.2. Регрессионные модели с количественными и
качественными переменными………………………………… ..89
5.3. Модели с фиктивными результативными признаками………. 92
6. Системы эконометрических уравнений……………………94
6.1. Системы уравнений используемых в эконометрике…………..94
6.2. Проблема идентифицируемости модели. Необходимое
и достаточное условие идентифицируемости…………………98
6.3. Методы оценивания параметров структурной модели.
Косвенный метод наименьших квадратов.
Двухшаговый метод наименьших квадратов………………….102
, Громов : для экономических специальностей
-*наука, которая дает количественное выражение взаимосвязей в экономике;
-учение о системе показателей, дающих представление об экономике;
-различного рода цифровые данные.
2. Предметом эконометрики является:
-*определение наблюдаемых в экономике количественных закономерностей;
-сбор цифровых данных;
3. К одному из методов эконометрики относится:
-счета и двойная запись;
4. Эконометрическая модель описывает:
-*стохастические связи между переменными;
-функциональные связи между переменными;
-набор цифровых данных;
5. Переменные, определяемые из уравнений модели, называются:
6. Переменные, задаваемые «из вне», в определенной степени управляемые (планируемые), называются:
7. Переменные, задаваемые «из вне», в определенной степени управляемые (планируемые), называются:
-предопределенные.
8. Пространственные данные фиксируются:
-*в один и тот же момент времени по нескольким объектам;
-по одному объекту за период времени.
-по нескольким объектам за период времени.
9. Идентификация модели – это:
-*статистическое оценивание неизвестных параметров модели;
-формулировка вида модели, состава и формы входящих в нее связей;
-сбор необходимой статистической информации;
-статистическое оценивание неизвестных параметров модели;
-проверка точности модельных данных.
10. Верификация модели – это:
-*проверка точности модельных данных.
-статистическое оценивание неизвестных параметров модели;
-формулировка вида модели, состава и формы входящих в нее связей;
-сбор необходимой статистической информации;
-статистическое оценивание неизвестных параметров модели
11. Статистическими называются выводы, полученные путем:
-*обобщения свойств выборки на генеральную совокупность;
-измерения генеральной совокупности;
-сбора статистических данных.
12. Выборочное среднее является;
-*оценкой среднего в генеральной совокупности;
-наиболее часто встречающейся величиной в генеральной совокупности;
-оценкой разброса в генеральной совокупности.
13. Выборочное среднее квадратическое отклонение является:
-*оценкой разброса в генеральной совокупности.
-оценкой среднего в генеральной совокупности;
-наиболее часто встречающейся величиной в генеральной совокупности.
14. Выборочный коэффициент корреляции является:
-*оценкой относительной меры разброса в генеральной совокупности;
-оценкой среднего в генеральной совокупности;
-наиболее часто встречающейся величиной в генеральной совокупности;
15. Если коэффициент корреляции между двумя случайными величинами больше нуля, то значит:
-*случайные величины имеют прямую линейную зависимость;
-случайные величины имеют обратную линейную зависимость;
-случайные величины не зависимы.
16. Если коэффициент корреляции между двумя случайными величинами меньше нуля, то значит:
-*случайные величины имеют обратную линейную зависимость;
-случайные величины имеют прямую линейную зависимость;
-случайные величины не зависимы.
17. Нулевой называется:
-*гипотеза, подвергающаяся проверке;
-гипотеза, которая отклоняется;
-гипотеза, которая содержит одно конкретное предположение.
18. Альтернативной называется:
-*гипотеза, необходимая для проверки нулевой гипотезы;
-гипотеза, которая отклоняется;
-гипотеза, которая содержит несколько конкретных предположений.
19. Уровнем значимости называется:
-*вероятность отвергнуть правильную нулевую гипотезу;
-совокупность значений критерия проверки, при которых нулевую гипотезу отклоняют;
-совокупность значений критерия проверки, при которых нулевую гипотезу не отклоняют.
20. Случайным называется такое событие, которое:
-*может произойти или не произойти в условиях данного эксперимента;
-не происходит никогда в условиях данного эксперимента;
-происходит всегда в условиях данного эксперимента.
21. Достоверным называется такое событие, которое:
-*происходит всегда в условиях данного эксперимента;
-может произойти или не произойти в условиях данного эксперимента;
-не происходит никогда в условиях данного эксперимента;
22. Невозможным называется такое событие, которое:
-*не происходит никогда в условиях данного эксперимента
-может произойти или не произойти в условиях данного эксперимента;
-происходит всегда в условиях данного эксперимента
23. К несовместимым относятся события, которые:
-*не могут происходить одновременно;
-характеризуются тем, что одно из них происходит тогда и только тогда, когда не происходит другое.
24. Вероятность события А изменяется в пределах:
-*
—
—
25. Для вероятности достоверного события характерно:
-* 
—
—
26. Для вероятности невозможного события характерно:
-*
—
—
27. Для вероятности несовместимых событий характерно:
. Для вероятности противоположных событий характерно:
29. Случайной величина:
-*заранее не известное численное значение, зависящее от случайных обстоятельств;
-количественная мера для сравнения событий по степени возможности их появления;
-исход или совокупность исходов вероятностного эксперимента.
30. Законом распределения дискретной случайной величины называется:
-*соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями;
-функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х;
-функция, производная от функции распределения дискретной случайной величины.
31. Функцией распределения случайной величины Х называется:
-*функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х;
-соответствие между всеми возможными значениями случайной величины и их вероятностями;
-функция, производная от функции распределения непрерывной случайной величины.
32. Плотностью распределения вероятностей случайной величины Х называется:
-*функция, производная от функции распределения случайной величины
-соответствие между всеми возможными значениями случайной величины и их вероятностями;
-функция, определяющая вероятность того, что случайная величина X примет значение, меньшее, чем Х
33. Плотность распределения вероятностей можно записать:
-*для непрерывных случайных величин;
-для дискретных случайных величин;
-для любых случайных величин.
34. К числовым характеристикам положения случайной величины относится:
-среднее квадратическое отклонение
35. К числовым характеристикам рассеивания (разброса) случайной величины относится:
36. Математическое ожидание характеризует:
-*среднее ожидаемое значение случайной величины;
-наиболее часто встречающееся значение случайной величины;
-серединное значение ряда упорядоченных случайных величин.
37. Стандартизированное нормальное распределение имеет параметры:
-*
—
—
38. Какими параметрами определяется распределение Фишера?
-*числами степеней свободы m и n
-числом степеней свободы n
-числом степеней свободы n-m
39. Если случайные величины X и Y независимы, то
-*
—
—
40. Примером дискретной случайной величины является:
-*списочное число работников предприятия
-выручка от реализации за текущий месяц
-прибыль от реализации за текущий месяц
41. Примером непрерывной случайной величины является:
-тарифный разряд работников предприятия
-количество станков в цехах
42. При увеличении уровня доверительной вероятности ширина доверительного интервала:
43. В экономике чаще всего большинство случайных величин задается в виде:
-закрытых случайных величин;
-*непрерывных случайных величин;
-закрытых случайных величин и непрерывных случайных величин
44. К какому закону распределения можно отнести показатели дохода населения, прибыли фирм в отрасли, объема потребления?
-закон распределения Хи – квадрат;
-закон распределения Стьюдента;
-закон распределения Фишера;.
-*нормальный закон распределения (распределение Гаусса).
45. Законы распределения случайной величины необходимы для:
-определения интервальных оценок;
-проверки статистических гипотез;
-*определения интервальных оценок и проверки статистических гипотез.
46. Квантиль определяется:
-числом степеней свободы;
-*уровнем значимости и числом степеней свободы.
47. Какие из перечисленных числовых характеристик используются для анализа степени взаимосвязи случайных величин?
-*ковариация и коэффициент корреляции;
-вероятность и коэффициент корреляции.
48. Ковариация является:
-*абсолютной мерой взаимосвязи;
-относительной мерой взаимосвязи;
-относительной частотой взаимосвязи.
49. Коэффициент корреляции является величиной:
-имеет ту же единицу измерения, что и случайная величина.
Системы эконометрических уравнений
Эконометрика как учебная дисциплина на современном этапе благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов является одним из базовых курсов в системе высшего экономического образования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Эконометрика
Эконометрика — это статистико-математический анализ экономических отношений.
Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, спроса-предложения в данное время в данном месте и т.д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам.
Виды систем эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений, применяемых в эконометрике:
• система независимых уравнений — когда каждая зависимая переменная 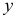
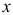
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;
• система рекурсивных уравнений — когда зависимая переменная 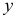
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности;
• система взаимосвязанных (совместных) уравнений — когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:
Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.
Возможно эта страница вам будет полезна:
Введем следующие определения:
- Эндогенные переменные — взаимозависимые переменные, которые определяются внутри системы (модели)
.
- Экзогенные переменные — независимые переменные, которые определяются вне системы
.
- Лаговые эндогенные переменные — эндогенные переменные за предыдущие моменты времени.
- Предопределенные переменные — экзогенные и лаговые эндогенные переменные системы.
- Коэффициенты
и
при переменных — структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы — приведенная форма модели:
где 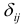
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация -это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
- идентифицируемые;
- неидентифицируемые;
- сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель еверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.
Сверхидентифицируемая модель, в отличие от неидентифицируемой, модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Обозначим через 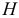
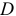
- уравнение идентифицируемо, если
;
- уравнение сверхидентифицируемо, если
;
- уравнение неидентифицируемо, если
.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных -двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
• обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Решение эконометрических уравнений
Пример задачи с уравнением №4.2.1.
Рассматривается модель протекционизма Сальватора (упрощенная версия):
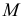
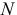
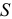
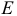
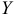
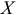
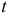
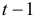
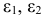
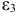
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 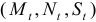
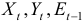
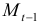
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает три эндогенные переменные 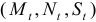
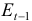
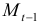
Это уравнение включает три эндогенные переменные 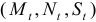
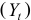
Это уравнение включает три эндогенные переменные 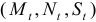
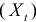
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо. 2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
так как она содержит отличный от нуля минор второго порядка
Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо. 3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы 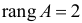
Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
- Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
Пример задачи с уравнением №4.2.2.
Рассматривается структурная модель вида:
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
- Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 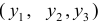
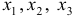
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 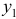
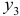
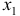
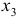
Это уравнение включает три эндогенные переменные 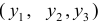
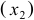
Это уравнение включает две эндогенные переменные (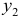
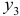
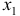
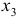
Для этого составим матрицу коэффициентов при переменных модели:
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
- Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
- Вычисление структурных коэффициентов модели:
1) из третьего уравнения приведенной формы выразим 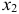
Данное выражение содержит переменные 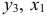
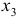
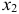
Откуда получим первое уравнение СФМ в виде
2) во втором уравнении СФМ нет переменных 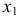

Первый этап: выразим 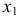
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 

Подставим его в выражение для
Второй этап: аналогично, чтобы выразить 
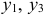
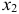

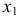
Подставим полученные 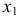

В результате получаем второе уравнение СФМ
3) из второго уравнения ПФМ выразим 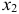
Подставим полученное выражение в третье уравнение ПФМ
В результате получаем третье уравнение СФМ
Таким образом, СФМ примет вид
Пример задачи с уравнением №4.2.3.
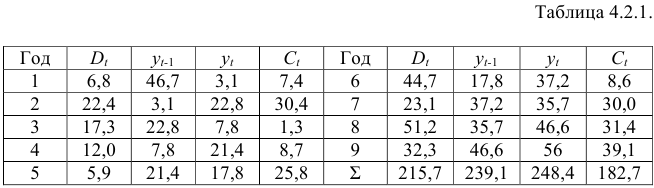
Изучается модель вида
где 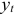
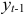
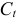
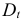
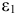
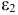
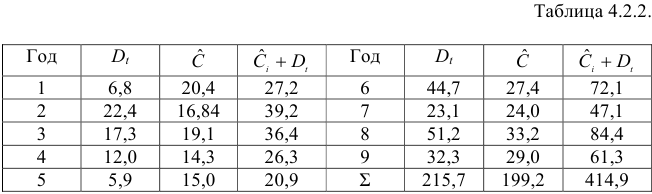
Информация за девять лет о приросте всех показателей дана в таблице 4.2.1.
Для данной модели была получена система приведенных уравнений
- Применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели.
- Рассчитать параметры первого уравнения структурной модели.
Решение:
- В данной модели две эндогенные переменные (
и
) и две экзогенные переменные (
и
). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при 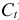
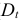
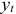
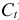
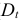
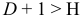
- Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 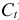
подставим значения 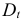
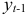
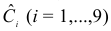
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 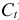
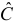
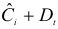
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 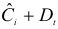
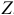
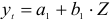
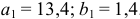
Пример задачи с уравнением №4.2.4.
Рассматривается следующая модель:
— расходы на потребление в период
;
— совокупный доход период
:
— инвестиции в период
;
— процентная ставка в период
;
— денежная масса в период
;
— государственные расходы в период
;
— расходы на потребление в период
;
— инвестиции в период
;
— текущий период;
— предыдущий период;
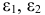
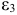
В предположении, что имеются временные ряды данных по всем переменным модели, предложить способ оценки ее параметров.
Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
Решение:
- Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 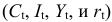
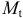
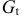
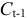
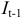
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 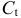
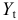
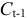
Это уравнение включает две эндогенные переменные 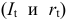
3-е уравнение тоже включает две эндогенные переменные 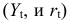
Это уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее числа эндогенных переменных модели минус 1, т. е. 4-1=3.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 1-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 2-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен трем, так как имеется квадратная подматрица 3×3 этой матрицы, определитель которой не равен нулю.
Достаточное условие идентификации для 3-го уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК.
Шаг 1. Запишем приведенную форму модели в общем виде
где 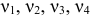
Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчётные значения эндогенных переменных 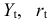
Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями
Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная 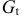
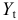
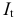
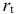
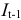
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://pandia.ru/text/77/489/6991.php
http://lfirmal.com/sistemy-ekonometricheskih-uravneniy/
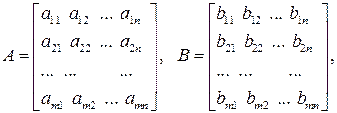
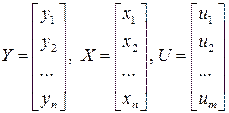
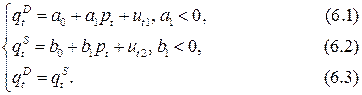

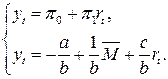
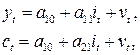
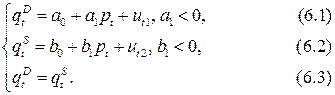
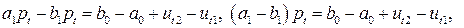
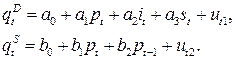
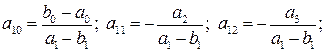
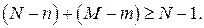
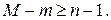
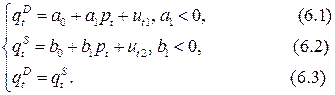
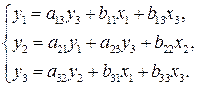
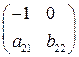
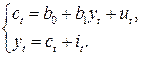
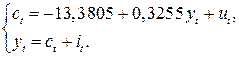



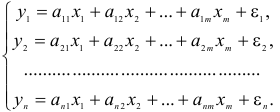
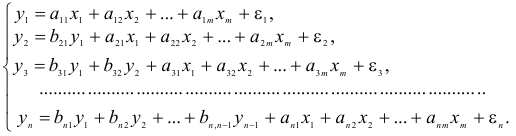
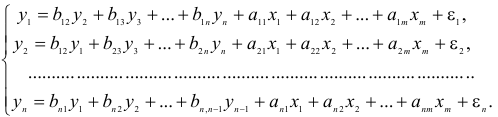
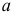 и
и 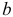 при переменных — структурные коэффициенты модели.
при переменных — структурные коэффициенты модели.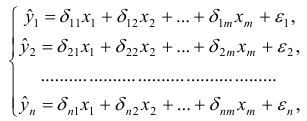
 ;
; ;
;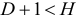 .
.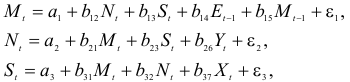

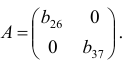
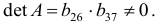
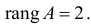
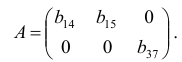
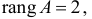
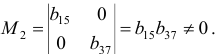
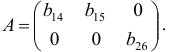
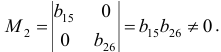
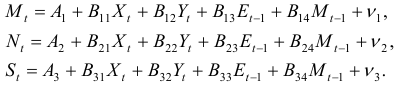
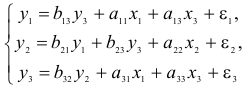
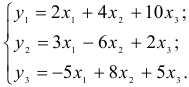

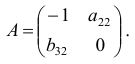
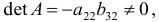
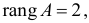
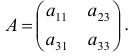
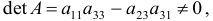
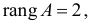
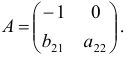
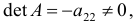
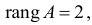
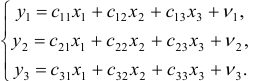
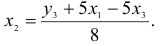
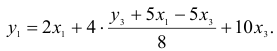
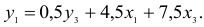
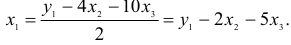
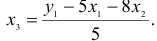
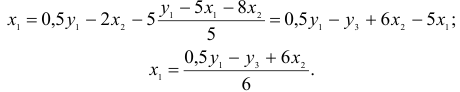
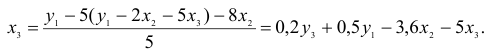
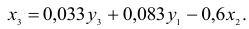
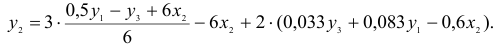
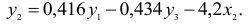
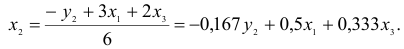
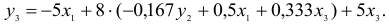
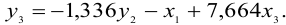
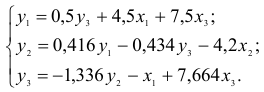
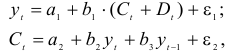
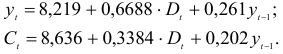
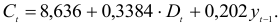
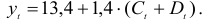
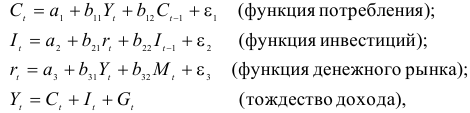
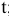 ;
;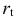 — процентная ставка в период
— процентная ставка в период 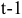 ;
;