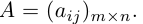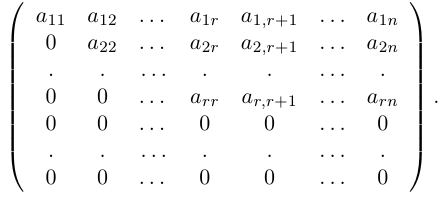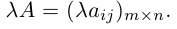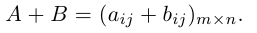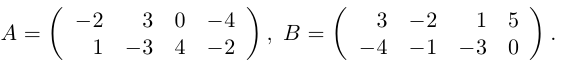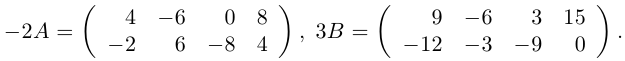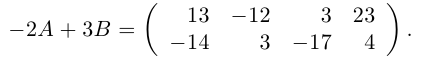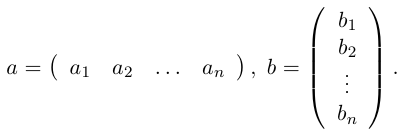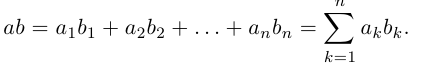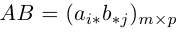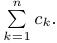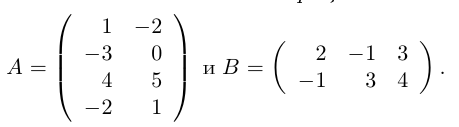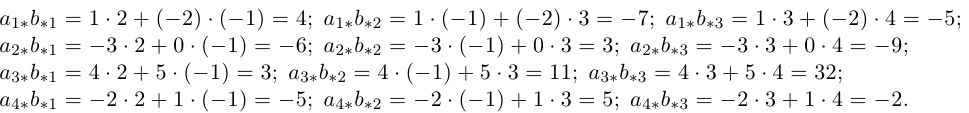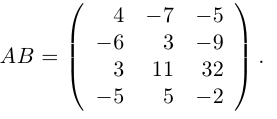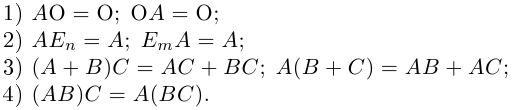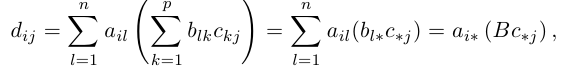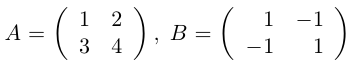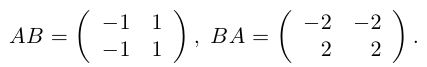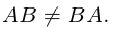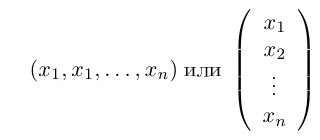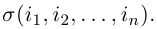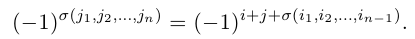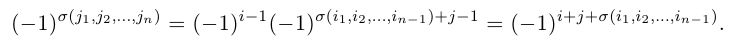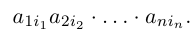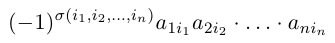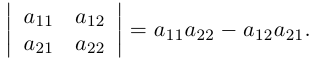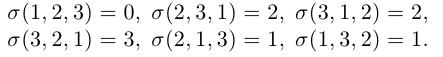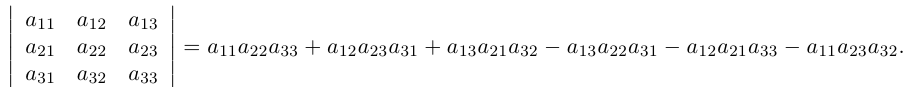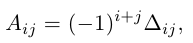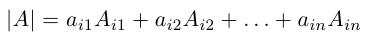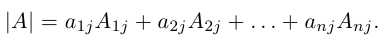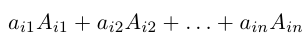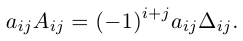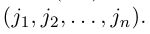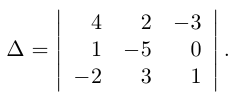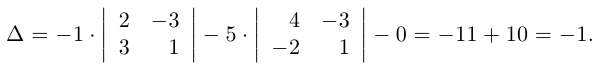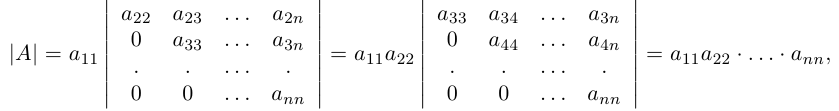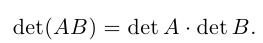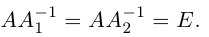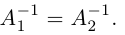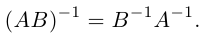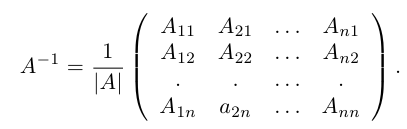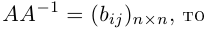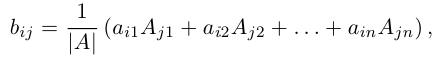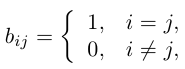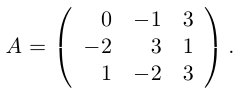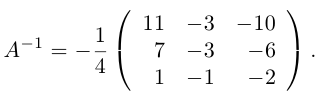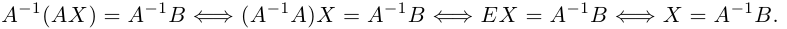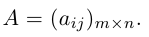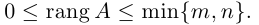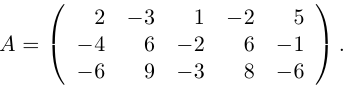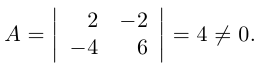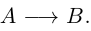Перестановка чисел в линейных уравнениях

05. Перестановки и подстановки

Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т. е.

=

= (7)

Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки.

Пусть дан упорядоченный набор из N элементов. Элементы этого набора занумеруем числами 1, 2, 3, … , n. Очевидно, вместо того, чтобы говорить об элементах, можно говорить об их номерах.

Определение 5. Перестановкой Из N Чисел (или N символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений).

Теорема 1. Число перестановок из N Символов равно n!

Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1 ) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2 ) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами.

Говорят, что числа К и Р образуют в перестановке (…К…р…) Инверсию, если К > Р, Но в перестановке К стоит раньше Р. Перестановка называется Чётной, если она содержит чётное число инверсий. Перестановка называется Нечётной, если она содержит нечётное число инверсий.

Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий.

2) Перестановка ( 2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий.

Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется Транспозицией.

Теорема 2. Всякая транспозиция меняет чётность перестановки.

Доказательство. Пусть в перестановке символы К и Р меняются местами. При этом возможны два случая.

1) Символы К и Р В данной перестановке стоят рядом, т. е. (…К, Р …). После транспозиции получится перестановка (….Р, к …). Если К и Р Составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые К и Р Составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т. е. чётность перестановки изменится.

2) Символы К и Р В данной перестановке стоят не рядом, т. е. (….К,…,р…). После транспозиции получится перестановка (…Р,…,к…). Число инверсий, которые К и Р Составляли в данной перестановке с символами, стоящими перед К И после Р, не изменится. Если между К и Р Стоят M символов, то переставить К и Р можно следующим образом: переставить К последовательно с каждым из этих M Символов, затем переставить К и Р, затем в обратном порядке переставить Р с каждым из этих M символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась.

Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!.

Определение 6. Подстановкой из N символов ( или Подстановкой N-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя.

Элементы данного множества будем обозначать 1, 2, …, n. Подстановка А может быть записана так: если число К переходит в число aК, то А = . Если в записи подстановки А Некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т. е. та же подстановка. Например,

А = = .

Запись подстановки А = будем называть стандартной. Всякую подстановку можно записать в стандартном виде. Верхнюю и нижнюю строки подстановки можно рассматривать как перестановки. Подстановка А называется чётной, если её верхняя и нижняя строки есть перестановки одинаковой чётности, т. е. общее число инверсий в них – чётное. В противном случае А Называется Нечётной. Так как перестановка столбцов равносильна транспозиции как в верхней так и в нижней строке, то при перестановке столбцов чётность подстановки не изменится, поэтому чётность подстановки можно вычислять по её стандартному виду и в этом случае она совпадает с чётностью нижней строки.

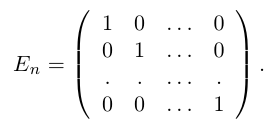
Подстановка Е = называется Тождественной Или Единичной.

Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А = , В = , то

А×В = . Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично, , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, .

Аналогично получаем, что В×А = . Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В)×С = А×(В×С) для любых подстановок А, В, С Одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, Если А и Е Одного порядка. Для подстановок А = и В = очевидно А×В = В×А = Е. Следовательно, А-1 = В, т. е. каждая подстановка имеет обратную.

Линейная алгебра — примеры с решением заданий и выполнением задач

Содержание:

Линейная алгебра

Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.

Матрицы и операции над ними

В математике и ее приложениях наряду с числами часто бывает удобным использовать чис­ловые таблицы, которые называются матрицами. Аппарат теории матриц эффективно приме­няется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.

Определение: Матрицей размерности m х n называется прямоугольная таблица дейст­вительных чисел, состоящая из m строк и n столбцов.

Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам мат­рицы используются два индекса: первый указывает на номер строки, второй — на номер столб­ца, на пересечении которых расположен данный элемент.

Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:

Более компактно с указанием элементов матрица записывается в виде:

Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.

Рассмотрим некоторые специальные виды матриц.

Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.

Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.

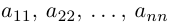
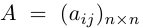
Числа в квадратной матрице называются диагональными элементами. Совокупность диагональных элементов составляет главную диагональ квадрат­ной матрицы.

Квадратная матрица, диагональные элементы которой равны единице, а все остальные — нулю, называется единичной матрицей и обозначается через 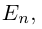где n — порядок матрицы.

Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица

Матрица называется трапециевидной, если она представляет собой следующую таблицу:

Операции над матрицами

Введем сначала линейные операции над матрицами.

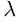
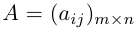
Произведением действительного числа на матрицу называется матрица

Суммой двух матриц 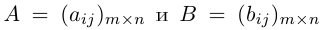одинаковой размерности называется матрица

Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.

Разность матриц А и B можно определить как А — В = А + (-1)В.

Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.

Пример №1

Найти матрицу -2А +3В.

Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.

Произведением этих строки и столбца называется число1

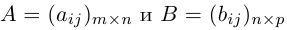
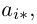
Рассмотрим так называемые согласованные матрицы , у первой из которых число столбцов равно числу строк второй матрицы. Обозначим строку с номером i матрицы А через а столбец с номером j матрицы B через

Произведением данных согласованных матриц А и B называется матрица

Часто для суммы n чисел 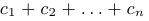мы будем использовать короткое обо значение

размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.

Пример №2

Найти произведение согласованных матриц

Решение. Найдем произведение строк матрицы А на столбцы матрицы В.

Осталось записать искомое произведение матриц:

Отметим некоторые свойства произведения матриц1.

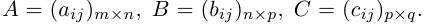
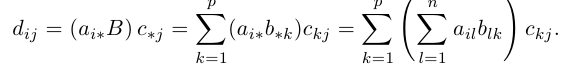
Первые три сразу следуют из определения произведения матриц. Докажем последнее свой­ство. Пусть заданы три матрицы Элемент dij произ­ведения (AB)C равен произведению строки с номером i матрицы AB на столбец с номером j матрицы C : Поменяв порядок суммирования в последней двойной сумме, получим:

что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.

Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не переста­новочны). Приведем соответствующий

Контрпример. Доказать, что матрицы

Таким образом, для этих матриц

Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.

Мы предполагаем, что все матрицы в свойствах согласованы.

Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.

Определитель матрицы и его свойства

Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Вве­дем предварительно понятие перестановки и изучим некоторые ее свойства.

Перестановки

Перестановкой n натуральных чисел 1, 2, . n называется строка

(1)

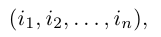
содержащая все эти числа.

Первым элементом перестановки может быть любое из чисел 1, 2, . n, вторым — любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно (читается n-факториал).

Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через

В связи с этим перестановка (1) называется четной, если в ней число 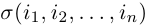четно и нечетной — в противном случае.

Отметим два свойства перестановок, которые мы будем использовать ниже.

Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.

Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или на­столько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем пере­ставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четно­сти исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.

Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных переста­новок, мы получим p нечетных и, следовательно, где q — количество нечетных перестано­вок. Аналогично мы можем убедиться в справедливости неравенства Из этих неравенств и следует, что p = q.

Лемма 2. Пусть

(2)

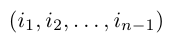
— перестановка чисел 1, 2, . n — 1. Зафиксируем число j из множества <1, 2, . , n>и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, . , n — 1 и увеличив на единицу все не меньшие, чем j элемен­ты этой перестановки. В результате получим перестановку

(3)

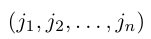
чисел 1, 2, . , n. Четности перестановок (2) и (3) связаны равенством

Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 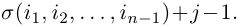Перегоним теперь число j на место с номером i, последовательно обменивая его со следующими i — 1 элементами. По лемме 1 характер четности перестановки изменится i — 1 ра и, значит,

Определитель и его вычисление для матриц второго и третьего порядков

Рассмотрим квадратную матрицу порядка n :

Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:

Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, . , n.

Определение: Число, равное сумме всех n! произведений

называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как

Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.

Так как 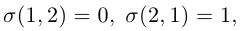то

Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :

Тогда

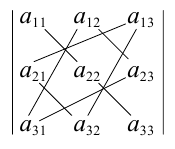
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком » + » следует брать произведения по схеме

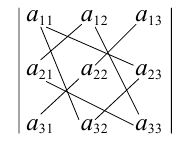
а со знаком » — » — по схеме

Пример №3

Решение. Воспользуемся правилом треугольников: = —2 + 6 — 6 — 9 — 8 — 1 = -20.

Свойства определителя

1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.

2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.

3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указан­ной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.

Эти свойства напрямую следуют из определения определителя.

4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.

Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.

5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.

В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесе­ния за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.

6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) доба­вить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.

Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.

Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополне­ния к элементу матрицы.

Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число

где 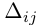— определитель порядка n — 1, полученный из определителя этой матрицы вычеркиванием i-ой строки и j-го столбца.

7) Разложение определителя по элементам строки (столбца).

Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столб­ца) на соответствующие алгебраические дополнения. Таким образом,

Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение

содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.

Рассмотрим произвольное произведение

Каждое слагаемое определителя 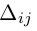представляет собой произведение элементов данной мат­рицы, взятых по одному из каждой строки и каждого столбца, исключая строку с номером i и столбец с номером j. Знак этого произведения определяется четностью перестановки

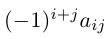
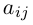
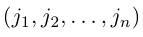
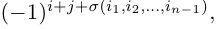
чисел 1, 2, . , n — 1. Умножив данное произведение на число и поставив множитель на место с номером i, мы получим соответствующее произведение определителя матрицы А с перестановкой вторых индексов и знаком который по лемме 2 пункта 1 соответствует четности перестановки

Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.

Пример №4

Решение. Разложим этот определитель по элементам второй строки:

Пример №5

Вычислить определитель треугольной матрицы

Разлагая этот и следующие определители по первому столбцу, получим:

таким образом, определитель треугольной матрицы равен произведению диагональных эле­ментов.

8) Сумма произведений n действительных чисел на алгебраические дополнения к элементам какой-нибудь строки (столбца) равна определителю, в котором в указанной строке (столбце) расположены данные числа, а все остальные элементы совпадают с соответствующими элементами исходного определителя.

Это свойство является прямым следствием предыдущего.

9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические до­полнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.

Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.

10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.

Достаточно громоздкое доказательство этого свойства мы приводить не будем.

Обратная матрица

Определение: Обратной к квадратной матрице 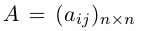называется обозначаемая через А-1 матрицы, для которой АА-1 = А-1А = Е, где Е — единичная матрица.

Из этого определения следует, что матрица А-1 также является квадратной той же размер­ности, что и матрица А.

Отметим некоторые свойства обратной матрицы, следующие из ее определения.

а) У матрицы не может существовать больше одной обратной.

Действительно, пусть для матрицы А имеются две обратные 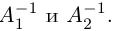Тогда

Умножив обе части первого равенства слева на матрицу получим

c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем

Выясним условия, при которых обратная матрица существует.

Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.

Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А det А-1 = det E = 1. Следователь но, det А 0.

Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:

Действительно, если

откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:

т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.

В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.

Пример №6

Найти обратную к матрице

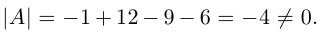
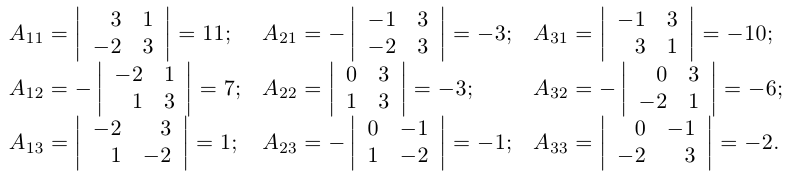
Решение. Найдем сначала определитель матрицы: Обратная матрица существует. Находим алгебраические дополнения к элементам данной матрицы:

Следовательно,

Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение

с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:

Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а ре­шением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.

Ранг матрицы и его вычисление

Рассмотрим произвольную матрицу

Минором порядка k матрицы A называется определитель, стоящий на пересечении выбран­ных k строк и k столбцов данной матрицы.

Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.

Естественно считать, что rang O = 0. Очевидно также, что

Пример №7

Найти ранг матрицы

Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:

Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.

Как видно из определения, вычисление ранга матрицы через миноры является весьма тру­доемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.

Элементарными преобразованиями матрицы называются следующие операции над ее стро­ками или столбцами:

1. перестановка двух строк (столбцов) матрицы;
2. умножение строки (столбца) на ненулевое действительное число;
3. добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.

Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как

Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.

Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. 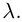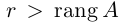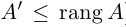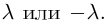Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число Возьмем в матрице А’ минор М порядка (если такого минора нет, то rang ). Этот минор либо совпадает с минором матрицы A, либо по свойствам 3). 2). 4) определителя он равен сумме двух миноров матрицы А с действительными коэффициентами, один из которых равен 1. а второй В обоих случаях по определению ранга матрицы минор М равен 0. Следовательно, rang А’ n.

Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.

Доказательство:

Достаточность: 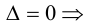система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Линейные уравнения. Решение линейных уравнений. Правило переноса слагаемого.

Правило переноса слагаемого.

При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения. Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус». Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный. Кроме того, правило работает и для неравенств.

Примеры переноса слагаемого:

Сначала переносим 5x из левой части уравнения в правую:

Далее переносим (−6) из правой части в левую:

Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+». При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение.

Переносим 1-е слагаемое в правую сторону уравнения. Получаем:

Обратите внимание, что в нашем примере слагаемое — это выражение (−3x 2 (2+7x)). Поэтому нельзя отдельно переносить (−3x 2 ) и (2+7x), так как это составляющие слагаемого. Именно поэтому не переносят (−3x 2 ⋅2) и (7x). Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга.

Таким же образом преобразовывают неравенства:

Собираем каждое число с одной стороны. Получаем:

2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону. Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-».

Это правило зачастую используется для решения линейных уравнений. Для решения систем линейных уравнений используются другие методы.