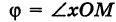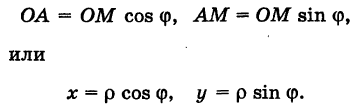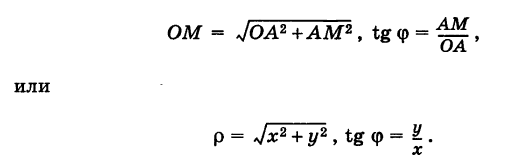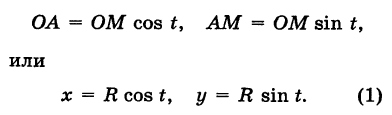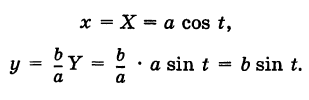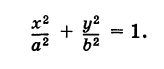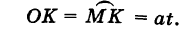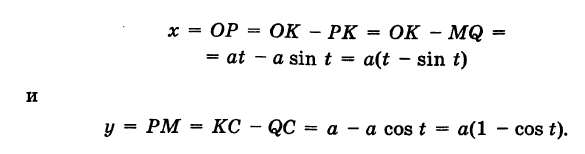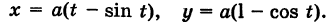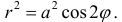Перевести уравнение кривых в полярные координаты

Перевести уравнение кривых в полярные координаты

Построим график функции в полярных координатах r=r(φ),
где 0 Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x ctg(x) Функция — Котангенс от x arcctg(x) Функция — Арккотангенс от x arcctgh(x) Функция — Гиперболический арккотангенс от x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

© Контрольная работа РУ — калькуляторы онлайн

Полярные координаты — определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

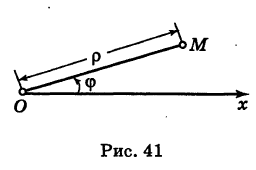
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

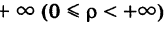
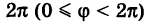
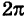
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

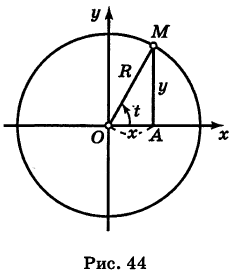
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

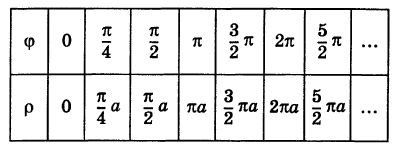
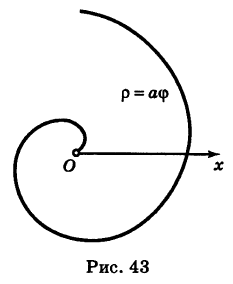
Рассмотрим кривую 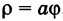, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты , рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М — произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

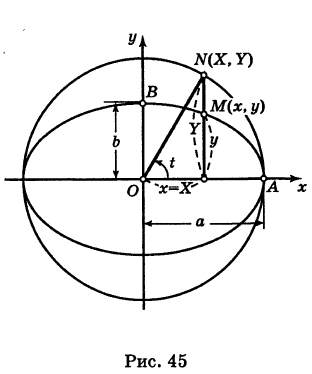
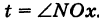
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

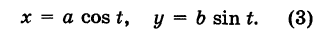
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

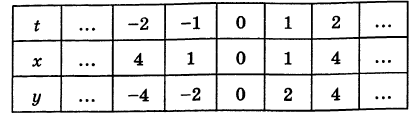
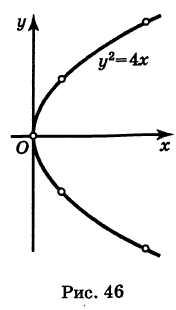
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 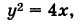т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

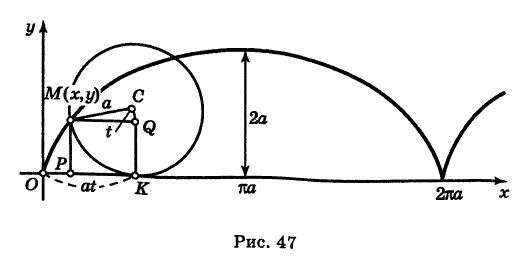
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

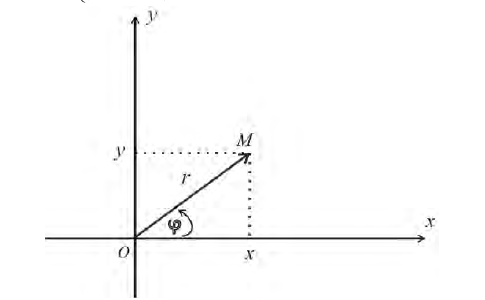
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 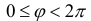. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 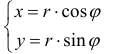(1)

Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
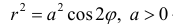
Решение.

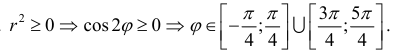
Вычислим значения r при различных значениях ϕ :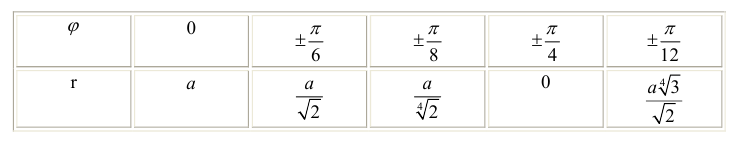

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

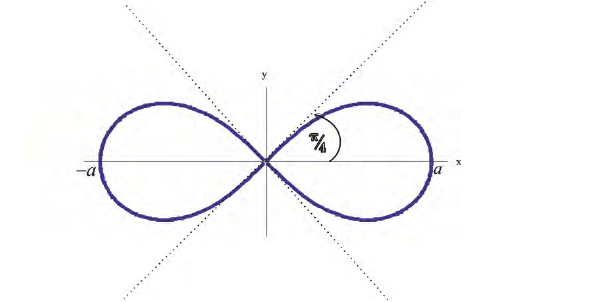
Рис.3. Лемниската

Пример 2.

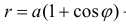
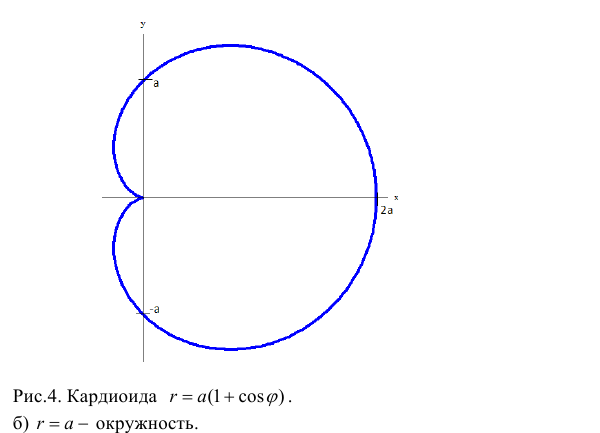
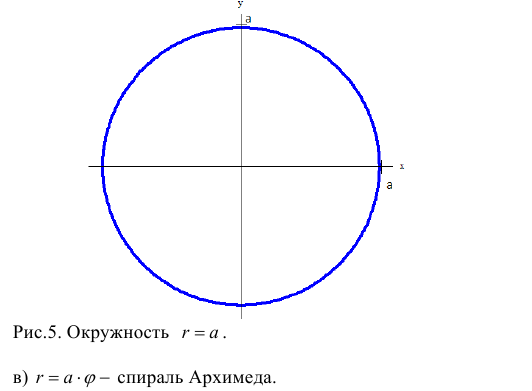
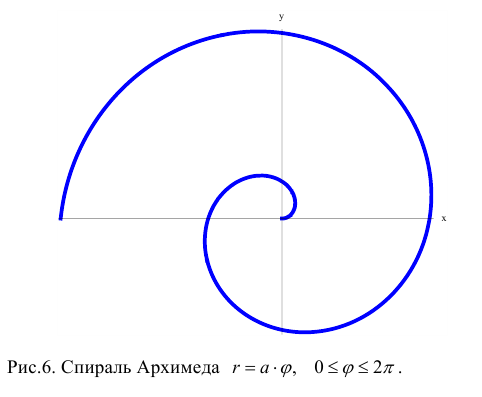
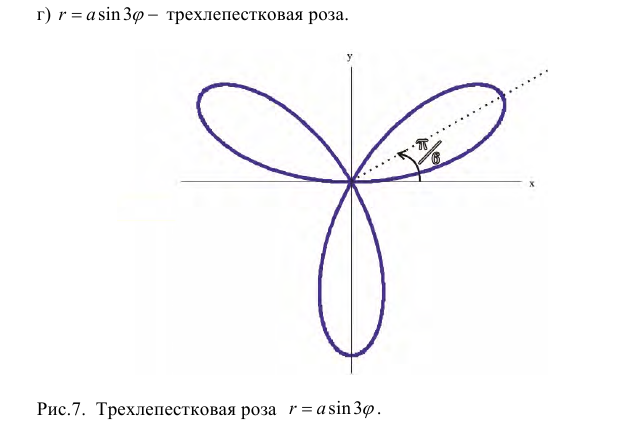
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

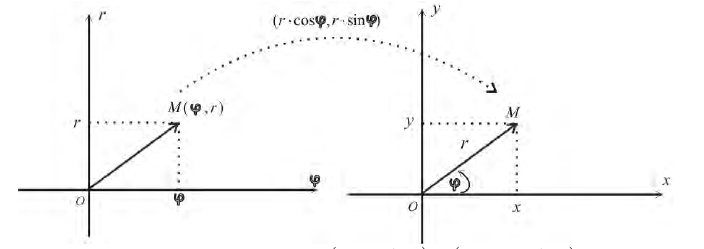
При этом, если r > 0, то векторы 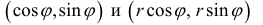сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Аналитическая геометрия
• Высшая математика.
• Аналитическая геометрия.
• Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Уравнение эллипса, гиперболы, параболы в полярной системе координат.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пример.

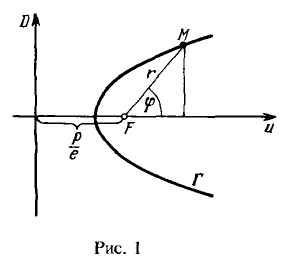
Пусть $\Gamma -$ эллипс, ветвь гиперболы или парабола, $F -$ фокус этой кривой, $D -$ соответствующая директриса. Вывести уравнение кривой $\Gamma$ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1).

Решение.

Общее свойство эллипса, гиперболы и параболы состоит в следующем $$M\in\Gamma\Leftrightarrow\frac<\rho(M, F)><\rho(M, D)>=const=e,\qquad\qquad (1)$$ где $e -$ эксцентриситет кривой ( $e 1$ для гиперболы и $e=1$ для параболы)

Обозначим расстояние от фокусы до директрисы через $\frac

$( $p-$ параметр кривой, называемый полуфокальным параметром). Тогда из рисунка 1 следует, что $\rho(M, F)=r$ и $\rho(M, D)=\frac

+r\cos\varphi.$ Подставляя эти выражения в (1), получаем $$\frac<\frac

+r\cos\varphi>=e,$$ откуда $$r=\frac

<1-e\cos\varphi>.\qquad\qquad (2)$$ Уравнение (2) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы.

Примеры.

2.321(а).

Для эллипса $\frac<25>+\frac<16>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в левом фокусе.

Решение.

Найдем эксцентриситет параболы и параметр $p:$

Далее, подставляя найденные параметры в полярное уравнение (2), найденное в предыдущей задаче, найдем уравнение данного эллипса:

2.324(а).

Написать каноническое уравнение кривой второго порядка $r=\frac<9><5-4\cos\varphi>.$

Решение.

Приведем заданное уравнение, к уравнению вида $r=\frac

<1-e\cos\varphi>:$

Отсюда имеем: $e=\frac<4><5>,$ $p=\frac<9><5>.$ Поскольку $e

Далее, подставляя выражения эксцентриситета и параметра по определению, надем полуоси эллипса:

Таким образом, запишем каноническое уравнение эллипса:

Вывести полярное уравнение гиперболы $\frac-\frac=1,$ при условии, что полярная ось сонаправлена с осью $Ox,$ а полюс находится в центре гиперболы.

Решение.

Так как полюс находится в центре гиперболы, то $OM=r,$ тогда $\rho(M, D)=r\cos\varphi-\frac,$ $\rho(M, F)=\sqrt <(r\sin\varphi)^2+(c-r\cos\varphi)^2>.$

Таким образом, из уравнения (1) находим:

Домашнее задание.

2.321(б) Для эллипса $\frac<25>+\frac<16>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в правом фокусе.

2.322. Для правой ветви гиперболы $\frac<16>-\frac<9>=1$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится

а) в левом фокусе, б) в правом фокусе.

2.323. Для параболы $y^2=6x$ написать полярное уравнение, считая, что полярная ось сонаправлена с осью абсцисс, а полюс находится в фокусе параболы.

2.324 (б, в) Написать канонические уравнения следующих кривых второго порядка:

Ответ: а) $\frac<16>-\frac<9>=1,$ б) $y^2=6x.$

2.327. Вывести полярное уравнение параболы $y^2=2px$ при условии, что полярная ось сонаправленна с осью $Ox,$ а полюс находится в вершине параболы.