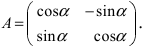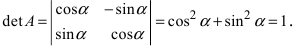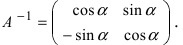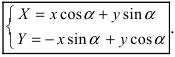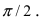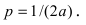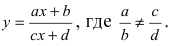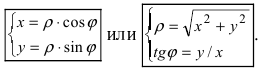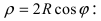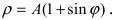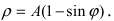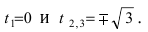Перевести уравнение в прямоугольную систему координат

Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно

Страница содержит онлайн калькуляторы для перехода от географических координат к плоским прямоугольным координатам Гаусса и обратно (используются формулы для референц-эллипсоида Красовского).

Плоские прямоугольные координаты Гаусса х и у связаны с географическими координатами φ (широта) и λ (долгота) точек земной поверхности довольно сложными формулами (ключами перехода). Ниже представлены два калькулятора, которые осуществляют переход от одних координат к другим.

Данные калькуляторы используют ключи перехода, рассчитанные для референц-эллипсоида Красовского, или системы координат СК-42. Использование СК-42 допускается только до 1 января 2021 года, так что эти калькуляторы представляют, скорее, исторический интерес.

Переход от географических координат к плоским прямоугольным координатам Гаусса-Крюгера

Переход от плоских прямоугольных координат Гаусса-Крюгера к географическим координатам

Зональная система плоских прямоугольных координат Гаусса

В топографии и геодезии широко распространено использование прямоугольных координат. Просто потому, что километрами и метрами пользоваться проще чем градусами, минутами и секундами. В качестве системы плоских прямоугольных координат обычно используют систему плоских прямоугольных координат Гаусса, основанную на проекции Гаусса-Крюгера (в 1825-1830 годах Гаусс разработал поперечно-цилиндрическую конформную (равноугольную) проекцию эллипсоида на плоскость, а Крюгер в 1912 году вывел для нее рабочие формулы вычислений).

Суть, если вкратце в том, что земной эллипсоид разбивают меридианами на сферические двуугольники – зоны. Затем каждую зону проектируют на внутреннюю боковую поверхность цилиндра, развернув который,
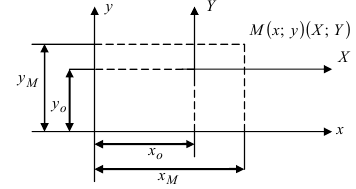
получают проекцию поверхности Земли. Ширина зоны — 6 градусов, то есть всего существует 60 зон. В России зоны отсчитываются от нулевого меридиана (осевой меридиан первой зоны — 3 градуса восточной долготы). Внутри каждой зоны действует своя система координат, включающая номер зоны. Ширина любой координатной зоны составляет на экваторе примерно 670 км, на широте 40° — 510 км, на широте 50° — 430 км. Координата x, направленная вдоль меридиана в северном полушарии всегда положительна, чтобы сделать и координату y положительной, начало координат смещают на 500 км левее осевого меридиана. См. иллюстрацию ниже (оригинальный источник изображения неизвестен).

Преобразования декартовой системы координат с примерами решения

Содержание:

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 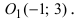Вычислить положение точки М в новой системе отсчета.

Решение:

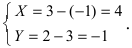
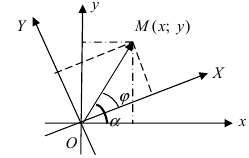
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 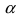(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

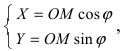
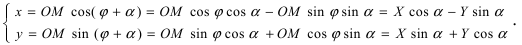
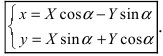
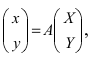
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 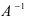обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

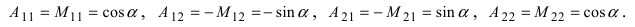
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 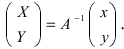Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 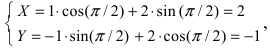т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

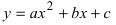
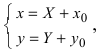
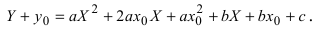
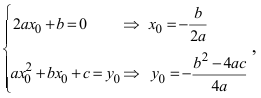
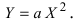
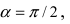
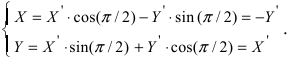
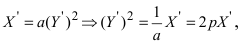
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 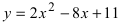к каноническому виду.

Решение:

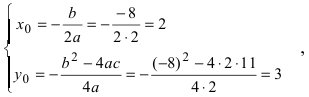
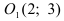
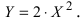
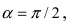
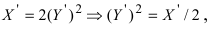
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

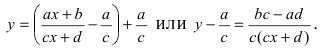
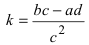
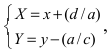
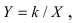
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

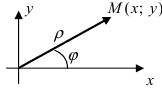
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 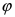между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

Главными значениями угла 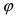являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

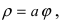
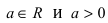
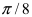
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

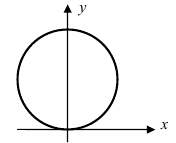
2. Уравнение окружности: уравнение 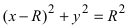описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

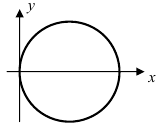
3. Уравнение 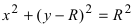описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

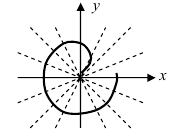
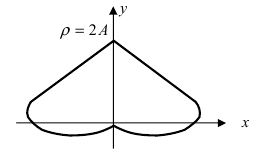
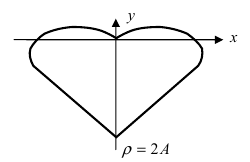
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

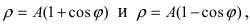
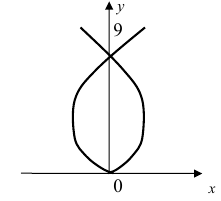
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

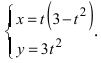
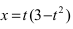
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

• Бесконечно малые и бесконечно большие функции
• Замечательные пределы
• Непрерывность функций и точки разрыва
• Точки разрыва и их классификация
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Цилиндрическая система координат (цилиндрические координаты)

Для введения цилиндрической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла, наблюдаемое со стороны положительного направления оси , происходило против часовой стрелки (рис.2.34,а).

В цилиндрической системе координат положение точки , не принадлежащей оси аппликат, характеризуется полярными координатами точки — ортогональной проекции точки на основную плоскость, и аппликатой — координатой точки — ортогональной проекции точки на ось аппликат. Таким образом, цилиндрические координаты точки — это упорядоченная тройка чисел — полярный радиус , полярный угол и аппликата . У точек, принадлежащих оси аппликат, не определен полярный угол, они задаются указанием нулевого полярного радиуса и аппликатой.

Переход от цилиндрических координат к декартовым (прямоугольным)

С цилиндрической системой координат можно связать прямоугольную систему координат (рис.2.34,б), у которой начало и базисные векторы совпадают с началом цилиндрической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим цилиндрическую систему координат ( связанную с данной прямоугольной ).

Поскольку аппликата точки в прямоугольной системе координат и аппликата в цилиндрической системе координат совпадают, то формулы, связывающие между собой прямоугольные координаты точки и ее цилиндрические координаты , имеют вид, следующий из

Эти формулы перехода позволяют найти прямоугольные координаты по известным цилиндрическим. Обратный переход выполняется по формулам

Главное значение полярного угла находится по формулам (см. рис.2.29).

Пример 2.12. В цилиндрической системе координат :

а) построить координатные поверхности ;

б) найти цилиндрические координаты точки , если известны ее прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны ее цилиндрические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного радиуса , является прямой круговой цилиндр, ось которого параллельна оси аппликат (рис.2.35). Этим объясняется название цилиндрической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении полярного угла , является полуплоскость, ограниченная осью аппликат (на рис.2.35 изображены полуплоскости и ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении аппликаты , является плоскость, перпендикулярная оси аппликат (на рис.2.35 изображены плоскости и ).

б) Найдем цилиндрические координаты точки . Аппликата , полярный радиус и полярный угол находим по формулам (2.20) (см. пример 2.11):

так как и ортогональная проекция точки на координатную плоскость (основную плоскость) лежит в IV четверти.

в) Найдем прямоугольные координаты точки . По формулам (2.19) вычисляем (см. пример 2.10):