Перевод параметрического уравнения плоскости в каноническое

Перевод параметрического уравнения плоскости в каноническое

Пусть в декартовой системе координат дан вектор n = и точка М 0 =( x 0 , y 0 , z 0 ).

Построим плоскость Π, проходящую через т. М 0 , перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М Π ó М 0 М n .

М 0 М= < x-x 0 , y-y 0 , z-z 0 > n ó A( x-x 0 )+B( y-y 0 )+C( z-z 0 )=0. (*)

Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x 0 -B y 0 -C z 0 .

Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n= <3,1,1>и проходящей через точку М(2,-1,1).

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

Пусть в декартовой системе координат дан вектор a =и точка М 0 =( x 0 , y 0 , z 0 ).

Построим прямую l , проходящую через т. М 0 , параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М l ó М 0 М || a .

М 0 М= < x-x 0 , y-y 0 , z-z 0 >|| a ó t R , т.ч. М 0 М=t ·a =>

Параметрические уравнения прямой в пространстве:

(**)

Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t 0 =0 он находится в точке М 0 , в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М 1 =(x 1 ,y 1 ,z 1 ).

Утверждение 3: расстояние от точки М 1 до плоскости Π вычисляется по формуле:

Пример 6. Найти расстояние от точки до плоскости.

Пусть в декартовой системе координат М 1 =(x 1 ,y 1 ,z 1 ), М 2 =(x 2 ,y 2 ,z 2 ) .

Утверждение 4: Координаты т. М, т.ч. М 1 М=λ∙ММ 2 , находятся по следующим формулам:

.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Параметрическое уравнение прямой на плоскости

В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.

Параметрическое уравнение прямой L на плоскости представляется следующей формулой:

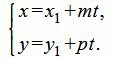(1)

Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.

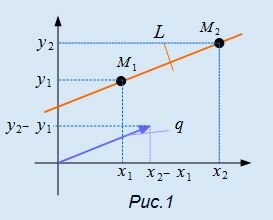
Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M₁(x₁, y₁) при t=1, получим точку M₂(x₁+m, y₁+p).

Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M₁ и M₂: m=x₂−x₁, p=y₂−y₁(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).

Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x₂−x₁, p=y₂−y₁ в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M₁(x₁, y₁) и M₂(x₂, y₂):

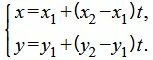(2)

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить параметрическое уравнение прямой.

Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

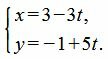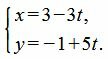Пример 2. Прямая проходит через точки M₁=(−5, 2) и M₂=(−2, 3). Построить параметрическое уравнение прямой.

Решение. Воспользуемся формулой (2). Подставим координаты точек M₁ и M₂ в уравнение (2):

Упростим полученное уравнение:

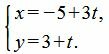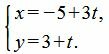Приведение параметрического уравнения на плоскости к каноническому виду

Выразим параметр t в (1) через переменные x и y:

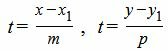(3)

Из выражений (3), можем записать каноническое уравнение прямой на плоскости:

.

(4)

Обратное преобразование смотрите здесь.

Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:

Привести данное уравнение прямой к каноническому виду.

Решение: Выразим параметр t через переменные x и y:

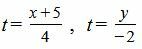(5)

Из выражений (5), можем записать:

Приведение параметрического уравнения на плоскости к общему виду

Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:

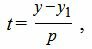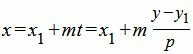(6)

Умножим обе части уравнения (6) на p и группируем элементы уравнения:

.

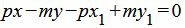(7)

Сделаем обозначения: A=p, B=−m, C=−px₁+my₁. Тогда получим общее уравнение прямой:

Обратное преобразование смотрите здесь.

Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:

(9)

Привести данное уравнение прямой к общему виду.

Решение: В уравнении (9) имеем: x₁=−5, y₁=0, m=4, p=−2. Подставим эти значения в формулу (7):

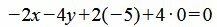(10)

Упростив выражение (10) получим общее уравнение прямой (9):

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными , если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам .

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим — радиус-векторы точек и (рис.4.16).

Условие компланарности векторов (рис.4.16) можно записать, используя свойства смешанного произведения Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

Параметрическое уравнение плоскости

Пусть в координатном пространстве заданы:

б) два неколлинеарных вектора (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам и проходящей через точку

Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы и компланарны (см. разд. 1.3.2). Запишем условие компланарности: где — некоторые действительные числа (параметры). Учитывая, что получим векторное параметрическое уравнение плоскости :

где — направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

где и — координаты направляющих векторов и соответственно. Параметры в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины пропорциональны расстоянию от заданной точки до точки принадлежащей плоскости. При точка совпадает с заданной точкой . При возрастании (или ) точка перемещается в направлении вектора (или ), а при убывании (или ) — в противоположном направлении.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор , коллинеарный плоскости, ортогонален нормальному вектору для этой плоскости. Поэтому их скалярное произведение равно нулю:

Следовательно, координаты и направляющих векторов и плоскости и ее нормали связаны однородными уравнениями:

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение уравнения определяя тем самым координаты точки принадлежащей плоскости;

2) найти любые два линейно независимых решения однородного уравнения определяя тем самым координаты решения и направляющих векторов и плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему , достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

и записать общее уравнение плоскости в форме (4.14):

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве (в прямоугольной системе координат) заданы точки и (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам и

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Составим параметрическое уравнение:

1) находим любое решение уравнения , например, следовательно, точка принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения например и следовательно, векторы являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

б) Координаты середины отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов и

Составляем уравнение (4.14):

Тот же результат можно получить, записывая уравнение (4.18):