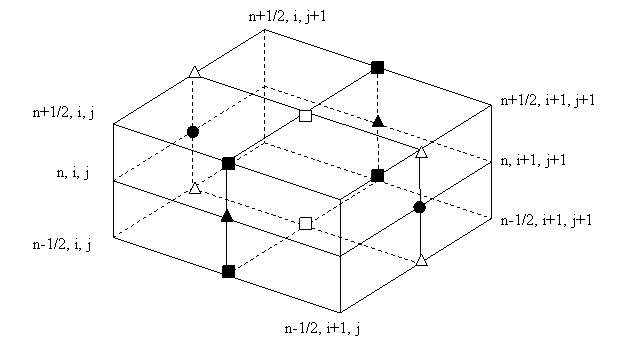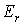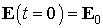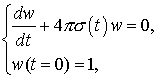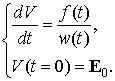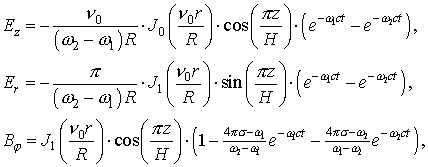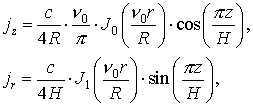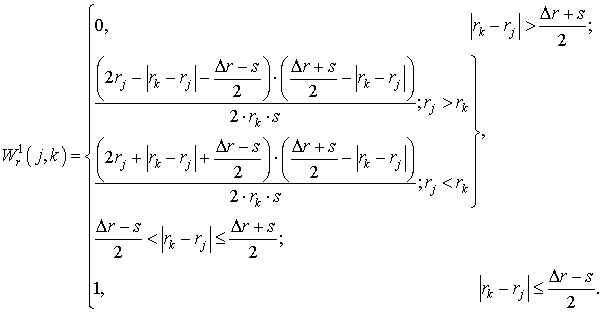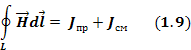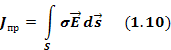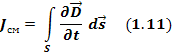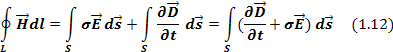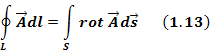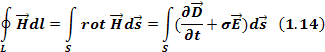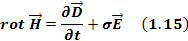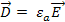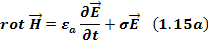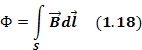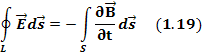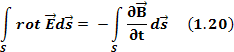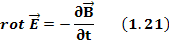Численное моделирование возбуждения электромагнитных полей в цилиндрической полости потоком релятивистских электронов
( Numerical Simulation of Electromagnetic Fields Generation in the Cylindrical Cavity by Relativistic Electron Flux
Preprint, Inst. Appl. Math., the Russian Academy of Science)
Егорушкин А.А., Крюков А.А., Скачков М.В.
(A.A.Yegorushkin, A.A.Krukov, M.V.Skachkov)
ИПМ им. М.В.Келдыша РАН
Москва, 2005
Аннотация
Рассмотрен эксперимент, в котором аксиально-симметричный поток релятивистских электронов инжектируется с торца в цилиндрическую камеру (материал – Fe), заполненную воздухом. Математическая модель эксперимента включает двумерные нестационарные уравнения Максвелла в цилиндрических координатах; уравнения для вычисления проводимости воздушной среды в камере; моделирование потока релятивистских электронов методом крупных частиц. При численном интегрировании уравнений Максвелла используется идеология метода квазианалитической интерполяции. В методе крупных частиц расчёт плотности тока основывается на законе сохранения заряда в ячейках. Предложен и реализован подход к распараллеливанию вычислительного алгоритма на многопроцессорной вычислительной технике с распределённой памятью, который принципиально отличается от геометрического распараллеливания и использует тот факт, что моделирование крупных частиц занимает основное расчётное время.
Abstract
The experiment, which is in the axial-symmetric relativistic electron flux injecting from the end face into the cylindrical chamber (material – Fe) filled with the air, is considered. The mathematical model contains the 2-D non-stationary Maxwell equations in cylindrical coordinate system, the equations for computing the air conductivity in the chamber and the particle simulation algorithm for the relativistic electron flux. For integrating the Maxwell equations the quasianalitic interpolation technique is used. The computation of the current density that is realized in the particle simulation algorithm is based on the charge conservation in grid cells. The technique of the parallel computations at multiprocessor with distributed memory is proposed. This technique is different from the geometric method and uses the fact that the particle simulation algorithm occupies the basic time of computations.
Возбуждение электромагнитных полей в полостях технологических объектов, находящихся под воздействием гамма-излучения, определяется комптоновской ионизацией материалов. В результате ионизации возникает поток комптоновских электронов высоких энергий, который, в свою очередь, взаимодействует с молекулами нейтрального газа, заполняющего полости, и образует потоки вторичных электронов. Возникающие при этом электромагнитные колебания влияют на функционирование электронной аппаратуры объектов.
Разработка адекватной математической модели указанных физических процессов и построение вычислительных алгоритмов в сложной геометрии является нетривиальной задачей. В связи с этим актуальными становятся разработка и исследование математических моделей конкретных физических экспериментов, построение численных методик расчёта электромагнитных полей и проведение на их основе численного эксперимента. Численный эксперимент позволит более детально изучать отдельные этапы эволюции физических процессов и путём сравнения с результатами физических экспериментов выбрать адекватную математическую модель.
В настоящей работе рассматривается эксперимент, в котором аксиально-симметричный поток гамма-квантов проникает сквозь торец в цилиндрическую камеру (материал – Fe ), заполненную воздушной средой. Ось потока совпадает с осью камеры. Процесс взаимодействия гамма-квантов с торцом камеры и образование потока комптоновских релятивистских электронов моделируется методом Монте – Карло [1], его описание выходит за рамки настоящей работы. В работе этот поток считается заданным, т. е. в камеру инжектируется аксиально-симметричный пучок релятивистских электронов.
Математическая модель рассматриваемого эксперимента включает три взаимосвязанные подзадачи.
1. Задача для двумерных нестационарных уравнений Максвелла в цилиндрических координатах с граничными и начальными условиями.
2. Вычисление проводимости воздушной среды в камере.
3. Моделирование потока релятивистских электронов методом крупных частиц.
При численной реализации модели были решены следующие проблемы.
Во-первых, в зависимости от интенсивности потока релятивистских электронов возможны процесс лавинной ионизации воздушной среды в камере и, как следствие, большая проводимость. Поэтому численные методики интегрирования уравнений Максвелла и уравнений для вычисления проводимости должны быть адаптированы к этим процессам. В настоящей работе для этой цели используется идеология метода квазианалитической интерполяции [2].
Во-вторых, стандартные процедуры вычисления плотности тока в методе крупных частиц не обеспечивают сохранение заряда в ячейках, что в случае малой проводимости воздушной среды может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля [3]. Поэтому в работе предлагается методика расчёта плотности тока, основанная на законе сохранения заряда в ячейках.
В-третьих, в силу цилиндрической симметрии расчётной сетки возникает проблема со взвешиванием заряда частиц вблизи оси симметрии. Стандартные процедуры взвешивания не дают удовлетворительного результата в осевых ячейках. Простая интерполяция из соседних не осевых ячеек не годится, так как требуется выполнение закона сохранения заряда в ячейках. В работе предлагается процедура взвешивания, дающая правильный результат в осевых ячейках.
В-четвёртых, предложен и реализован подход к распараллеливанию вычислительного алгоритма, который принципиально отличается от геометрического распараллеливания и использует тот факт, что моделирование крупных частиц занимает основное расчётное время.
§1. Математическая модель
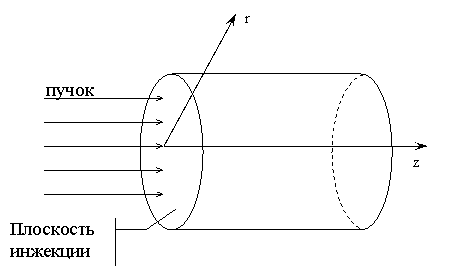
Рассматривается эксперимент, в котором аксиально-симметричный пучок релятивистских электронов инжектируется в цилиндрическую камеру, заполненную нейтральной воздушной средой (рис.1). Ось пучка совпадает с осью камеры. Давление в камере Р=1атм. Математическая модель эксперимента включает следующие взаимосвязанные подзадачи.
SHAPE \* MERGEFORMAT
1. Уравнения Максвелла в цилиндрических координатах с граничными и начальными условиями:
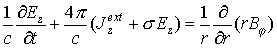
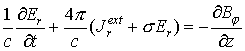
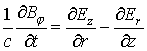
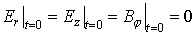
2. Уравнения движения релятивистских электронов
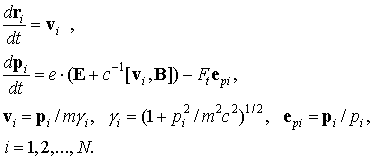
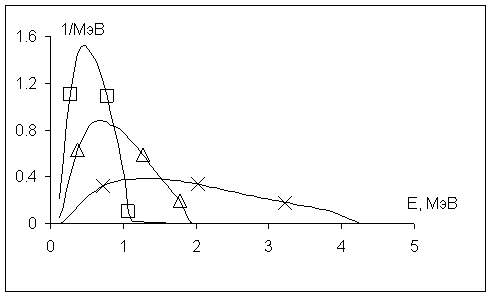
Начальные координаты электронов распределены в плоскости инжекции ( z = 0) равномерно по сечению. Начальные скорости отвечают энергетическому спектру электронов в пучке. Сила ионизационного торможения Ft описывается формулой Бета – Блоха:
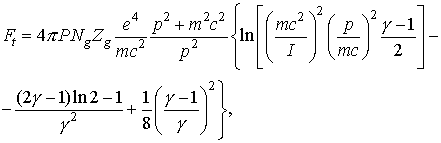
где Р – давление в атм., 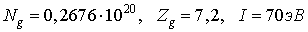

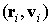
3. Уравнения для вычисления проводимости воздушной среды в камере:
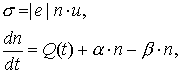
где n – концентрация электронов проводимости, Q ( t ) – источник вторичной ионизации (вычисляется с использованием метода крупных частиц), u ( P , E ) – подвижность электронов проводимости, a ( P , E ) – скорость вторичной ионизации (значения величин u ( P , E ) и a ( P , E ) посчитаны по методике, изложенной в работе [4], и содержатся в таблицах),
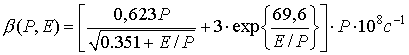
§2. Численное интегрирование уравнений Максвелла и уравнения для вычисления проводимости воздушной среды
Для разностной аппроксимации системы уравнений (1) используется вариант явной схемы «крест». Вводится равномерная сетка по времени 
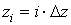
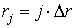
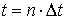
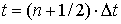
SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT

SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT
Пространственные производные заменяются центрально-симметричными разностными соотношениями
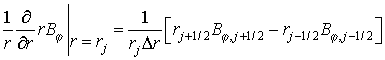

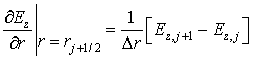
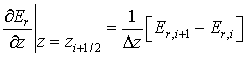
При интегрировании по времени используется идеология метода квазианалитической интерполяции [2]. Для аппроксимации дифференциального уравнения с начальным условием
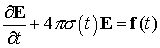
вводится вспомогательная функция 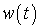
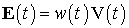
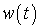
решив которую получим
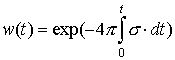
Тогда 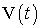
Интегрируя это уравнение и аппроксимируя интеграл по времени, получим разностную запись исходного уравнения
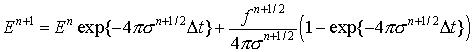
Такой метод обеспечивает первый порядок аппроксимации по D t в пределе 
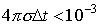
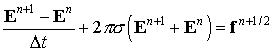
Была рассчитана следующая тестовая задача:
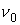
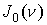
Метод квазианалитической интерполяции используется также при интегрировании уравнения (4):
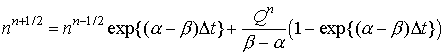
Необходимость в использовании квазианалитической интерполяции диктуется тем обстоятельством, что при E > 100 СГСЕ значение a велико.
§3. Моделирование потока релятивистских электронов методом крупных частиц
Численное интегрирование уравнений движения (2) проводится по методу, аналогичному методу Бориса [5]:
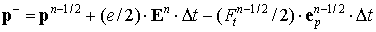

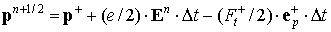
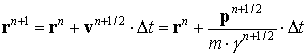
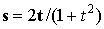
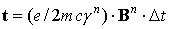
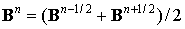
Здесь компоненты поля билинейно интерполированы с узлов пространственной сетки на координаты частиц. В алгоритме на каждом шаге по времени проводится проверка неравенства
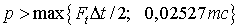
В случае нарушения этого неравенства электрон считается поглотившимся и его дальнейшее движение не рассматривается. Метод Бориса был выбран в связи с тем, что он полностью учитывает тот факт, что магнитное поле изменяет направление движения электрона, но не изменяет его энергию.
Метод крупных частиц, использованный для вычисления плотности тока 
3.1. Расчёт плотности тока в узлах расчётной сетки базируется на законе сохранения заряда в ячейках и основывается на методике работы [3]. Соблюдение закона сохранения заряда в ячейках особенно важно обеспечить в случае малой проводимости воздушной среды. В этом случае метод крупных частиц, не обеспечивающий сохранение заряда в ячейках, может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля.
Стандартные процедуры вычисления плотности тока в узлах 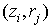
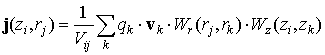
где 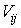
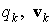
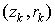
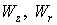
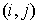
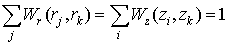
Эти процедуры не обеспечивают сохранение заряда в ячейках.
В работе предлагается другой алгоритм вычисления плотности тока, аналогичный алгоритму из [3]. В этом алгоритме производится подсчёт заряда, перенесённого каждой частицей через границу пространственной ячейки за один шаг по времени. Полученные значения суммируются по частицам, делятся на площадь границы и приравниваются к плотности тока в узле расчётной сетки на границе ячейки.
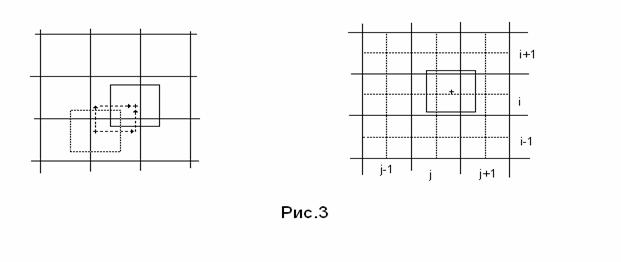
Подсчёт заряда, перенесённого одной частицей через границу ячейки за один шаг по времени, проводится следующим образом. Предположим, что частица находится в ячейке 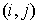
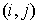
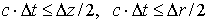
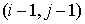
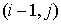
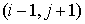

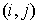
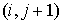
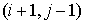
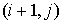
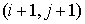
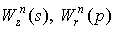
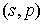

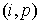
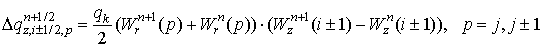
заряд, вынесенный из ячейки 
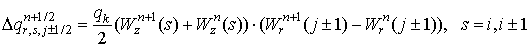
Предложенные формулы расчёта не являются единственно возможными. Они представляют собой полусумму результатов, полученных для двух вариантов движения частицы: смещение сначала параллельно оси z , а затем вдоль радиального направления до конечного положения частицы; смещение сначала вдоль радиального направления, а затем параллельно оси z (см. рис.3).
Для сглаживания электромагнитных шумов предложенный алгоритм вычисления плотности тока необходимо дополнить процедурой усреднения тока по характерному промежутку времени пролёта частицей пространственной ячейки [3]:
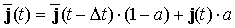
где 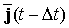
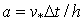
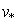
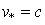
3.2. В силу цилиндрической симметрии возникает трудность, связанная с распределением заряда частиц вблизи оси. Кроме требования сохранения заряда частицы (7) форм-факторы должны обеспечивать правильный расчёт плотности тока в плоскости инжекции 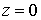
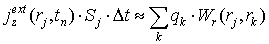
где 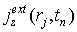
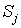
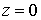

Начальные координаты электронов распределены в плоскости инжекции равномерно по r . Поэтому заряды инжектируемых частиц вычисляются по формуле:
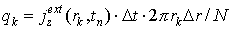
где N – число частиц, инжектируемых в одну ячейку за один шаг по времени. В пределе при 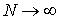
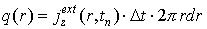
и в соотношении (8) суммирование заменяется интегрированием:
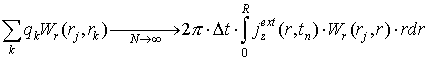
В предположении, что в пределах ячейки 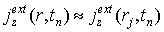
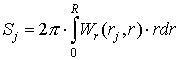
которому должна удовлетворять неотрицательная функция 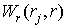
Рассмотрим два стандартных форм-фактора.
1. Взвешивание по модели CIC с равномерно заряженными крупными частицами.
2. Линейное взвешивание.
Здесь s – размер частицы. Функции 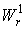
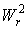
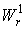
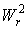
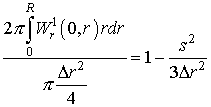
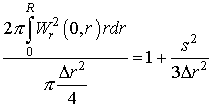
Из этих уравнений видно, что если в качестве искомой функции взять 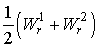
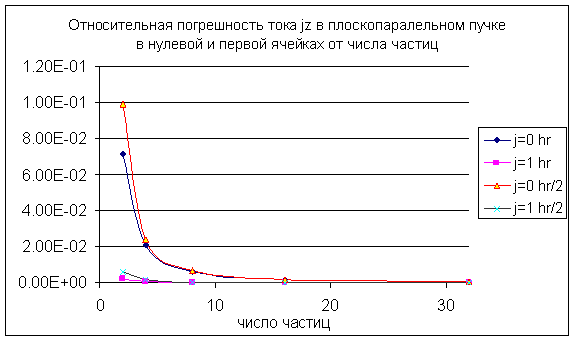
Ниже приведены расчетные данные для плоскопараллельного пучка (частицы движутся в направлении оси z ).
Использовались частицы размера hr и hr /2, 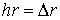
2.3. Для сглаживания флуктуаций плотности тока, вызванных дискретной структурой пучка, целесообразно распределять начальные координаты и скорости частиц с использованием последовательности точек, равномерно распределённых в трёхмерном единичном кубе. При этом обычные случайные числа не годятся из-за их большой дисперсии при малой выборке. Удовлетворительные результаты даёт использование обращённых двоичных, троичных и пятеричных дробей 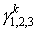
Последовательность точек 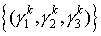
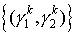
Опишем подробно процедуру инжекции крупных частиц в камеру в момент времени 
Пусть J – число ячеек в плоскости инжекции 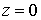
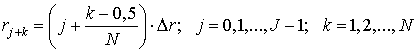
где N – число точек в пределах одной j -й ячейки. Число инжектируемых частиц увеличивается пропорционально номеру ячейки, т. е. с координатой 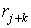
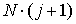
Начальные энергии и направления вылета электронов в j -й ячейке разыгрываются с использованием чисел 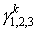
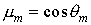
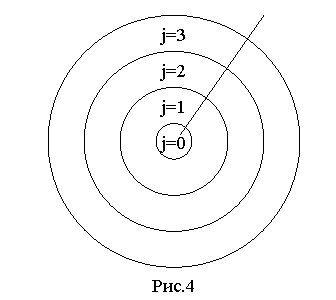
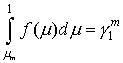
где 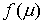
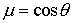
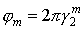
Начальная энергия электрона находится в результате решения уравнения:
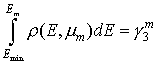
где 
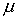

P – число шагов по времени между повторами в последовательности точек 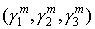
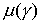
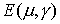
В связи с тем, что скорости электронов имели три компоненты, уравнения движения (2) интегрировались в декартовых координатах. Для расчёта плотности тока производился переход в цилиндрическую систему координат 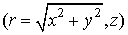

т. е. все частицы стартовали с одного луча. Такое описание применимо в аксиальной симметрии, когда точки на окружности 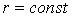
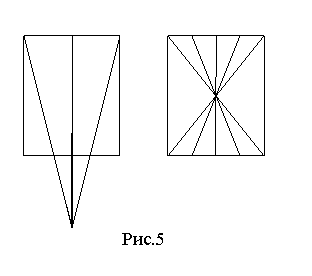
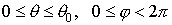
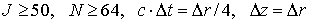
§4. Параллельная реализация вычислительного алгоритма на многопроцессорной вычислительной системе с распределённой памятью
Рассматриваемая в настоящей работе численная методика, реализующая метод крупных частиц, включает два основных блока:
1) решение уравнений Максвелла (1) сеточным методом и расчёт проводимости (4);
2) решение уравнений движения крупных частиц (2) (электронов пучка) и вычисление плотности тока пучка 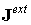
В процессе работы программы на каждом временном шаге блоки обмениваются данными. Этими данными являются массивы значений компонент электромагнитного поля, заполняемые в первом блоке и используемые во втором для решения уравнений движения электронов пучка, и плотность тока пучка 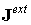
Просматриваются два основных подхода к распараллеливанию численной методики.
Первый подход – традиционное геометрическое распараллеливание. Расчётная область разбивается на подобласти, в каждой из которых за исключением границ задача решается самостоятельно. Эффективность распараллеливания существенно зависит от равномерности загрузки процессоров, обслуживающих разные подобласти. В связи с этим при реализации этого подхода возникает следующая трудность. Двум основным блокам численной методики требуются разные затраты временных ресурсов, которые отличаются на порядки. А именно, на моделирование движения частиц и их взвешивание на сетке требуется значительно больше времени, чем на разностное решение уравнений Максвелла. Это объясняется тем, что число крупных частиц много больше числа узлов пространственной расчётной сетки. В связи с этим равномерность загрузки процессоров жёстко связана с равномерностью распределения крупных частиц пучка в расчётной области. Однако в практических задачах ситуация усложняется тем, что пучок далеко не всегда занимает всю расчётную область. Он может находиться в некоторой её части и изменяться в пространстве и во времени (расширяться, сжиматься, деформироваться и т.п.).
Авторами настоящего препринта реализован второй подход к распараллеливанию численной методики, который использует тот факт, что моделирование крупных частиц занимает основное расчётное время. Число крупных частиц, приходящееся на одну пространственную ячейку, является дополнительной размерностью задачи. Поэтому если это число составляет сотни или тысячи единиц, то распараллеливание резонно проводить «по частицам», т.е. разделить всю совокупность крупных частиц на списки и распределить их по процессорам. Фактически это означает распараллеливание только второго блока численной методики, отвечающего за вычисление плотности тока пучка 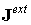
Организация обменных операций при распараллеливании «по частицам» принципиально отличается от геометрического распараллеливания. В геометрическом распараллеливании обмены осуществляются между двумя процессорами, обслуживающими соседние пространственные подобласти. В распараллеливании «по частицам» используются коллективные обмены.
Опишем схему организации обменов во втором подходе более детально. Пусть M – число процессоров, пронумерованных от 0 до ( M – 1). 0-ой процессор назовём головным ( root ). В головном процессоре реализуется первый блок численной методики, отвечающий за решение уравнений Максвелла. Выходными данными первого блока являются компоненты электромагнитного поля в узлах пространственной сетки, которые после вычисления на данном временном шаге распределяются по всем процессорам. Второй блок численной методики реализуется во всех процессорах, включая головной. Полный список крупных частиц пучка заранее разделён на M подобных списков, пучок расслаивается при этом на M одинаковых пучков. Процессор с номером i вычисляет плотность тока 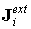
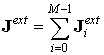
Затем происходит переход на следующий временной слой и алгоритм повторяется. Следует отметить, что такая схема организации обменов возможна благодаря тому, что частицы взаимодействуют друг с другом только на макро-уровне – через поле. Столкновения частиц не учитываются.
§5. Исходные данные и результаты расчётов
Результаты вычислительного эксперимента получены при следующих значениях исходных данных. Цилиндрическая камера (см. рис.1) имеет высоту H = 50 см и радиус R = 12,5 см . Плотность входного тока в плоскости инжекции z = 0 имеет вид:
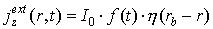
где 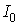
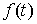
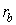
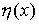
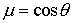

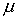

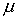
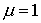
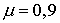
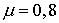
Основной расчёт проводился на 64 процессорах многопроцессорной вычислительной системы МВС-1000М и занял 220 мин. При этом на хранение текущей информации о координатах, импульсах и зарядах крупных частиц потребовалось по 150 Мбайт оперативной памяти на каждом процессоре. Таким образом, если бы тот же расчёт целиком проводить на одном процессоре, то потребовалось бы около 10 Гбайт оперативной памяти. Такой объём оперативной памяти не мог быть выделен одному процессору. Для оценки эффективности распараллеливания вычислительного алгоритма был проведён расчёт задачи на 32 процессорах. Общее время вычислений оказалось равным 410 мин, что указывает на то, что эффективность распараллеливания вычислений не менее 90%.
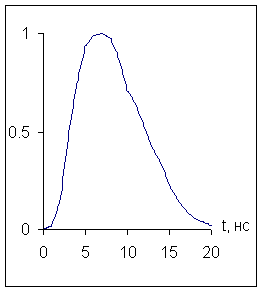
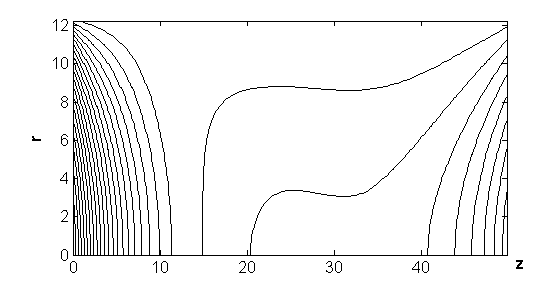
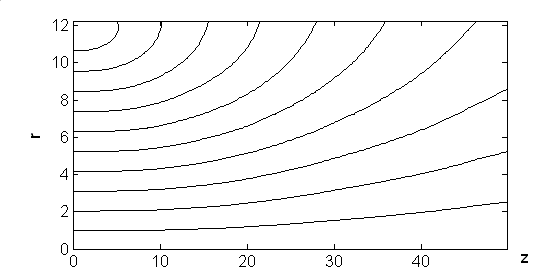
На рис.9 показаны линии уровня максимального по времени модуля z -компоненты напряжённости электрического поля 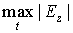
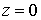

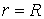
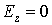
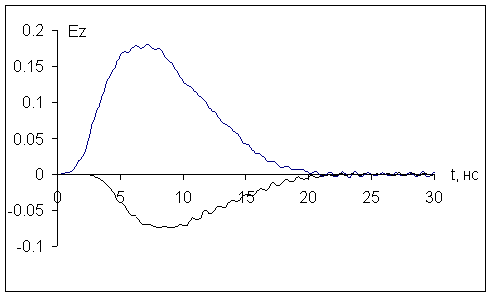
На рис.10 изображены зависимости от времени z -компоненты напряжённости электрического поля 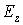
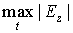
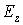
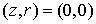
На рис.11 показаны линии уровня максимального по времени модуля напряжённости магнитного поля 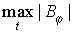
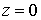
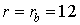
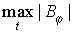
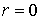
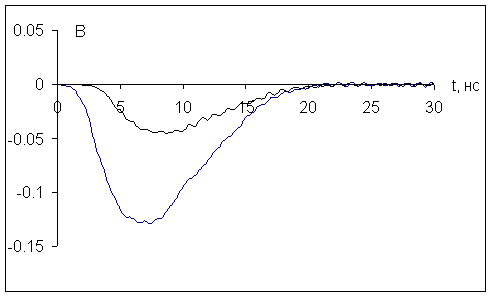
На рис.12 приведены зависимости от времени напряжённости магнитного поля в двух точках 
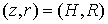
Приведённые результаты вычислительного эксперимента сравнивались с предварительными результатами физического эксперимента. Сравнение показало на удовлетворительное совпадение амплитуд электрического поля, полученных в физическом эксперименте, с результатами численных расчётов.
Авторы выражают признательность к. ф.-м. н. М. Е. Жуковскому за предоставленные исходные данные для вычислительного эксперимента, постоянное внимание и помощь в работе.
1. М.Е.Жуковский, С.В.Подоляко, Р.В.Усков. Алгоритм расчёта простран-ственного и спектрального распределений электронов, порождённых при взаимодействии проникающего излучения с объектами. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2004, препр. №89, 16с.
2. В.Я.Арсенин, Г.Д.Васильков. О разностных схемах для дифференциаль-ных уравнений с диссипативными членами. – М.: Ин. прикл. матем. им. М.В.Келдыша АН СССР, 1981, препр. №17, 20с.
3. М.В.Скачков. О проблеме шумов и сохранения заряда в методе крупных частиц. // Матем. моделирование, 2000, т.12, №9, с.96-108.
4. А.В.Березин и др. О математических моделях вторичной ионизации. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2002, препр. №29, 20с.
5. J.P.Boris. Relativistic Plasma Simulation-Optimization of a Hybrid Code // Proc. Fourth. Conf. Num. Sim. Plasmas, Naval Res. Lab., Wash D.C., 2-3 November 1970, p.3-67.
6. Ч.Бэдсэл, А.Ленгдон. Физика плазмы и численное моделирование. М.: Электроатомиздат, 1989, 455с.
Первое уравнение максвелла в цилиндрической системе координат
Теория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента.
Теория Максвелла — макроскопическая. Это означает, что рассматриваются макроскопические поля зарядов и токов, пространственные размеры которых неизмеримо больше размеров отдельных молекул и атомов.
Математическим выражением теории Максвелла служит система из четырех уравнений, которые записывают в двух формах — дифференциальной и интегральной.
Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.
Рассмотрим теорему Остроградского-Гаусса .
Пусть для характеристики какого-либо поля выбран вектор . Тогда поток вектора через произвольную замкнутую поверхность S, мысленно проведенную в этом поле, равен интегралу от дивергенции вектора , взятому по объему V, ограниченному замкнутой поверхностью S:
| (4.1.1) |
Операция дивергенции над произвольным вектором сводится к пространственной производной вида:
| (4.1.2) |
где ax, ay, az — проекции вектора на оси прямоугольной декартовой системы координат.
Рассмотрим теорему Стокса .
Пусть для характеристики какого-либо поля выбран вектор . Тогда циркуляция вектора вдоль произвольного замкнутого контура L, мысленно проведенного в этом поле, равна потоку вектора rot через поверхность S, ограниченную замкнутым контуром L:
| (4.1.3) |
Векторная операция rot в декартовых координатах выражается так:
| (4.1.4) |
Первое уравнение Максвелла
Это уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:
| (4.1.5) |
Однако для произвольного контура выполняется взаимосвязь:
| (4.1.6) |
Поскольку в общем случае , то для не изменяющегося во времени контура имеет место соотношение:
| (4.1.7) |
Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:
| (4.1.8) |
Используя теорему Стокса, преобразуем (4.1.5):
| (4.1.9) |
Сравнивая подинтегральные выражения в (4.1.7) и в правой части (4.1.9), получим окончательно первое уравнение Максвелла в дифференциальной форме:
| (4.1.10) |
Физический смысл этого уравнения: переменное магнитное поле индуцирует вихревое электрическое поле.
Второе уравнение Максвелла
Используем теорему Гаусса для диэлектриков:
| (4.1.11) |
где — вектор электрической индукции, — вектор поляризации диэлектрика.
Продифференцируем (4.1.11) по времени:
| (4.1.12) |
Если поверхность S — неподвижна и не деформируется, то изменение во времени потока вектора электрической индукции может быть связано только с изменением по времени самого вектора электрической индукции:
| (4.1.13) |
Правая часть этой формулы имеет размерность тока, следовательно, величина имеет размерность плотности тока. Максвелл предложил назвать эту величину плотностью тока смещения :
| (4.1.14) |
Введя представление о токе смещения, Максвелл по-новому подошел к рассмотрению условия замкнутости цепей электрического тока. Как известно, цепи постоянного тока должны быть замкнутыми. Однако для цепей переменного тока это условие уже не является обязательным. Например, при зарядке и разрядке конденсатора постоянный электрический ток протекает по проводнику, соединяющему обкладки, но не проходит через диэлектрик, находящийся между обкладками. Следовательно, цепь не замкнута. Однако, с точки зрения Максвелла, для переменного тока такая цепь замыкается благодаря току смещения, который протекает через такой участок, где нет проводника, т.е. через диэлектрик. На таком участке благодаря наличию переменного тока смещения обязательно возникает переменное магнитное поле. Однако действие тока смещения, приводящее к возникновению магнитного поля, нельзя отделить от действия обычного тока проводимости. Например, для прямолинейного тока проводимости можно записать:
| (4.1.15) |
Линии магнитного поля направлены по касательным к концентрическим окружностям, окружающим проводник с током. Найдем циркуляцию магнитного поля по замкнутому контуру в виде окружности радиуса r:
| (4.1.16) |
Следовательно, магнитное поле прямолинейного проводника — вихревое (циркуляция вектора магнитного поля по замкнутому контуру не равна нулю).
Максвелл предположил, что в правой части соотношения (4.1.16) следует добавить ток смещения:
| (4.1.17) |
где ток смещения легко вычислить, используя (4.1.14):
| (4.1.18) |
Силу тока проводимости можно также представить в виде:
| (4.1.19) |
Согласно теореме Стокса для магнитного поля, имеем:
| (4.1.20) |
Подставляя (4.1.18) и (4.1.19) в (4.1.17) и сравнивая подинтегральные выражения в правой и левой частях, получаем второе уравнение Максвелла:
| (4.1.21) |
При отсутствии тока проводимости, тем не менее, может существовать переменное магнитное поле, обусловленное только током смещения:
| (4.1.22) |
Третье уравнение Максвелла
Максвелл обобщил теорему Гаусса для диэлектриков (4.1.11), предположив, что она справедлива для любого электрического поля, как стационарного, так и переменного. Запишем уравнение (4.1.11) в виде:
| (4.1.23) |
где ρсвоб — объемная плотность свободных зарядов, расположенных в объеме V, ограниченном замкнутой поверхностью S.
Тогда, используя теорему Остроградского-Гаусса для вектора электрической индукции, получим:
| (4.1.24) |
Сравнивая подинтегральные выражения в (4.1.23) и (4.1.24), получим третье уравнение Максвелла:
| (4.1.25) |
Четвертое уравнение Максвелла
Поскольку поток вектора магнитной индукции равен нулю:
| (4.1.26) |
то, используя теорему Остроградского-Гаусса для вектора магнитной индукции, легко получить четвертое уравнение Максвелла:
| (4.1.27) |
Такое равенство определяется отсутствием магнитных зарядов.
Итак, полная система уравнений Максвелла в дифференциальной форме включает в себя четыре дифференциальных уравнения:
| (4.1.28) |
Эту систему необходимо дополнить материальными уравнениями , которые характеризуют электрические, и магнитные свойства конкретных сред (веществ).
В случае изотропных несегнетоэлектрических и неферромагнитных сред и макроскопических токов, подчиняющихся закону Ома, эти уравнения в системе СИ имеют вид:
| (4.1.29) |
где ε0 и μ0 — электрическая и магнитная постоянные, ε и μ — относительная диэлектрическая и магнитная проницаемости среды, σ — удельная электропроводность вещества.
4.1.2. Свойства электромагнитных волн
Электромагнитной волной называется распространяющееся в пространстве с определенной скоростью электромагнитное поле. Как следует из уравнений Максвелла, переменное электрическое поле непременно порождает переменное магнитное поле, которое затем индуктирует переменное электрическое поле. Поэтому следует говорить о неразрывной связи переменных электрического и магнитного полей, называя это явление электромагнитным полем . Очевидно, что такой процесс должен происходить, циклически повторяясь, в течение неограниченного времени, если нет поглощения.
Существование электромагнитных волн непосредственно следует их уравнений Максвелла. Для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, эти уравнения приобретают вид:
| (4.1.30) |
Используя материальные уравнения (4.1.29), эти уравнения можно представить в виде:
| (4.1.31) |
Если записать эти уравнения в проекциях на оси декартовой системы координат, то получим:
| (4.1.33) |
| (4.1.34) |
Используя первое из уравнений (4.1.33), можно получить:
| (4.1.35) |
Следовательно, компонента Ех удовлетворяет волновому уравнению:
| (4.1.36) |
Если ввести обозначение для дифференциальной операции:
| (4.1.37) |
то волновое уравнение (4.1.37) можно представить в компактном виде:
| (4.1.38) |
Аналогичные уравнения могут быть получены и для всех других компонент электрического и магнитного полей. Суммируя результаты, окончательно можно представить волновые уравнения для электрического и магнитного полей в векторном виде:
| (4.1.39) |
Таким образом, переменное электромагнитное поле распространяется в среде в виде волн, фазовая скорость которых равна:
| (4.1.40) |
где
| (4.1.41) |
есть скорость электромагнитной волны в вакууме.
Оказалось, что с = 3·10 8 м/с, что совпадает со скоростью света в вакууме. Поэтому Максвелл задолго до экспериментального обнаружения электромагнитных волн (Г. Герц, 1888 г.) высказал гипотезу о том, что свет — это тоже электромагнитная волна.
Прямой проверкой можно показать, что решениями уравнений (4.1.39) служат плоские синусоидальные волны, которые удобно представить в форме Эйлера:
| (4.1.42) |
где ω — циклическая частота; — волновой вектор, перпендикулярный фронту плоской волны и задающий направление распространения волны; — радиус-вектор, задающий точки пространства.
Операция ротора может быть сведена к векторному произведению, например:
| (4.1.43) |
Тогда, используя решения (4.1.42), с помощью (4.1.43) имеем:
| (4.1.44) |
следовательно, применение этой операции сводится к векторному произведению.
Рассмотрим сейчас операцию:
| (4.1.45) |
Наконец, операцию дивергенции можно представить так:
| (4.1.46) |
Применяя результаты (4.1.44), (4.1.45) и (4.1.46) к уравнениям Максвелла (4.1.31), имеем:
или, окончательно:
| (4.1.47) |
Из двух последних уравнений (4.1.47) следует, что , что указывает на поперечность электромагнитной волны. Из первого уравнения (4.1.47) ясно, что вектор Н как результат векторного произведения, должен быть перпендикулярен плоскости, в которой лежат вектора и . Аналогично, из второго уравнения (4.1.47) следует, что вектор электрического поля должен быть перпендикулярен плоскости, в которой лежат вектора и . Окончательно получается, что для любой электромагнитной волны вектора , и составляют тройку ортогональных векторов (Рис. 4.1.1).
4.1.3. Шкала электромагнитных волн
В зависимости от частоты ν = ω/2π или длины волны в вакууме λ0 = с/ν, а также способа излучения и регистрации различают несколько видов электромагнитных волн:
- радиоволны;
- оптическое излучение;
- рентгеновское излучение;
- гамма-излучение.
Радиволнами называются электромагнитные волны, у которых длина волны в вакууме λ0 > 5·10 -5 м (ν 12 Гц). Весь диапазон радиоволн принято делить на 9 поддиапазонов (Табл. 4.1.1).
| Название диапазона радиоволн | Длина волны, м | Частота, Гц |
|---|---|---|
| Сверхдлинные | Более 10 4 | Менее 3·10 4 |
| Длинные | 10 4 ÷ 10 3 | 3·10 4 ÷ 3·10 5 |
| Средние | 10 3 ÷ 10 2 | 3·10 5 ÷ 3·10 6 |
| Короткие | 10 2 ÷ 10 | 3·10 6 ÷ 3·10 7 |
| Метровые | 10 ÷ 1 | 3·10 7 ÷ 3·10 8 |
| Дециметровые | 1 ÷ 0,1 | 3·10 8 ÷ 3·10 9 |
| Сантиметровые | 0,1 ÷ 0,01 | 3·10 9 ÷ 3·10 10 |
| Миллиметровые | 10 -2 ÷ 10 -3 | 3·10 10 ÷ 3·10 11 |
| Субмиллиметровые | 10 -3 ÷ 5·10 -5 | 3·10 11 ÷ 6·10 12 |
Оптическим излучением или светом называются электромагнитные волны, у которых длина волны в вакууме лежит в диапазоне 10 нм >λ0 > 1 мм (границы условны). К оптическому излучению относят инфракрасное, видимое и ультрафиолетовое излучения.
Инфракрасным (ИК) называются электромагнитные волны, испускаемые нагретыми телами, у которых длина волны в вакууме лежит в диапазоне 1 мм > λ0 > 770 нм.
Видимым излучением (светом) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 770 нм > λ0 > 380 нм. Свет способен вызывать зрительные ощущения в человеческом глазе.
Ультрафиолетовым излучением (УФ) называются электромагнитные волны, у которых длины волны в вакууме лежат в диапазоне 380 нм > λ0 > 10 нм.
Рентгеновским излучением (рентгеновскими лучами) называются электромагнитные волны, которые возникают при взаимодействии заряженных частиц и фотонов с атомами вещества. Оно характеризуется длинами волны в вакууме в диапазоне с условными границами (10-100 нм) > λ0 > (0,01-1 пм).
Гамма-излучением (γ-лучами) называются электромагнитные волны с длинами волны в вакууме 0,1 нм > λ0. Это излучение испускается возбужденными атомными ядрами при радиоактивных превращениях и ядерных реакциях, а также возникает при распаде частиц, аннигиляции пар «частица-античастица» и других процессах.
4.1.4. Световая волна
Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других — как поток особых частиц (фотонов).
В электромагнитной волне колеблются векторы электрического и магнитного полей. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются наличием колебаний электрического вектора, который называют в этом случае световым вектором . Его изменения в пространстве и времени задаются уравнением плоской волны:
| (4.1.48) |
Здесь r — расстояние, отсчитываемое вдоль направления распространения волны.
Отношение скорости световой волны в вакууме с к ее фазовой скорости v в некоторой прозрачной среде называется абсолютным показателем преломления этой среды:
| (4.1.49) |
Показатель преломления связан с относительными диэлектрической и магнитной проницаемостями соотношением:
| (4.1.50) |
Для подавляющего большинства прозрачных веществ величина μ ≈ 1. Поэтому можно считать, что выполняется:
| (4.1.51) |
Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим n будет более оптически плотной.
Длины волн видимого света в вакууме заключены в пределах:
| (4.1.52) |
В веществе длины волн будут другими. В случае колебаний с частотой ν длина волны света в вакууме равна:
| (4.1.53) |
Используя соотношение (4.1.49), имеем для длины света в веществе формулу:
| (4.1.54) |
Частоты видимого света лежат в пределах:
| (4.1.55) |
Модуль среднего по времени потока энергии, переносимого волной, называется интенсивностью света I в данной точке пространства. Интенсивность пропорциональна квадрату амплитуды волны:
| I ∼ A 2 | (4.1.56) |
Световая волна, как и другие электромагнитные волны, является поперечной, т.е. направления колебаний электрического и магнитного векторов перпендикулярны к направлению ее распространения. В естественном свете присутствуют все направления колебаний электрического и магнитного векторов. Если в волне присутствуют колебания электрического вектора только в одной плоскости (а магнитного вектора в перпендикулярной плоскости), такую волну называют плоскополяризованной (линейно поляризованной) . Есть и более сложные случаи поляризации волн — круговая и эллиптическая. В случае круговой поляризации электрический и магнитный векторы вращаются по кругу с частотой изменения волны.
4.1.5. Геометрическая оптика
Длины воспринимаемых глазом световых волн очень малы (∼10 -7 м), поэтому распространение видимого света в первом приближении можно рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых прямых линий, называемых лучами. В предельном случае, когда длина волны света λ→0, законы оптики можно сформулировать на языке геометрии.
Основу геометрической оптики составляют 4 закона:
- закон прямолинейного распространения света;
- закон независимости световых лучей;
- закон отражения света;
- закон преломления света.
Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно . Этот закон является приближенным: при прохождении света через очень малые отверстия, размеры которых сравнимы с диной волны света, наблюдается отклонение от прямолинейности, тем большее, чем меньше отверстие.
Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга . Это означает, что пересечение лучей не мешает каждому из них распространяться независимо друг от друга. Этот закон справедлив при не слишком больших интенсивностях световых волн.
В основу геометрической оптики был положен принцип Ферма : свет распространяется по такому пути, для прохождения которого ему требуется минимальное время .
Пусть для прохождения участка ds свету требуется время dt = ds/v, где v — скорость света в данной точке среды. Поскольку v = c/n, то получим:
| (4.1.57) |
Следовательно, время τ, необходимое для прохождения пути от точки 1 до точки 2 (Рис. 4.1.2), равно:
| (4.1.58) |
Рис. 4.1.2. К принципу Ферма
Имеющая размерность длины величина
| (4.1.59) |
называется оптической длиной пути . В однородной среде оптическая длина пути равна произведению геометрической длины пути на показатель преломления:
| (4.1.60) |
Следовательно,
| (4.1.61) |
Пропорциональность времени прохождения оптической длине пути дает возможность сформулировать принцип Ферма так: свет распространяется по такому пути, оптическая длина которого минимальна.
Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален при движении света из точки 1 в точку 2, окажется минимальным и в случае распространения света в обратном направлении.
Получим с помощью принципа Ферма законы отражения и преломления света. Пусть свет попадает из точки А в точку В, отразившись от поверхности MN (Рис. 4.1.3).
Рис. 4.1.3. Закон отражения света как следствие принципа Ферма
Прямой путь из А в В прегражден экраном Э. Среда, в которой распространяется луч, однородна, поэтому минимальность оптической длины пути сводится к минимальности геометрической длины пути. Геометрическая длина произвольно взятого пути равна АО’B = A’O’B, поскольку вспомогательная точка A’ является зеркальным отражением точки А, и АО’ = A’O’. Из Рис. 4.1.3 видно, что наименьшей длиной обладает путь луча, отразившегося в точке О, для которой угол отражения равен углу падения. При удалении точки O’ от точки О геометрическая длина пути неограниченно возрастает, что противоречит принципу Ферма. Этот результат можно записать так:
| (4.1.62) |
Соотношение (4.1.62) выражает закон отражения света : отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения равен углу падения.
Найдем точку, в которой должен преломиться луч, распространяясь от А к В, чтобы оптическая длина пути была минимальной (Рис. 4.1.4).
Рис. 4.1.4. К расчету закона преломления света из принципа Ферма
Для произвольного луча оптическая длина пути равна:
| (4.1.63) |
Чтобы найти минимальное значение оптической длины пути, продифференцируем L по х и приравняем производную к нулю:
| (4.1.64) |
Множители при n1 и n2 равны, соответственно, sinθ и sinθ». Поэтому получаем соотношение:
| (4.1.65) |
которое выражает закон преломления света. Используя взаимосвязь показателей преломления с фазовыми скоростями распространения света в средах, можно записать соотношение (4.1.65) в виде:
| (4.1.66) |
Следовательно, закон преломления света гласит: преломленный луч лежит в одной плоскости с падающим лучом и нормалью; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных веществ.
В (4.1.66) n12 — относительный показатель преломления второго вещества по отношению к первому. Из (4.1.65) видно, что при переходе света из оптически более плотной среды в оптически менее плотную луч удаляется от нормали к поверхности раздела сред. Увеличение угла падения сопровождается более быстрым ростом угла преломления, и при достижении некоторого предельного угла падения угол преломления будет равным 90°:
| (4.1.67) |
Отсюда:
| (4.1.68) |
При углах падения, лежащих в пределах от θпред пред до 90°, преломленной волны не существует, вся энергия падающей волны переходит в энергию отраженной волны. Это явление называется полным внутренним отражением.
| Вещество | Показатель преломления | Вещество | Показатель преломления |
|---|---|---|---|
| Воздух | 1,0003 | Стекло (крон) | 1,515 |
| Вода | 1,333 | Стекло (флинт) | 1,752 |
| Спирт (этиловый) | 1,362 | Алмаз | 2,420 |
Во многих оптических приборах для преломления света используются стеклянные призмы. На Рис. 4.1.5 показан ход луча монохроматического света в призме.
Рис. 4.1.5. Ход лучей в призме
После двукратного преломления луч оказывается отклоненным от первоначального положения на угол δ ( угол отклонения ). Угол θ, заключенный между преломляющими гранями, называется преломляющим углом . Угол δ зависит от преломляющего угла θ и показателя преломления призмы. Эта зависимость может быть легко показана для призмы с малым преломляющим углом θ (тонкой призмы) в случае малого угла падения α. Исходя из закона преломления и принимая значение показателя преломления воздуха равным единице, можно записать:
| (4.1.69) |
При малых углах α и θ углы α1, γ и γ1 также малы. Поэтому вместо (4.1.69) можно приближенно записать:
| (4.1.70) |
Из четырехугольника BQDE, в котором углы при В и D — прямые, найдем, что угол BED равен 180° — θ. Тогда из четырехугольника BСDE находим:
| (4.1.71) |
Отсюда
| (4.1.72) |
Угол δ из треугольника BED равен:
| (4.1.73) |
Подставляя в (4.1.72) результаты (4.1.73) и (4.1.70), получим окончательно:
| (4.1.74) |
4.1.6. Преломление в линзе
В практических применениях большое значение имеет преломление света на сферической границе раздела двух сред. Основная деталь оптических приборов — линза — обычно представляет собой стеклянное тело, ограниченное с двух сторон сферическими поверхностями. В частном случае одна из поверхностей линзы может быть плоской. Такую поверхность можно рассматривать как сферическую с бесконечно большим радиусом кривизны.
Линзы могут быть изготовлены не только из стекла, а из любого прозрачного вещества с показателем преломления, превышающим единицу, например, из кварца, каменной соли, пластмасс и других материалов. Поверхности линз могут быть и более сложной формы — цилиндрические, параболические и т.д.
Рассмотрим линзу, ограниченную двумя сферическими преломляющими поверхностями PO1Q и PO2Q (Рис. 4.1.6).
Рис. 4.1.6. Тонкая линза
Центр первой преломляющей поверхности PO1Q лежит в точке С1, центр второй поверхности PO2Q — в точке С2. Будем считать, что расстояние O1O2 мало по сравнению с O1С1 или O2С2. В таком случае точки O1 и O2 можно считать практически совпадающими с точкой О — оптического центра линзы. Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью , остальные — побочными осями .
Луч, идущий по какой-либо оптической оси, проходя через тонкую линзу, не меняет своего направления. Лучи, идущие параллельно главной оптической оси, после преломления в линзе пересекаются в одной точке F, расположенной на главной оптической оси и называемой главным фокусом .
Покажем, что лучи, исходящие под небольшими углами α из некоторой точки А, лежащей на главной оптической оси, собираются линзой в одну точку А1, расположенную также на этой оптической оси и называемую изображением точки А (Рис. 4.1.7).
Рис. 4.1.7. Преломление в тонкой линзе
Построим плоскости, касательные к поверхностям линзы в точках М и N (в местах падения луча на линзу и его выхода из линзы), и проведем в эти точки радиусы R1 и R2 кривизны поверхностей линзы. Тогда луч AMNA1 можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α1, β1 и толщины линзы, можно записать:
| | (4.1.75) |
где а и b — расстояния от источника света А и от его изображения А1 до оптического центра линзы.
Из треугольников АНА1 и ВЕВ1 следует, что:
| (4.1.76) |
Принимая во внимание формулы (4.1.75), получим:
| (4.1.77) |
Учтено, что для тонкой линзы h1 ≈ h2 ≈ h. Поскольку, согласно формуле (4.1.74) для тонкой призмы выполняется: θ = (n-1)δ, то, с помощью (4.1.77) имеем формулу линзы :
| (4.1.78) |
В эту формулу не входит величина h, что означает, что расстояние b не зависит от от положения точки М. Следовательно, все лучи, исходящие из точки А, соберутся после преломления разными частями линзы в одной точке А1 .
Если точка А находится бесконечно далеко от линзы (а = ∞), т.е. если лучи падают на линзу параллельно главной оптической оси, то, согласно формуле (4.1.78), имеем:
| (4.1.79) |
Величина b = f называется фокусным расстоянием линзы :
| (4.1.80) |
Фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.
Принимая во внимание (4.1.80), формулу линзы (4.1.78) можно сейчас переписать так:
| (4.1.81) |
Величина, обратная фокусному расстоянию, называется оптической силой линзы :
| (4.1.82) |
Оптическая сила выражается в диоптриях (дп). 1 дп — оптическая сила линзы с фокусным расстоянием в 1 м.
4.1.7. Принцип Гюйгенса
В приближении геометрической оптики свет за преградой не должен проникать в область геометрической тени. В действительности световая волна распространяется во всем пространстве за преградой, проникая проникать в область геометрической тени, причем это проникновение будет тем более существенным, чем меньше размеры отверстия. При диаметре отверстия или ширине щели, сравнимых с длиной волны, приближение геометрической оптики становится совершенно неприменимым.
Качественно поведение света за преградой с отверстием может быть объяснено с помощью принципа Гюйгенса . Согласно принципу Гюйгенса каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времени. Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (Рис. 4.1.8).
Рис. 4.1.8. К принципу Гюйгенса
Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды.
4.1.8. Интерференция световых волн
Если в среде распространяются одновременно несколько электромагнитных волн, то волны просто накладываются друг на друга, не возмущая одна другую. Это утверждение, подкрепленное опытом, называется принципом суперпозиции.
В случае, когда колебания электрического и магнитного векторов в каждой из волн происходят так, что между соответственными векторами в разных волнах имеется постоянный во времени и в пространстве фазовый сдвиг, такие волны называются когерентными . Очевидно, что условие когерентности может существовать лишь для волн, которые имеют одинаковые частоты и, соответственно, длины волны.
При сложении когерентных волн возникает явление интерференции , заключающееся в том, что электромагнитные волны в одних точках пространства усиливают, а в других ослабляют друг друга.
Пусть две волны одинаковой частоты, распространяющиеся в одном направлении, возбуждают в некоторой точке пространства колебания:
| (4.1.83) |
Эти векторы можно представить как вращающиеся с частотой ω вокруг общего начала коор-динат. Поскольку сдвиг фаз различен, в какой-либо момент времени эти вектора займут различные положения (Рис. 4.1.9).
Рис. 4.1.9. К расчету интерференции волн
Используя теорему косинусов, получим амплитуду результирующего колебания:
| (4.1.84) |
Если сдвиг фаз между когерентными колебаниями равен нулю (волны — в фазе), то амплитуда результирующей волны максимальна и равна A = A1 + A2. Пусть амплитуды этих волн равны. В этом случае имеем амплитуду результирующей волны:
| (4.1.85) |
Если сдвиг фаз между когерентными колебаниями равен ±π (волны — в противофазе), то амплитуда результирующей волны минимальна и равна A = A1 — A2. Если амплитуды этих волн равны, то в этом случае они гасят друг друга:
| (4.1.86) |
Когерентные световые волны можно получить, разделив, например, с помощью зеркал волну, излучаемую одним источником, на две. Если заставить эти волны пройти разные пути, а затем наложить их друг на друга, будет наблюдаться интерференция. Пусть такое разделение происходит в точке О (Рис. 4.1.10).
Рис. 4.1.10. Образование когерентных волн
До точки Р первая волна пройдет в среде с показателем преломления n1 путь S1, вторая волна пройдет в среде с показателем преломления n2 путь S2. Если в точке О фаза колебания была равна ωt, то первая волна возбудит в точке Р колебание
| (4.1.87) |
а вторая волна — колебание
| (4.1.88) |
поскольку фазовые скорости волн в средах равны, соответственно: . Следовательно, разность фаз волн в точке Р будет равна:
| (4.1.89) |
Поскольку выполняется:
| (4.1.90) |
то, подставляя (4.1.90) в (4.1.8), для сдвига фаз имеем выражение:
| (4.1.91) |
где
| (4.1.92) |
есть величина, называемая оптической разностью хода и равная разности оптических длин проходимых волнами путей в средах с различными показателями преломления.
Из (4.1.91) следует, что если оптическая разность хода равна целому числу длин волн в вакууме:
| (4.1.93) |
то разность фаз оказывается кратной 2π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в фазе. Следовательно, (4.1.93) является условием интерференционного максимума.
Если Δ равна полуцелому числу длин волн в вакууме:
| (4.1.94) |
то разность фаз оказывается равной δ = ±(2m + 1)π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (4.1.94) является условием интерференционного минимума.
4.1.9. Дифракция световых волн
Дифракцией называется совокупность явлений, связанных с отклонениями от законов геометрической оптики. В частности, вследствие дифракции происходит огибание световыми волнами препятствий и проникновение света в область геометрической тени.
Между интерференцией и дифракцией нет существенного физического различия.
Свет, идущий от небольшого яркого источника через круглое отверстие (Рис. 4.1.11) должен по правилам геометрической оптики дать на экране резко ограниченный светлый кружок на темном фоне.
Рис. 4.1.11. Дифракция от круглого отверстия
Такая картина наблюдается при обычных условиях опыта. Но если расстояние от отверстия до экрана в несколько тысяч раз превосходит размеры отверстия, то образуется более сложная картина, которая состоит из совокупности светлых и темных концентрических колец.
Интересный случай дифракции осуществляется с помощью дифракционной решетки, которая представляет собой пластинку, на поверхности которой чередуются узкие параллельные прозрачные и непрозрачные полоски. Сумму ширины прозрачной и непрозрачной полосок называют периодом решетки. Пусть на решетку падает монохроматический свет с длиной волны λ (Рис. 4.1.12). Фронт волны параллелен плоскости решетки.
Рис. 4.1.12. Дифракционная решетка
Разности хода лучей, идущих от соответствующих точек отверстий, например от правых краев (точки А, А1, А2, . ), или от левых краев (точки В, В1, В2, . ) имеют одно и то же значение:
Для того, чтобы все пучки усиливали друг друга, необходимо, чтобы разность хода равнялась целому числу длин волн:
| (4.1.95) |
где m — целое число.
Это условие позволяет определить те значения углов φ и соответствующие направления, в которых будут наблюдаться максимумы света длины волны λ.
Для данной длины волны может наблюдаться несколько максимумов. Направление, соответствующее m = 0, есть φ = 0. Это — направление первоначального пучка. Соответствущий максимум носит название максимума нулевого порядка. При m = 1 имеем: sinφ1 = λ/d, при m = 1 имеем: sinφ’1 = λ/d, т.е. имеется два максимума первого порядка, расположенных симметрично по обеим сторонам от нулевого максимума. Аналогично располагаются максимумы второго, третьего и т.д. порядков.
Отсюда следует, что для волн разной длины λ положения максимумов нулевого порядка совпадают , а положения максимумов первого, второго и т.д. порядков различны: чем больше λ, тем больше соответствующие углы.
Если на решетку падает белый свет, то в плоскости экрана получается ряд цветных изображений щели. На месте нулевого максимума будет изображение щели в белом свете, а по обе стороны от него развернутся цветные полосы от фиолетового к красному концу.
Чем больше общий размер решетки, т.е. чем больше полосок она содержит, тем выше ее качество: увеличение числа полосок увеличивает количество пропускаемого решеткой света (максимумы становятся ярче), и улучшает разрешение близких волн (максимумы становятся резче).
Зная период дифракционной решетки, ее можно использовать для определения длины световой волны, измерив величину угла φ, определяющего положение максимума данного порядка. В этом случае имеем:
| (4.1.96) |
Измерение длины световой волны с помощью дифракционной решетки принадлежит к числу наиболее точных методов.
4.1.10. Поляризация световых волн
Поляризованным называется свет, в котором направления колебаний электрического и магнитного векторов упорядочены каким-либо образом. В естественном свете колебания происходят в различных направлениях, быстро и беспорядочно сменяя друг друга.
Различают свет эллиптически поляризованный, поляризованный по кругу, плоскополяризованный. В случае эллиптической или круговой поляризаций электрический и магнитный векторы вращаются в пространстве с частотой, равной частоте волны, причем концы этих векторов описывают либо эллипс, либо круг. Вращение может происходить как по, так и против часовой стрелки. Если вектор вращается в пространстве как правый винт, то поляризацию называют правой, и левой — если вектор вращается в пространстве как левый винт.
Важный частный случай — плоская поляризация. В этом случае вектор электрического поля колеблется в плоскости, проходящей через направление распространения волны и этот вектор. Такую плоскость называют плоскостью колебаний . Вектор магнитного поля колеблется в плоскости, также проходящей через направление распространения волны и этот вектор, но данная плоскость — плоскость поляризации — составляет с плоскостью колебаний прямой угол (Рис. 4.1.13).
Рис. 4.1.13. Структура плоскополяризованной световой волны
Плоскополяризованный свет можно получить из естественного с помощью устройств, которые называются поляризаторами . Эти устройства свободно пропускают волны с колебаниями, плоскость которых совпадает с плоскостью пропускания поляризатора, и задерживают все другие волны.
Пусть на поляризатор падает плоскополяризованный свет амплитуды А0 и интенсивности I0. Сквозь устройство пройдет составляющая колебания с амплитудой А|| = А0cosφ, где угол φ — угол между плоскостью колебаний падающего света и плоскостью пропускания поляризатора (Рис. 4.1.14).
Рис. 4.1.14. Прохождение плоскополяризованного света через поляризатор
Следовательно, интенсивность прошедшего света определяется выражением:
| (4.1.97) |
Это соотношение носит название закона Малюса.
Пусть на пути естественного луча стоят два поляризатора, плоскости пропускания которых составляют угол φ. Из первого поляризатора выйдет плоскополяризованный свет, интенсивность которого I0 составит половину интенсивности естественного неполяризованного света Iест. Используя закон Малюса, получаем:
| (4.1.98) |
Максимальная интенсивность получается при φ = 0 (плоскости пропускания поляризаторов параллельны). При φ = 90° интенсивность равна нулю — скрещенные поляризаторы не пропускают свет.
4.1.11. Вращение плоскости
поляризации световых волн
Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света. К числу таких веществ относятся кристаллы кварц, киноварь и др, некоторые жидкости (скипидар, никотин), растворы оптически активных веществ в оптически неактивных растворителях (водные растворы сахара, винной кислоты и др.)
Угол поворота плоскости поляризации в твердых веществах пропорционален пути l, пройденному лучом в кристалле:
| (4.1.99) |
где α — постоянная оптического вращения, различная для разных веществ.
В растворах угол поворота плоскости поляризации пропорционален пути l, пройденному светом в растворе и концентрации с активного вещества:
| (4.1.100) |
Здесь [α] — удельная постоянная вращения.
В зависимости от направления вращения вещества подразделяются на право- и левовращающие. Существуют правый и левый кварц, правый и левый сахар и т.д. Молекулы или кристаллы одной модификации являются зеркальным отражением молекул или кристаллов другой модификации.
Если между двумя скрещенными поляризаторами поместить оптически активное вещество, то поле зрения просветляется. Чтобы снова затемнить его, надо повернуть один из поляризаторов на угол, определяемый соотношениями (4.1.99) или (4.11.100). Таким методом можно измерить концентрацию активного вещества в растворе, в частности, концентрацию сахара.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Первое уравнение Максвелла.
Первое уравнение Максвелла — это обобщение закона Ампера и Био-Саварра для токов смещения. Звучит следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.
В современном обозначении записывается
Т.о. физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области(токами смещения).
Это означает, что циркуляция вектора 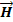

Уравнение 1.12 называют первым уравнением Максвелла в интегральной форме.
Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:
Применим уравнение 1.13 к левой части уравнения 1.12. Получим
Уравнение 1.14 справедливо, если равны подынтегральные функции, то есть
Уравнение 1.15 есть первое уравнение Максвелла в дифференциальной форме.
Для изотропных сред
Подставим в 1.15
Дифференциальная форма первого уравнения Максвелла используется в том случае, когда производные поля по координатам пространства непрерывны. Интегральная форма 1.12 такого ограничения не имеет.
§1.3. Второе уравнение Максвелла.
Второе уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве
где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.
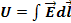
Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.
Получим второе уравнение Максвелла в интегральной форме
Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.
Воспользуемся уравнением Стокса 1.13, преобразуем левую часть уравнения 1.19:
Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.
http://www.kgau.ru/distance/2013/et4/001/04_01.htm
http://helpiks.org/6-65047.html