Виды нелинейных дифференциальных уравнений 1-го порядка
Описание: Дифференциальное уравнение уравнение связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию её производные и независимые переменные; однако не любое уравнение содержащее производные неизвестной функции является дифференциальным уравнением. Нелинейное дифференциальное уравнение дифференциальное уравнение обыкновенное или с частными производными в которое по крайней мере одна.
Дата добавления: 2015-01-14
Размер файла: 163.25 KB
Работу скачали: 139 чел.
Поделитесь работой в социальных сетях
Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск
ПГУ им. Т.Г. Шевченко
Виды нелинейных дифференциальных уравнений 1-го порядка
студент 211 группы
Бирт Игорь Андреевич
Тирасполь 2014 год
1. Введение 3 стр.
2. Виды дифференциальных уравнений 4 стр.
3. Практическая часть 8 стр.
4. Литература 20 стр.
Дифференциальное уравнение уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.
Порядок дифференциального уравнения наибольший порядок производных, входящих в него.
Процесс решения дифференциального уравнения называется интегрированием.
Все дифференциальные уравнения можно разделить на линейные и не линейные.
Нелинейное дифференциальное уравнение — дифференциальное уравнение ( обыкновенное или с частными производными ), в к ото рое по крайней мере о дна из производных неизвестной функции ( включая и производную нулевого порядка — саму неизвестную функцию ) входит нелинейно .
Иногда под Н.Д.У. понимается наиболее общее уравнение определенного вида. Напр ., нелинейнымобыкновенным дифференциальным уравнением 1 — го порядка наз . уравнение с произвольной
функцией при этом линейное обыкновенное дифференциальное уравнение 1-го порядка соответствует частному случаю
Н . д . у . с частными производными 1-го порядка для неизвестной функции z
от независимых переменных имеет вид:
где F — произвольная функция своих аргументов ;
Виды нелинейных дифференциальных уравнений 1-го порядка:
Уравнения с разделенными переменными
Уравнение в полных дифференциалах
Существует такая функция u(x, y) , что
Общий интеграл уравнения в полных дифференциалах u(x, y) = C.
Функция u может быть представлена в виде
где P(x, y) , Q(x, y) — однородные функции одной и той же степени
Подстановка y = ux , dy = xdu + udx переводит однородное уравнение в линейное относительно функции u :
1. Если прямые и пересекаются в точке
( x 0 ; y 0 ), то замена приводит его к однородному уравнению
2. Если прямые и параллельны, то замена приводит к уравнению с разделяющимися переменными
Подстановкой сводится к линейному
Если известно какое-либо из решений , то уравнение сводится к
Дифференцируя по x и полагая y’ = p , приходим к линейному уравнению относительно x как функции p :
— частный случай уравнения Лагранжа.
Решить дифференциальное уравнение
Данное уравнение является простейшим уравнением Риккати с постоянными коэффициентами. Переменные x, y здесь легко разделяются, так что общее решение уравнения определяется в следующем виде:
Решить уравнение Риккати
Будем искать частное решение в форме:
Подставляя это в уравнение, находим:
Получаем квадратное уравнение для c:
Мы можем выбрать любое значение c. Например, пусть c = 2. Теперь, когда частное решение известно, сделаем замену:
Снова подставим это в исходное уравнение Риккати:
Как видно, мы получили уравнение Бернулли с параметром m = 2. Сделаем еще одну замену:
Разделим уравнение Бернулли на z2 (полагая, что z ≠ 0) и запишем его через переменную v:
Последнее уравнение является линейным и легко решается с помощью интегрирующего множителя:
Общее решение линейного уравнения определяется функцией
Теперь мы будем последовательно возвращаться к предыдущим переменным. Так как z = 1/v, то общее решение для z записывается следующим образом:
Можно переименовать константу: 3C = C1 и записать ответ в виде
где C1 − произвольное действительное число.
Найти все решения дифференциального уравнения
Данное уравнение является уравнением Бернулли с дробным параметром
m = 1/2. Его можно свести к линейному дифференциальному уравнению с помощью замены
Производная новой функции z ( x ) будет равна
Разделим исходное уравнение Бернулли на
Аналогично другим примерам на этой веб-странице, корень y = 0 также является тривиальным решением дифференциального уравнения. Поэтому можно записать:
Заменяя y на z , находим:
Итак, мы имеем линейное уравнение для функции z ( x ). Интегрирующий множитель здесь будет равен
Выберем в качестве интегрирующего множителя функцию u ( x ) = x . Можно проверить, что после умножения на u ( x ) левая часть уравнения будет представлять собой производную произведения z ( x ) u ( x ):
Тогда общее решение линейного дифференциального уравнения будет определяться выражением:
Возвращаясь к исходной функции y ( x ), записываем решение в неявной форме:
Итак, полный ответ имеет вид:
Уравнения с разделяющимися переменными
Найти все решения дифференциального уравнения
Преобразуем уравнение следующим образом:
Очевидно, что деление на e y не приводит к потере решения, поскольку e y > 0. После интегрирования получаем
Данный ответ можно выразить в явном виде:
В последнем выражении предполагается, что константа C > 0, чтобы удовлетворить области определения логарифмической функции.
Найти частное решение уравнения, при
Перепишем уравнение в следующем виде:
Разделим обе части на 1 + e x :
Поскольку 1 + e x > 0, то при делении мы не потеряли никаких решений. Интегрируем полученное уравнение:
Теперь найдем константу C из начального условия y(0) = 0.
Следовательно, окончательный ответ имеет вид:
Найти общее и особое решения дифференциального уравнения
Полагая y’ = p, его можно записать в виде
Продифференцировав по переменной x, находим:
Заменим dy на pdx:
Приравнивая первый множитель к нулю, получаем:
Теперь подставим это во второе уравнение:
В результате получаем общее решение заданного уравнения Клеро. Графически, это решение представляется в виде однопараметрического семейства прямых. Приравнивая нулю второй сомножитель, находим еще одно решение:
Это уравнение соответствует особому решению дифференциального уравнения и в параметрической форме записывается как
Исключая p из системы, получаем следующее уравнение интегральной кривой:
С геометрической точки зрения, парабола
является огибающей семейства прямых, определяемых общим решением.
Найти общее и особое решения дифференциального уравнения
Введем параметр y’ = p:
Дифференцируя обе части уравнения по переменной x, получаем:
Поскольку dy = pdx, то можно записать:
Рассмотрим случай dp = 0. Тогда p = C. Подставляя это в уравнение, находим общее решение:
Графически это решение соответствует однопараметрическому семейству прямых линий.
Второй случай описывается уравнением
Найдем соответствующее параметрическое выражение для y:
Параметр p можно исключить из формул для x и y. Возводя последние уравнения в квадрат и складывая их, получаем:
Полученное выражение является уравнением окружности радиусом 1, расположенным в начале координат. Таким образом, особое решение представляется единичной окружностью в плоскости xy, которая является огибающей для семейства прямых линий.
- Н.С. Пискунов «Дифференциальное и интегральное исчисление», том второй, издательство «Наука», Москва 1985
- В. Ф. Зайцев, А. Д. Полянин. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001.
- К.Н. Лунгу, В.П. Норин и др. «Сборник задач по высшей математике», второй курс, Москва: Айрис-пресс, 2007
- Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.
- Источники информации в интернете.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
Примеры.
Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.
1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:
где dx/dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)
2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м 3 воды. Если чистая вода вливается в емкость со скоростью 1 м 3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м 3 раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или
3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2 x/dt 2 ) пропорционально силе:
Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.
4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то
где T – температура кофе в момент времени t.
5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:
где члены —ax и —by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)
После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.
Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.
Решения дифференциальных уравнений.
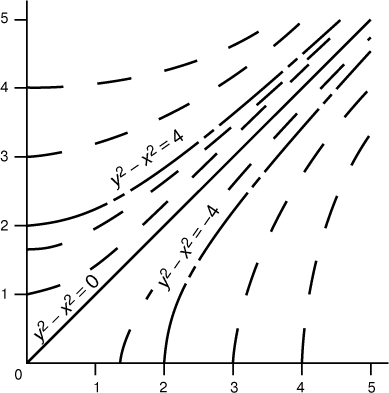
Дифференциальному уравнению, например dy/dx = x/y, удовлетворяет не число, а функция, в данном конкретном случае такая, что ее график в любой точке, например в точке с координатами (2,3), имеет касательную с угловым коэффициентом, равным отношению координат (в нашем примере 2/3). В этом нетрудно убедиться, если построить большое число точек и от каждой отложить короткий отрезок с соответствующим наклоном. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Если точек и отрезков достаточно много, то мы можем приближенно наметить ход кривых-решений (три такие кривые показаны на рис. 1). Существует ровно одна кривая-решение, проходящая через каждую точку с y № 0. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее – целое их семейство. Решить дифференциальное уравнение – это значит найти либо его частное, либо общее решение. В рассматриваемом нами примере общее решение имеет вид y 2 – x 2 = c, где c – любое число; частное решение, проходящее через точку (1,1), имеет вид y = x и получается при c = 0; частное решение, проходящее через точку (2,1), имеет вид y 2 – x 2 = 3. Условие, требующее, чтобы кривая-решение проходила, например, через точку (2,1), называется начальным условием (так как задает начальную точку на кривой-решении).
Можно показать, что в примере (1) общее решение имеет вид x = ce –kt , где c – постоянная, которую можно определить, например, указав количество вещества при t = 0. Уравнение из примера (2) – частный случай уравнения из примера (1), соответствующий k = 1/100. Начальное условие x = 10 при t = 0 дает частное решение x = 10e –t/100 . Уравнение из примера (4) имеет общее решение T = 70 + ce –kt и частное решение 70 + 130 –kt ; чтобы определить значение k, необходимы дополнительные данные.
Дифференциальное уравнение dy/dx = x/y называется уравнением первого порядка, так как содержит первую производную (порядком дифференциального уравнения принято считать порядок входящей в него самой старшей производной). У большинства (хотя и не у всех) возникающих на практике дифференциальных уравнений первого рода через каждую точку проходит только одна кривая-решение.
Существует несколько важных типов дифференциальных уравнений первого порядка, допускающих решения в виде формул, содержащих только элементарные функции – степени, экспоненты, логарифмы, синусы и косинусы и т.д. К числу таких уравнений относятся следующие.
Уравнения с разделяющимися переменными.
Уравнения вида dy/dx = f(x)/g(y) можно решить, записав его в дифференциалах g(y)dy = f(x)dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy/dx = x/y имеем f(x) = x, g(y) = y. Записав его в виде ydy = xdx и проинтегрировав, получим y 2 = x 2 + c. К уравнениям с разделяющимися переменными относятся уравнения из примеров (1), (2), (4) (их можно решить описанным выше способом).
Уравнения в полных дифференциалах.
Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N – две заданные функции, то его можно представить как M(x,y)dx – N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d(y 2 – x 2 ) = 0. Функция F(x,y) в этом случае равна (1/2)(y 2 – x 2 ); некоторые из ее линий постоянного уровня представлены на рис. 1.
Линейные уравнения.
Линейные уравнения – это уравнения «первой степени» – неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy/dx + p(x) = q(x), где p(x) и q(x) – функции, зависящие только от x. Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов.
Уравнения старших порядков.
Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Таково, например, уравнение простого гармонического движения из примера (3), md 2 x/dt 2 = –kx. Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Например, рассмотрим уравнение md 2 x/dt 2 = –kx и потребуем, чтобы y(0) = y(1) = 0. Функция y є 0 заведомо является решением, но если 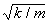
Уравнение простого гармонического движения служит примером важного класса уравнений, а именно: линейных дифференциальных уравнений с постоянными коэффициентами. Более общий пример (также второго порядка) – уравнение
где a и b – заданные постоянные, f(x) – заданная функция. Такие уравнения можно решать различными способами, например, с помощью интегрального преобразования Лапласа. То же можно сказать и о линейных уравнениях более высоких порядков с постоянными коэффициентами. Не малую роль играют также и линейные уравнения с переменными коэффициентами.
Нелинейные дифференциальные уравнения.
Уравнения, содержащие неизвестные функции и их производные в степени выше первой или каким-либо более сложным образом, называются нелинейными. В последние годы они привлекают все большее внимание. Дело в том, что физические уравнения обычно линейны лишь в первом приближении; дальнейшее и более точное исследование, как правило, требует использования нелинейных уравнений. Кроме того, многие задачи нелинейны по своей сути. Так как решения нелинейных уравнений зачастую очень сложны и их трудно представить простыми формулами, значительная часть современной теории посвящена качественному анализу их поведения, т.е. разработке методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограниченны, или имеют периодический характер, или определенным образом зависят от коэффициентов.
Приближенные решения дифференциальных уравнений могут быть найдены в численном виде, но для этого требуется много времени. С появлением быстродействующих компьютеров это время сильно сократилось, что открыло новые возможности численного решения многих, ранее не поддававшихся такому решению, задач.
Теоремы существования.
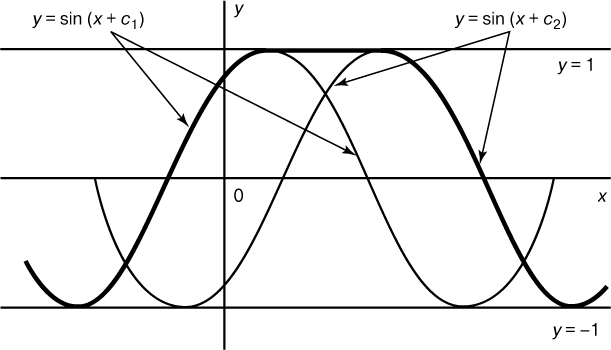
Теоремой существования называется теорема, утверждающая, что при определенных условиях данное дифференциальное уравнение имеет решение. Встречаются дифференциальные уравнения, не имеющие решений или имеющие их больше, чем ожидается. Назначение теоремы существования – убедить нас в том, что у данного уравнения действительно есть решение, а чаще всего заверить, что оно имеет ровно одно решение требуемого типа. Например, уже встречавшееся нам уравнение dy/dx = –2y имеет ровно одно решение, проходящее через каждую точку плоскости (x,y), а так как одно такое решение мы уже нашли, то тем самым полностью решили это уравнение. С другой стороны, уравнение (dy/dx) 2 = 1 – y 2 имеет много решений. Среди них прямые y = 1, y = –1 и кривые y = sin(x + c). Решение может состоять из нескольких отрезков этих прямых и кривых, переходящих друг в друга в точках касания (рис. 2).
Дифференциальные уравнения в частных производных.
Обыкновенное дифференциальное уравнение – это некоторое утверждение о производной неизвестной функции одной переменной. Дифференциальное уравнение в частных производных содержит функцию двух или более переменных и производные от этой функции по крайней мере по двум различных переменным.
В физике примерами таких уравнений являются уравнение Лапласа
где, согласно одной из возможных интерпретаций, u – температура в плоской области, точки которой задаются координатами x и y; уравнение теплопроводности
где t – время, x – расстояние от одного из концов однородного стержня, по которому распространяется тепловой поток; и волновое уравнение
где t – снова время, x и y – координаты точки колеблющейся струны.
Решая дифференциальные уравнения в частных производных, обычно не стремятся найти общее решение, поскольку оно скорее всего окажется слишком общим, чтобы быть полезным. Если решение обыкновенного дифференциального уравнения определяется заданием условий в одной или нескольких точках; то решение дифференциального уравнения в частных производных обычно определяется заданием условий на одной или нескольких кривых. Например, решение уравнения Лапласа может быть найдено в точке (x, y) внутри круга, если значения u заданы в каждой точке ограничивающей окружности. Поскольку проблемы с более чем одной переменной в физике являются скорее правилом, чем исключением, легко представить, сколь обширен предмет теории дифференциальных уравнений в частных производных.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1982
Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984
Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М., 1986
Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение

Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или 
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение 


Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или 
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение 

Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная 
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной 
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение 
которые проходят через начало координат (рис. 1).
Уравнение 
Если задано начальное условие 
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части: 
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение: 
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим: 


Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,

Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем 
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим 
Интегрируя, получим



Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:

Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену 

Тогда уравнение (7.10) запишется в виде 
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле

то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение 
то есть 

После интегрирования получим 
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить 
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению


Отделяя переменные, найдем




Возвращаясь к переменной y, получим общее решение: 
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем 
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16): 
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:

При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение 
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: 

Выражение, стоящее в скобках, приравниваем к нулю, имеем

Отделим переменные, домножив обе части уравнения на 

После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения 
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда 
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение 
Дифференциальное уравнение Бернулли
Определение. Уравнения вида


называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену: 
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим: 
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. 
Сделаем замену 
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда 
Проинтегрировав правую часть этого уравнения по частям, получим 
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную 


Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь 
Число 
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых 
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные 

Умножая обе части уравнения (3) на некоторую функцию 
где 


Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), 




- Существует производная
для всех значений
из интервала
(Отсюда следует, что решение
представляет собою функцию, непрерывную ею всей области определения).
- Функция
обращает уравнение (2) в тождество:
справедливое для всех значений 





Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения 
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале 
справедливое при всех значениях
Пример 2.
Функция 

Пример 3.
является решением уравнения
в интервале
Иногда функцию 
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила 
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила

функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:

где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:

Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38): 
Заменим производные


Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем 
Продолжая дальше таким образом, получим 
В результате получаем следующую систему уравнений:

Из первых (n-1) уравнений определим y2, y3, . yn:

и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим


Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему 
когда заданы начальные условия 
Решение. Дифференцируем по x первое уравнение, имеем: 



Из первого уравнения системы найдем 

Общим решением этого уравнения является

и тогда 
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:

где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:

Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:

Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:

Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем 


Откуда 


Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда 
Получим второй решение системы: 
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:


Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:

где 

Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:

Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/DIFFERENTSIALNIE_URAVNENIYA.html
http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/




















































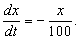
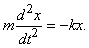
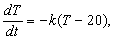
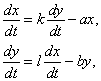
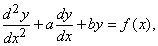
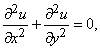
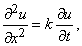
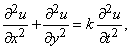


































 для всех значений
для всех значений  из интервала
из интервала  (Отсюда следует, что решение
(Отсюда следует, что решение  представляет собою функцию, непрерывную ею всей области определения).
представляет собою функцию, непрерывную ею всей области определения). обращает уравнение (2) в тождество:
обращает уравнение (2) в тождество: 


































