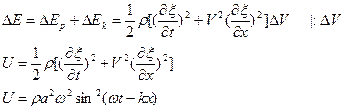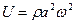Гармоническая волна
Волна называется гармонической, если она описывается функцией,
ψ(t,х) = А cos(ωt-kx + a), (11.4)
где А — амплитуда волны; ω — частота; к — волновое число; а — начальная фаза;
— фаза волны. Функцию (11.4) можно привести к виду (11.2):
видно, что скорость гармонической волны связана с частотой и волновым числом соотношением
Для того чтобы получить зависимость величины ψ от времени t, которая описывает ее изменения со временем в данной точке пространства, следует положить в формуле (11.4) х = const. Так как функция (11.4) при х = const описывает гармонические колебания, говорят, что гармоническая волна создает в произвольной точке пространства гармонические колебания.
T=2π/ω — период волны, а (11.7)
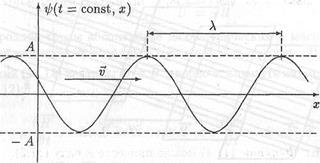
— длиной волны. Если фаза (11.5) волны получит приращение 2π, то, значение функции (11.4) останется прежним. Поэтому при х= const функция (11.4) принимает одно и то же значение для всех моментов времени, которые отличаются одно от другого на пТ, где п — целое число; а при t = const значения функции (11.4) в различных точках пространства совпадают, если координаты этих точек отличаются друг от друга на пλ. График зависимости величины ψ(t,х) от координаты х при t = const для случая, когда вдоль оси х распространяется гармоническая волна, показан на рис. 11.2.
Рис. 11.2. Гармоническая волна
11.3. Волны впространстве
Пусть физическая величина ψ распределена в пространстве, и это распределение меняется со временем. Говорят, что функция ψ = ψ(t,r) описывает волну, распространяющуюся в пространстве, если она удовлетворяет уравнению
 |
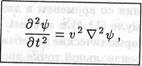Волна называется плоской, если существует такая система декартовых координат, в которой функция ψ зависит только от одной из координат. Если этой координатой является х, то уравнение (11.9) сводится к (11.1). В произвольной прямоугольной системе декартовых координат плоская гармоническая волна описывается функцией
ψ(t,r) = A cos(ωt-kr + a), (11.10
 |
где вектор кназывается волновым. В том, что эта функция является решением уравнения (11.9), нетрудно убедиться непосредственной подстановкой.
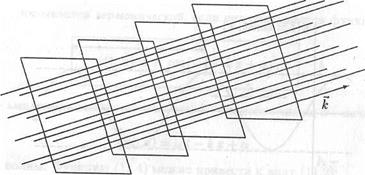
Рис. 11.3. Фазовые поверхности и лучи, вдоль которых распространяется в пространстве плоская волна
φ(t, r) = ωt –kr+a
называется фазой плоской волны. Поверхность
φ(t = const, r) = const, или kr= const
постоянной фазы (11.11) является плоскостью, к которой вектор кперпендикулярен. Такие поверхности называют фазовыми, или волновыми, а линии, перпендикулярные к фазовым поверхностям, называют лучами. Для плоской волны лучами являются прямые, параллельные волновому вектору. Этот вектор указывает направление распространения волны, а его модуль (волновое число), частота и скорость волны связаны соотношением (11.6). На рис. 11.3 изображены фазовые поверхности и лучи плоской волны.
11.4. Плоские электромагнитные волны *
Рассмотрим электромагнитное поле в пространстве, заполненном однородным диэлектриком, в котором отсутствуют свободные заряды и электрические токи, т.е. объемная плотность связанных зарядов и плотность тока равны нулю:
ρ=0, j=0
В таком случае уравнения Максвелла (10.1) — (10.4) принимают вид
(11.12)
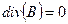
D =εE, В =μH. (10.13)
Для однородной среды абсолютные диэлектрическая и магнитная проницаемости вещества постоянны: ε = const и μ = const. При помощи
соотношений (11.13) векторы D и В удобно исключить из системы уравнений (11.12):
→ divE=0
→ 
→ 
→divH=0
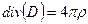
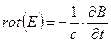
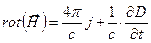
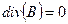
Пусть векторы Е и Н зависят только от t и у:
Покажем, что эти функции могут быть решениями уравнений (11.14), а также, что среди решений уравнений (11.14) такого вида есть функции, описывающие плоские электромагнитные волны, распространяющиеся вдоль оси у.
Вычислим ротор и дивергенцию вектора E(t, у)
rot E =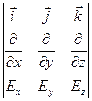 
= 
+ 
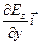
div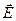 
= 
С учетом этих формул подстановка векторов (11.15) в равенства (11.14) приводит к системе уравнений
= 
(11.16)
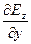
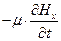
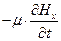
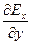
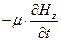
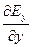
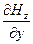
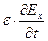
0= (11.17)
— 
= 
(11.18)
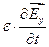
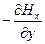
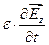
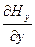
=0 (11.19)
= 
(11.20)
0= 
(11.21)
= 
(11.22)
=0 (11.23)
Из уравнений (11.19) и (11.21) следует, что Еy = const. Очевидно, что постоянное электрическое поле в электромагнитной волне отсутствует. Поэтому положим
Аналогично, уравнения (11.17) и (11.23) приводят к равенству
Оставшиеся неиспользованными уравнения можно разделить на две независимые системы. Первая состоит из уравнений (11.16) и (11.22) для функций Ez и Нх, а вторая — из уравнений (11.18) и (11.20) для функций Ех и Нг. Выпишем уравнения первой системы:
=
=
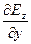
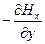
Исключим Нх из этой системы. Для этого продифференцируем уравнение (11.16) по у, а уравнение (11.22) — по i. После несложных преобразований придем к уравнению
= 
; (16.26)
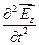
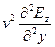
v=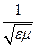 
(11.27)
Уравнение (11.26) есть волновое уравнение. Одно из его решений, описывающих гармоническую волну, имеет вид
где Em — амплитуда волны. Эта волна распространяется вдоль оси у в сторону возрастания у.
также является решением волнового уравнения (11.26). Эта функция есть плоская гармоническая волна, распространяющаяся вдоль оси у в сторону убывания у.
Найдем функцию Hx(t,y), соответствующую функции (11.28). Для этого подставим выражение (11.28) в уравнения (11.16) и (11.22). Получим:
= -( кЕm/μ)sin(ωt- к у + а),
= ωεEm sin(ωt- ky +a)
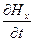
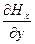
Отсюда с учетом соотношений (11.6) и (11.27) найдем, что
Нт =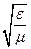 
Ет (11.30)
В частном случае система уравнений (11.18) и (11.20) имеют нулевое
Нетрудно проверить, что функции
при условии (11.30) также являются решениями системы уравнений (11.18) и (11.20).
Итак, найдены решения уравнений Максвелла в виде плоских гармонических волн, распространяющихся вдоль оси у. Решениями уравнений Максвелла могут быть не только плоские гармонические волны. Вдоль оси у могут распространяться электромагнитные волны более сложной формы. Например, это может быть произвольная суперпозиция плоских гармонических волн. Для всех этих волн справедливы равенства (11.24) и (11.25). Вообще все электромагнитные волны обладают таким свойством. Проекции векторов Е и H на направление, вдоль которого распространяется электромагнитная волна всегда равны нулю. Это свойство называют поперечностъю электромагнитных волн.
Дата добавления: 2015-06-12 ; просмотров: 3862 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Плоская гармоническая волна представлена уравнением
| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Плоская гармоническая волна. Амплитуда, частота, фаза, длина волны. Фазовая скорость волны. Сферические волныВиды Механических волн. Упругие волны в стержнях. Волновое уравнение. 1)Продольные – частицы среды колеблются вдоль направления распространения волны. 2)Поперечные – частицы колеблются перпендикулярно направлению распространения волны. Уравнение любой волны – есть решение дифференциального уравнения, называемого волновым: Если в какой-либо сплошной упругой среде возникает механическая деформация, то благодаря упругим силам, изменение этой деформации может иметь колебательный характер. Эти колебания будут распространяться с конечной скоростью от данного участка среды к другим участкам. Волной называется процесс распространения колебаний в среде. Для затухающей монохроматической плоской волны, бегущей в направлении Х
X – координата точки равновесия частицы Т – период колебаний W – Круговая частота V – Фазовая скорость волны Рассмотрим элемент стержня dx, заключенный между поперечными сечениями стержня в точках x и x+dx
При распространении вдоль стержня (по Ох) продольной волны в любом его сечении возникает напряжении. Сила, действующая на dx
С учетом малости dx
Получаем волновое уравнение:
Плоская гармоническая волна. Амплитуда, частота, фаза, длина волны. Фазовая скорость волны. Сферические волны. Уравнение плоской колебательной волны:
X – координата точки равновесия частицы Т – период колебаний W – круговая частота V – фазовая скорость волны Фазовая скорость – скорость распространения волны (скорость перемещения фазы) Длина Волны λ – расстояние, на которое фронт волны перемещается за период.
Амплитуда – максимальное отклонение частицы от положения равновесия. Частота— число полных колебаний или циклов волны, совершенных в единицу времени. В случае, когда скорость распространения волны во всех направлениях будет одна и та же, волна будет сферической
A – постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице. В случае сферической волны амплитуда колебаний не считается постоянной, даже если энергия волны не поглощается средой. 3)Энергия упругой волны. Объемная плотность энергии волны. Вектор Умова – вектор плотности потока энергии. Выделим в среде, в которой распространяется продольная волна, элементарный объем ∆V, настолько малый, чтобы деформации и скорости движения во всех точках можно было считать одинаковыми,
Для поперечной волны аналогично Плотностью энергии в каждый момент времени в разных точках пространства различна Среднее по времени значение плотности в каждой точке
Потоком энергии Ф через поверхность – это количество энергии, пере волной через эту поверхность в единицу времени. Вектор плотности потока энергии Вектор, как и плотность энергии U, различен в разных точках пространства. источники: http://ens.tpu.ru/POSOBIE_FIS_KUSN/%D0%9A%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F%20%D0%B8%20%D0%B2%D0%BE%D0%BB%D0%BD%D1%8B.%20%D0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F%20%D0%B8%20%D0%B2%D0%BE%D0%BB%D0%BD%D0%BE%D0%B2%D0%B0%D1%8F%20%D0%BE%D0%BF%D1%82%D0%B8%D0%BA%D0%B0/05-2.htm http://lektsii.org/6-82380.html |
.
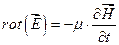
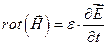
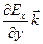
. Пусть колебание точек, лежащих в плоскости 
, имеет вид (при начальной фазе 
)
.
,
. Это будет, если энергия волны не поглощается средой.
, или 
.
.
, или в векторной форме:
,
– волновой вектор, 
– нормаль к волновой поверхности.
, то 
. Отсюда 
. Тогда уравнение плоской волны запишется так:
.
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу 
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 
. Следовательно, уравнение сферической волны:
, или 
,
, амплитуда стремится к бесконечности. То, что амплитуда колебаний 
, следует из рассмотрения энергии, переносимой волной.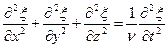
V – Скорость распространения волны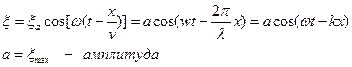
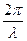— волновое число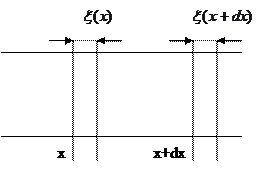
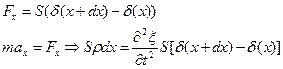
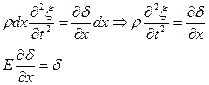
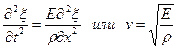
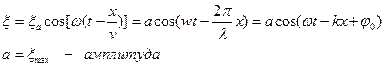
— начальная фаза
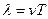
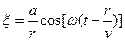
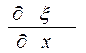и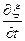 
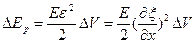— потенциальная энергия упругой деформации
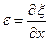— отношение удлинения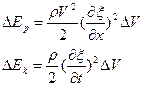
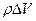— масса объема
