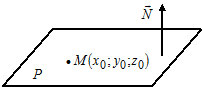Плоскость бета задана уравнением 3x y 2z 1

Угол между плоскостями. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти угол между плоскостями. Дается подробное решение с пояснениями. Для вычисления угла между плоскостями, введите элементы уравнения плоскостей в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Угол между плоскостями − теория

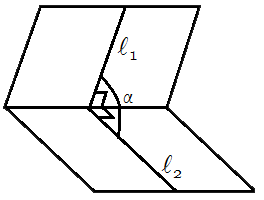
Пусть заданы две плоскости α и β общими уравнениями

Из определения скалярного произведения, имеем

.

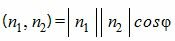(3)

Тогда из (3) можно найти косинус угла между нормальными векторами n₁ и n₂:

.

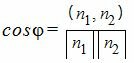(4)

Учитывая, что (n₁, n₂)=A₁A₂+B₁B₂+C₁C₂ и длины векторов |n₁|= и |n₂|=выражение (4) можно записать так:

.

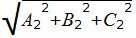
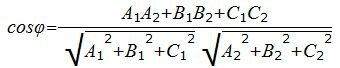(5)

Таким образом косинус угла между нормальными векторами и, следовательно, косинус угла между плоскостями α и β определяется формулой (5). Далее можно найти угол φ с помощью функции arccos.

Отметим, что пересекающиеся плоскости образую два угла. Другой угол можно найти так: φ‘=180−φ.

Онлайн калькулятор. Угол между плоскостями.

Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между плоскостями.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между плоскостями и закрепить пройденный материал.

Найти угол между плоскостями

Уравнение 1-ой плоскости:

Уравнение 2-ой плоскости:

Ввод данных в калькулятор для вычисления угла между плоскостями

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления угла между плоскостями

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Угол между плоскостями

Двугранный угол между плоскостями равен углу образованному их нормальными векторами.

Если заданы уравнения плоскостей A₁ x + B₁ y + C₁ z + D₁ = 0 и A₂ x + B₂ y + C₂ z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Аналитическая геометрия
• Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения плоскости:

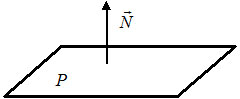
1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $\overline=(A, B, C) -$ нормальный вектор плоскости $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline=(A, B, C).$ Вектор $\overline N$ называется нормальным вектором плоскости.

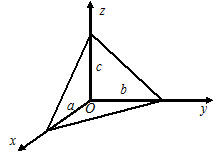
4) $\beginx-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&x_2-x_1&x_3-x_1\end=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$

5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ нормальное уравнение плоскости, где $\cos\alpha, \cos\beta$ и $\cos\gamma -$ направляющие косинусы нормального вектора $\overline,$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac<\sqrt>.$

Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Примеры:

2.180.

а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $\rho(P, P’).$

Решение.

Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $\overline=(-2, 1, -1).$

Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline=(A, B, C).$

Ответ: $-2x+y-z+2=0.$

2.181.

а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$

Решение.

Из уравнения плоскости $P,$ находим ее нормальный вектор $\overline=(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)\in P’$ такую, что что $\overline||\overline.$

Поскольку $z_N=0,$ то есть вектор $N\in XoY,$ то $z_=0.$

Мы нашли точку $M_3=(2, 1, 0).$

Так как точка $M_1\in P’,$ то и $M_3\in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$

$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow-z+y-2+z+x-1=0\Rightarrow x+y-3=0.$

2.182.

а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$

Решение.

Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:

Таким образом $\overline=[a_1, a_2]=(1, -2, 1).$

Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $\overline N=(1, -2, 1):$

Ответ: $x-2y+z=0.$

2.183.

а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$

Решение.

Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $\overline,$ параллельного вектору $a,$ точка $M_3\in P.$

Пусть $M_3=(x, y, z).$ Тогда $\overline=(x-1, y-2, z).$ Так как $\overline||a,$ то $\frac>=\frac>=\frac>.$ $y_a=0,$ то есть вектор $a\in XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_=y-2=0\Rightarrow y=2.$

Из условия параллельности векторов имеем $\frac<3>=\frac<1>.$ Пусть $x=4,$ тогда $z=1.$

Мы получили точку $M_3=(4, 2, 1).$

Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$

$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$

$\Rightarrow -x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0.$

2.184.

а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$

Решение.

Воспользуемся формулой (4):

$\Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0\Rightarrow x+y-3=0.$