Плоскость и ее уравнения угол между плоскостями

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

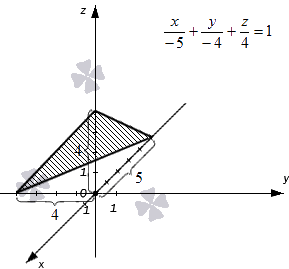
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Уравнения плоскости. Угол между двумя плоскостями

Плоскость, наряду с точкой и прямой линией, является базовым геометрическим элементом. С его использованием строятся многие фигуры в пространственной геометрии. В данной статье рассмотрим подробнее вопрос о том, как между двумя плоскостями угол найти.

Понятие

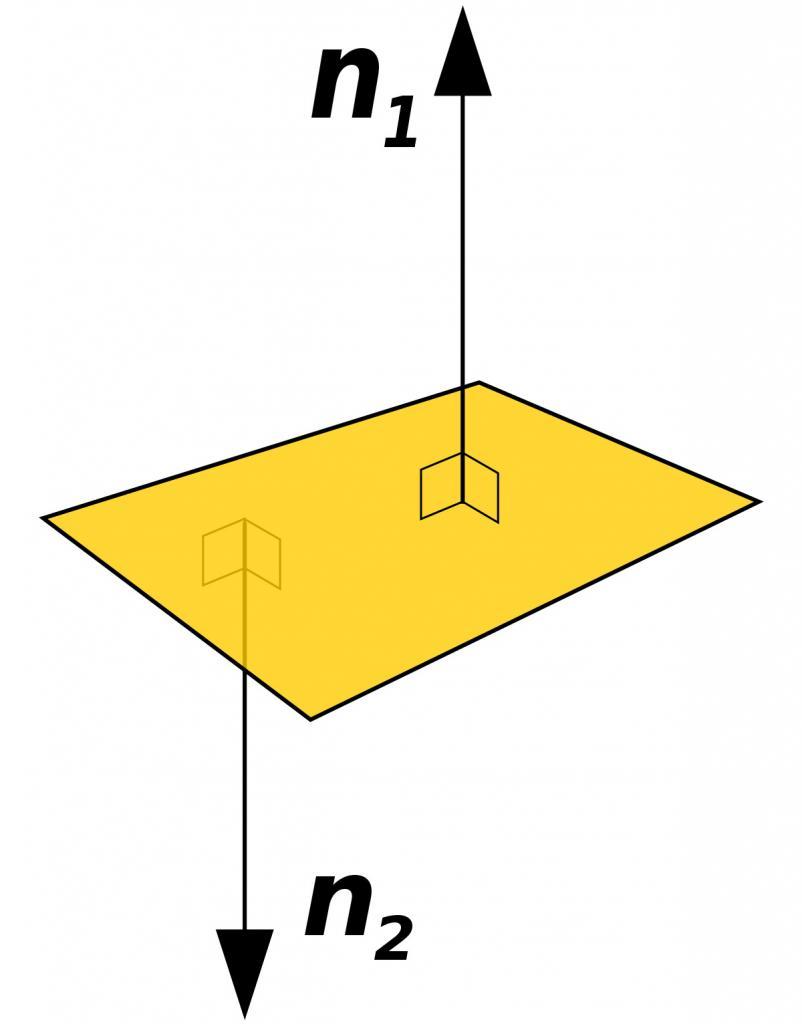
Прежде чем говорить об угле между двумя плоскостями, следует хорошо разобраться, о каком элементе в геометрии пойдет речь. Разберемся в терминологии. Плоскость представляет собой нескончаемую совокупность точек в пространстве, соединяя между собой которые, мы получим вектора. Последние будут по отношению к некоторому одному вектору перпендикулярны. Его принято называть нормалью к плоскости.

Вам будет интересно: Физика строения вещества. Открытия. Эксперименты. Расчеты

На рисунке выше показана плоскость и два нормальных вектора к ней. Видно, что лежат на одной прямой оба вектора. Угол между ними составляет 180o.

Уравнения

Между двумя плоскостями угол можно определить, если известно математическое уравнение рассматриваемого геометрического элемента. Существует несколько видов подобных уравнений, названия которых перечислены ниже:

Эти три вида являются наиболее удобными при решении различного рода задач, поэтому они чаще всего используются.

Уравнение общего типа выглядит следующим образом:

A*x + B*y + C*z + D = 0.

Здесь x, y, z — координаты произвольной точки, принадлежащей данной плоскости. Параметры A, B, C и D представляют собой числа. Удобство этой формы записи заключается в том, что числа A, B, C являются координатами нормального к плоскости вектора.

Векторная форма записи плоскости может быть представлена следующим образом:

x, y, z) = (x0, y0, z0) + α*(a1, b1, c1) + β*(a2, b2, c2).

Здесь (a2, b2, c2) и (a1, b1, c1) — параметры двух векторов координаты, которые принадлежат рассматриваемой плоскости. Точка (x0, y0, z0) также лежит в этой плоскости. Параметры α и β могут принимать независимые друг от друга и произвольные значения.

Наконец, уравнение плоскости в отрезках представляют в следующем математическом виде:

Здесь p, q, l — конкретные числа (в том числе отрицательные). Этот вид уравнения удобен, когда необходимо изобразить в прямоугольной системе координат плоскость, поскольку числа p, q, l показывают точки пересечения с осями x, y и z плоскости.

Заметим, что каждый вид уравнения может быть преобразован в любой другой с помощью несложных математических операций.

Формула угла между двумя плоскостями

Теперь рассмотрим следующий нюанс. В трехмерном пространстве две плоскости могут располагаться всего двумя способами. Либо пересекаться, либо быть параллельными. Между двумя плоскостями углом называется то, что расположено между их векторами направляющими (нормальными). Пересекаясь, 2 вектора образуют 2 угла (острый и тупой в общем случае). В качестве угла между плоскостями принято считать острый. Рассмотрим уравнение.

Формула угла между двумя плоскостями имеет вид:

Несложно догадаться, что это выражение является прямым следствием из скалярного произведения нормальных векторов n1¯ и n2¯ для рассматриваемых плоскостей. Модуль скалярного произведения в числителе указывает на то, что угол θ будет принимать только значения от 0o до 90o. Произведение модулей нормальных векторов в знаменателе означает произведение их длин.

Отметим, если (n1¯*n2¯) = 0, то плоскости пересекаются под прямым углом.

Пример задачи

Разобравшись, что называется углом между двумя плоскостями, решим следующую задачу. В качестве примера. Итак, необходимо вычислить угол между такими плоскостями:

(x, y, z) = (2, 0, -1) + α*(1, 1, -1) + β*(0, 2, 3).

Для решения задачи необходимо знать направляющие вектора плоскостей. Для первой плоскости нормальный вектор равен: n1¯ = (2, -3, 0). Чтобы найти второй плоскости нормальный вектор, следует умножить вектора, стоящие после параметров α и β. В результате получим вектор: n2¯ = (5, -3, 2).

Для определения угла θ воспользуемся формулой из предыдущего пункта. Получаем:

= arccos (19/√(13*38)) = 0,5455 рад.

Рассчитанный угол в радианах соответствует 31,26o. Таким образом, плоскости из условия задачи пересекаются под углом 31,26o.

Угол между плоскостями. Перпендикулярность плоскостей

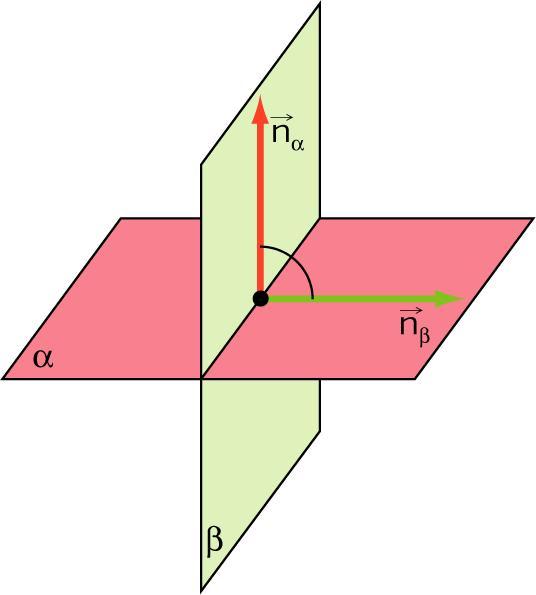
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.

Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны,

Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:

Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.