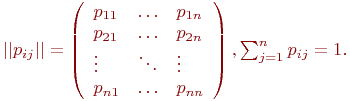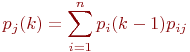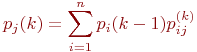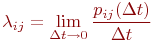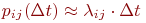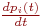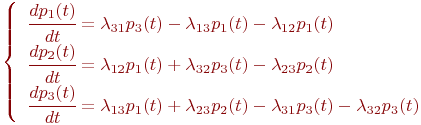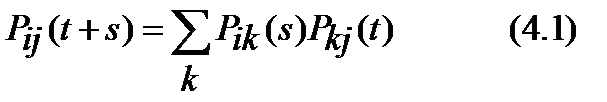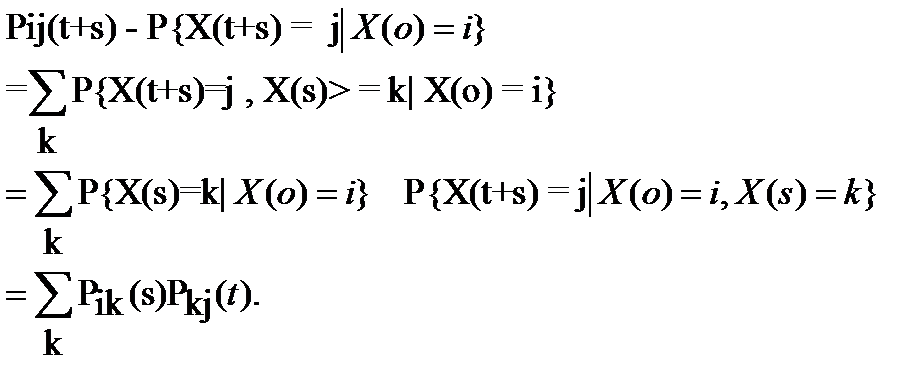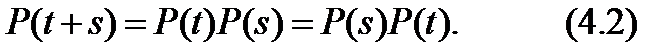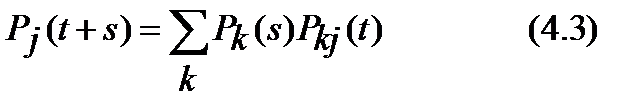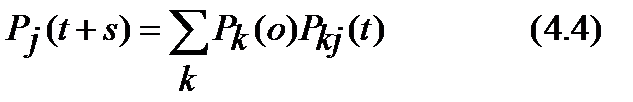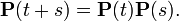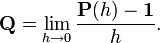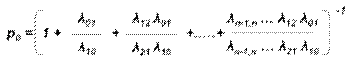Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 
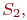
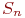
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 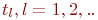
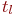
Известны вероятности перехода 

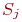
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 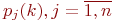

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
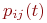
Значения 
Значения 
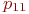
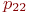
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 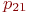
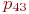
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 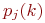
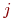

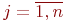
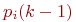
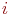

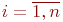
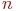

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 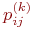

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 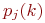
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 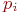

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 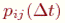


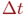
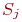
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

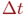
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 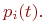
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 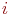
5. В правой части записывается алгебраическая сумма произведений 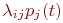
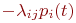
6. Определить начальные условия и решить систему дифференциальных уравнений.
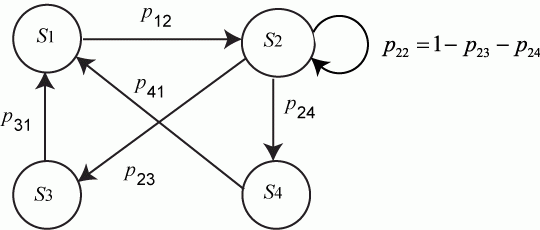
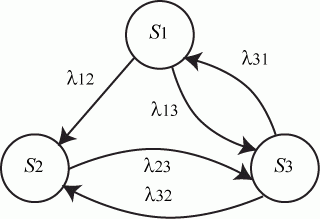
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 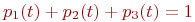
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 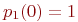
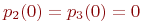
Дата добавления: 2015-04-03 ; просмотров: 7848 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнения Колмогорова — Чепмена
Дата добавления: 2014-04-25 ; просмотров: 6149 ; Нарушение авторских прав
Переходные вероятности Рij(t) удовлетворяют уравнению Колмогорова – Чепмена
Это уравнение отражает тот факт, что марковская система, переходя из состояния i в состояние j за время t+s, сначала за время s из состояния i переходит в некоторое промежуточное состояние k, a затем за время t из состояния k переходит в состояние j, причем вероятность второго перехода не зависит от того, каким образом было достигнуто состояние k.
Докажем уравнение Колмогорова — Чепмена. С помощью формулы полной вероятности пишем
Здесь четвертое равенство написано на основании марковского свойства и свойства однородности процесса X(t). В матричной форме уравнение Колмогорова — Чепмена записывается как
Для безусловных вероятностей состояний рj(t) = P
которое можно вывести из (4.1), если в (4.1) слева и справа умножить на рi (0) и затем просуммировать по всем индексам i = 0, ±1 , ±2 . Если в (4.3) s = 0, то
| | | следующая лекция ==> | |
| Марковское свойство | | | Дифференциальные уравнения Колмогорова |
Не нашли то, что искали? Google вам в помощь!
Уравнение Колмогорова — Чепмена
Уравнение Колмогорова — Чепмена для однопараметрического семейства непрерывных линейных операторов P(t) 
Чаще всего этот термин используется в теории однородных марковскихслучайных процессов, где P(t) 
Для неоднородных процессов рассматриваются двухпараметрические семейства операторов 

Для систем с дискретным временем параметры t,h,s принимаютнатуральные значения.
Прямое и обратное уравнения Колмогорова
Формально дифференцируя уравнение Колмогорова—Чепмена по sпри s = 0 получаем прямое уравнение Колмогорова:
Формально дифференцируя уравнение Колмогорова — Чепмена по tпри t = 0 получаем обратное уравнение Колмогорова
Необходимо подчеркнуть, что для бесконечномерных пространств оператор Q уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.
Примеры
Рассмотрим однородные марковские случайные процессы в R n для которых оператор переходных вероятностей P(t) задаётся переходной плотностью p(t,x,y): вероятность перехода из области U в область Wза время t есть 
При 


Тогда оператор 


а обратное уравнение Колмогорова
Пусть оператор 
(это означает, что q(x,y) есть линейная комбинация первых и вторых производных δ(x − y) с непрерывными коэффициентами). Матрицаaij симметрична. Пусть она положительно определена в каждой точке (диффузия). Прямое уравнение Колмогорова имеет вид
Это уравнение называется уравнением Фоккера — Планка. Вектор bjв физической литературе называется вектором сноса, а матрица aij —тензором диффузии Обратное уравнение Колмогорова в этом случае
Модели СМО, описываемые типа «гибель и размножение», их характеристики
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов – так называемый процесс гибели и размножения.
Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис.1:
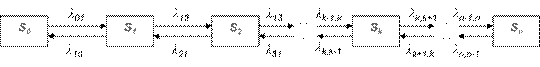
Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния Sk возможны переходы только в состояние Sk-1, либо в состояние Sk+1.* (При анализе численности популяций считают, что состояние Sk соответствует численности популяции равной k, и переход системы из состояния Sk в состояние Sk+1 происходит при рождении одного члена популяции, а переход в состояние Sk-1 – при гибели одного члена популяции. )
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями λk,k+1 или λk+1,k.
По графу, представленному на рис. 1, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений получим:
для состояния S0
для состояния S1 – (λ12 + λ10 ) p1 = λ01 p0 + λ21 p2, которое с учетом (1) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
Решая систему (3), (4), можно получить:
Подставляя p1, p2. pn в нормировочное условие, получим:
Легко заметить, что в формулах (5) для p1, p2,…, pn коэффициенты при p0 есть слагаемые, стоящие после единицы в формуле (6). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния Sk (k=1, 2, …, n), а знаменатели – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния Sk
http://life-prog.ru/1_29278_uravneniya-kolmogorova—chepmena.html
http://lektsii.org/17-9177.html