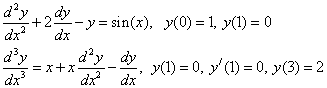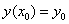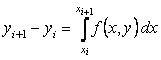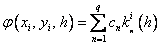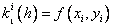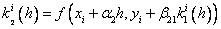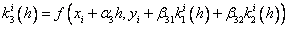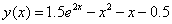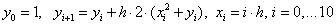По численным методам разностные уравнения

По численным методам разностные уравнения

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,у’)=0 или у’=f(x,y). Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Рассмотрим несколько численных методов решения дифференциальных уравнений первого порядка. Описание численных методов приводится для уравнения в виде у’=f(x,y).

Рассмотрим два варианта вывода расчетных формул

Численный метод нелинейного оценивания на основе разностных уравнений Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Зотеев Владимир Евгеньевич

Рассматривается новый численный метод оценки параметров нелинейных математических моделей , в основе которого лежат разностные уравнения, описывающие результаты наблюдений. Алгоритм численного метода содержит следующие шаги: построение линейно-параметрической дискретной модели исследуемого процесса в форме разностных уравнений, коэффициенты которых известным образом связаны с параметрами нелинейной математической модели ; формирование на основе разностных уравнений обобщенной регрессионной модели ; вычисление оценки начального приближения и уточнения среднеквадратичных оценок коэффициентов обобщенной регрессионной модели на основе итерационной процедуры; вычисление оценок параметров нелинейной математической модели на основе среднеквадратичных оценок коэффициентов разностных уравнений; оценка погрешности результатов вычислений на основе методов статистической обработки данных эксперимента. Предлагаются различные подходы к построению систем разностных уравнений для математических моделей в форме нелинейных функциональных зависимостей. Получены соотношения, лежащие в основе итерационного процесса уточнения коэффициентов обобщенной регрессионной модели , построенной на основе разностных уравнений. Описана процедура оценки погрешности результатов вычислений параметров нелинейных функциональных зависимостей, известным образом связанных с коэффициентами системы разностных уравнений . Применение численного метода на основе разностных уравнений проиллюстрировано на примерах оценки параметров математической модели линейного осциллятора с затуханием, модели свободных колебаний диссипативной механической системы с турбулентным трением, а также параметров логистического тренда, описываемого функцией Верхулста (Перла-Рида).

Похожие темы научных работ по математике , автор научной работы — Зотеев Владимир Евгеньевич

A numerical method of nonlinear estimation based on difference equations

The article considers a new numerical method for estimating the parameters of nonlinear mathematical models based on difference equations describing the results of observations. The algorithm of the numerical method includes: the construction of a linear-parametric discrete model of the process under study in the form of difference equations, the coefficients of which are known to be associated with the parameters of a nonlinear mathematical model ; the formation of a generalized regression model based on the difference equations; the calculation of the initial approximation estimate and the iterative procedure for refining the mean-square estimates of the coefficients of the generalized regression model ; the calculation of the estimates of the parameters of the nonlinear mathematical model based on the mean-square estimates of the coefficients of the difference equations; evaluation of the error of the results of calculations based on the methods of statistical processing of experimental data. Various approaches to the construction of systems of difference equations for mathematical models in the form of nonlinear functional dependencies are proposed. The relations underlying the iterative process of refining the coefficients of the generalized regression model constructed on the basis of difference equations are obtained. The procedure for estimating the error of the results of calculations of the parameters of nonlinear functional dependencies, which are known to be associated with the coefficients of the system of difference equations , is described. The application of the numerical method based on the difference equations is illustrated by the examples of estimation of the parameters of the mathematical model of the linear oscillator with attenuation, the model of free oscillations of the dissipative mechanical system with turbulent friction, as well as the parameters of the logistic trend described by the Verhulst (Pearl-Reed) function.

Текст научной работы на тему «Численный метод нелинейного оценивания на основе разностных уравнений»

Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2018. Т. 22, № 4. С. 669-701 ISSN: 2310-7081 (online), 1991-8615 (print) d http://doi.org/10.14498/vsgtu1643

Математическое моделирование, численные методы и комплексы программ

Численный метод нелинейного оценивания на основе разностных уравнений

Самарский государственный технический университет, Россия, 443100, Самара, ул. Молодогвардейская, 244.

Рассматривается новый численный метод оценки параметров нелинейных математических моделей, в основе которого лежат разностные уравнения, описывающие результаты наблюдений. Алгоритм численного метода содержит следующие шаги:

— построение линейно-параметрической дискретной модели исследуемого процесса в форме разностных уравнений, коэффициенты которых известным образом связаны с параметрами нелинейной математической модели;

— формирование на основе разностных уравнений обобщенной регрессионной модели;

— вычисление оценки начального приближения и уточнения среднеквадратичных оценок коэффициентов обобщенной регрессионной модели на основе итерационной процедуры;

— вычисление оценок параметров нелинейной математической модели на основе среднеквадратичных оценок коэффициентов разностных уравнений;

— оценка погрешности результатов вычислений на основе методов статистической обработки данных эксперимента.

Предлагаются различные подходы к построению систем разностных уравнений для математических моделей в форме нелинейных функциональных зависимостей. Получены соотношения, лежащие в основе итерационного процесса уточнения коэффициентов обобщенной регрессионной модели, построенной на основе разностных уравнений. Описана процедура оценки погрешности результатов вычислений параметров нелинейных функциональных зависимостей, известным образом связанных с коэффициентами системы разностных уравнений. Применение

3 ©® Контент публикуется на условиях лицензии Creative Commons Attribution 4.0 International (https://creativecommons.org/licenses/by/4.0/deed.ru) Образец для цитирования

Зотеев В. Е. Численный метод нелинейного оценивания на основе разностных уравнений // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки, 2018. Т. 22, № 4. С. 669-701. doi: 10.14498/vsgtu1643. Сведения об авторе

Владимир Евгеньевич Зотеев А http://orcid.org/0000-0001-7114-4894 доктор технических наук, доцент; профессор каф. прикладной математики и информатики; e-mail: zoteev-ve@mail.ru

численного метода на основе разностных уравнений проиллюстрировано на примерах оценки параметров математической модели линейного осциллятора с затуханием, модели свободных колебаний диссипативной механической системы с турбулентным трением, а также параметров логистического тренда, описываемого функцией Верхулста (Перла-Рида).

Ключевые слова: математическая модель, нелинейный регрессионный анализ, система разностных уравнений, обобщенная регрессионная модель, среднеквадратическое оценивание, статистическая обработка результатов эксперимента.

Получение: 14 сентября 2018 г. / Исправление: 5 ноября 2018 г. / Принятие: 12 ноября 2018 г. / Публикация онлайн: 18 декабря 2018 г.

Введение. Одной из основных проблем при построении математических моделей по результатам наблюдений, полученных в ходе эксперимента или натурных испытаний, является нелинейность математической модели относительно ее параметров. В тех случаях, когда форма математической модели однозначно не обусловлена априорной информацией, полученной на основе физических, химических или иных законов, описанных, например, в виде уравнений математической физики, широко используются линейные регрессионные модели, оценивание и статистический анализ параметров которых, как правило, не вызывает каких-либо затруднений [1—3].

Однако достаточно часто математические модели в форме функциональных зависимостей, описывающих исследуемый процесс или взаимосвязь между характеристиками объекта исследования, строятся на основе решения систем интегро-дифференциальных уравнений, нелинейных по своей природе. Причем нередко линеаризация полученных соотношений настолько упрощает математическую модель, что применение ее в задаче параметрической идентификации становится не только нецелесообразным, но и практически бессмысленным. Таким образом, проблема нелинейного оценивания — вычисления параметров нелинейных математических моделей по результатам наблюдений — всегда была и остается важнейшей проблемой при математическом моделировании.

Пусть математическая модель наблюдаемого процесса описывается нелинейной функциональной зависимостью вида у = f (1,а\,а2. ,ап), где аг, а2, . ап — параметры модели; п — число параметров; £ е [0, те) — аргумент функциональной зависимости, в частности, имеющий размерность времени. При равномерной дискретизации с периодом т: = тк, к = 0,1, 2. отсюда получаем дискретную математическую модель вида у = f (тк, аг,а2. ап), к = 0,1, 2, 3 . нелинейную по параметрам аг, а2. ап.

Пусть у к — результаты наблюдений (например, данные эксперимента), к = 0,1,2,3. Ы — 1; N — объем выборки результатов наблюдений. Тогда математическую модель, описывающую результаты наблюдений, можно представить в виде

Ук = / (тк, а\,а2. ап) + ек, к = 0,1,2,3. Ж — 1, (1)

где — разброс результатов наблюдений относительно модели ук при заданных значениях ее параметров (остатки). В векторной форме модель (1) имеет

где у е , у = / (а) е Мга, ее , а = (аъа2. ап)т е Мга.

Уравнение (1) описывает регрессионную модель, нелинейную по своим параметрам а\, а2. ап. В качестве критерия близости модели (1) результатам наблюдений у^ в регрессионном анализе принимается норма разности в евклидовом пространстве N-мерных векторов [2,3]:

где у, у G Е^ со скалярным произведением

\\у — У\\ = (У — У^ — У) = (У — у)Т(у — у).

С учетом выбранного критерия близости параметры нелинейной регрессионной модели (1) находятся из минимизации нелинейной функции

Q(ai,a2, . ап) = \\е\\2 = \\у — у\\2 = ^ [ук — f(r к, äi, а2. än)] ^ min.

В такой постановке эта задача относится к задаче нелинейного оценивания и может быть решена методами нелинейной регрессии, описанными в 3.

1. Классические методы нелинейного оценивания [2—9]. Известные традиционно применяемые в практике построения математических моделей методы нелинейного оценивания можно разбить на три основные группы. К первой группе относятся численные методы поиска минимума функции нескольких переменных, среди которых наибольшее применение нашли градиентный метод, метод наискорейшего спуска и метод сопряженных градиентов [3,10]. В основе этих методов лежит вычисление градиента функции Q(ä):

gradQ(ä) = -öQ = —2WT[y — f(ä)],

где Wт — матрица Якоби размера [Nxn], элементы которой = —

значения производных функции f(ä) по параметрам äj, j = 1, n, вычисленные в точках tк, к = 0,1, 2. N — 1.

Метод скорейшего спуска отличается от градиентного метода оптимальным выбором шага на каждой итерации. В свою очередь метод сопряженных направлений отличается от метода наискорейшего спуска только выбором направления уменьшения функции на каждом шаге — вектор

■p(i) = gradQ(a(i)) + a(i)p(i-1)

вместо вектора градиента gradQ(a(t)). Алгоритм метода сопряженных направлений может быть описан следующей системой соотношений:

а(°) =0, р(°) = цгаё((а(°)), а« = 1 2,

р(г) = ёга 0. Метод Левенберга—Марквардта целесообразно использовать при плохо обусловленной матрице Р(а) = 2Ш(а)тЖ(а). Этот метод имеет много общего с методом регуляризации (ridge-оценок), применяемом при решении плохо обусловленных систем линейных алгебраических уравнений. Алгоритм метода строится на основе метода Ньютона—Гаусса и описывается рекуррентной формулой

а (*+1) = а« + [Ж (а« )тЖ (а«) + р« Да«)] (а«)т [у — Да«)],

где ^ > 0 — малый параметр, = Е в методе Левенберга (Е — еди-

ничная матрица) и = Е ■ (а^^Ш(а(г))] в методе Марквардта.

Стратегия выбора параметра ^ описана в [3].

К третьей группе классических методов нелинейного оценивания можно отнести методы, в основе которых лежит линеаризация нелинейной математической модели [3]. Различают параметрическую линеаризацию нелинейной функциональной зависимости посредством разложения в ряд Тейлора и линеаризацию посредством некоторого подходящего преобразования нелинейной функции регрессоров (например, с помощью логарифмирования). В первом случае задача сводится к линейной регрессии, причем алгоритм вычислений описывается той же итерационной формулой, что и в методе Ньютона—Гаусса.

Завершая анализ известных методов нелинейного оценивания, можно сделать следующие выводы.

Во-первых, эти методы, как правило, требуют вычисления производных сложной нелинейной функции до второго порядка включительно.

Во-вторых, в методе Ньютона—Гаусса, а также при параметрической линеаризации на основе разложения в ряд Тейлора используется аппроксимация нелинейной регрессионной модели линейной, что приводит к методической погрешности в результатах вычислений и, как следствие, смещению оценок параметров модели.

В-третьих, основной проблемой при применении известных методов является проблема выбора начального приближения, обеспечивающего сходимость итерационной процедуры к точке минимума. Этот основной недостаток существенно ограничивает область применения методов нелинейной регрессии при построении математических моделей по результатам эксперимента.

Предлагаемый новый численный метод нелинейного оценивания в формате описанной выше систематизации может быть отнесен к третьей группе методов, так как в нем оценивание параметров нелинейной регрессии сводится к вычислению коэффициентов линейно параметрической дискретной модели (ЛПДМ) в форме разностных уравнений. Однако в отличие от параметрической линеаризации на основе разложения в ряд Тейлора, ЛПДМ в форме разностных уравнений эквивалентна дискретной нелинейной модели, и методическая погрешность, обусловливающая смещение оценок параметров модели, отсутствует. Вторым существенным достоинством предлагаемого метода является нахождение оценки начального приближения вектора коэффициентов ЛПДМ непосредственно в процессе реализации алгоритма вычислений; при этом находить оценку начального приближения вектора параметров нелинейной модели не нужно.

2. Алгоритм численного метода нелинейного оценивания на основе разностных уравнений. В основе численного метода нелинейного оценивания на основе разностных уравнений лежит переход от нелинейной по параметрам математической модели к линейно параметрической дискретной модели, коэффициенты которой известным образом связаны с искомыми параметрами. Построенная на основе ЛПДМ обобщенная регрессионная модель, описывающая результаты наблюдений, позволяет свести задачу нелинейного регрессии к вычислению среднеквадратичных оценок коэффициентов ЛПДМ, т.е. к задаче линейного прикладного регрессионного анализа, решение которой не вызывает особых затруднений.

Численный метод нелинейного оценивания на основе разностных уравнений включает следующие основные этапы [8]:

— построение математической модели исследуемого процесса в форме линейных разностных уравнений, коэффициенты которых известным образом связаны с параметрами нелинейной математической модели;

— формирование разностных уравнений, описывающих результаты наблюдений;

— формирование на основе разностных уравнений элементов обобщенной регрессионной модели;

— вычисление оценки начального приближения коэффициентов обобщенной регрессионной модели;

— итерационная процедура уточнения среднеквадратичных оценок коэффициентов обобщенной регрессионной модели;

— вычисление оценок параметров нелинейной математической модели на основе среднеквадратичных оценок коэффициентов разностных уравнений;

— оценка погрешности результатов вычислений на основе методов статистической обработки данных эксперимента.

Рассмотрим поэтапную реализацию описанного выше алгоритма численного метода на основе разностных уравнений.

3. Построение математической модели исследуемого процесса в форме разностных уравнений. Под математической моделью исследуемого процесса в форме разностных уравнений будем понимать линейную комбинацию функций (

Ьк+1 (Ук, Ук-Ъ . Ук-Г) = (Ук, Ук-Ъ . Ук-Г), (2)

где к = 0,1, 2. Ы — 1. При к Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

С учетом известных формул ^-преобразования [9]:

По численным методам разностные уравнения

Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений

5. Численное решение обыкновенных дифференциальных уравнений

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:

, где x – независимая переменная, — i-ая производная от искомой функции. n — порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных , т.е. общее решение имеет вид .

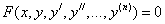
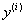
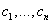
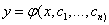
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

Примеры краевых задач:

Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.

Численные методы решения задачи Коши для ОДУ первого порядка

Постановка задачи. Найти решение ОДУ первого порядка

на отрезке при условии

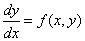
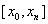
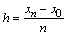
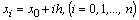
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точки промежутка [x₀, x_n].

Целью является построение таблицы

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке 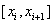, получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

,

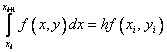
то получим явную формулу Эйлера:

, .

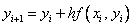
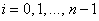
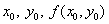
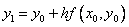
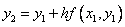
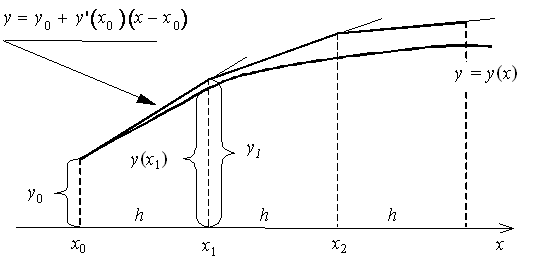
Зная , находим , затем т.д.

Геометрическая интерпретация метода Эйлера:

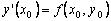
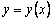
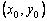
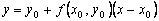
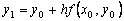
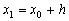
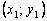
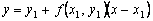
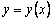
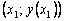
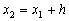
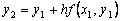
Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной , можно записать уравнение касательной к графику искомой функции в точке : . При достаточно малом шаге h ордината этой касательной, полученная подстановкой в правую часть значения , должна мало отличаться от ординаты y(x₁) решения y(x) задачи Коши. Следовательно, точка пересечения касательной с прямой x = x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую , которая приближенно отражает поведение касательной к в точке . Подставляя сюда (т.е. пересечение с прямой x = x₂), получим приближенное значение y(x) в точке x₂: и т.д. В итоге для i–й точки получим формулу Эйлера.

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

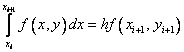
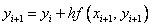
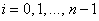
Если использовать формулу правых прямоугольников: , то придем к методу

, .

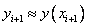
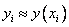
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Модифицированный метод Эйлера: в данном методе вычисление 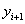состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(x_i+1) по формуле вида

,

.

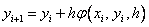
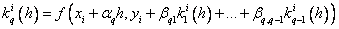
Здесь a_n, b_nj, p_n, 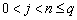– некоторые фиксированные числа (параметры).

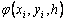
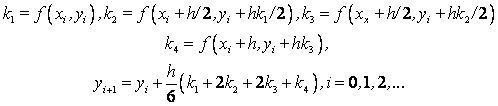
При построения методов Рунге–Кутты параметры функции (a_n, b_nj, p_n) подбирают таким образом, чтобы получить нужный порядок аппроксимации.

Схема Рунге – Кутта четвертого порядка точности:

Пример. Решить задачу Коши:

.

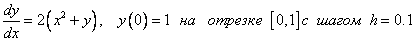
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.

Точное решение:

Расчетные формулы по явному методу Эйлера для данного примера:

Расчетные формулы модифицированного метода Эйлера: