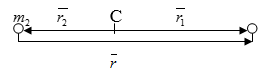По уравнениям движения двух тел

По уравнениям движения двух тел х1 = 20t и х2 = 250 — 5t определите: а) место и время встречи этих тел;

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,292
• гуманитарные 33,622
• юридические 17,900
• школьный раздел 607,160
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

По уравнениям движения двух тел

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Типовая задача «Уравнение координаты (нахождение неизвестной величины)»

Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»

Задача № 2. Движение двух тел задано уравнениями x₁ = 20 – 8t и х₂ = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»

Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.

Типовая задача «График координаты. Движение нескольких тел»

Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.

ЗАДАЧИ ПОСЛОЖНЕЕ

Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ:

Задача № 6. По графикам на рисунке напишите уравнения движения x = x(t) . Из уравнений и графиков найдите координаты тел через 5 с , скорости движения тел, время и место встречи второго и третьего тел.

РЕШЕНИЕ:

Задача № 7. ОГЭ Расстояние ( S ) между городами М и К = 250 км . Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч , из города К — со скоростью ν₂ = 40 км/ч . Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.

Задача № 8. ЕГЭ Скорость течения реки v_p = 1 м/с , скорость лодки относительно воды v₀ = 2 м/с . Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м ?

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.

Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.

Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.

При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.

В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:

Задача двух тел

Вы будете перенаправлены на Автор24

Приведенная масса

Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.

В связи с этим важна задача о замкнутой системе двух точек, называемая задачей двух тел. Она имеет простое и исчерпывающее решение — сводится к основной задаче динамики одной материальной точки. Решение задачи двух тел используется в небесной механике, описывающей движение планет и их спутников в Солнечной системе, в задачах на столкновение частиц, в статистической физике и других вопросах.

Рассмотрим замкнутую систему двух материальных точек, взаимодействующих между собой. Как известно центр масс такой системы движется равномерно и прямолинейно (или покоится). Задача просто решается в системе с началом в центре масс, движущейся поступательно (такая система называется Ц-системой).

Обозначим массы частиц через $m_ <1>$ и $m_ <2>$ и их радиус-векторы, проведенные от центра масс, соответственно $\overline >$ и $\overline >$. Пусть $\overline$- вектор, проведенный от точки $m_ <2>$ к $m_ <1>$. Из определения радиус-вектора центра масс имеем:

Непосредственно из рисунка следует соотношение между радиус-векторами:

$\overline_ <1>=\overline_ <2>+\overline$. (1)

Два последних равенства позволяют выразить радиус-векторы $\overline >$ и $\overline >$ через вектор $\overline$, соединяющий точки $m_ <2>$ и $m_ <1>$. Имеем:

Запишем основные уравнения для движения обеих точек в Ц-системе:

Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.

Готовые работы на аналогичную тему

Пользуясь выражениями для радиус-векторов (2), исключим из основных уравнений (3) $\overline >$ и $\overline >$. Тогда получаем уравнения движения:

Так как по третьему закону Ньютона $\overline_ <2,1>(r)=-\overline_ <1,2>(r)$, оба уравнения становятся тождественными, и движение системы двух точек, в результате их взаимодействия эквивалентно движению одной точки в соответствии с уравнением:

Уравнение (4) отличается от известного уравнения движения материальной точки в поле заданной силы только тем, что вместо массы $m$здесь выступает комбинация масс двух точек:

Величина $m’$ называется приведенной массой.

Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:

Но при использовании результатов решения уравнения (6) необходимо помнить, что точка $m’$, движущаяся на конце радиус-вектора $\overline$под действием силового центра в начале координат Ц-системы, является не реальной, а изображающей движение системы. От ее движения, после того как уравнение (6) проинтегрировано, следует переходить к реальному движению двух материальных точек $m_ <2>$ и $m_ <1>$.

Движение двух материальных точек в системе центра масс

Движение изображающей точки в соответствии с уравнением (6) будет плоским. Пусть кинематическое уравнение движения найдено: $\overline=\overline(t)$.

В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:

Очевидно, что траектория движения изображающей точки и точек $m_ <2>$ и $m_ <1>$ будут подобными кривыми относительно центра масс, а отношение подобия есть обратное отношение масс, т.е.:

Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:

Задача двух тел решена.

Момент импульса для системы двух точек имеет вид: $\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|$. Необходимо записать выражение для собственного момента импульса системы через приведенную массу.

Момент импульса системы двух точек: $\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|$.

Найти: собственный момент импульса системы — ?

Момент импульса системы двух точек:

\[\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|.\]

Внесем сюда выражения $\overline >$ и $\overline >$через вектор $\overline$, выражающийся формулой (7) и получим равенство:

\[\overline=\frac m_ <2>> +m_ <2>> \left|\overline\overline_ <1>\right|-\frac m_ <2>> +m_ <2>> \left|\overline\overline_ <2>\right|=\frac m_ <2>> +m_ <2>> (\overline\left|\overline_ <1>-\overline_ <2>\right|).\]

Вектор $\overline_ <1>-\overline_ <2>$ есть скорость $\overline$первой частицы относительно второй или скорость изображающей точки $\overline$ и окончательный результат выражается равенством:

Ответ: собственный момент импульса системы $\overline=m'[\overline\overline<\cdot v>]$

задача о движении двух тел сводится к задаче о движении одной точки под действием заданной силы;

особую роль при этом играет приведенная масса системы, через нее выражаются основные динамические параметры системы — энергия, импульс, момент импульса.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 04 2021