По векторная форма уравнения плоскости

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

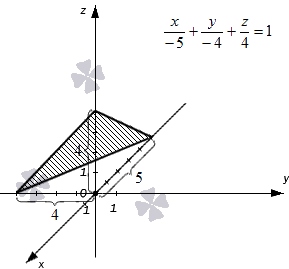
Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Уравнения прямых и плоскостей

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,\label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть \(A^<2>+B^<2>+C^ <2>\neq 0\). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,\label
$$
при условии \(A^<2>+B^ <2>\neq 0\).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения \eqref и \eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,\nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol-\boldsymbol_ <0>= t\boldsymbol.\label
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref в качестве \(t\), вектор \(\boldsymbol\) в этой формуле определит некоторую точку на прямой.

Уравнение \eqref называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol

\) и \(\boldsymbol\) ее направляющие векторы, а через \(\boldsymbol_<0>\) — радиус-вектор ее начальной точки \(M_<0>\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol\) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор \(\overrightarrowM> = \boldsymbol-\boldsymbol_<0>\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol

\) и \(\boldsymbol\) не коллинеарны, в этом и только этом случае \(\boldsymbol-\boldsymbol_<0>\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_<1>\) и \(t_<2>\), что
$$
\boldsymbol-\boldsymbol_ <0>= t_<1>\boldsymbol

+t_<2>\boldsymbol.\label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_<1>\) и \(t_<2>\). Наоборот, какие бы числа мы ни подставили как значения \(t_<1>\) и \(t_<2>\), уравнение \eqref определит некоторую точку плоскости.

Пусть \((x, y, z)\) и \((x_<0>, y_<0>, z_<0>)\) — координаты точек \(M\) и \(M_<0>\) соответственно, а векторы \(\boldsymbol

\) и \(\boldsymbol\) имеют компоненты \((p_<1>, p_<2>, p_<3>)\) и \((q_<1>, q_<2>, q_<3>)\). Тогда, раскладывая по базису обе части уравнения \eqref, мы получим параметрические уравнения плоскости
$$
x-x_ <0>= t_<1>p_<1>+t_<2>q_<1>,\ y-y_ <0>= t_<1>p_<2>+t_<2>q_<2>,\ z-z_ <0>= t_<1>p_<3>+t_<2>q_<3>.\label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой \(M_<0>(x_<0>, y_<0>)\) и направляющим вектором \(\boldsymbol(a_<1>, a_<2>)\) может быть записано в виде \eqref.

Уравнение \eqref линейное. Действительно, после преобразования оно принимает вид \(a_<2>x-a_<1>y+(a_<1>y_<0>-a_<2>x_<0>) = 0\), то есть \(Ax+By+C = 0\), где \(A = a_<2>\), \(B = -a_<1>\) и \(C = a_<1>y_<0>-a_<2>x_<0>\).

Вектор с координатами \((-B, A)\) можно принять за направляющий вектор прямой с уравнением \eqref в общей декартовой системе координат, а точку \eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор \(\boldsymbol(A, B)\) перпендикулярен прямой с уравнением \eqref.

Действительно, в этом случае \((\boldsymbol, \boldsymbol) = -BA+AB = 0\).

Пусть в уравнении прямой \(Ax+By+C = 0\) коэффициент \(B\) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,\label
$$
где \(k = -A/B\), а \(b = -C/B\). Мы видим, что к равно отношению компонент направляющего вектора: \(k = a_<2>/a_<1>\) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора \(a_<2>/a_<1>\) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от \(\boldsymbol_<1>\) к \(\boldsymbol_<2>\) (рис. 6.4).

Рис. 6.4. \(k=\operatorname\varphi = -1\). Прямая \(y=-x+1/2\)

Положив \(x = 0\) в уравнении \eqref, получаем \(y = b\). Это означает, что свободный член уравнения \(b\) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой \(B = 0\) и ее уравнение нельзя представить в виде \eqref, то обязательно \(A \neq 0\). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид \(x = x_<0>\), где \(x_ <0>= -C/A\) — абсцисса точки пересечения прямой с осью абсцисс.

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка \(M\) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки \(M_<0>\) компланарна направляющим векторам \(\boldsymbol

\) и \(\boldsymbol\). Эту компланарность можно выразить и равенством
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol

, \boldsymbol) = 0.\label
$$
Вектор \(\boldsymbol = [\boldsymbol

, \boldsymbol]\) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение \eqref в виде
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0.\label
$$

Уравнения \eqref и \eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в \eqref \(D = -(\boldsymbol_<0>, \boldsymbol)\), получим
$$
(\boldsymbol, \boldsymbol)+D = 0.\label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные \eqref и \eqref,
$$
(\boldsymbol-\boldsymbol_<0>, \boldsymbol) = 0\ \mbox<или>\ (\boldsymbol, \boldsymbol)+C = 0.\nonumber
$$
Первое из них выражает тот факт, что вектор \(\boldsymbol-\boldsymbol_<0>\) перпендикулярен ненулевому вектору \(\boldsymbol\), перпендикулярному направляющему вектору \(\boldsymbol\), и потому коллинеарен \(\boldsymbol\).

Пусть \(x, y, z\) — компоненты вектора \(\boldsymbol\) в общей декартовой системе координат. Тогда скалярное произведение \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\) при \(\boldsymbol \neq 0\) записывается линейным многочленом \(Ax+By+Cz+D\), где \((A^<2>+B^<2>+C^ <2>\neq 0)\).

Обратно, для любого линейного многочлена найдутся такие векторы \(\boldsymbol_<0>\) и \(\boldsymbol \neq 0\), что в заданной общей декартовой системе координат \(Ax+By+Cz+D = (\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Первая часть предложения очевидна: подставим разложение вектора \(\boldsymbol\) по базису в данное скалярное произведение:
$$
(x\boldsymbol_<1>+y\boldsymbol_<2>+z\boldsymbol_<3>-\boldsymbol_<0>, \boldsymbol),\nonumber
$$
раскроем скобки и получим многочлен \(Ax+By+Cz+D\), в котором \(D = -(\boldsymbol_<0>, \boldsymbol)\) и
$$
A = (\boldsymbol_<1>, \boldsymbol),\ B = (\boldsymbol_<2>, \boldsymbol),\ C = (\boldsymbol_<3>, \boldsymbol)\label
$$
\(A\), \(B\) и \(C\) одновременно не равны нулю, так как ненулевой вектор \(\boldsymbol\) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор \(\boldsymbol\) из равенств \eqref, считая \(A\), \(B\) и \(C\) заданными. Из ранее доказанного утверждения 10 следует, что
$$
\boldsymbol = \frac_<2>, \boldsymbol_<3>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<3>, \boldsymbol_<1>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>+\frac_<1>, \boldsymbol_<2>]><(\boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>)>.\label
$$

Вектор \(\boldsymbol_<0>\) должен удовлетворять условию \(D = -(\boldsymbol_<0>, \boldsymbol)\). Один из таких векторов можно найти в виде \(\boldsymbol_ <0>= \lambda \boldsymbol\). Подставляя, видим, что \(-\lambda(\boldsymbol, \boldsymbol) = D\), откуда \(\boldsymbol_ <0>= -D\boldsymbol/|\boldsymbol|^<2>\).

Итак, мы нашли векторы \(\boldsymbol\) и \(\boldsymbol_<0>\) такие, что линейный многочлен записывается в виде
$$
x(\boldsymbol_<1>, \boldsymbol)+y(\boldsymbol_<2>, \boldsymbol)+z(\boldsymbol_<3>, \boldsymbol)-(\boldsymbol_<0>, \boldsymbol),\nonumber
$$
который совпадает с требуемым \((\boldsymbol-\boldsymbol_<0>, \boldsymbol)\).

Если система координат декартова прямоугольная, то вектор с компонентами \(A\), \(B\), \(C\) является нормальным вектором для плоскости с уравнением \(Ax+By+Cz+D = 0\).

Это сразу вытекает из формул \eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению \eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, \(\alpha_<1>, \alpha_<2>\), должны быть пропорциональны компонентам — \(B\), \(A\) направляющего вектора прямой.

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B.\label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения \eqref выполнено (с тем же \(\lambda\)) равенство
$$
C_ <1>= \lambda C.\label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами \((-B, A)\) и \((-B_<1>, A_<1>)\) — направляющие векторы прямых.

Докажем вторую часть. В равенствах \eqref и \eqref \(\lambda \neq 0\), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид \(Ax+By+C = 0\) и \(\lambda(Ax+By)+C_ <1>= 0\) при некотором \(\lambda\). Если, кроме того, существует общая точка \(M_<0>(x_<0>, y_<0>)\) обеих прямых, то \(Ax_<0>+By_<0>+C = 0\) и \(\lambda(Ax_<0>+By_<0>)+C_ <1>= 0\). Вычитая одно равенство из другого, получаем \(C_ <1>= \lambda C\), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0,\ A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0\nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число \(\lambda\), что
$$
A_ <1>= \lambda A,\ B_ <1>= \lambda B,\ C_ <1>= \lambda C.\label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений \eqref выполнено (с тем же \(\lambda\)) равенство
$$
D_ <1>= \lambda D.\label
$$

Если плоскости параллельны, то их нормальные векторы \(\boldsymbol\) и \(\boldsymbol_<1>\) коллинеарны, и существует такое число \(\lambda\), что \(\boldsymbol_ <1>= \lambda\boldsymbol\). В силу уравнений \eqref \(A_ <1>= (\boldsymbol_<1>, \boldsymbol_<1>) = \lambda(\boldsymbol_<1>, \boldsymbol) = \lambda A\). Аналогично доказываются и остальные равенства \eqref. Обратно, если равенства \eqref выполнены, то из формулы \eqref следует, что \(\boldsymbol_ <1>= \lambda\boldsymbol\). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия \eqref выражают не что иное, как коллинеарность векторов с компонентами \((A, B)\) и \((A_<1>, B_<1>)\). Точно так же условия \eqref означают коллинеарность векторов с компонентами \((A, B, C)\) и \((A_<1>, B_<1>, C_<1>)\). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
\begin
A& B\\
A_<1>& B_<1>
\end
= 0,\label
$$
а условие параллельности плоскостей — в виде
$$
\begin
B& C\\
B_<1>& C_<1>
\end =
\begin
C& A\\
C_<1>& A_<1>
\end =
\begin
A& B\\
A_<1>& B_<1>
\end
= 0.\label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии \eqref система линейных уравнений
$$
Ax+By+C = 0,\ A_<1>x+B_<1>y+C_ <1>= 0,\nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от \(C\) и \(C_<1>\). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
\begin
A& B\\
A_<1>& B_<1>
\end
\neq 0.\nonumber
$$
то при любых \(C\) и \(C_<1>\) система имеет единственное решение \((x, y)\).

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
\left\<\begin
Ax+By+Cz+D = 0,\\
A_<1>x+B_<1>y+C_<1>z+D_ <1>= 0.
\end\right.\label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно \eqref означает, что хоть один из детерминантов отличен от нуля:
$$
\begin
B& C\\
B_<1>& C_<1>
\end^ <2>+
\begin
C& A\\
C_<1>& A_<1>
\end^ <2>+
\begin
A& B\\
A_<1>& B_<1>
\end^<2>
\neq 0.\label
$$

Разумеется, систему \eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой \eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = \frac><\alpha_<1>>,\ t = \frac><\alpha_<2>>,\ t = \frac><\alpha_<3>>,\nonumber
$$
и мы получаем два равенства
$$
\frac><\alpha_<2>> = \frac><\alpha_<3>>,\ \frac><\alpha_<1>> = \frac><\alpha_<3>>,\label
$$
или, в более симметричном виде,
$$
\frac><\alpha_<1>> = \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Уравнения \eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная \(x\)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, \(\alpha_<1>\), то уравнения прямой принимают вид
$$
x = x_<0>,\ \frac><\alpha_<2>> = \frac><\alpha_<3>>,\label
$$
Эта прямая лежит в плоскости \(x = x_<0>\) и, следовательно, параллельна плоскости \(x = 0\). Аналогично пишутся уравнения прямой, если в нуль обращается не \(\alpha_<1>\), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, \(\alpha_<1>\) и \(\alpha_<2>\), то прямая имеет уравнения
$$
x = x_<0>,\ y = y_<0>.\label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений \eqref. По условию \eqref один из детерминантов отличен от нуля. Допустим для определенности, что \(AB_<1>-A_<1>B \neq 0\). В силу утверждения 9 при любом фиксированном \(z\) система уравнений будет иметь единственное решение \((x, y)\), в котором \(x\) и \(y\), разумеется, зависят от \(z\). Они — линейные многочлены от \(z\): \(x = \alpha_<1>z+\beta_<1>\), \(y = \alpha_<2>z+\beta_<2>\).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя \(z\) на \(t\), получаем параметрические уравнения прямой
$$
x = \alpha_<1>t+\beta_<1>,\ y = \alpha_<2>t+\beta_<2>,\ z = t.\nonumber
$$

Первые две координаты начальной точки прямой \(M_<0>(\beta_<1>, \beta_<2>, 0)\) можно получить, решая систему \eqref при значении \(z = 0\).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты \((\alpha_<1>, \alpha_<2>, 1)\). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами \((A, B, C)\) и \(A_<1>, B_<1>, C_<1>\) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой \eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
\begin
B& C\\
B_<1>& C_<1>
\end,\
\begin
C& A\\
C_<1>& A_<1>
\end,\
\begin
A& B\\
A_<1>& B_<1>
\end.\label
$$

Вектор с компонентами \eqref есть направляющий вектор прямой с уравнениями \eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого \((\alpha_<1>, \alpha_<2>, \alpha_<3>)\) удовлетворяют уравнению \(A\alpha_<1>+B\alpha_<2>+C\alpha_ <3>= 0\), параллелен плоскости с уравнением \(Ax+By+Cz+D = 0\). Если, кроме того, он удовлетворяет уравнению \(A_<1>\alpha_<1>+B_<1>\alpha_<2>+C_<1>\alpha_ <3>= 0\), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами \eqref ненулевой в силу неравенства \eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

Векторное уравнение плоскости

Кроме того, плоскость может быть описана с помощью точки и вектора, перпендикулярного плоскости, называемой нормальным вектором.

Векторное уравнение плоскости имеет следующий вид:

Параметрическое уравнение → Векторное уравнение

Метод

1. Примите вектор положения из параметрического уравнения
2. Вычислите нормальный вектор
   • Вариант 1: используйте скалярное произведение
   • Вариант 2: используйте перекрестное произведение векторов
3. Вставьте вектор положения и нормальный вектор

Подсказка

Например

Вектор положения

Нормальный вектор

Вариант 1

Поскольку оба вектора направления перпендикулярны нормальному вектору $\vec=\begin x \\ y \\ z \end$, скалярное произведение должно привести к нулю.

Теперь можно вычислить скалярное произведение.

Выберите любое значение $z$ , например $z=4$

Вычислите $x$, используя I. (вставьте $y$)

Вариант 2

Теперь мы вычисляем только перекрестное произведение векторов.

Вставьте

$\text \left(\vec — \begin 2 \\ 1 \\ 1 \end\right) \cdot \begin 2 \\ -2 \\ 4 \end=0$

Векторное уравнение → параметрическое уравнение

Метод

1. Примите вектор положения, векторного уравнения
2. Используйте скалярное произведение для определения вектора направления
3. Вставьте вектор положения и вектор направления

Подсказка

Например

$\text \left(\vec — \begin 2 \\ 1 \\ 1 \end\right) \cdot \begin 2 \\ -2 \\ 4 \end=0$

Вектор положения

Вектор направления

Используя нормальный вектор, мы можем определить оба вектора направления, необходимые для Параметрического уравнения.

1. Вектор направления

Должен быть найден вектор, с которым скалярное произведение равно нулю.

Особенно легко заменить первую координату на 0,а затем поменять местами две другие координаты и изменить знак.

2 Вектор направления

Здесь последняя координата должна быть заменена на 0, а две другие координаты должны изменить знак.

Вставьте

$\text \vec = \begin 2 \\ 1 \\ 1 \end + r \cdot \begin 0 \\ -4 \\ -2 \end$ $+ s \cdot \begin -2 \\ -2 \\ 0 \end$