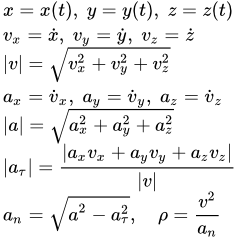Теоретическая механика: Решебник Яблонского:
Кинематика точки (К1)
Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по теме кинематика точки.
Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки M установить вид ее траектории и для момента времени t=t1 (c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 20.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 20) добавляется третье уравнение (табл. 22).
Координатный способ задания движения точки
Введение
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы применим основные результаты этой теории к координатному способу задания движения материальной точки.
Пусть мы имеем неподвижную прямоугольную систему координат с центром в неподвижной точке . При этом положение точки M однозначно определяются ее координатами (x, y, z). Координатный способ задания движения точки – это такой способ, при котором заданы зависимости координат от времени. То есть заданы три функции от времени (при трехмерном движении):
Далее мы приводим формулы вычисления кинематических величин и пример решения задачи для координатного способа задания движения.
Определение кинематических величин
Зная зависимости координат от времени , мы автоматически определяем радиус-вектор материальной точки M по формуле:
,
где – единичные векторы (орты) в направлении осей x, y, z .
Дифференцируя по времени , находим проекции скорости и ускорения на оси координат:
;
;
Модули скорости и ускорения:
;
.
Единичный вектор в направлении касательной к траектории:
.
Его можно определить двумя способами – по направлению скорости, или в противоположную сторону. Поэтому здесь в знаменателе стоит не модуль скорости, а алгебраическая величина скорости, которая, по абсолютной величине, равна модулю скорости, но может принимать как положительные, так и отрицательные значения: . Она является проекцией скорости на направление единичного вектора .
Алгебраическая величина тангенциального (касательного) ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории:
.
Вектор тангенциального (касательного) ускорения:
.
Здесь также, как и для скорости, – это скалярная величина, которая может принимать как положительные так и отрицательные значения: .
Нормальное ускорение:
.
Вектор нормального ускорения:
; .
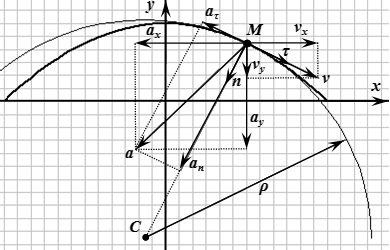
Единичный вектор в направлении главной нормали траектории (то есть единичный вектор, перпендикулярный касательной и направленный к центру кривизны траектории):
.
Здесь – это модуль нормального ускорения: . Нормальное ускорение всегда направлено к центру кривизны траектории. Оно не может быть направлено в противоположную сторону.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Пример решения задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения
По заданным уравнениям движения точки установить вид ее траектории и для момента времени найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
, см;
, см.
Решение
Определение вида траектории
Исключаем время из уравнений движения. Для этого перепишем их в виде:
; .
Применим формулу:
.
;
;
;
.
Итак, мы получили уравнение траектории:
.
Это уравнение параболы с вершиной в точке и осью симметрии .
Поскольку
, то
; или
.
Аналогичным образом получаем ограничение для координаты :
;
;
Таким образом, траекторией движения точки является дуга параболы
,
расположенная при
и .
Строим параболу по точкам.
| 0 | 6 |
| ± 3 | 5,625 |
| ± 6 | 4,5 |
| ± 9 | 2,625 |
| ± 12 | 0 |
Определяем положение точки в момент времени .
;
.
Определение скорости точки
Дифференцируя координаты и по времени , находим компоненты скорости.
.
Чтобы продифференцировать , удобно применить формулу тригонометрии:
. Тогда
;
.
Вычисляем значения компонент скорости в момент времени :
;
.
Модуль скорости:
.
Определение ускорения точки
Дифференцируя компоненты скорости и по времени , находим компоненты ускорения точки.
;
.
Вычисляем значения компонент ускорения в момент времени :
;
.
Модуль ускорения:
.
Алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление единичного вектора касательной к траектории. Выберем направление совпадающим с направлением скорости . Тогда ; алгебраическая величина тангенциального ускорения – это проекция полного ускорения на направление скорости :
.
Поскольку , то вектор тангенциального ускорения направлен противоположно скорости .
Нормальное ускорение:
.
Вектор и направлен в сторону центра кривизны траектории.
Радиус кривизны траектории:
.
Траекторией движения точки является дуга параболы
; .
Скорость точки: .
Ускорение точки: ; ; .
Радиус кривизны траектории: .
Определение остальных величин
При решении задачи мы нашли:
вектор и модуль скорости:
; ;
вектор и модуль полного ускорения:
; ;
тангенциальное и нормальное ускорения:
; ;
радиус кривизны траектории: .
Определим остальные величины.
Единичный вектор в направлении касательной к траектории:
.
Вектор тангенциального ускорения:
.
Вектор нормального ускорения:
.
Единичный вектор в направлении главной нормали:
.
Координаты центра кривизны траектории:
.
Введем третью ось системы координат перпендикулярно осям и . В трехмерной системе
; .
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 22-02-2016 Изменено: 29-01-2020
По заданным уравнениям движения точки найти
Яблонский задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения.
По заданным уравнениям движения точки M установить вид ее траектории и для момента времени t=t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории. Необходимые для решения данные приведены в таблице 20.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 20) добавляется третье уравнение (табл. 22).
Общий порядок выполнения задания в этом случае такой же, как и в приведенном примере.
http://1cov-edu.ru/mehanika/kinematika/tochki/koordinatnyj-sposob-zadaniya-dvizheniya/
http://online-tusa.com/tasks/14289_1_11_0