Подвижные особые точки решений дифференциального уравнения

Особые решения дифференциальных уравнений

Решение дифференциального уравнения

называется особым , если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку кроме этого решения проходит и другое решение, имеющее в точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности . График особого решения будем называть особой интегральной кривой уравнения (1). Если функция и ее частные производные и непрерывны по всем аргументам , то любое особое решение уравнения (1) удовлетворяет также уравнению

Значит, чтобы отыскать особые решения (1), надо исключить из уравнений (1) и (2).

Полученное после исключения из (1) и (2) уравнение

Часто бывает так, что распадается на несколько ветвей . Тогда нужно установить, является ли каждая в отдельности ветвь решением уравнения (1), и если является, то будет ли оно особым решением, т.е. нарушается ли единственность в каждой его точке.

Пример 1. Найти особые решения дифференциального уравнения

а) Находим p-дискриминантную кривую. В данном случае и условие (2) принимает вид , отсюда . Подставляя это выражение для в уравнение (4), получаем

Кривая (5) есть p-дискриминантная кривая уравнения (4): она состоит из одной ветви — параболы.

б) Проверяем, является ли p-дискриминантная кривая решением заданного уравнения. Подставляя (5) и ее производную в (4), убеждаемся, что есть решение уравнения (4).

в) Проверяем, является ли решение (S) особым решением уравнения (4). Для этого найдем общее решение уравнения (4). Перепишем (4) в виде . Это уравнение Клеро. Его общее решение

Выпишем условие касания двух кривых и в точке с абсциссой :

Первое равенство выражает совпадение ординат кривых, а второе выражает совпадение угловых коэффициентов касательных к этим кривым в точке с абсциссой .

Полагая , находим, что условия (7) принимают вид

Подставляя в первое из равенств (8), получаем или т.е. при первое равенство выполняется тождественно, так как есть абсцисса произвольной точки.

Итак, в каждой точке кривой (5) ее касается некоторая другая кривая семейства (6), а именно та, для которой . Значит, есть особое решение уравнения (4).

г) Геометрическое истолкование.
Общее решение уравнения (4) есть семейство прямых (6), а особое решение (5) является огибающей этого семейства прямых (рис. 19).

Огибающей семейства кривых

называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства (9) и каждого отрезка которой касается бесконечное множество кривых из (9). Будем говорить, что кривые и касаются в точке , если они имеют в этой точке общую касательную.

Если (9) есть общий интеграл уравнения (1), то огибающая семейства кривых (9), если она существует, будет особой интегральной кривой этого уравнения. В самом деле, в точках огибающей значения совпадают со значениями для интегральной кривой, касающейся огибающей в точке , и, следовательно, в каждой точке огибающей значения удовлетворяют уравнению , т.е. огибающая является интегральной кривой.

Далее, в каждой точке огибающей нарушена единственность, так как через точки огибающей по одному направлению проходит, по крайней мере, две интегральные кривые: сама огибающая и касающаяся ее в рассматриваемой точке интегральная кривая семейства (9). Следовательно, огибающая является особой интегральной кривой.

Из курса математического анализа известно, что огибающая входит в состав C-дискриминантной кривой (коротко СДК), определяемой системой уравнений

Некоторая ветвь СДК заведомо будет огибающей, если на ней:

1) существуют ограниченные по модулю частные производные

где и — постоянные;

Замечание. Условия 1) и 2) лишь достаточны, а потому ветви СДК, на которых нарушено одно из этих условий, тоже могут быть огибающими.

Пример 2. Найти особые решения дифференциального уравнения

а) Находим C-дискриминантную кривую. Имеем , так что отсюда . Подставляя это значение в (14), получаем откуда

Это и есть C-дискриминантная кривая: она состоит из двух прямых и .

б) Непосредственной подстановкой убеждаемся, что каждая из ветвей СДК является решением уравнения (13).

в) Докажем, что каждое из решений (15) является особым решением уравнения (13). В самом деле, так как и , то на каждой ветви СДК имеем (предполагаем, что решение уравнения (13) рассматривается на отрезке

где — область допустимых значений .

Заметим, что на любой из ветвей СДК в области 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMRDQiiHowAFBoWFRoLFx3eb7ogAAAMZJREFUKM+1UksSwyAIVUHAX+T+p602mTYkdqZd1AUL5fk+4NzfjiQvv/QXwkz++/6kyblOYfXmMd4vNxglaF//xu0KEeJZdVYXkDFUbhaSDCDqDtDhO3ASgOypGJbMyVh4A3A8bBpQq1URM1exAEcTUHaF4R5ZzFQXDE+FuDIfET4AiqZFe+PykiQHYIbb8rAgTsAM3lvTjvc5DCVeORANFjSxbhfOqn6ux5wPICRojOf2fJ81Uscj+bmEUc5q4jKCXucmPQAaYQaRCPmIUQAAAABJRU5ErkJggg==» />, так дх что выполняется одно из условий (12). Значит, условия (11) и (12) выполняются, а, следовательно, прямые (15) являются огибающими парабол (14).

Итак, установлено, что каждое из решений (15) есть особое решение.

В вопросах отыскания особых решений оказываются полезными следующие символические схемы:

Схема (16) означает, что уравнение p-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места точек заострения (возврата);

3) — уравнение геометрического места точек прикосновения интегральных линий, причем множитель входит в в квадрате.

Схема (17) означает, что уравнение C-дискриминантной кривой может распадаться на три уравнения:

1) — уравнение огибающей;

2) — уравнение геометрического места узловых точек, причем множитель входит в в квадрате;

3) — уравнение геометрического места точек заострения, причем множитель входит в в кубе.

Не обязательно, чтобы для каждой задачи все составные части и фигурировали в соотношениях (16) и (17).

Из всех геометрических мест только огибающая есть особое решение дифференциального уравнения. Отыскание огибающей упрощается тем, что в схемы (16) и (17) она входит в первой степени.

В отношении других геометрических мест (точек заострения, узловых точек и точек прикосновения) требуется дополнительный анализ в каждом конкретном случае. То обстоятельство, что некоторый множитель входит в в квадрате (и совсем не входит в ) указывает на то, что здесь может быть геометрическое место точек прикосновения интегральных линий. Аналогично, если некоторый множитель входит в в квадрате (и совсем не входит в ), то здесь может быть геометрическое место узловых точек. Наконец, если множитель входит в в первой степени, а в — в третьей, то возможно наличие геометрического места точек заострения.

Пример 3. Найти особое решение дифференциального уравнения

Решение. Особое решение, если оно существует, определяется системой

где второе уравнение (19) получено из (18) дифференцированием его по . Исключив , получим p-дискриминантную кривую , которая распадается на две ветви

Подстановкой убеждаемся, что обе функции являются решениями уравнения (18).

Чтобы установить, являются ли решения (20) и (21) особыми или нет, найдем огибающую семейства

являющегося общим интегралом для (18).

Выпишем систему для определения C-дискриминантной кривой откуда, исключая , получаем , или и , что совпадает с (20) и (21). В силу того, что на линиях (20) и (21) условия (11) и (12) выполняются, заключаем, что линии и являются огибающими, а значит (20) и (21) есть особые решения заданного уравнения.

Интегральные кривые (22) суть параболы , а линии — огибающие этого семейства парабол (рис. 20).

Пример 4. Найти особые решения дифференциального уравнения

Решение. Дифференцируем (23) по

Исключая из (23) и (24), получим . Дискриминантная кривая есть ось ординат. Она не является интегральной кривой уравнения (23), но согласно схеме (16) может быть геометрическим местом точек прикосновения интегральных кривых.

Решениями уравнения (23) являются параболы и те гладкие кривые, которые можно составить из их частей (рис. 21).

Из чертежа видно, что прямая действительно есть геометрическое место точек прикосновения интегральных кривых уравнения (23).

Пример 5. Найти особые решения дифференциального уравнения

Решение. Найдем . Исключая из системы уравнений получаем

Преобразовав уравнение (25) к виду , находим его общий интеграл .

Найдем . Исключая из системы уравнений будем иметь

Итак, из (26) и (27) имеем

Множитель входит в p-дискриминант и в C-дискриминант в первой степени и дает огибающую, т. е. функция есть особое решение дифференциального уравнения (25). Непосредственной подстановкой убеждаемся, что действительно удовлетворяет уравнению.

Уравнение , входящее во второй степени в p-дискриминант и совсем не входящее в C-дискриминант, дает место точек прикосновения .

Наконец, уравнение , входящее в C-дискриминант во второй степени и совсем не входящее в p-дискриминант, дает место узловых точек (рис.22).

Пример 6. Найти особые решения дифференциального уравнения

а) Ищем p-дискриминантную кривую. Дифференцируя (28) по , получаем , откуда

Подставляя (29) в (28), найдем уравнение :

б) Ищем общий интеграл уравнения (28). Обозначив у’ через р, перепишем (28) в виде

Дифференцируя обе части (28) по и учитывая, что , будем иметь

Приравнивая нулю первый множитель , получаем (29), а соотношение дает

Исключая параметр из уравнений (31) и (32), найдем общее решение уравнения (28):

в) Находим C-дискриминантную кривую. Дифференцируя (33) по C, будем иметь

Подставляя (34) в (33), получаем уравнение .

Согласно символическим схемам (16) и (17) заключаем, что есть огибающая семейства полукубических парабол (33), а есть геометрическое место точек заострения (множитель входит в уравнение в кубе) (рис. 23). Подстановкой в уравнение (28) убеждаемся, что есть решение, а решением не является (при уравнение (28) не имеет смысла). Таким образом, решение есть особое (огибающая семейства интегральных линий).

Нелинейные дифференциальные уравнения второго порядка с алгебраическими подвижными особыми точками Остроумов Сергей Иванович

Данный автореферат диссертации должен поступить в библиотеки в ближайшее время
Уведомить о поступлении

480 руб. | 150 грн. | 7,5 долл. ‘, MOUSEOFF, FGCOLOR, ‘#FFFFCC’,BGCOLOR, ‘#393939’);» onMouseOut=»return nd();»> Диссертация — 480 руб., доставка 10 минут , круглосуточно, без выходных и праздников

240 руб. | 75 грн. | 3,75 долл. ‘, MOUSEOFF, FGCOLOR, ‘#FFFFCC’,BGCOLOR, ‘#393939’);» onMouseOut=»return nd();»> Автореферат — 240 руб., доставка 1-3 часа, с 10-19 (Московское время), кроме воскресенья

Остроумов Сергей Иванович. Нелинейные дифференциальные уравнения второго порядка с алгебраическими подвижными особыми точками : ил РГБ ОД 61:85-1/175

Содержание к диссертации

Глава 1. Алгебраические подвижные особые точки уравнения

1.1. Постановка задачи и вспомогательное преобразование. 21

1.2. Об уравнениях (I.I.I), не имеющих однопарамет-рического семейства алгеброидных решений 24

1.3. Об уравнениях СІ.І.І), имеющих в точке одно-параметрическое семейство алгеброидных решений. 27

1.4. Общий случай 36

Глава 2. Алгебраические подвижные особые точки уравнения (0.22)

2.1. Постановка задачи. 42

2.2. Решения со свойством (А) 43

2.3. Формальные решения со свойством (В) 45

2.4. Случай р = 5 , с0с*г) f 0 49

2.5. Случай р = -2 , Сесх).щО 65

2.6. Общий случай 70

Об уравнениях (I.I.I), не имеющих однопарамет-рического семейства алгеброидных решений

В простейших случаях все решения удается выразить через элементарные функции или представить в виде квадратур от элементарных функций. Однако такие случаи встречаются крайне редко. И до настоящего.времени решения многих дифференциальных уравнений не найдены, что сдерживает развитие ряда научных и технических задач из области исследования процессов, описываемых этими уравнениями. С другой стороны, и чисто теоретические исследования, выполненные в рамках дифференциальных уравнений, способствуют решению проблем из других отраслей науки и техники.

В конце прошлого века работы Э.Пикара и С.Ли привели к более глубокому пониманию структуры дифференциальных уравнений, позволили их классифицировать, предвидеть случаи, когда они интегрируются в квадратурах, установить ряд свойств, которые до того казались не связанными друг с другом. Все это способствовало возникновению в теории дифференциальных уравнений задачи изучения свойств функцийг определяемых дифференциальными-уравнениями, непосредственно по виду заданного уравнения независимо от интегрируемости последнего в элементарных функциях или.квадратурах.. Такой подход. характерен как для теории-устойчивости, основы которой заложил A.M.Ляпунов в работе «Общая задача об устойчивости движения», так и для качественной теории дифференциальных уравнений, развитие которой-во многом определила работа А.Пуанкаре «0.кривых, определяемых дифференциальными уравнениями». Этот же подход характерен и для аналитической теории дифференциальных уравнений.

Основная теорема аналитической теории дифференциальных уравнений — теорема Коши — при весьма общих предположениях гарантирует существование и единственность голоморфного решения дифференциального уравнения при заданных начальных условиях. Для доказательства этой теоремы Коши разработал несколько методов. В частности, для комплексной плоскости он применил разложение решения в ряд и метод мажорант. Голоморфное решение, построенное по Коши, можно рассматривать как элемент аналитической функции и, осуществив всевозможные аналитические продолжения этого элемента, получить полную аналитическую функцию (по Вейерштрассу).. Эту функцию и можно рассматривать как частное решение дифференциального уравнения, продолженное или на всю комплексную плоскость, или на максимально возможную естественную область существования решения. Однако построение полной аналитической функции крайне сложно. Метод же Коши не позволяет изучить особые-точки.решения, конфигурация и структура.которых на плоскости по сути и определяет решение.

Вопрос о поведении решений дифференциальных уравнений в окрестности особых точек впервые был поставлен Врио и Буке [51], считавшими особыми такие точки, в которых нарушается хотя бы одно из условий теоремы Коши существования и единственности решения. Фукс же [56 J особые точки решений дифференциальных уравнений разделил на два класса. неподвижные и подвижные. К неподвижным он относил те особые точки, которые можно определить по виду самого уравнения, например, особые точки коэффициентов, а к подвижным -особые точки решения, конфигурация и характер которых меняются при переходе от одного частного решения к другому, т.е. зависят от начальных условий. В настоящее время используется.термин «особые точки дифференциальных уравнений», который включает в себя как подвижные, так и неподвижные особые точки. Разделение же особых точек на подвижные и неподвижные носит условный характер, на что обратил внимание, в частности, и Н.П.Еругин [17]. В дальнейшем, придерживаясь классификации Фукса, в каждом случае будем указывать те точки комплексной плоскости, которые отнесем к подвижным.

Если уравнения имеют подвижные особые точки, то задача определения числа и конфигурации особых точек каждого частного решения становится очень сложной, поскольку неизвестно какие из частных решений имеют особые точки, сколько их у данного решения, как они расположены на плоскости, какова структура решения в окрестности каждой особой точки. Это обстоятельство подчеркивалось неоднократно еще Пикаром, Пуанкаре, Пенлеве и другими. Поэтому первые шаги в аналитической теории дифференциальных уравнений были сделаны в решении задачи выделения уравнений, не имеющих вообще подвижных особых точек. Такими уравнениями оказались в основном линейные, и те -ория линейных дифференциальных уравнений в настоящее время развита достаточно широко.

Об уравнениях СІ.І.І), имеющих в точке одно-параметрическое семейство алгеброидных решений.

Нелинейные дифференциальные уравнения, как правило, имеют подвижные особые точки. До сих пор нет достаточно эффективных способов определения числа и конфигурации подвижных особых точек частных решений нелинейных дифференциальных уравнений. Эта задача не решена в общем виде даже для самых простых по виду уравнений, на-пример, для приведенного уравнения Риккати: =х .+ acz) #

Одной из основных задач аналитической теории нелинейных дифференциальных уравнений [Г7, Bj является задача построения классов уравнений с.определенными, наперед заданными свойствами решений в окрестности подвижных особых точек, например, решения имеют только однозначные особенности, или только алгебраические и т.д., т.е. ставится задача классификации дифференциальных уравнений по характеру их подвижных особых точек.

В теории нелинейных дифференциальных уравнений первого порядка впервые вопрос об исследовании особых точек уравнений был по — о ставлен Врио и Буке [51 — 53]. Им же принадлежит первая, хотя и несовершенная, классификация уравнений и их решений по характеру особых точек самого уравнения.При исследовании алгебраического дифференциального уравнения вида Рс&,я) -0 они нашли случаи, когда все решения есть однозначные функции. Более общую задачу для такого уравнения решил Эрмит [61], выделив при этом уравнения, ре шения которых не имеют критических подвижных особых точек. Для по-линомиального относительно ос и ое уравнения Р(х ,х х) = 0 (0.1) с аналитическими по Z коэффициентами Фукс [55, 5б] установил условия отсутствия в решениях подвижных алгебраических особых точек. В настоящее время уравнения вида (0,1) с однозначными подвижными особыми точками называются уравнениями класса Фукса. Однако исследования фукса не исключали возможности существования в решениях трансцендентных особенностей или точек неопределенности. Относительно уравнения (0.1) -Пенлеве [84] доказал теорему, устанавливающую, что эти уравнения не имеют подвижных неалгебраических особенностей, чем и устранил.пробелы в исследованиях Фукса. Теорема Пенлеве вносит большие, упрощения в.аналитическую -теорию нелинейных дифференциальных, уравнений первого порядка, которая также развита достаточно глубоко. Для нелинейных- дифференциальных уравнений второго порядка подобной общей теоремы не может существовать, так как среди уравнений вида «-Rcx tx .x)_ (0.2) есть уравнения [80, 86, 89] с подвижными особыми точками типа существенно особых. Например, в f80j приведено уравнение с общим решением х С(з-ъ) а- Т) и точка х а есть подвижная — 7 критическая существенно особая точка.

Задачу классификации дифференциальных уравнений по характеру их подвижных особых точек можно понимать и так. Пусть задано множество дифференциальных уравнений. Выделить из этого множества . все уравнения, подвижные особые точки которых обладают определенными свойствами. Множества могут быть самой различной природы, например, множество уравнений вида (0.2) описывается рациональной функцией R Ы, , г) переменных, и эе. с коэффициентами по г. из класса аналитических функций. Среди различных задач, которые можно поставить для каждого достаточно широкого множества 2. дифференциальных уравнений второго порядка, можно выделить следующие: 1. Построить подмножество 2, 2 уравнений без подвижных особых точек. 2. Построить подмножество C2g « 2. уравнений с неподвижными критическими особыми точками. 3. Построить подмножество п?с э ) уравнений с неподвижными трансцендентными и существенно особыми точками. 4. Построить подмножество =, сг 2 уравнений с неподвижными существенно особыми точками. В дальнейшем подмножества Г2 м будем называть уравнениями класса М. Для уравнений (0.2) класс А , как отмечалось выше, включает все линейные уравнения, однако линейными уравнениями не исчерпывается. Особые точки аналитических функций разделяют обычно [і, 10, 62] на однозначные и многозначные, изолированные и неизолированные, и простейшими из них считаются изолированные однозначные особые точки типа полюсов. Поэтому естественно, что первые исследования в аналитической теории нелинейных дифференциальных уравнений вто — 8 рого порядка были направлены на то, чтобы построить классы уравнений с наиболее простыми подвижными особенностями. В работах Пи-кара [87, 88], Пенлеве 82, 83, 85], Гарнье [59, 60] , Гамбье [57, 58] и других авторов была решена задача построения класса В уравнений вида (0.2), если R Cx x,z)- рациональная относительно % и х функция с голоморфными в некоторой области коэффициентами по «г . (Эту задачу позднее стали называть задачей Пенлеве.) Задача Пенлеве разделяется на две части. Используя теорему Пуанкаре о разложении решений дифференциальных уравнений ліо.степеням малого параметра, Пенлеве разработал метод (метод малого параметра Пенлеве) отсеивания тех уравнений вида (0.2), которые заведомо имели неоднозначные подвижные особые точки, что позволило решить первую часть задачи, установив.тем самым необходимые условия принадлежности уравнений вида (0.2) классу В. Вторая часть задачи состояла в доказательстве отсутствия в выделенных уравнениях критических подвижных особых точек. Кроме того, было доказано, что выделенные уравнения не содержат трансцендентных и существенно особых точек. Таким образом, была установлена и достаточность построенной системы условий принадлежности уравнений вида (0.2) классу В .

Формальные решения со свойством (В)

Не так уж трудно дать некоторый аналитический смысл формальных решений, если не пытаться определить максимальную область существования, в которой формальное решение или сходится равномерно, или является асимптотическим представлением аналитического решения. Понятие асимптотического разложения впервые ввел Пуанкаре T93J, применив формулу Стирлинга для гамма-функций, и с помощью преобразования Лапласа доказал, что формальные степенные ряды есть асимптотические решения для линейных дифференциальных уравнений и -го порядка частного вида с иррегулярной особой точкой. В [96] доказано, что формальные степенные ряды всегда являются асимптотическими решениями и для общего случая. Асимптотическая теория линейных систем дифференциальных уравнений в основном завершена в Гб8] в том смысле, что сектор, являющийся областью существования формального решения, имеет наибольший открытый угол.

Метод, развитый в [6Q], без каких-либо существенных изменений можно применить для систем нелинейных дифференциальных уравнений вида (О.В). Что касается первой задачи существования решения, то этот метод распространяется немедлено и дает ответ на нее, а в изучении второй играет важную роль в работе [7Ї]. В работах 81, также изучались системы (0.13), но в [97J доказано только существование асимптотического разложения формального решения, а в [81J доказана и сходимость асимптотического разложения методом мажорантных функций, причем с большим числом произвольных постоянных и с большим углом сектора, чем в [97].

Основная цель всех авторов заключалась в том, чтобы построить аналитическое представление решения, зависящего от нескольких произвольных постоянных и существующего в полной окрестности точки z-0 или в секторе с вершиной в особой точке « = , а также изучить природу особой точки z-0 аналитической функции, определяемой через это аналитическое представление. В случае, когда решение стремится к бесконечности при z — О вдоль пути L , выбранного произвольно, возникают трудности определения аналитического выражения для такого неограниченного решения.

В работах (54, 63, 81, 90J было проведено обобщение теоремы Пуанкаре [91] на многомерный случай системы (0.14) при предположении, что если и С м) характеристических чисел матрицы 1 (0,0) лежат по ту же самую сторону, что и единица, относительно прямой, проходящей через начало координат в комплексной плоскости Л , а другие (т-к.) характеристических чисел находятся по другую сторону или на этой прямой, то решение зависит от К параметров и выражается через равномерно сходящийся (к+і) -кратный степенной ряд по и некоторых функций.

Эта же система (0.14) была изучена в [72]при дополнительном предположении, что одно и только одно характеристическое число матрицы Якоби h CQO) равно нулю. Если среди характеристических чисел имеются равные нулю или отсутствуют нулевые корни, то из классической теории имеем аналитическое представление решений системы (0.14), зависящее.от К .параметров. Случай Я -УУІ был изучен в . /»54, 92], а в /8І.Ш, 54, 90] этот результат был применен к случаю

Случай, когда все характеристические числа матрицы hxCD,0) равны нулю, рассматривался в [75J при специальном выборе вектор-функции h(x;0). Если же нулевых характеристических чисел больше, чем одно, но меньше, чем w, то невозможно построить аналитическое представление общего решения без выполнения некоторых специальных условий, так как в этом случае общее решение является неограниченным. В [76] и указаны такие случаи, когда существует возможность построения аналитического выражения общего решения, если матрица h .(Q0) есть особая.

Для систем двух уравнений Врио и Буке эту же задачу решали в [33, 35, 36, 73j. В [20] приведен обзор всех известных результатов относительно систем двух уравнений вида (0.14). При исследовании поведения.решений дифференциальных уравнений и систем в окрестности особых точек как в комплексной, так и в вещественной области многие авторы (см., например, [19 — 25, 37 — 42, 47 — 50j) переходили к системам вида (0.14). Поэтому системы (0.14) рассматривались и в вещественной области, где применялись сущест — 16 венно отличные от аналитических способы исследования. В частности, такие исследования проводились в (19, 36 — 38].

Основная задача второй главы — построение системы условий на коэффициенты уравнения (0.22), обеспечивающих существование в каждой точке «г0Є D однопараметрического семейства алгеброидных со свойством (В) решений -решается.с использованием способов исследований, развитых в первой главе. Построенная в этой главе система условий и описывает класс С уравнений.(0.22). Здесь.же показывается, что нарушение хотя бы одного из условий алгеброидности выводит соответствующее уравнение из класса С, и в этом смысле построенная система условий является необходимой для принадлежности выделенных уравнений классу С?. Таким образом во второй главе и решается первая часть обобщенной задачи Пенлеве для уравнений вида (0.22).

Реферат: Особое решение дифференциальных уравнений первого порядка

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

1. Задача Коши для дифференциального уравнения первого порядка

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀ ), удовлетворяющего начальным условиям у(х₀ ) = у₀ .

Теорема Коши . (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

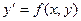Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х₀ , у₀ ) в области D, существует единственное решение уравнения , определенное в некотором интервале, содержащем точку х₀ , принимающее при х = х₀ значение j(х₀ ) = у₀ , т.е. существует единственное решение дифференциального уравнения.

1.1. Геометрический смысл

Геометрически речь идет о нахождении интегральной кривой, проходящей через заданную точку М (х ,у ).

Исключительно большое значение для теории дифференциальных уравнений и ее приложений имеет вопрос о существенности решения задачи Коши и о единственности этого решения. Будем говорить, что задача Коши

имеет единственное решение, если можно указать такую окрестность точки х