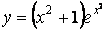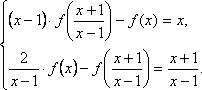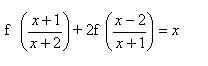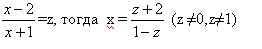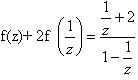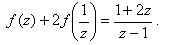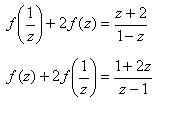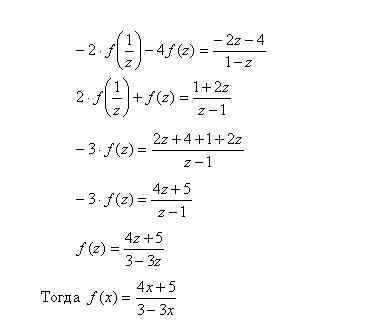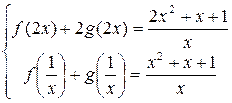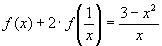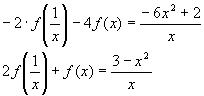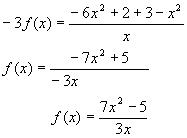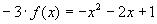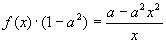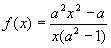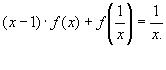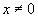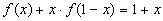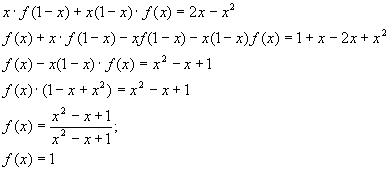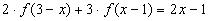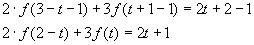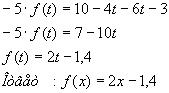Показать что функция u e xyz удовлетворяет уравнению
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        20.22. Показать, что функция y(x) удовлетворяет данному уравнению (1).
Электронная библиотека
Пример 1. Проверить удовлетворяет ли указанному уравнению данная функция z = f(x,y).
Решение. Находим частные производные первого и второго порядка:
Подставляем полученные значения производных в левую часть исходного уравнения:
В правой части уравнения имеем:
Сравнивая полученные результаты, видим, что данная функция удовлетворяет исходному уравнению.
Пример 2. Вычислить приближенно данные выражения, заменив приращения соответствующих функций их полными дифференциалами. Оценить в процентах возникающую при этом относительную погрешность вычислений.
Решение. а) Рассмотрим функцию
Значение этой функции в точке известно и равно
Вычислим приближенно значение функции по формуле:
Решение функциональных уравнений методом подстановки
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции, определённые на множестве 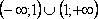
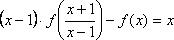
Решение:
Придадим x значение 

Отсюда 
Получим систему
Из уравнения (1) выразим 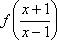
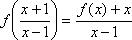
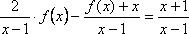
Отсюда 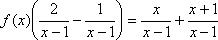


Проверим, действительно ли функция f(x) удовлетворяет уравнению 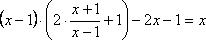
Ответ: 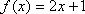
2. Найти функцию, удовлетворяющую уравнению
Решение:
2) Подставим в исходное уравнение, получим
3)Заменим z на 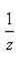
или после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
3.Пусть 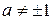

Решение:При замене
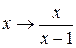

решением которой при a 2 ≠ 1 является функция
Ответ:
4.Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):
Решение:
В первом уравнении сделаем подстановку 2x = 1/z.
и первое уравнение принимает вид:
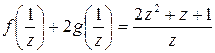
В результате получаем систему уравнений:
решение которой g(x) = 1/x, f(x) = x+1.
Ответ:g(x) = 1/x, f(x) = x+1.
5.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у. (1)
Решение:
Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х.
Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у ? R.
6.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у. (2)
Решение:
Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.
7.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению
f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)
Решение:
Поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (3) получаем f(х)= х 2 -х+1 .
Ответ: f(х)= х 2 -х+1.
8.Найдите все функции f: R à R, которые при всех х, у ? R удовлетворяют уравнению
f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (4)
Решение:
Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х 2 +6х+6)у=0 относительно х получаем х1= -1, х2= -5. Подстановка любого из этих значений в (4) дает нам f(у)=у 2 -4у.
9.Решите следующие функциональные уравнения.
в) f(x+y)+f(x-y)=2f(x)cos y
Решение:
а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.
б) Положим y=x-1/x , затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим
в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= — f(x). Заменив у на у+π/2, получаем
заменив теперь х- π/2 на х, имеем:
и с учетом предыдущего:
Положив х=0, получаем отсюда и из исходного уравнения:
Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.
10.
Решение: 1) Заменим 
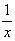
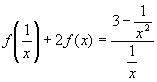

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
11. 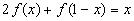
Решение: 1)Заменим в уравнении 
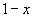
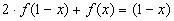
2) Умножим обе части исходного уравнения 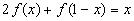
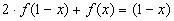
получим:
12.
Решение:
1) Заменим в уравнение 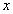
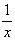
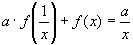
2)Умножим уравнение 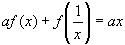

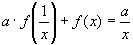
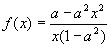
13.
Решение:
1)Заменим в уравнении 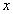
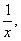
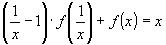
2)Выразим из исходного уравнения 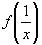
или 
3)Подставим 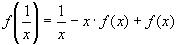
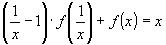

14.
Решение:
1.Заменим 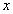
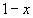
2.Умножим обе части уравнения 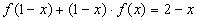

15.
Решение:1)Пусть 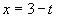
2)Пусть 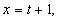
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
16.
Решение:
1) Заменим 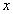
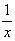
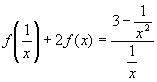

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
http://libraryno.ru/4-reshenie-tipovogo-varianta-funkneskperem/
http://megalektsii.ru/s5548t2.html