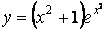Показать что функция удовлетворяет уравнению z arcsin xy

Показать что функция удовлетворяет уравнению z arcsin xy

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 20.22. Показать, что функция y(x) удовлетворяет данному уравнению (1).

&nbsp &nbsp &nbsp &nbsp &nbsp &nbsp &nbsp &nbsp (1)

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Глава 2. Функции комплексного переменного

Множества точек на плоскости

Рассмотрим некоторые вспомогательные геометрические понятия.

$|z|$ — расстояние от точки $z$ до начала координат;

$|z-z_0|$ — расстояние между точками $z$ и $z_0$;

$\$ — окружность с центром в точке $z_0$ и радиусом $R$;

$\^<\delta>(z_0)=\emptyset$, где $K_<0>^<\delta>(z_0): 0 1$ (внешность окружности) представляют собой односвязные области, так как имеют по одной границе.

2. Круговое концентрическое кольцо $D: r 0$, не является областью. Множество содержит точки, заполняющие I и III четверти. Множество является открытом, но нарушено свойство связности, так как точки из I и III четвертей нельзя соединить непрерывной линией, целиком состоящей из точек множества.

5. Кольцо $1 1$), то степень $\alpha^\beta$ имеет ровно $q$ различных значений. Во всех других случаях степень имеет бесконечное множество значений.

Обратные тригонометрические функции

Обратные тригонометрические функции также являются многозначными функциями. $$ \begin \mboxz=-\mathbf i \mbox(z+\sqrt), &\mboxz= -\mathbf i \mbox(\mathbf i z+\sqrt<1-z^2>), \\ \mboxz=-\frac<\mathbf i> <2>\mbox\displaystyle\frac<1+\mathbf i z><1-\mathbf i z>,&\mboxz=-\frac<\mathbf i> <2>\mbox\displaystyle\frac.\\ \end $$ При вычислении арккосинуса и арксинуса приходится извлекать квадратный корень из комплексного числа, то есть записывать два значения, для каждого из которых вычисляется логарифм. Для главного значения обратной тригонометрической функции выбирается то значение квадратного корня из комплексного числа, главное значение аргумента которого $\mbox\xi\in[0,\pi]$. Тогда все остальные значения будут получатся из главного по формуле: $$ \begin \mboxz=\pm\mboxz+2\pi k, k\in Z & \\ \mboxz= \pm\mboxz+2\pi k, k\in Z &.\\ \end $$

Предел и непрерывность функции

В дальнейшем мы будем рассматривать (если не будет специальной оговорки) однозначные функции. Если $w=g(z)$ — многозначная функция, то мы берем однозначную ветвь этой многозначной функции. Например, для $w=\mbox\,z=\mbox\,|z| + \mathbf i \mbox\,z+\mathbf i 2\pi k$ выбираем однозначные ветви: $$ w_0=\mbox\,|z| + \mathbf i \mbox\,z, \,\, w_1=\mbox\,|z| + \mathbf i \mbox\,z ++\mathbf i 2\pi, \dots $$

Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции вещественного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.

Пусть функция $w=f(z)$ определена и однозначна в некоторой окрестности $z_0$, исключая, может быть, саму точку $z_0$.

Конечная точка $A=a+\mathbf i b$ называется пределом функции $w=f(z)=u(x,y)+\mathbf i v(x,y)$ при $z\to z_0=x_0+\mathbf i y_0$, если действительные функции $u(x,y)$, $v(x,y)$ двух переменных $x$, $y$ стремятся соответственно к пределам $a$ и $b$ при $x\to x_0$, $y\to y_0$ $$ \lim\limits_<(x,y)\to(x_0,y_0)>u(x,y) = a, \quad \lim\limits_<(x,y)\to(x_0,y_0)>v(x,y) = b. $$ В этом случае пишут $\lim\limits_f(z)=A=a+\mathbf i b$.

Предел функции не должен зависеть от способа стремления $z$ к $z_0$.

Для комплексных функций имеют место свойства, аналогичные соответствующим свойствам для пределов вещественных функций. Если для двух функций $w_1(z)$ и $w_2(z)$ существуют пределы $B_1=\lim\limits_w_1(z)\neq\infty$, $B_2=\lim\limits_w_2(z)\neq0, \neq\infty$, то существуют пределы: \begin \begin &\lim\limits_(w_1(z)\pm w_2(z))=B_1\pm B_2,\\ &\lim\limits_(w_1(z)\cdot w_2(z))=B_1\cdot B_2,\\ &\lim\limits_\frac=\frac.\\ \end \end

Определение предела можно сформулировать также с помощью понятия окрестности (по Коши):

Если функция $w=f(z)$ определена в некоторой окрестности точки $z_0$ (но не обязательно в самой точке $z_0$) и если для любого $\varepsilon>0$ можно указать такое $\delta(\varepsilon)>0$, что как только точка $z$ попадет в $\delta$–окрестность точки $z_0$: $|z-z_0| 1) , определяем, что $u_x =3x^2-3y^2$, $v_x =6xy$, и, следовательно, сама $$ f'(z)=3x^2-3y^2+6\mathbf i xy=3(x^2+2\mathbf i xy-y^2)=3(x+\mathbf i y)^2=3z^2. $$

О т в е т: $f'(z)=3z^2.$

Аналитические функции

Функция $f(z)$ называется аналитической (или голоморфной, или регулярной) в конечной точке $z_0$, если она дифференцируема в каждой точке некоторой окрестности точки

Функция $f(z)$ однозначная и дифференцируемая в каждой точке области $D$ называется аналитической (иначе регулярной или голоморфной) в этой области.

Точки плоскости $z$, в которых однозначная функция $f(z)$ аналитична, называются правильными точками $f(z)$. Точки, в которых функция $f(z)$ не является аналитической, называются особыми точками этой функции.

Из определений видно, что понятие аналитичности и дифференцируемости в области совпадают,
в то время как условие аналитичности в точке является более жестким, чем условие дифференцируемости в точке.

Пример 1. Аналитической функцией является полином $$ P_n(z)=a_0z^n+a_1z^+\ldots+a_z+a_n,\quad a_0,a_1,\dots,a_n \in \mathbb C_<>, $$ так как он имеет производные во всех точках комплексной плоскости $z$.

Пример 2. Рациональная функция $$ R(z)=\frac, \quad P(z) \mbox < и >Q(z) \mbox< - полиномы>,$$ имеет производную в каждой точке, где $Q(z)\ne 0$. Поэтому $R(z)$ аналитична в области, полученной из плоскости $z$ удалением (выкалыванием) конечного числа точек, в которых $Q(z)=0$.

Пример 3. Функция $f(z)=z\cdot\bar$ не является аналитической ни в одной точке комплексной области. Условия Коши-Римана выполняются только в точке $z=0$, следовательно функция является дифференцируемой только в одной точке и не дифференцируема в окрестности этой точки.

Функция аналитическая во всей комплексной плоскости $ \mathbb C_<> $ называется целой функцией. Например, целыми являются функции $w=e^z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=\mbox\,z$, $w=z^n$, $w=P_n(z)$.

Связь аналитических функций с гармоническими

Пусть дана функция $f(z)=u(x,y) + \mathbf i v(x,y)$, аналитическая в некоторой области $D$. Тогда во всех точках области $D$ функции $u(x,y)$ и $v(x,y)$ удовлетворяют условиям Коши-Римана.

Выясним, любая ли функция двух переменных $x$ и $y$ может служить вещественной или мнимой частями некоторой аналитической функции.

Дифференцируя снова первое из условий по $y$, а второе по

Видим, что функции $u(x,y)$ и $v(x,y)$ должны удовлетворять одному и тому же дифференциальному уравнению с частными производными второго порядка, называемому уравнением Лапласа.

Функции, удовлетворяющие уравнению Лапласа, называются гармоническими функциями.

Функции $\varphi_1(x,y)$, $\varphi_2(x,y)$ удовлетворяющие уравнению Лапласа и условиям Коши-Римана называются взаимно сопряженными.

Итак, вещественная и мнимая часть аналитической функции являются сопряженными гармоническими функциями.

Гармонические функции встречаются во многих задачах физики и механики. Так, например, температура однородной пластинки, находящейся в тепловом равновесии, электрический потенциал плоского проводника, потенциал скоростей плоского установившегося потока однородной, несжимаемой жидкости и т.д. являются гармоническими функциями декартовых координат $x$ и $y$, т.е. удовлетворяют уравнению Лапласа, в соответствующих областях.

При решении многих задач механики и физики вместо того, чтобы искать гармонические функции и оперировать с ними, ищут аналитические функции, вещественными или мнимыми частями которых являются эти гармонические функции.

Восстановление аналитической функции по ее вещественной или мнимой части

Мы всегда можем построить аналитическую функцию (с точностью до постоянного множителя), для которой данная гармоническая функция является или действительной, или мнимой частью. Другую часть (мнимую или действительную) можно восстановить из условий Коши-Римана. Рассмотрим пример восстановления аналитической функции по ее заданной вещественной части, а потом запишем решение подобной задачи в общем виде.

Рассмотрим задачу: Восстановить аналитическую функцию $w=f(z)$, для которой данная функция $u=x^2-y^2+2x$ является вещественной частью.

1. Прежде всего надо помнить, что вещественная $u(x,y)$ и мнимая $v(x,y)$ части аналитической функции должны быть гармоническими, т.е. удовлетворять уравнению Лапласа.

2. Теперь найдем $v(x,y)$, используя условия Коши-Римана. $$ \frac<\partial u><\partial x>=\frac<\partial v> <\partial y>\,\, \Rightarrow $$ $$ v=\int\frac<\partial u> <\partial x>dy = 2xy+2y+C(x). $$ $$ \frac<\partial u><\partial y>=-\frac<\partial v> <\partial x>\,\, \Rightarrow $$ $$ -2y=-(2y+C'(x)) \,\, \Rightarrow C(x)=C_1\in \mathbb R_<>. $$ $$ v=2xy+2y+C_1. $$ $$ f(z)=u+\mathbf i y = x^2-y^2+2x +\mathbf i (2xy+2y+C_1)=z^2+2z+\mathbf i C_1. $$

Запишем решение задачи восстановления аналитической функции в общем виде.

Пусть дана гармоническая функция $u(x,y)$. Требуется найти $v(x,y)$, $f(z)=u+\mathbf i v$. Запишем условия Коши-Римана: $$ \frac<\partial v><\partial x>=-\frac<\partial u><\partial y>=P(x,y),\quad \frac<\partial v><\partial y>=\frac<\partial u><\partial x>=Q(x,y). $$ Составим полный дифференциал функции $v$: $$ dv=\frac<\partial v><\partial x>dx+\frac<\partial v><\partial y>dy=P(x,y)dx+Q(x,y)dy. $$ Он является полным, если $P’_y=Q’_x$, то есть $\displaystyle\frac<\partial^2 u><\partial x^2>+\frac<\partial^2 u><\partial y^2>=0$, что выполнено, так как данная функция $u(x,y)$ является гармонической. Тогда $$ v=\int\limits_<(x_0,y_0)>^ <(x,y)>P(x,y)dx+Q(x,y)dy+C, $$

$$ (x_0,y_0)\in D, \quad (x,y)\in D, $$ $$ f(z)=u(x,y)+\mathbf i v(x,y). $$ Так как дифференциал $dv$ — полный, то интеграл $\int\limits_<(x_0,y_0)>^ <(x,y)>Pdx+dy$ не зависит от пути интегрирования, если $D$ — односвязная область. При вычислении такого криволинейного интеграла удобно идти параллельно координатным осям. Например, сначала от точки $(x_0,y_0)$ вдоль оси $x$ до точки $(x,y_0)$, потом вдоль оси $y$ до точки $(x,y)$: $$ v(x,y)=\int\limits_^x P(x,y_0)dx+\int\limits_^y Q(x,y)dy +C= $$ $$ =-\int\limits_^x\frac<\partial u><\partial y>dx+\int\limits_^y \frac<\partial u><\partial x>dy +C. $$

Если дана гармоническая функция $v(x,y)$ и требуется найти аналитическую функцию $f(z)=u+\mathbf i v$, аналогично придем к криволинейному интегралу: $$ u(x,y)=\int\limits_<(x_0,y_0)>^<(x,y)>\frac<\partial v><\partial y>dx-\frac<\partial v><\partial x>dy +C. $$

Римановы поверхности

Риман предложил рассматривать многозначные функции комплексного переменного как однозначные функции на некоторых многолистных поверхностях.