Где — кратность корня характеристического уравнения. При этом в первом случае , а во втором случае
Замечание.Также в случае, когда правая часть уравнения имеет вид
и, 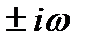
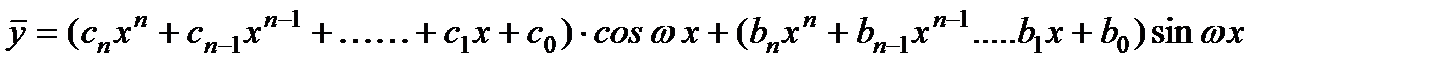
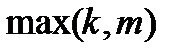
В том случае 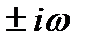
ЗАДАЧИ
1) Для заданных дифференциальных уравнений выписать характеристические уравнения и базисные решения (фундаментальную систему решений), записать общее решение однородного уравнения, 2) для неоднородных уравнений найти частное решение методом неопределенных коэффициентов (комплексных амплитуд), записать решение неоднородного уравнения, 3) при заданных начальных условиях найдите частное решение.
1) 
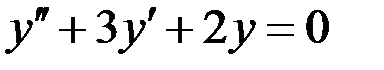
4) 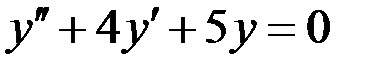
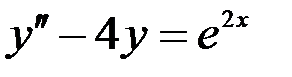
7) 
9) 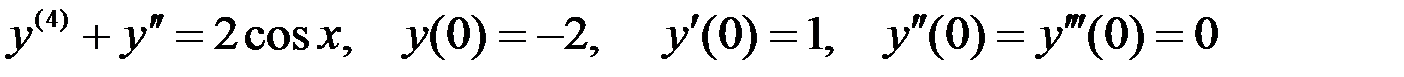
10.) 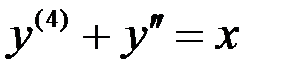
11).
Ответы : 9)
11)
12). Для уравнения затухающихколебаний
( x -координата, 

Для уравнения вынужденных колебаний
найдите частное решение методом комплексных амплитуд при условии, что 


Контрольные вопросы
1. Что является решением дифференциального уравнения?
Дайте определение общего и частного решений дифференциального уравнения
2. Сформулируйте теорему существования и единственности для дифференциального уравнения первого порядка
3. Определите тип дифференциального уравнения:
4. Решением дифференциального уравнения 
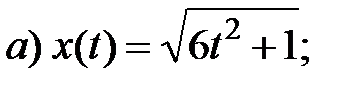
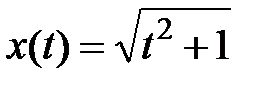
5. Дифференциальное уравнение семейства кривых 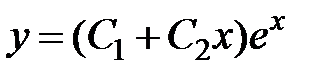
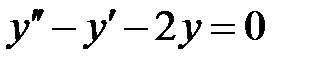
6. Частное решение дифференциального уравнения 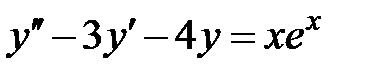
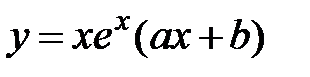
7. Корни характеристического 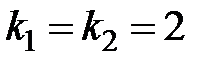
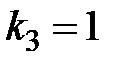
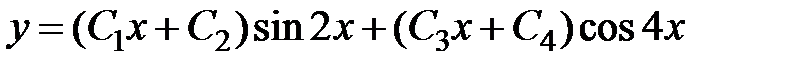
8. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
9. Из данных дифференциальных уравнений уравнениями c разделяющимися переменными являются…
Варианты ответов:
Должен быть указан не менее двух вариантов ответа
10. Дано дифференциальное уравнение 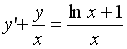
11. Общий интеграл дифференциального уравнения 
12. Общее решение дифференциального уравнения 
13. Решением уравнения первого порядка 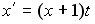
14. Общее решение дифференциального уравнения 
15. Общее решение дифференциального уравнения 
16. Общее решение дифференциального уравнения 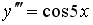
17. Общее решение дифференциального уравнения 
18. Общее решение дифференциального уравнения 
19. Общее решение линейного однородного дифференциального уравнения второго порядка 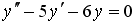
20. Однородному дифференциальному уравнению второго порядка 
21. Дано линейное однородное дифференциальное уравнение 
22. Дано дифференциальное уравнение 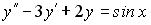
23. Методы приближенного решения дифференциальных уравнений.
РГР № 14 (0,600 ЗЕ)
Функции комплексной переменной
Срок выполнения 9- 13 недели
Содержание работы
1. Комплексные числа. Алгебраическая, тригонометрическая, показательная форма записи. Действия с комплексными числами
2. Функции комплексной переменной. Аналитические функции
3. Вычет аналитической функции в изолированной особой точке. Вычисление контурных и несобственных интегралов при помощи вычетов.
4. Ряды и преобразования Фурье.
5. Преобразования Лапласа.
6. Решение линейных дифференциальных уравнений и систем уравнений операторным методом.
7. Решение линейных дифференциальных уравнений методом свертки (формулы Дюамеля, Грина).
Литература [2, 3, 4, 11,16, 19]
1. Комплексные числа На множестве действительных чисел не существует такого числа, которое являлось бы корнем простейшего алгебраического уравнения 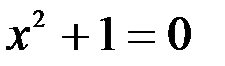 (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – (поскольку квадрат любого действительного числа неотрицателен). Поэтому возникла потребность расширить множество действительных чисел таким образом, чтобы новое множество содержало корни всех алгебраических уравнений. Введение комплексных чисел позволяет достигнуть этой цели. Прежде всего введем новый символ – 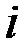 , который называют мнимой единицей таким образом, что , который называют мнимой единицей таким образом, что  . Тогда корни уравнения . Тогда корни уравнения 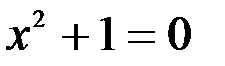 запишутся как запишутся как 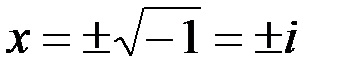 . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как . Алгебраическая форма записи комплексного числа Комплексное число в алгебраической форме записывается как 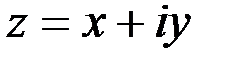 . Здесь . Здесь  – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: – действительное число, называемое реальной или действительной частью комплексного числа. Обозначают: 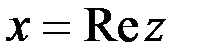 . Действительное число . Действительное число  называют мнимой частью комплексного числа. Обозначают: называют мнимой частью комплексного числа. Обозначают: 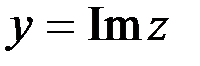 . Таким образом, комплексное число – это упорядоченная пара действительных чисел . Таким образом, комплексное число – это упорядоченная пара действительных чисел 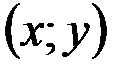 . Если . Если 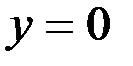 , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При , то комплексное число совпадает с действительным и изображается точкой на действительной оси ОХ. При  получаются чисто мнимые числа получаются чисто мнимые числа 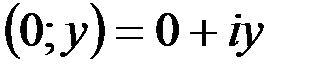 , которые изображаются точкой на мнимой оси OY. Комплексное число , которые изображаются точкой на мнимой оси OY. Комплексное число 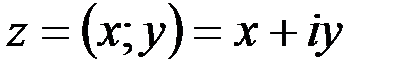 можно отождествить с точкой плоскости OXY или радиусом – вектором можно отождествить с точкой плоскости OXY или радиусом – вектором  . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: . Плоскость OXY будем называть комплексной плоскостью (рис. 1) Два комплексных числа равны, если равны их действительные и мнимые части: 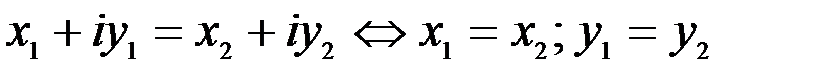 . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: . Два комплексных числа называют сопряженными, если действительные части этих чисел равны, а мнимые отличаются знаком. Обозначают: 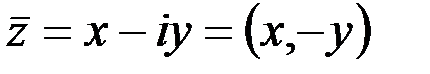 . Над комплексными числами в алгебраической форме определены следующие операции: . Над комплексными числами в алгебраической форме определены следующие операции: Сумма Разность Особо отметим произведение комплексно-сопряженных чисел, которое является числом действительным: Пример 1. Найти значение функции Второе слагаемое есть частное от деления двух комплексных чисел. Используя правило деления комплексных чисел в алгебраической форме, получим: Итак, Пример 2. Решить уравнение По формуле для корней квадратного уравнения имеем: Извлекая корень квадратный из числа источники: |
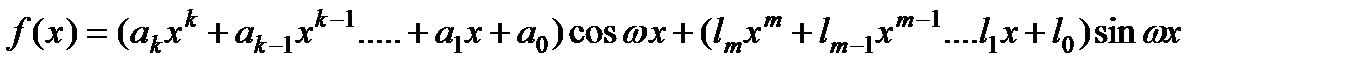
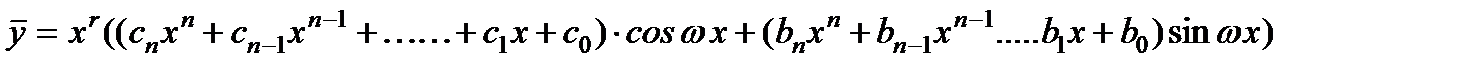
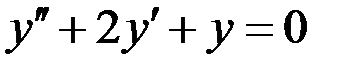
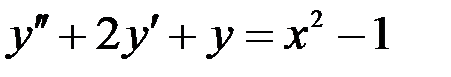
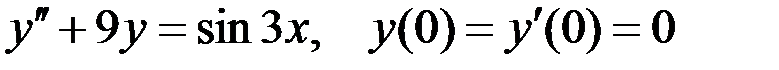


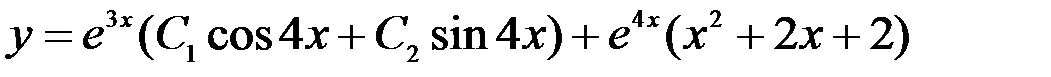

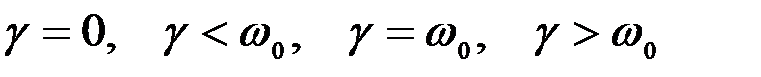
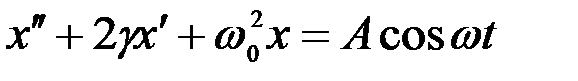
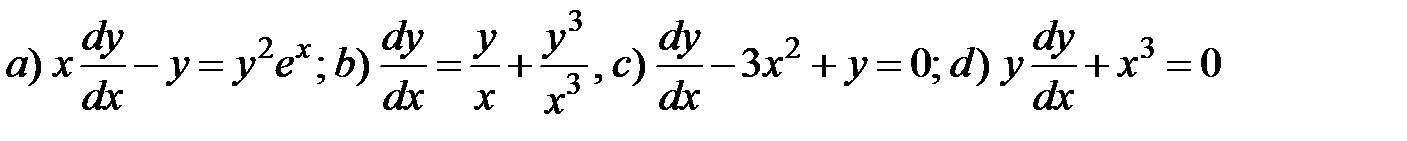
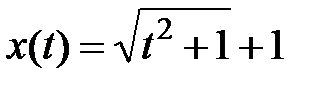
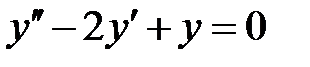


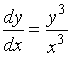
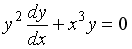
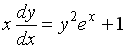
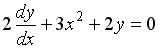
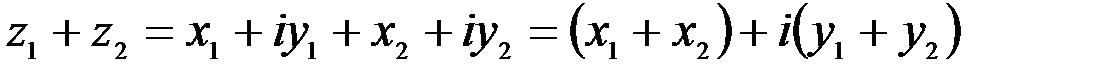 .
.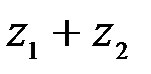 изображается вектором – суммой векторов
изображается вектором – суммой векторов 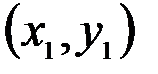 и
и  .
.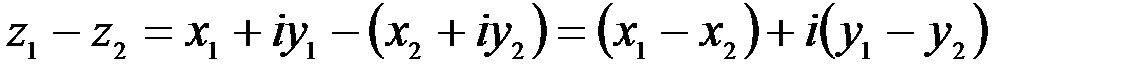 .
.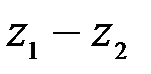 изображается вектором – разностью векторов
изображается вектором – разностью векторов 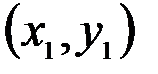 и
и 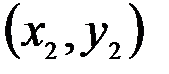 .
.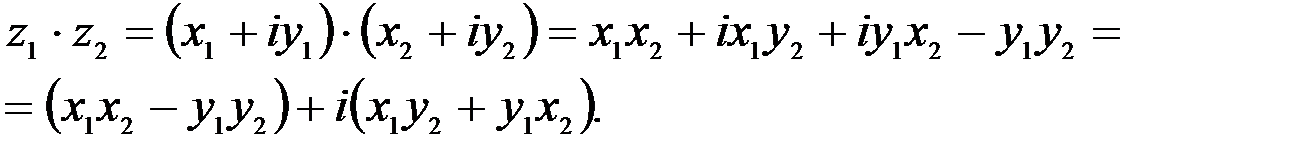
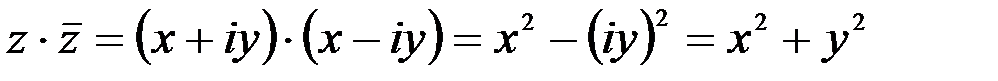 .
.
 при
при 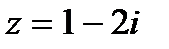 .
.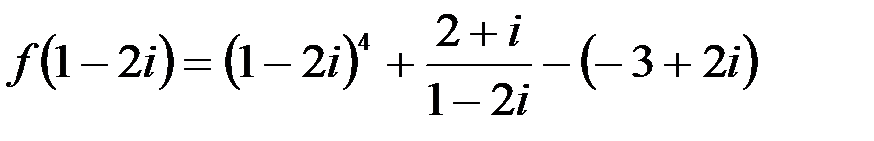 . Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
. Для вычисления первого слагаемого воспользуемся формулой бинома Ньютона:
 .
.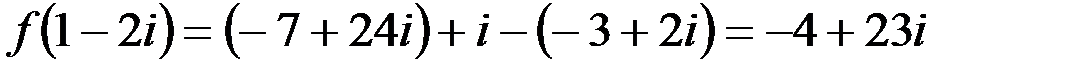 .
.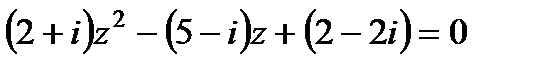 .
. .
. , получим:
, получим: 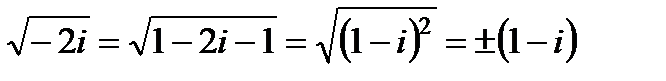 .
. . Отсюда
. Отсюда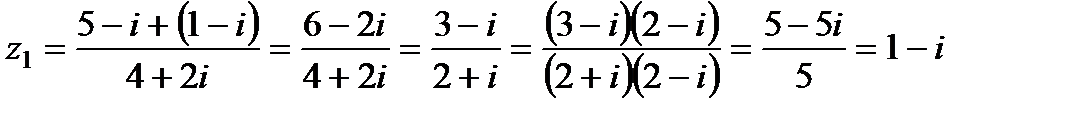
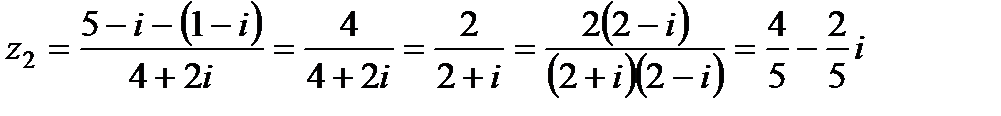 .
.