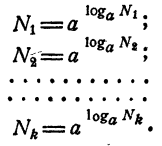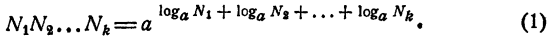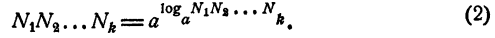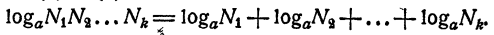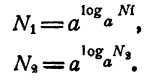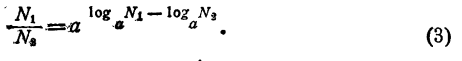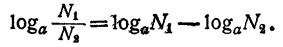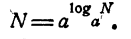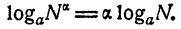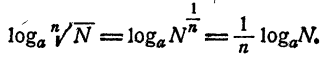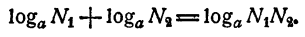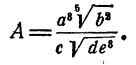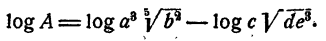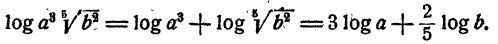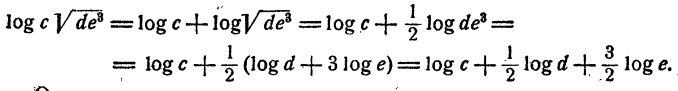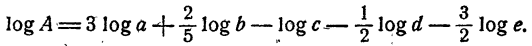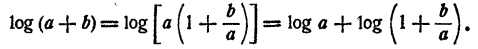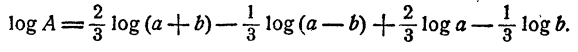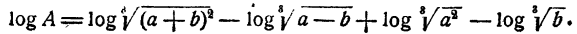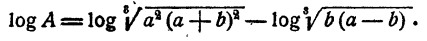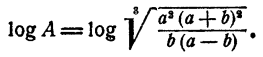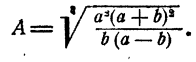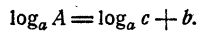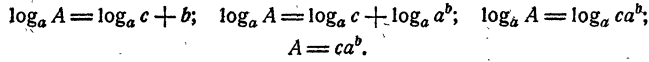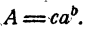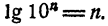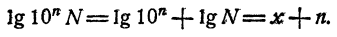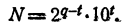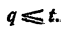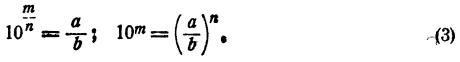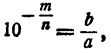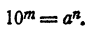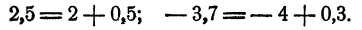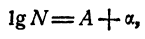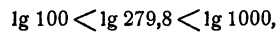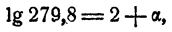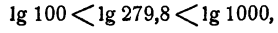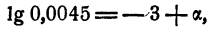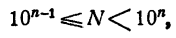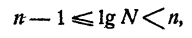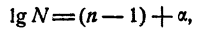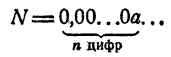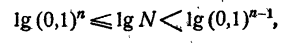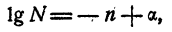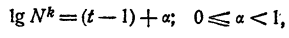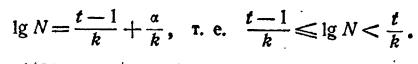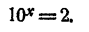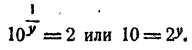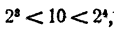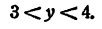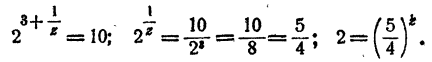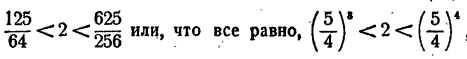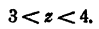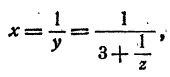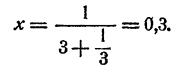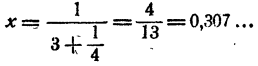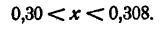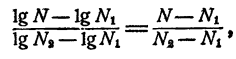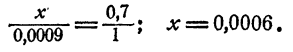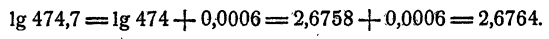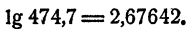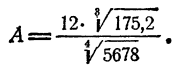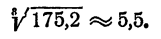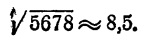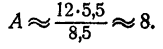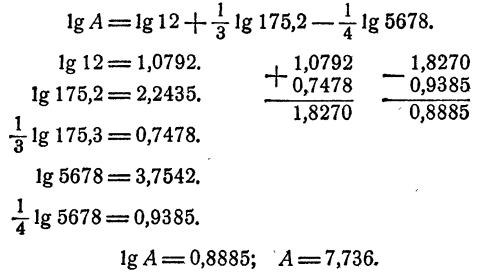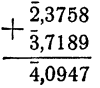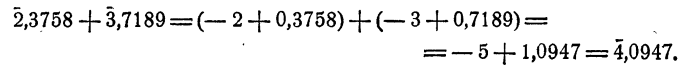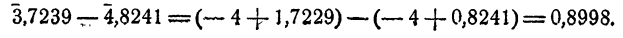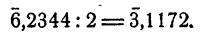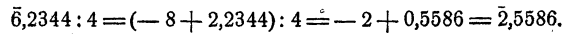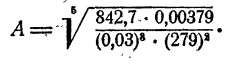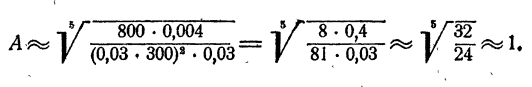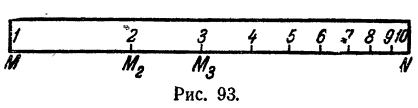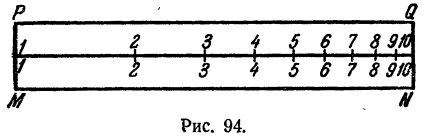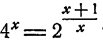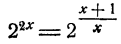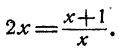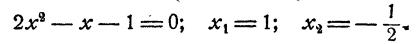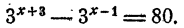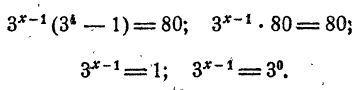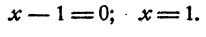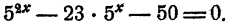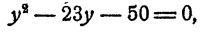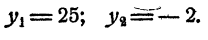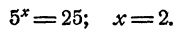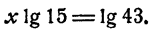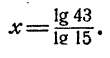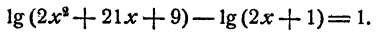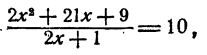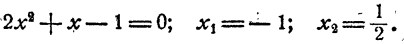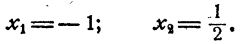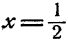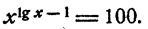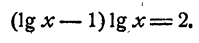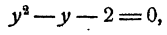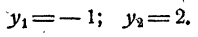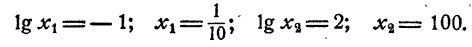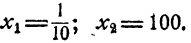Показательные функции и логарифмы в математике с примерами решения и образцами выполнения
Определение показательной функции:
Определение:
Показательной функцией от независимого переменного х называется выражение 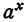
Если а положительно, функция 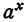
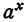
Если а отрицательно, функция 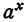
Если а = 0, функция 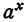
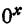
Свойства функции
- Если а > 0, функция
определена при всех значениях х от -∞ до +∞
- При всех значениях х функция
> 0
- При а > 1 функция
возрастает. При a х₂ . Тогда при
а при
Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция
неограниченно возрастает, а при неограниченном убывании показателя х функция
принимает значения, сколь угодно близкие к нулю.
Если a
Доказательство:
Пусть а > 1 и М—сколь угодно большое положительное число. Как показано в теореме 2 § 9 гл. V, 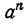
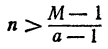
При всех значениях х, удовлетворяющих этому неравенству,
Пусть теперь m— сколь угодно малое положительное число. По доказанному найдется такое х, что 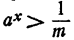
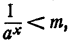
Первая часть утверждения доказана.
Пусть теперь а
убывает от значений сколь угодно больших до значений, сколь угодно близких к нулю. Вторая часть утверждения доказана.
6. Если а положительно и отлично от единицы, то каково бы ни было положительное число N, существует и притом только одно такое значение х, что
Иными словами, если а положительно и отлично от единицы и N— данное положительное число, уравнение 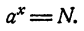
Доказательство:
Докажем сначала, что уравнение имеет решение. Одно из двух: или существует такое рациональное число г, что 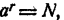
Пусть а > 1. Существует такое целое т, что 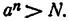

Рассмотрим последовательность степеней
Сравнивая члены последовательности (1) с числом N, можно найти такие два соседних члена 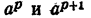
Составим теперь последовательность
Сравнивая члены последовательности (2) с числом N, можно найти таких два соседних члена 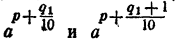
Сравнивая члены последовательности (3) с числом N, опять найдем таких два соседних члена 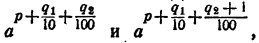
Продолжая неограниченно процесс деления промежутка на 10 равных частей и сравнивая всякий раз число N с получающимися при этом степенями числа а, получим две последовательности показателей
и две последовательности степеней
Последовательность (4) — возрастающая и ограниченная сверху любым членом последовательности (5). Последовательность (5) — убывающая и ограниченная снизу любым членом последовательности (4). Разность последовательностей (5) и (4) сходится к нулю. Следовательно, существует единственное число а, которое больше всех членов последовательности (4) и меньше всех членов последовательности (5).
Точно так же существует единственное число, которое больше всех членов последовательности (6) и меньше всех членов последовательности (7). Этим числом по построению последовательности является число N. По определению степени с иррациональным показателем, этим числом является 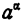
Пусть теперь а 1. Уравнение
имеет решение при любом положительном N. Это же решение удовлетворяет уравнению
Докажем, что решение единственно. Предположим, что уравнение имеет два решения: x = x₁, и х = х₂, причем x₁>x₂. Тогда имеем:
Но это невозможно, так как при
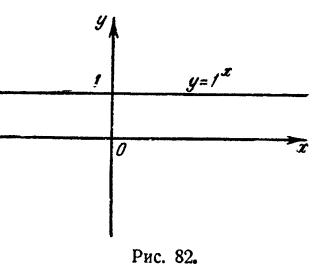
График показательной функции
Пусть а > 1, тогда график функции 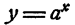
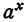
- Весь график расположен в верхней полуплоскости, т. е. там, где ординаты положительны (свойство 2 § 2).
- Всякая прямая, параллельная оси Оу, пересекает график и притом только в одной точке (свойства 1 и 4 § 2).
- Из двух точек графика правее, т. е. по мере продвижения слева направо график поднимается вверх (свойство 3 § 2).
- На графике имеются точки, лежащие выше любой прямой, параллельной оси Ох. На графике имеются точки, лежащие ниже любой прямой, проведенной в верхней полуплоскости параллельно оси Ох.
В левой своей части график, если наблюдать за ним справа налево, все ближе подходит к оси Ох, как бы стремясь коснуться ее. Однако график нигде не касается оси Ох (свойства 5 и 2 § 2).
5. Всякая прямая, параллельная оси Ох и лежащая в верхней полуплоскости, пересекает график и притом только в одной точке (свойство 6 § 2).
6. При всех а график проходит через точку (0,1). Это объясняется тем, что при любом положительном а
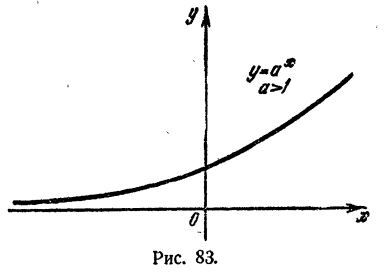
Если a 1 и при а
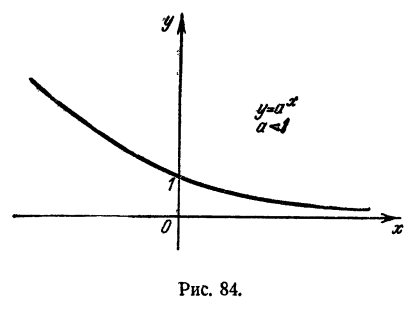
Таблица составлена посредством приближенного извлечения √2, ∜2, √8, ∜8 и т. д.
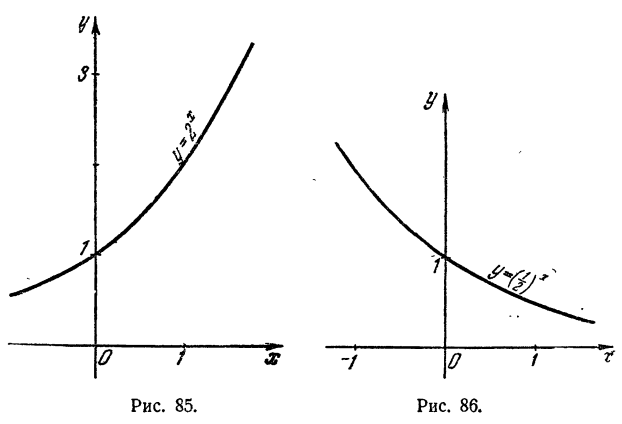
На рис. 86 изображен график функции 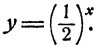
Определение логарифма
Определение:
Логарифмом числа N по основанию а называется показатель степени, в которую надо возвести а, чтобы получить N.
Для обозначения логарифма употребляется знак log. Тот факт, что число х является логарифмом числа N по основанию а, записывается так:
По определению 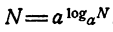
Логарифмическая функция
Пусть а > 0 и отлично от единицы. Возьмем произвольное положительное число у. Как показано (п. 6 § 2), уравнение
имеет единственное решение. Это значит, что всякое положительное число у по любому основанию (положительному и отличному от единицы) имеет единственный логарифм
Это утверждение называется теоремой о существовании логарифма.
Придавая числу у различные положительные значения, будем получать различные значения 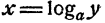
Логарифмическая функция 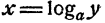
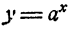
Показательная функция дает описание изменения степени числа а в зависимости от изменения показателя степени; логарифмическая функция дает описание изменения показателя степени в зависимости от изменения степени числа а.
Иными словами, показательная функция дает описание изменения числа в зависимости от изменения его логарифма по основанию а; логарифмическая функция дает описание изменения логарифма числа по основанию а в зависимости от изменения числа.
Таблица значений показательной функции при данном основании а является одновременно и таблицей значений логарифмической функции при том же основании а.
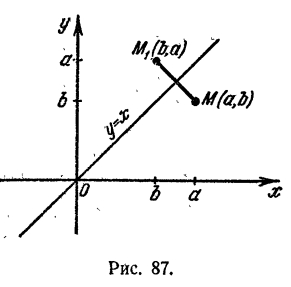
График показательной функции 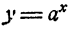
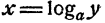
отложены на горизонтальной оси, а значения функции — на вертикальной; в другом случае, наоборот, значения функции отложены на горизонтальной оси, а значения не-, зависимого переменного — на вертикальной.
Показательная функция при основании а и логарифмическая функция при том же основании представляют пример двух обратных друг другу функций.
Обычно принято значения независимого переменного обозначать буквой х и откладывать на горизонтальной оси, а значения функции обозначать буквой у и откладывать на вертикальной оси.
Если придерживаться этого правила, то для функции 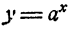
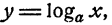
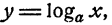
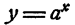
Свойства логарифмов чисел
Свойства логарифмов чисел при основании, большем единицы:
- Всякое положительное число имеет логарифм и притом только один. Это свойство вытекает из свойства 6 показательной функции.
- Отрицательные числа и число 0 не имеют логарифмов. Это свойство вытекает из свойства 2 показательной функции.
- Логарифм единицы равен нулю. Это вытекает из того, что при любом положительном а а⁰ = 1.
- Если
т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.
- Логарифмы чисел, больших единицы, положительны; логарифмы чисел, меньших единицы, отрицательны. Это вытекает из свойств 3 и 4.
- Если число растет неограниченно, то и логарифм его растет неограниченно. Если число, оставаясь положительным, стремится к нулю, логарифм его становится отрицательным и сколь угодно большим по абсолютной величине.
Это свойство вытекает из свойства 5 показательной функции и условно записывается так:
7. Логарифм основания равен единице.
Свойства логарифмов чисел при положительном основании, меньшем единицы:
- Всякое положительное число имеет логарифм и притом только один.
- Отрицательные числа и число 0 не имеют логарифмов.
- Логарифм единицы равен нулю.
- Бoльшее число имеет меньший логарифм.
- Логарифмы чисел, бoльших единицы, отрицательны; логарифмы чисел, меньших единицы, положительны.
(условная запись);
(условная запись)
- Логарифм основания равен единице.
Теоремы о логарифмах
Теорема:
Логарифм произведения двух или нескольких чисел равен сумме логарифмов сомножителей.
Доказательство:
Пусть 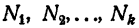
Перемножив эти равенства почленно, получим
С другой стороны, по определению логарифма,
Из равенств (1) и (2) имеем
Теорема:
Логарифм частного равен разности логарифмов делимого и делителя.
Доказательство:
Пусть N₁ и N₂ — произвольные положительные числа. По определению логарифма,
Разделив эти равенства почленно, получим
С другой стороны, по определению логарифма,
Из равенств (3) и (4) имеем:
Теорема:
Логарифм степени равен произведению показателя степени на логарифм основания.
Доказательство:
Пусть N—произвольное положительное число и а — любое вещественное число. По определению логарифма,
Возведя обе части равенства в степень а, получим
С другой стороны, по определению логарифма,
Из равенств (5) и (6) имеем
Теорема:
Логарифм корня равен логарифму подкоренного выражения, деленному на показатель корня.
Доказательство:
Пусть N — произвольное положительное число, n— натуральное. Тогда, используя теорему 3, получим
Доказанные теоремы служат основой для вычислений при помощи логарифмов.
Пусть требуется найти произведение двух чисел N₁ и N₂ Пользуясь графиком логарифмической функции или таблицей ее значений, определяют 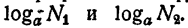
Остается по графику логарифмической функции или по таблице ее значений по 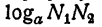
Точно так же при делении, возведении в степень и извлечении корня используются теоремы 2, 3, 4 соответственно.
Логарифмирование и потенцирование выражений
Пользуясь теоремами 1 —4 § 7, часто удается свести логарифм сложного выражения к результату простых действий над логарифмами входящих в него более простых выражений.
Такое преобразование логарифма называется логарифмированием выражения.
Например, пусть надо вычислить
Применяя теорему о логарифме частного, имеем
Далее, на основании теорем о логарифме произведения, степени и корня последовательно имеем
Таким образом, вычисление логарифма А сведено к вычислению логарифмов а, b, с, d, е.
Логарифм суммы не может быть просто выражен через логарифмы слагаемые. Иногда логарифм суммы преобразуется так:
Такое преобразование используется в так называемых гауссовых логарифмах.
При решении некоторых вопросов приходится ввести преобразование, обратное логарифмированию, т. е. приходится результат действий над логарифмами нескольких выражений преобразовывать в логарифм одного выражения. Такое преобразование логарифмов называется потенцированием выражения.
Пример:
Решение:
На основании теоремы о логарифме степени имеем:
На основании теоремы о логарифме произведения
Ha основании теоремы о логарифме частного
Так как из равенства логарифмов двух чисел дледует равенство этих чисел (см. свойство 4 § 6), то
Пример:
Найти А, если известно, что
Решение:
Ответ.
В этом параграфе, за исключением последнего примера, употребляется знак логарифма без указания основания, по которому берутся логарифмы. Объясняется это тем, что все изложенное здесь справедливо для логарифмов по любому основанию.
Десятичные логарифмы
За основание логарифмов обычно принимается число 10, так как 10 лежит в основе употребительной системы счисления. Логарифмы чисел по основанию 10 называются десятичными. Для упрощения записи десятичных логарифмов основание обычно не указывается и знак log заменяют знаком lg, т. е. вместо log₁₀N пишут lgN
Десятичные логарифмы обладают всеми свойствами логарифмов при основании, бoльшем единицы, и, кроме того, следующими:
- Если число является степенью 10 с натуральным показателем, то десятичный логарифм его равен количеству нулей в изображении этого числа. Действительно,
2. Если число является степенью числа 0,1 с натуральным показателем, то десятичный логарифм его равен целому отрицательному числу, абсолютная величина которого равна количеству нулей, входящих в десятичное изображение этого числа, в том числе и нуля целых.
Действительно, 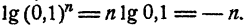
3. Если число умножить на 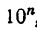
Действительно, пусть lg N = x, тогда lg
4. Если число разделить на 10ⁿ, логарифм его уменьшатся на n.
5. Если в десятичной дроби перенести запятую на п знаков вправо, логарифм ее увеличится на n. Если в десятичной дроби перенести запятую на п знаков влево, логарифм ее уменьшится на n.
6. Логарифмы рациональных чисел вообще иррациональны. Исключение составляют лишь числа, являющиеся степенью числа 10 с целым показателем.
Доказательство:
1. Пусть натуральное N имеет рациональный логарифм 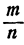
Если N делится на простое число р, отличное от 2 и 5, равенство (1) невозможно, так как 10ᵐ на р не делится. Остается предполагать, что 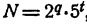
Равенство (1) принимает вид
Если m = nt равенство (2) невозможно, так как оно приводит к равенству
где q > t. Точно так же равенство (2) невозможно как при m nt. Итак,
Рассуждая точно так же, можно показать, что q не может быть меньше t.
2. Пусть N—неправильная несократимая дробь, т. е. 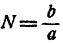
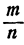
Так как степень несократимой дроби с натуральным показателем есть опять несократимая дробь, равенство (3) невозможно.
3. Пусть N — правильная несократимая дробь, т. е. 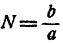
По доказанному в п. 2 равенство (4) возможно только тогда, когда b ≠ 1. Равенство (4) принимает такой вид:
По доказанному в п. 1 последнее равенство возможно только тогда, когда а есть степень числа 10 с целым неотрицательным показателем. Выходит, что
где k—целое неотрицательное число.
Характеристика и мантисса
Если действительное число не является целым, то его можно представить в виде суммы целого числа и положительного числа, меньшего единицы. Например,
Поэтому и логарифм любого положительного числа N можно представить так:
где А — целое число и 0 ≤ a
т. е. 2
где 0
т. е. —3
где 0
так как 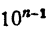
где 0 ≤ а
а — цифра, отличная от нуля. Тогда 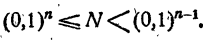
где 0 ≤ a Понятие о вычислении логарифмов
Для использования логарифмов при вычислениях необходимо, чтобы в распоряжении вычислителя имелись достаточно подробные таблицы значений логарифмической функции, вычисленные с определенной, достаточной для практических целей, точностью.
Математика располагает различными средствами для составления таких таблиц. Однако рассмотрение этих способов вычисления логарифмов выходит за пределы школьной программы.
Можно указать способ, далеко не совершенный, но весьма простой по идее, из рассмотрения которого будет видно, что логарифм любого натурального числа может быть вычислен с любой точностью.
Пусть требуется вычислить логарифм натурального числа N с точностью до 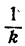
Например, 2¹⁰= 1024, значит, lg2¹⁰ = 3,… Отсюда lg2 = 0,3…
На следующем примере будет показан более совершенный способ вычисления логарифмов.
Пример:
Решение:
Обозначив искомый логарифм буквой х, имеем
Положим 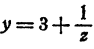
Дальнейшие вычисления по этой схеме затруднительны. Имеем
где 3
Положим z = 4, тогда
Так как 3
Посредством весьма несложных вычислений найдено значение lg2 с двумя верными знаками после запятой. Более точные вычисления показывают, что lg 2 = 0,30103 с точностью до 0,00001.
Интерполирование
Предположим, что логарифм числа N не указан в таблице. Найдем в таблице логарифмы ближайших к N чисел N₁ и N₂ из которых N₁ N Будем считать, что приращения логарифмов пропорциональны приращениям логарифмируемых чисел. Тогда имеем
откуда lgN легко определяется.
Этот способ приближенного вычисления, при котором по двум табличным значениям приближенно определяется промежуточное значение, называется интерполированием.
Пример:
Найти lg474,7, если lg 474 = 2,6758, a lg 475 = 2,6767.
Решение:
При увеличении числа на единицу логарифм его увеличился на 0,0009, так как 2,6767—2,6758 = 0,0009. На сколько увеличится логарифм, если число увеличится на 0,7? Предполагая, что приращения логарифмов пропорциональны приращениям логарифмируемых чисел, имеем
Таким образом, логарифм должен увеличиться на 0,0006, т. е.
Действительно, по пятизначным таблицам логарифмов видно, что
Мы получили правильный результат.
Употребление четырехзначных логарифмических таблиц
К таблицам логарифмов приложены объяснения, в которых показано, как следует пользоваться таблицами для отыскания логарифмов чисел и отыскания чисел по их логарифмам. Здесь поэтому нет надобности давать еще раз эти объяснения. Ограничимся рассмотрением примера. Пусть надо вычислить
Прежде всего следует, не вдаваясь в точные вычисления, определить, какой следует ожидать ответ. Так как 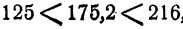
Так 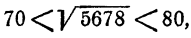
Мы видим, что ответ следует ожидать приблизительно равный 8.
Действия над логарифмами с отрицательными характеристиками
При вычислениях при помощи таблиц логарифмов часто приходится производить сложение и вычитание логарифмов, умножение логарифма на натуральное число, деление логарифма на натуральное число.
Эти действия производятся по обычным схемам с учетом незначительной особенности, вызванной тем, что характеристика логарифма может быть отрицательной.
Так как мантисса вычитаемого больше мантиссы уменьшаемого, к мантиссе уменьшаемого мысленно прибавляется единица, а от характеристики отнимается единица.
Если бы потребовалось 6,2344 разделить на 4, следовало бы к характеристике, прибавить —2, а к мантиссе + 2, т. е.
Пример:
Понятие об устройстве логарифмической линейки
Расскажем сначала, как при помощи двух линеек можно производить сложение и вычитание чисел.
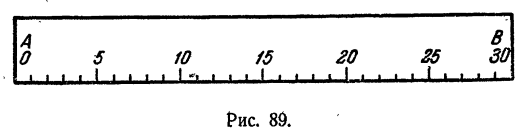
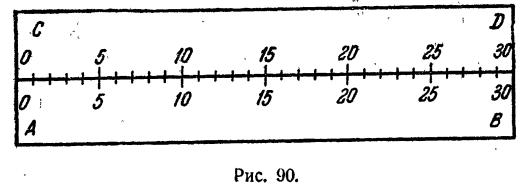
Возьмем линейку произвольной длины и разобьем ее делениями на 30 равных частей. У каждого деления поставим отметку 0, 1, 2,…, 30 (рис. 89).
Возьмем еще одну линейку такой же длины и разобьем ее на 30 равных частей так же, как и первую. Отметки на линейках должны быть расположены так, чтобы у одной из них они были нанесены на нижнем краю, а у другой —на ее верхнем краю (рис. 90).
При помощи этих двух линеек можно производить сложение и вычитание чисел.
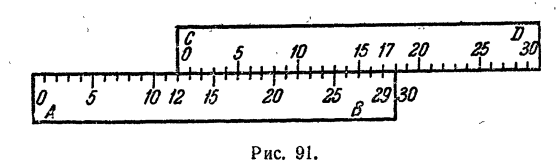
Предположим, что мы хотим к числу 12 прибавить число 17. Отметку 12 на линейке АВ поставим против отметки 0 на линейке CD. Затем найдем на линейке CD отметку 17 и прочтем противостоящую ей отметку 29 на линейке АВ. Эта отметка 29 и дает нам искомую сумму (рис. 91).
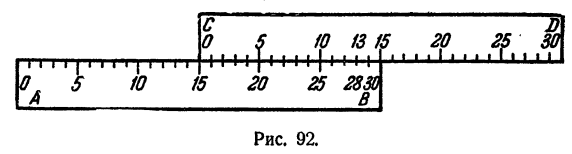
Точно так же производится вычитание. Предположим, что мы хотим от 28 отнять 13., Против отметки 28 на линейке АВ устанавливаем отметку 13 на линейке CD. Против отметки 0 на линейке CD находится отметка 15 на линейке АВ. Эта отметка 15 и дает нам искомую разность (рис. 92).
По такой же схеме ведутся вычисления и на логарифмической линейке. Различие лишь заключается в том, что при работе на логарифмической линейке складываются и вычитаются не числа, а их логарифмы.
Возьмем линейку MN произвольной длины и примем ее за единицу. У точки М поставим отметку 1, а у точки N—отметку 10. Это означает, что точка М изображает lg 1, а точка N изображает lg 10.
Отметку 2 мы ставим у точки М₂ находящейся от точки М на расстоянии приблизительно 0,3 MN. Это означает, что точка M₂ изображает lg 2 (lg 2 = 0,301).
Отметку 3 мы ставим у точки M₃, находящейся от точки М на расстоянии приблизительно 0,48 MN. Это означает, что точка М₃ изображает lg 3 (lg 3 = 0,477).
По этому же правилу ставим и остальные отметки. Получается линейка (рис. 93), на которой нанесена логарифмическая шкала.
Возьмем еще одну линейку такой же длины, как и MN, и нанесем на ней точно такую же шкалу, как и на MN. Отметки на линейках и здесь должны быть расположены так, чтобы у одной из них они были нанесены на нижнем краю, а у другой — на ее верхнем краю (рис. 94).
Из способа построения шкал на линейках МN и PQ вытекает, что сложение, произведенное при помощи линеек с логарифмическими шкалами, означает сложение логарифмов и, следовательно, может быть использовано для умножения чисел, логарифмы которых складывались.
Вычитание, произведенное при помощи линеек с логарифмическими шкалами, означает вычитание логарифмов и, следовательно, может быть использовано для деления чисел, логарифмы которых вычитались.
Из сказанного вытекают следующие правила умножения и деления чисел на логарифмической линейке.
Правило умножения. Для того чтобы при помощи двух одинаковых линеек МN и PQ с логарифмическими шкалами перемножить два числа тип, нужно на линейке МN отыскать деление с отметкой m и поставить это деление против отметки 1 или 10 на линейке PQ. Затем на линейке PQ отыскать деление с отметкой n и прочесть на линейке МN противостоящую отметку, которая и даст искомое произведение.
Правило деления. Для того чтобы при помощи двух одинаковых линеек с логарифмическими шкалами разделить число m на n, нужно отметку m на линейке МN поставить против отметки n на линейке PQ. Частное будет дано отметкой ла линейке МN, находящейся против отметки 1 или 10 на линейке PQ.
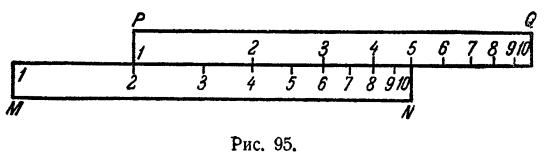
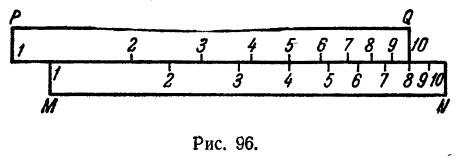
На рис. 95 показано умножение 2 на 3. На рис. 96 показано умножение 8 на 5. На этих же рисунках показано и деление 6 на 3 (рис. 95) и деление 40 на 5 (рис. 96).
Устройство логарифмической линейки изложено здесь очень кратко и только для того, чтобы помочь учащемуся сделать первые шаги для ознакомления с этим простейшим счетным прибором. Для того
чтобы научиться быстро считать на логарифмической линейке, нужно упражняться и попутно ознакомиться с подробным описанием линейки, и правилами ее использования.
Для приближенных вычислений логарифмическая линейка, длина шкалы которой 25 см, может заменить таблицы трехзначных логарифмов.
Решение некоторых трансцендентных уравнений
Мы рассматривали уравнения первой степени, квадратные, биквадратные, иррациональные. Все эти уравнения относятся к классу алгебраических уравнений.
Помимо алгебраических уравнений, рассматриваются уравнения неалгебраические, или трансцендентные.
Мы рассмотрим некоторые трансцендентные уравнения: уравнения, содержащие неизвестное в показателе степени (показательные уравнения), и уравнения, содержащие неизвестное под знаком логарифма (логарифмические уравнения).
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда
Так как степени числа 2 равны, то должны быть равны и показатели степеней
Проверка показывает, что оба решения удовлетворяют уравнению.
Пример:
Решить уравнение
Решение:
Допустим, что уравнение имеет решение. Тогда
Так как степени числа 3 равны, должны быть равны и показатели степеней
Проверка показывает, что найденное решение удовлетворяет уравнению.
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда, положив 5ᵡ = у, получим
Второе значение для у должно быть отброшено, так как 5ᵡ не может равняться отрицательному числу. Остается
Проверка показывает, что это решение удовлетворяет уравнению.
Пример:
Решить уравнение 15ᵡ = 43. ‘
Решение:
Это уравнение имеет единственное решение (свойство 6 показательной функции). Логарифмируя, имеем
Пример:
Решение:
Предположим, что уравнение имеет решение, тогда
Из равенства логарифмов двух чисел следует и равенство чисел
Итак, если рассматриваемое уравнение имеет решения то этими решениями могут быть только
Первое из этих значений не удовлетворяет уравнению, так как при х=- 1 под знаком логарифма оказывается отрицательное число.
Ответ.
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда логарифмы левой и правой частей должны быть равны:
Положим lg х = у. Имеем:
Оба значения неизвестного удовлетворяют уравнению.
Ответ.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной \(х\) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение \(х\). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо \(х\) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если \(х=3\), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны \(3\), только вот степени разные – слева степень \((4х-1)\), а справа \((-2)\). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что \(125=5*5*5=5^3\), а \(25=5*5=5^2\), подставим:
Воспользуемся одним из свойств степеней \((a^n)^m=a^
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить \(2\) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где \(a,b\) какие-то положительные числа. (\(a>0, \; b>0\).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит \(a^x\), с этим ничего делать не будем, а вот справа у нас стоит загадочное число \(b\), которое нужно попытаться представить в виде \(b=a^m\). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что \(16=2*2*2*2=2^4\) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 \Rightarrow 5^<-x>=5*5*5 \Rightarrow 5^<-x>=5^3 \Rightarrow –x=3 \Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 \Rightarrow (3*3)^<4x>=3*3*3*3 \Rightarrow(3^2)^<4x>=3^4 \Rightarrow 3^<8x>=3^4 \Rightarrow 8x=4 \Rightarrow x=\frac<1><2>.$$
Здесь мы заметили, что \(9=3^2\) и \(81=3^4\) являются степенями \(3\).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
\(3\) и \(2\) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число \(b>0\), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице \(a>0, \; a \neq 1\):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим \(2\) в виде \(3\) в какой-то степени, где \(a=3\), а \(b=2\):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: \(a^x=b\), где \(a>0; \; b>0\).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа \(a^x=b\), где \(a>0; \; b>0\). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что \(9=3^2\), тогда \(9^x=(3^2)^x=3^<2x>=(3^x)^2\). Здесь мы воспользовались свойством степеней: \((a^n)^m=a^
Обратим внимание, что во всем уравнении все \(х\) «входят» в одинаковую функцию — \(3^x\). Сделаем замену \(t=3^x, \; t>0\), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание \(3\). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член \(3=2+1\) и вынести общий множитель \(2\):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение \(t\):
Тут у нас две показательные функции с основаниями \(7\) и \(3\), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на \(3^x\):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену \(t=(\frac<7><3>)^x\):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену \(t=2^x\) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель \(2^x\)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании \(2\), \(5\) и \(10\). Очевидно, что \(10=2*5\). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой \((a*b)^n=a^n*b^n\):
И перекинем все показательные функции с основанием \(2\) влево, а с основанием \(5\) вправо:
Сокращаем и воспользуемся формулами \(a^n*a^m=a^
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Решение показательных и логарифмических уравнений в классах с углублённым изучениАем математики.
методическая разработка по алгебре (11 класс) по теме
Алгоритм решения показательных и логарифмических уравнений.
Скачать:
| Вложение | Размер |
|---|---|
| reshenie_pokazatelnykh_i_logarifmicheskikh_uravneniy_2.doc | 202.5 КБ |
Предварительный просмотр:
МОУ «Средняя общеобразовательная школа №22 с УИОП»
Решение показательных и логарифмических уравнений в классах с углубленным изучением математики.
Учитель математики Куликова Н.В.
Решению показательных и логарифмических уравнений в школьном курсе алгебры и начал математического анализа уделяется большое внимание, так как изучение этого вопроса открывает широкие возможности для четкого восприятия свойств функции, а также для повторения некоторых ранее изученных разделов алгебры (решение квадратных уравнений и т.д.)
Показательные уравнения принадлежат к классу уравнений, носящих название трансцендентных уравнений. Для этих уравнений нельзя указать общего способа решения. До окончательного решения трансцендентного уравнения неясно, сколько оно имеет корней. При решении показательных уравнений возможно получение посторонних корней, поэтому в тех случаях, где это необходимо, корни следует проверять подстановкой.
Показательные уравнения можно разбить на три типа, каждый из которых решается определённым способом.
К перовому типу можно отнести уравнения, в которых равные основания даны в неявном виде.
Исходное уравнение свелось к уравнению вида . Данное уравнение равносильно уравнению при условии, что и .
С учетом изложенного уравнение (*) равносильно уравнению
Необходимо сделать проверку, т.к. областью допустимых значений Х является не всё множество действительных чисел.
Можно разделить левую и правую части уравнения на произведение Это сделать можно, так как данное произведение не ровно 0 ни при каких Х.
Исходное уравнение свелось к уравнению . С учётом изложенного выше
Ко второму типу можно отнести уравнения, левая часть которых требует предварительного разложения на множители.
Степени равны, показатели степеней тоже равны при неравных основаниях, значит показатели степеней равны 0, т.е.
К третьему типу можно отнести уравнения, решение которых сводится к решению квадратного уравнения. При этом используется метод введения новой переменной с отбором корней на промежуточном этапе.
Если обозначить , ( по свойству показательных функций), то исходное уравнение сведётся к уравнению
не удовлетворяет условию .
В данном случае необходимости в проверке не существует.
Решение простейших логарифмических уравнений связано с определением логарифма и основным логарифмическим тождеством вида , где .
На основании определения логарифма решаются задачи, в которых по данным основаниям и числу определяется логарифм, по данному логарифму и основанию определятся число и по данному числу и логарифму определятся основание. Решения уравнений вышеприведенного характера обычно затруднений не вызывают. В школьной программе чаще всего встречаются уравнения, которые решаются либо непосредственным потенцированием, либо потенцированием с предварительным упрощением данного выражения, либо логарифмированием обеих частей уравнения.
Желательно, не приступая к решению уравнения, найти область допустимых значений функции, стоящей в левой части уравнения.
При наличии предварительного исследования проверку делать не обязательно. Если же исследование не проводится, то проверка решения необходима.
В данном случае
С учётом проведенного исследования проверка решения не нужна.
С учётом проведенных исследований возможно перейти к решению уравнения
Данное решение удовлетворяет ОДЗ, следовательно является корнем исходного уравнения.
Необходимо прологарифмировать обе части уравнения по основанию 10
Решив данное уравнение относительно , можно получить
С учётом ОДЗ является корнем исходного уравнения.
Логарифмирование обеих частей уравнения используется в основном для уравнений, в которых показатель степени содержит логарифмы.
Несколько примеров решения уравнений с усложнёнными условиями:
Естественно заметить, что , , . Используя определение логарифма, можно перейти к следующим равенствам:
Тогда с учетом новой переменной исходное уравнение примет вид
не удовлетворяет ОДЗ
Решив данное уравнение относительно , можно получить откуда
По теме: методические разработки, презентации и конспекты
Урок — семинар в 11 классе «Решение показательных и логарифмических уравнений с модулем»
Данный урок — семинар рекомендуется для работы в профильном классе, а также материал этого занятия можно использовать на факультативном занятии. Здесь предложен конспект урока, презентация, разадаточн.
Применение нестандартных способов при решении показательных и логарифмических уравнений и неравенств.
Разработка урока по теме «Применение нестандартных способов при решении показательных и логарифмических уравнений .
Урок алгебры в 11 классе с углубленным изучением математики по теме: «Решение показательных и логарифмических уравнений с переменным основанием. Введение сложной экспоненты».
Форма: урок-практикум.Задачи: путем введения сложной экспоненты научить решать показательные и логарифмические уравнения с переменным основанием.Цели урока:Образовательные: -.
Обобщающий урок по теме:»Решение показательных и логарифмических уравнений и неравенств» в 10 — 11 классе
Ребятам нравится практичесое приложение данного материала, спор двух очень сложных для решения и понимания функций (показательной и логарифмической).Решение большого количества различных заданий дает .
Урок алгебры в 11 классе «Решение показательных и логарифмических уравнений»
Презентация предназначена для проведения урока по алгебре (11 класс).Урок адресован:- учителям математики, работающим в выпускных классах, которым нужно не просто закрепить тему, но и подготовит.
Крупноблочное изучение тем : «Показательная логарифмическая функция», «Решение показательных и логарифмических уравнений и неравенств»
Данная методическая разработка поможеть учителю в планировании учебной деятельности.
Повторение 11 класс Решение показательных и логарифмических уравнений и неравенств
Рассматривается материал повторения решения показательных и логарифмических уравнений и неравенств.
http://sigma-center.ru/exponential_equations
http://nsportal.ru/shkola/algebra/library/2014/06/17/reshenie-pokazatelnykh-i-logarifmicheskikh-uravneniy-v-klassakh-s
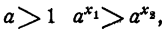 а при
а при 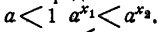 Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция
Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция 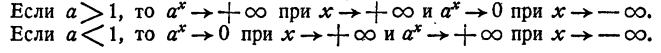
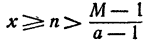
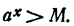
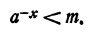
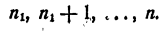


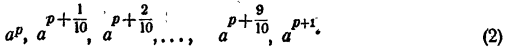
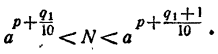
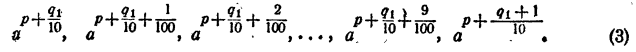
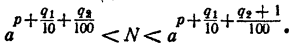
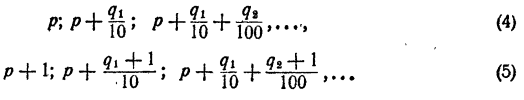
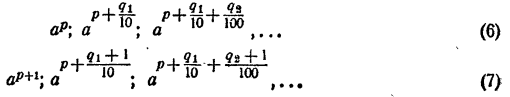
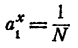
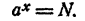
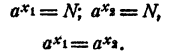
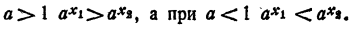

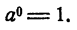
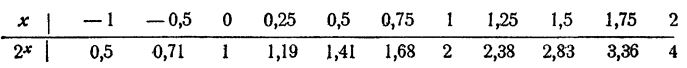
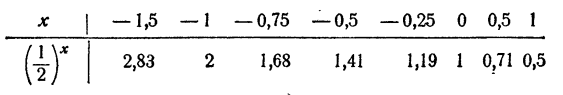
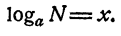
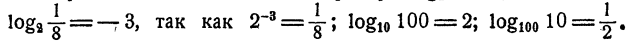
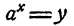
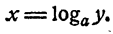
 т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.
т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.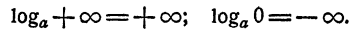
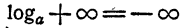 (условная запись);
(условная запись); 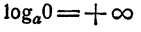 (условная запись)
(условная запись)