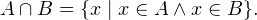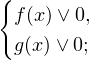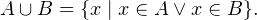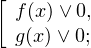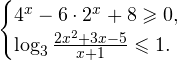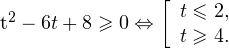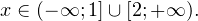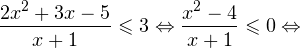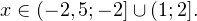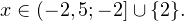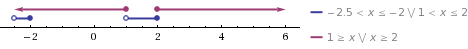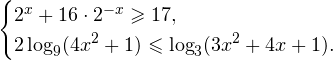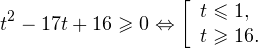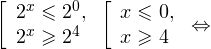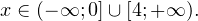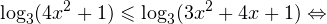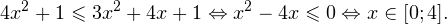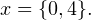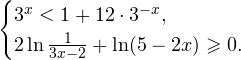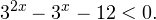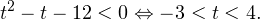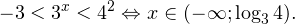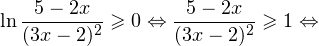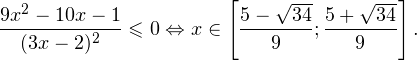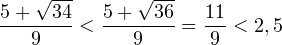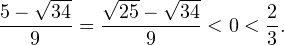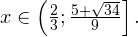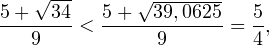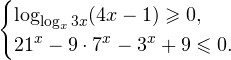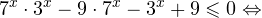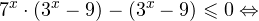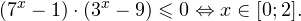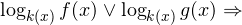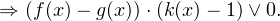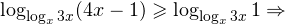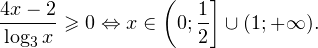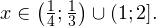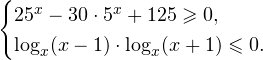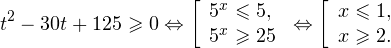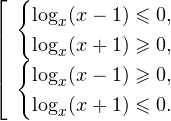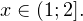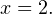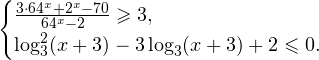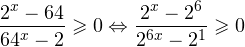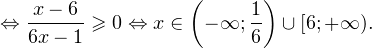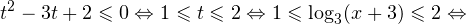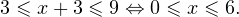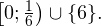Показательная и логарифмическая уравнения системы неравенства

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс Урок №44. Показательные и логарифмические уравнения и неравенства.

Перечень вопросов, рассматриваемых в теме

1) показательные уравнения и неравенства;

2) логарифмические уравнения и неравенства;

3) системы уравнений.

Глоссарий по теме

Показательными называются уравнения и неравенства, у которых переменная содержится в показатели степени.

Логарифмические уравнения и неравенства — это уравнения и неравенства, в которых переменная величина находится под знаком логарифма.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Вы уже умеете решать все виды уравнений и неравенств. Наша задача обобщить изученное, привести знания в систему. Начнем с показательных уравнений.

a х =b. где a>0, a≠1

Если b>0, уравнение имеет один корень: x=log_a b. График функции y=a x пересекает прямую y=b в одной точке.

Если b≤0 корней нет. График функции y=a x не пересекает прямую y=b.

При решении неравенств, обращаем внимание на основание. Если а>0, знак неравенства сохраняется. Если а 0, a≠1.

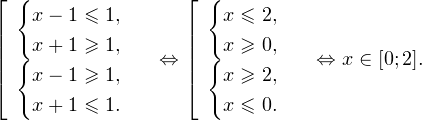
Логарифмическое уравнение log_ax=b имеет один положительный корень x=a b при любом значении b.

График функции пересекает прямую y=b в одной точке.

Уравнение имеет один положительный корень x=a b при любом b. График функции у= log_ax пересекает прямую y=b в одной точке.

При решении логарифмических неравенств обращаем внимание на область допустимых значений. Затем с учетом ОДЗ и значения решаем неравенство.

Теперь рассмотрим методы решения. Основных приема два: приведение к одинаковому знаменателю и замена переменной.

1 прием. Как в показательном, так и в логарифмическом уравняем основания. Затем сравним показатели или числа, стоящие под знаком логарифма.

2 прием. Замена переменных.

Находим корни и делаем обратную замену. При решении неравенств применяем те же самые приемы.

При решении логарифмических уравнений, возможно появление посторонних корней. Причина их появления — расширение области определения исходного уравнения. Поэтому проверка корней логарифмического уравнения осуществляется либо по области определения, либо непосредственной подстановкой найденных корней в исходное логарифмическое уравнение.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. Решить уравнение:

При х= -2 выражение lg(x-1) не имеет смысла, т.е. х=-2 посторонний корень. Ответ: х=2.

Пример 2. Найти значение выражения (х+у). x

Найдем область определения: х>0, у>0.

1. lg(xy)=lg100 ↔ xy=100 ↔ 2xy=200
2. сложим два уравнения: х 2 +2ху+у 2 =425+200=625 ↔ (х+у) 2 =625

Решение систем логарифмических и показательных неравенств с репетитором

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.

Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.

1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».

2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.

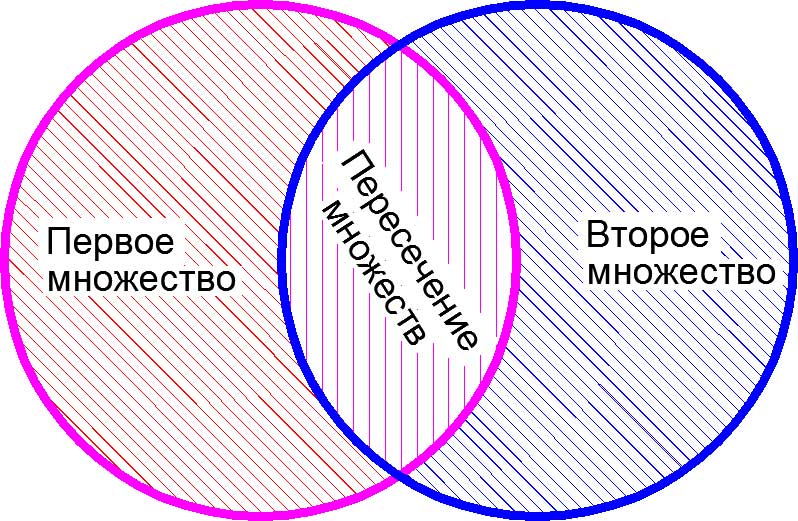
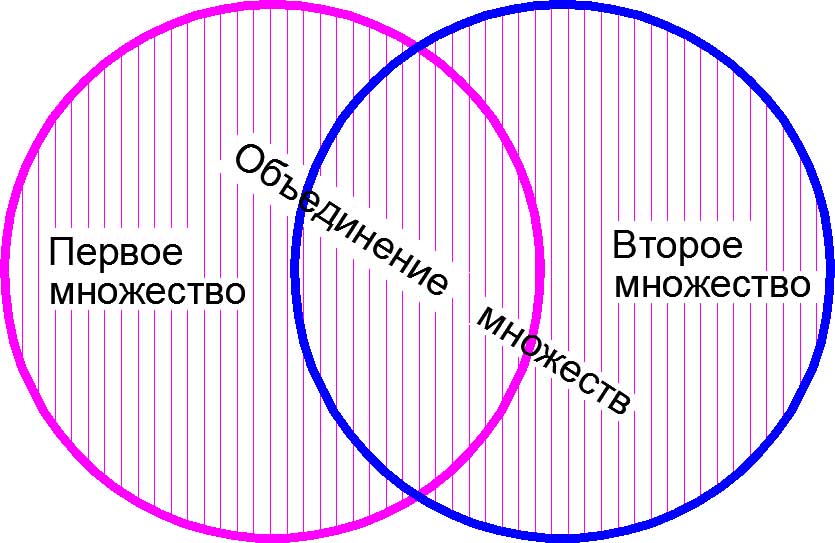
3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».

Другими словами, если даны два множества и то их пересечением будет являться множество следующего вида:

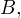
Изображение пересечения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из <ручки, карандаша, линейки, тетрадки, расчески>. У Алисы в сумочке находится «множество», состоящее из <записной книжки, карандаша, зеркальца, тетрадки, котлеты по-киевски>. Пересечением этих двух «множеств» будет «множество», состоящее из <карандаша, тетрадки>, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.

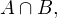
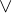
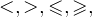
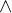
является промежуток то есть пересечение исходных промежутков. Здесь и далее под подразумевается любой из знаков ,\leqslant,\geqslant,» title=»Rendered by QuickLaTeX.com» height=»17″ width=»93″ style=»vertical-align: -4px;»/> а под — ему противоположный знак.

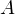
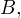
Другими словами, если даны два множества и то их объединением будет являться множество следующего вида:

Изображение объединения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из <ручки, карандаша, линейки, тетрадки, расчески, записной книжки, зеркальца, котлеты по-киевски>, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.

является промежуток 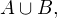то есть объединение исходных промежутков.

Перейдем непосредственно к примерам.

Решение задачи C3.

1. Решаем сперва первое неравенств. Используя замену 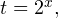переходим к неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством:

0\Leftrightarrow x\in(-2,5;-1)\cup(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

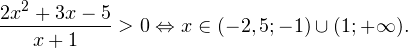
В области допустимых значений с учетом того, что основание логарифма 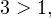1,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»52″ style=»vertical-align: -4px;»/> переходим к равносильному неравенству:

Исключая решения, не входящие в область допустимых значений, получаем промежуток

3. Ответом к системе неравенств будет пересечение полученных промежутков, то есть

Полученные промежутки на числовой прямой. Решение — их пересечение

Решение задачи C3.

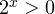
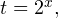
1. Решаем сперва первое неравенство. Умножаем обе части на 0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»55″ style=»vertical-align: 0px;»/> и делаем замену в результате чего приходим к неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

0, \\ 3x^2+4x+1>0\end\Leftrightarrow x\in(-\mathcal<1>;-1)\cup\left(-\frac<1><3>;+\mathcal<1>\right). \]» title=»Rendered by QuickLaTeX.com»/>

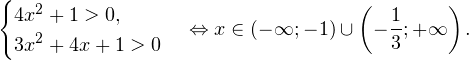
Воспользовавшись свойствами логарифмов, в области допустимых значений переходим к равносильному неравенству:

Данный промежуток целиком входит в область допустимых значений данного неравенства.

3. Общее решение системы будет являться пересечением полученных промежутков, то есть

Графическое изображение полученных промежуток. Решение системы — их пересечение

Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе его части на 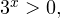0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»61″ style=»vertical-align: -4px;»/> после чего получаем неравенство:

Используя подстановку 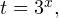переходим к следующему неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства:

0, \\ 5-2x>0 \end\Leftrightarrow \beginx>\frac<2><3>, \\ x

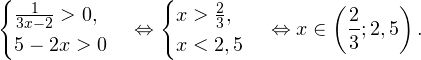
В области допустимых значений переходим к равносильному неравенству:

Обращаем внимание, что

Тогда с учетом области допустимых значений получаем:

3. Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как

\log_3\sqrt[4]<243>=\log_33^<\frac<5><4>> = \frac<5><4>, \]» title=»Rendered by QuickLaTeX.com»/>

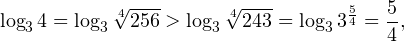
то 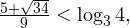и окончательный ответ к системе имеет вид:

Решение задачи С3.

1. Решим сперва второе неравенство:

2. Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства», в его основе лежит простая формула:

Вместо знака 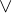может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:

Определим теперь область допустимых значений данного неравенства. Она задается следующей системой:

0, \\ \log_x 3x > 0, \\ \log_x 3x\ne 1, \\ x> 0, \\ x\ne 1\end\Leftrightarrow \beginx>\frac<1><4>, \\ \log_x 3x >\log_x 1, \\ x\ne 1, \\ x>0, \\ x\ne 1\end\Leftrightarrow \]» title=»Rendered by QuickLaTeX.com»/>

\frac<1><4>, \\ (3x-1)(x-1)>0 \\ x>0, \\ x\ne 1\end\Leftrightarrow x\in\left(\frac<1><4>;\frac<1><3>\right)\cup(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

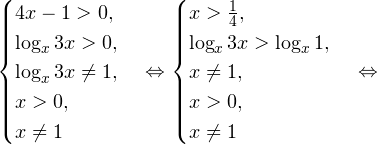
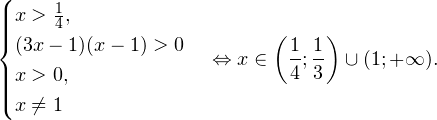
Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства.

3. Окончательным ответом исходной системы неравенств будет пересечение полученных промежутков, то есть

Решение задания C3.

1. Решаем сперва первое неравенство. Используем подстановку 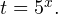Переходим к следующему квадратному неравенству:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

0, \\ x\ne 1, \\ x-1>0, \\ x+1 > 0\end\Leftrightarrow x\in(1;+\mathcal<1>). \]» title=»Rendered by QuickLaTeX.com»/>

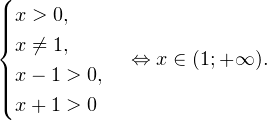
Данное неравенство равносильно следующей смешанной системе:

В области допустимых значений, то есть при 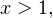1,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»53″ style=»vertical-align: -4px;»/> используя равносильные преобразования переходим к следующей смешанной системе:

С учетом области допустимых значений получаем:

3. Окончательным решением исходной системы является пересечение полученных промежутков, то есть

Изображение полученных промежутков на числовой прямой

Решение задачи C3.

1. Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду:

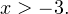
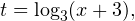
2. Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: -3.» title=»Rendered by QuickLaTeX.com» height=»14″ width=»68″ style=»vertical-align: 0px;»/> Используя замену переменной переходим к следующему квадратичному неравенству:

Этот ответ целиком принадлежит области допустимых значений неравенства.

3. Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств:

Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне.

Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека.

Практическая работа по теме: Показательные и логарифмические уравнения и системы уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Практическое занятие по теме : Решение уравнений и систем уравнений, содержащих натуральные и десятичные логарифмы и показательные выражения

Цель. Научиться решать уравнения и системы уравнений, содержащих натуральные , десятичные логарифмы и показательные выражения

Прочитать по учебнику темы «Логарифмы десятичные. Натуральный логарифм»Решение уравнений и систем уравнений

Выполнить самостоятельно практическую работу

1. Решение уравнений

1) Если показательное уравнение сводится к виду

где a > 0 и a ≠1, то оно имеет единственный корень х = b .

2)Иногда, чтобы привести показательное уравнение к виду (1), необходимо в левой части уравнения вынести за скобки общий множитель а х , например:

и т. д. Или разделить обе части уравнения на выражение, не равное нулю, к примеру:

и т. д..

3) некоторые показательные уравнения заменой а х = t сводятся к квадратным. Надо помнить, что t > 0, так как показательная функция не может принимать отрицательные значения.

Чаще всего при решении логарифмического уравнения его приводят к виду

Решив полученное уравнение, следует сделать проверку корней, чтобы исходное уравнение не потеряло смысл.

Рассмотрим решение примера № 377

Найти область определения функции (домашнее задание)

Y= log ₇ (5 – 2x); b) y = log ₂ (x 2 — 2x) ; c) у =ln(4 — x);

d ) у = ln ( 9 — x 2 )

Ответы: a ) b) ;

c )

На отрицательное число знак неравенства меняется на противоположный, т.е. x

b ) x 2 — 2x > 0 x (x — 2) > 0 x =0 u x =2 Применим метод интервалов:

b ) ;

c ) 4 – x >0 — x > — 4 (*-1) При умножении (делении) на отрицательное число знак неравенства меняется на противоположный, т.е. x

d ) 9 — x 2 > 0 x = — 3; x = +3

№ 337 (1) Решить уравнение.

log ₂ ( x – 5) + log ₂ ( x +2) = 3

Решение Используем свойство логарифмов. Представим число (3) как логарифм по основанию 2:

log ₂ ( x -5)( x + 2 ) = log ₂ 8 à ( x -5)( x +2) = 8 à x 2 – 3 x – 10 = 8 à .

à x 2 – 3 x — 18 = 0; x ₁ =- 3; x ₂ = 6.

Выполнив проверку, убеждаемся, что при x = — 3 log ₂ ( x – 5) и

log ₂ ( x +2) не имеют смысла

2 способ. log ₂( x -5)( x + 2 ) =3 ( x -5)( x +2)= 2 3 ;(по определению логарифма) ( x -5)( x +2) = 8 x 2 – 3 x – 10 = 8 x 2 – 3 x — 18 = 0; x ₁ = — 3; x ₂ = 6.

Ответ. х = 6. x ₁ = — 3: х > 5 u x > -2 х > 5

№ 337 (3) решить самостоятельно

Проверить решение по ранее записанного решения на обратной стороне доски или на слайде.

Решить уравнение: lg ( x — ) + lg ( x + ) = 0

Решение . lg ( x 2 – 3) = lg 1 à ( x 2 – 3) = 1 à x 2 = 4 à x ₁ =2; x ₂ = -2

Проверка при x = -2 lg ( x — ) u lg ( x + ) — не существуют или не имеют смысла

Решить следующие уравнения

1) 4 х+3 + 4 х =260; 2)

3) 4) 36 х – 2*18 х = 8* 9 х ;

5) log ₃ ( x 2 + 6) = log ₃ 5 x ; 6) log ₁₂ ( x 2 – x )=1;

7) log 2 _0,3 (x+1) – 4 log _0,3 (x+1) + 3 =0; 8) 9 x *3 x = 81

Решить системы уравнений

1.

Решить следующие уравнения 1) 9 х – 7*3 х = — 12; 2) 3) 4) 81 х – 2*9 х = 8* 3 х ;

5) log₅ (x 2 — 10) = log ₅ 9x; 6) log ₇ (x 2 + 6x)=1;

7) log _0,6 (x + 3) + log _0,6 (x — 3) = log _0,6 ( 2x — 1) ; 8 ) 25 x *5 x = 625

Дополнительно. Решить системы уравнений

1.

Работы собрать на проверку

Домашнее задание. Повторить определение логарифма и свойства показательных выражений и свойства логарифмов

Решение 1 варианта

4 х+3 + 4 х =260 4 х (4 3 + 1) = 260 4 х *65 = 260 (: 65) 4 х = 4 х=1

х 2 – 5 = 4х х 2 — 4х – 5 = 0 х₁= 5,х₂ = -1

2 x = t > 0

t ₁ = 4 u t ₂ = — 12 2 x = 4 x =2 Ответ. х=2

36 х – 2*18 х = 8* 9 х (4*9) х – 2*(2*9) х = 8* 9 х 9 х *(4 х – 2*2 x — 8) =0 тогда 4 х – 2*2 x — 8 = 0 2 x = t > 0 t 2 — 2 t — 8=0 t =4 u

t = — 2 тогда 2 x = 4 x = 2 Ответ. х= 2

5) log ₃ ( x 2 + 6) = log ₃ 5 x ; ОДЗ: х > 0 x 2 + 6=5 x x 2 — 5 x + 6=0 x ₁=2 u x ₂=3 Ответ. Х₁=2; x ₂= 3

6) log ₁₂ ( x 2 – x )=1 x 2 — x = 12 x 2 — x — 12=0 x ₁ = 4 u x ₂= — 3

ОДЗ: x 2 – x > 0; x ( x -1) > 0 x =0 u x =1

Ответ. Х₁ = 4 ;

x ₂ = — 3

7) log 2 _0,3 ( x +1) – 4 log _0,3 ( x +1) + 3 =0; log _0,3 ( x +1)= t — любое число, тогда

t 2 — 4t + 3=0t ₁ = 1 u t ₂ = 3

log _0,3 (x+1)=1x+1=0,3x₁= — 0,7; log _0,3 (x+1)=3x+1=0,3 3

8) 9 x *3 x = 81 3 3 x = 81 3 3 x =3 4 3 x =4 x =4/3.

Дополнительные задания(определяют можно ли работу оценить на 4 или на 5)

Решение 1 системы:

Ответ. (3,1) ОДЗ; (1;3) ОДЗ

Решение 2 системы:

_ОДЗ:

Ответ. х=8; у=2 ОДЗ (8>2*2)

Решение 2 варианта

1) 9 х – 7*3 х = — 12; 3 х = tt 2 — 7 t + 12=0 t ₁ = 3, t ₂= 4 3 x = 3;3 x = 4

x ₁ = 1; x ₂= log ₃ 4 Ответ. Х₁ = 1;. x ₂= log ₃ 4.

₂₎

₃₎

4 x = t

4) 27 х – 2*9 х = 8* 3 х ; 3 x (9 x — 2*3 x — 8)=0 3 x = t > 0 t 2 — 2 t — 8=0 t =4 u t = — 2 тогда 3 x = 4 x = log ₃ 4 Ответ. x = log ₃ 4.

5) log ₅ (x 2 — 10) = log ₅ 9x; x 2 — 9x — 10=0 x ₁ =10 u x ₂ =-1 x > 0

6) log ₇ ( x 2 + 6 x )=1; ( x 2 + 6 x )=7 x 2 + 6 x — 7=0 x ₁ = — 7 u x ₂ = 1

7 ) log _0,6 (x + 3) + log _0,6 (x — 3) = log _0,6 ( 2x — 1)

log _0,6 ( x + 3)* ( x — 3) = log _0,6 ( 2 x — 1) х 2 – 9 = 2х — 1 х 2 – 9 — 2х + 1=0

х 2 – 2х — 8 =0 х₁ = 4 и х₂ = — 2

ОДЗ: х+3 > 0, x – 3 > 0, 2 x -1 > 0 x > — 3, x > 3, x > 1/2 x > 3 х₁ = 4 и х₂ = — 2Ответ. Х₁ = 4 .

8 ) 25 x *5 x = 625 5 3x = 6255 3x =5 4 3x=4x=4/3. Ответ. Х= 4/3 .

Дополнительные задания(определяют можно ли работу оценить на 4 или на 5)

₁₎