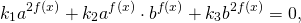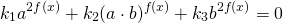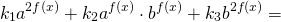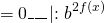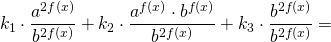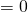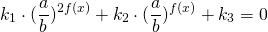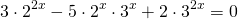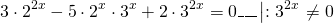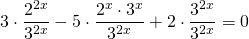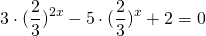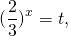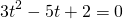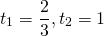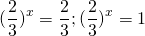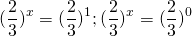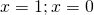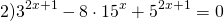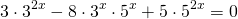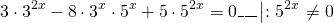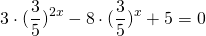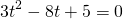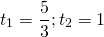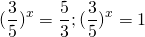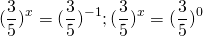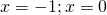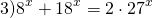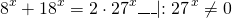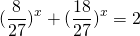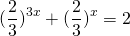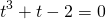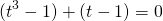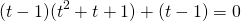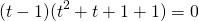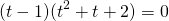Показательные однородные уравнения первой степени

Однородные показательные уравнения

Рассмотрим однородные показательные уравнения второй и третьей степени (1-й — здесь).

Однородное уравнение — это уравнение, все члены которого имеют одинаковую суммарную степень.

Однородные уравнения второй степени в общем виде можно записать так:

где k1, k2, k3, a и b — некоторые числа, причём a и b — положительны и отличны от единицы.

Чтобы прийти к такому виду, почти всегда уравнение требуется предварительно преобразовать. Чаще всего уравнение записывают в виде

Запишем признаки, которые позволят отличить однородное уравнение от уравнений другого вида.

Признаки однородного показательного уравнения второй степени

• уравнение содержит ровно три степени с разными основаниями;
• показатели двух степеней ровно в два раза больше показателя третьей степени;
• основание этой третьей степени равно произведению оснований двух других степеней.

Однородные показательные уравнения второй степени решаются почленным делением обеих частей на наибольшую из степеней.

0,\]» title=»Rendered by QuickLaTeX.com»/>

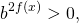
деление на степень не приводит к потере корней (то есть получаем уравнение, равносильное предыдущему).

ОДЗ: x∈R.Перепишем уравнение в виде

Разделим обе расти уравнения почтенно на 3 в степени 2x:

После упрощения приходим к уравнению

Это уравнение сводится к квадратному при помощи замены

где t>o. Оба корня квадратного уравнения

удовлетворяют условию t>0. Обратная замена

Сначала избавляемся от числовых слагаемых в показателях степеней, используя свойства степеней

представим степень с основанием 15 в виде произведения степеней с основаниями 3 и 5:

Делим обе части уравнения на 5 в степени 2x:

0,\]» title=»Rendered by QuickLaTeX.com»/>

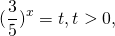
Оба корня положительны. Возвращаемся к исходной переменной:

По такому же принципу решаются однородные показательные уравнения 3-й степени.

o\]» title=»Rendered by QuickLaTeX.com»/>

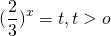
приводит к уравнению третьей степени

Представим -2=-1-1 и сгруппируем слагаемые

Общий множитель (t-1) вынесем за скобки

Получили уравнение типа «произведение равно нулю». приравниваем к нулю каждый множитель

Корень 1-го уравнения — t=1, второе уравнение не имеет корней. Обратная замена

Методы решения показательных уравнений

Показательные уравнения — определение

Показательными в алгебре называют уравнения с неизвестным, которое записано в показателе степени.

Простейшее показательное уравнение в теории имеет вид:

Здесь a > 0 , a ≠ 1 .

Пример формулы простейшего показательного уравнения:

При решении показательных уравнений многие математики советуют привести их к следующему виду:

После преобразования необходимо решить уравнение:

Виды показательных уравнений

Существуют разные типы показательных уравнений, как и неравенств. К примеру, самым простым из них является:

Знак перед b определяет количество корней показательного уравнения:

• при b ≤ 0 решения отсутствуют x ∈ ∅ ;
• когда b > 0 , x = log a b .

Показательным является уравнение в кратком виде:

В этом случае, неизвестная определяется таким образом:

1. При b ≤ 0 ⇒ x ∈ ∅ .
2. При b > 0 ⇒ f x = log a b .

Показательное уравнение может быть записано таким способом:

Данное уравнение является равносильным следующему уравнению:

Другой вариант записи показательного уравнения:

φ x f x = φ x g x

В этом случае возможны следующие решения:

• при φ x = 1 все части данного уравнения являются равными для каких-либо f x , g x ;
• при φ x > 0 , φ x ≠ 1 такое уравнение равносильно уравнению f x = g x ;
• при φ x = 0 уравнение равносильно f x > 0 , g x > 0 .

Записанное показательное уравнение является равносильным совокупности систем:

φ x = 1 , x ∈ R , φ x > 0 , φ x ≠ 1 , f x = g x , φ x = 0 , f x > 0 , g x > 0 .

Существуют показательные уравнения, которые допускается привести к квадратным. Как пример:

A · a 2 x + B · a x + C = 0

В этом случае A отлично от нуля, B и C являются какими-либо числами, a>0 и не равно единице.

В процессе решения подобных показательных уравнений требуется выполнить замену:

При этом t должно быть больше нуля. Получим:

A · a f x + B · a — f x + C = 0

Здесь A, B, a являются какими-либо числами, отличными от нуля. При этом а отлично от единицы, C определяется, как произвольное действительное число. Умножим все части уравнения на a f x > 0 , чтобы свести его к квадратному уравнению:

A · a f x 2 + B + C · a f x = 0

Выполним обратную замену a f x = t , t > 0 и запишем квадратное уравнение:

A t 2 + C t + B = 0

Следующим видом показательных уравнений являются однородные.

Однородные показательные уравнения первой степени являются такими уравнениями, которые записаны в виде:

Свести подобное уравнение к показательному a f x = b несложно. Достаточно обе части равенства разделить на a f x > 0 (или b f x > 0 ) :

a f x b f x = 1 ⇒ a b f x = 1 ⇒ f x = 0

Однородным показательным уравнением второй степени называют уравнение в виде:

A · a 2 f x + B · a f x · b f x + C · b 2 f x = 0

Подобные уравнения решают, согласно стандартному алгоритму. В первую очередь следует сократить обе части уравнения на a 2 f x > 0 , либо на b 2 f x > 0 . Таким образом, выражение примет следующий вид:

A · a 2 f x + B · a f x · b f x + C · b 2 f x = 0 , : b 2 f x > 0

A · a 2 f x b 2 f x + B · a f x · b f x b 2 f x + C = 0

A · a b 2 f x + B · a b f x + C = 0

Если заменить a b f x = t , где t больше нуля, то получится квадратное уравнение:

A t 2 + B t + C = 0

Метод решения показательных уравнений через приведение к одинаковому основанию

В процессе решения показательных уравнений a x = b обычно b заменяют какой-то степенью числа а. В результате уравниваются основания. Важно правильно определить общий множитель, и решение значительно упроститься.

При идентичных основаниях, но отличающихся показателях степени, умножение чисел предполагает сложение степеней, а в процессе деления степени вычитаются.

Рассмотрим правило на примере решения показательного уравнения, содержащего корень:

Заметим, что для чисел 64 и 8 общим множителем является число 2. Запишем степени:

Подставим полученные значения и преобразуем уравнение:

( 1 2 12 ) — x = 1 2 3

1 2 — 12 x = 1 2 2 3

( 1 2 ) — 12 x = ( 1 2 ) 2 3

В результате получилась дробь.

Попробуем решить следующее показательное уравнение. Здесь будет преобразована каждая часть выражения:

( 0 , 5 ) x 2 × 4 x + 1 = 64 — 1

Вычислим, каким должно быть общее основание:

0 , 5 = 1 2 = 2 — 1

В результате получим:

( 2 — 1 ) x 2 × ( 2 2 ) x + 1 = ( 2 6 ) — 1

2 — x 2 × 2 2 x + 2 = 2 — 6

2 — x 2 2 x + 2 = 2 — 6

— x 2 + 2 x + 2 = — 6

Заметим, что для данного показательного уравнения имеется пара решений: -2 и 4

Метод решения показательных уравнений через приведение к одинаковой степени

Не всегда при решении показательных уравнений получается использовать предыдущий метод. В некоторых случаях можно упростить задачу с помощью преобразования показателей степени. Данная методика имеет место лишь в том случае, когда в выражении используются операции умножения или деления.

Умножить числа, которые отличаются основаниями, но имеют идентичные степенные показатели, можно путем умножения лишь оснований. Степень при этом не меняется:

a x b x = ( a b ) x

Потренируемся использовать записанное правило. Решим пример:

5 2 x — 4 = 49 2 — x

В этом случае можно заметить отсутствие общих множителей в обеих частях выражения. Это не позволит найти общее основание и преобразовать уравнение. Тогда поработаем с показателями:

5 2 x — 4 = 49 2 — x

5 2 x — 4 = 7 4 — 2 x

5 2 x — 4 = 1 7 2 x — 4

Закрепить принцип решения показательных уравнений с помощью приведения к одинаковой степени можно на следующем примере:

Приведем части уравнения слева и справа к одному показателю степени. С помощью свойства степенных функций преобразуем правую часть:

2 x — 2 = 1 5 x — 2

Затем следует умножить полученное выражение на 5 x — 2 :

2 x — 2 × 5 x — 2 = 1

Примеры решения показательных уравнений

Найти корни уравнения:

Заметим, что здесь b = 25 > 0 . Таким образом:

Руководствуясь свойствами логарифма, преобразуем выражение:

x = log 5 5 2 = 2 · log 5 5 = 2 · 1 = 2

x 2 x + 1 = x 3 x — 4

Заметим, что данное уравнение равносильно системе:

x = 1 , x ∈ R , x > 0 , x ≠ 1 , 2 x + 1 = 3 x — 4 , x = 0 , 2 x + 1 > 0 , 3 x — 4 > 0

⇒ x = 1 x ∈ 0 ; 1 ∪ 1 ; + ∞ , — x = — 5 , x = 0 , x > — 1 2 , x > 4 3 ⇒

⇒ x = 1 x ∈ 0 ; 1 ∪ 1 ; + ∞ , x = 5 , x = 0 , x > 4 3 ,

Ответ: x 1 = 1 , x 2 = 5

Требуется найти решения уравнения:

2 x — 3 · 4 x = 2 16 x

В первую очередь преобразуем все части равенства так, чтобы основанием было число 2:

Решим приведенное уравнение:

3 x — 3 = 1 2 — 4 x ⇒ 7 x = 7 2 ⇒ x = 1 2 .

Найти корни уравнения:

5 x — 2 · 5 x — 2 = 23

Здесь требуется вынести число 5 в самой маленькой степени, то есть в степени ( х — 2 ). В процессе разделим каждое из слагаемых на этот множитель:

5 x — 2 · 5 x — x — 2 — 2 = 23 ⇒ 5 x — 2 · 5 x — x + 2 — 2 = 23 ⇒ 5 x — 2 · 25 — 2 = 23 ⇒

⇒ 5 x — 2 · 23 = 23 ⇒ 5 x — 2 = 1

x — 2 = log 5 1 ⇒ x — 2 = 0 ⇒ x = 2

С учетом, что 1 = a 0 , уравнение 5 x — 2 = 1 допустимо записать таким образом:

5 x — 2 = 1 ⇒ 5 x — 2 = 5 0 ⇒ x — 2 = 0 ⇒ x = 2

Необходимо решить уравнение:

4 x + 1 — 3 · 2 x = 10

Здесь необходимо привести выражение к единому основанию:

4 x · 4 — 3 · 2 x — 10 = 0 ⇒ 4 · 2 2 x — 3 · 2 x — 10 = 0 ⇒ 4 · 2 x 2 — 3 · 2 x — 10 = 0

Заменим 2 x = t , при этом t больше нуля. Получим:

4 t 2 — 3 t — 10 = 0

Получилось квадратное уравнение, которое можно решить:

D = — 3 2 — 4 · 4 · — 10 = 9 + 160 = 169 = 13 2

t 1 = 3 + 13 2 · 4 = 16 8 = 2

Если выполнить обратную замену, то получится простейшее показательное уравнение 2 x = 2 :

Найти корни уравнения:

3 x + 3 2 — x = 10

3 x + 3 2 · 3 — x = 10 .

Умножим уравнение на 3 x > 0 . Получим:

3 x 2 + 9 = 10 · 3 x ⇒ 3 x 2 — 10 · 3 x + 9 = 0

Заменим 3 x = t , при этом t больше нуля. Получится квадратное уравнение:

t 2 — 10 t + 9 = 0

Согласно теореме Виета, решениями такого уравнения являются:

Выполним обратную замену:

3 x = 9 , 3 x = 1 ⇒ 3 x = 3 2 , 3 x = 3 0

Ответ: x 1 = 2 , x 2 = 0

Вычислить корни уравнения:

В этом случае целесообразно разделить уравнение, то есть все его части, на 3 x + 1 > 0 :

x + 1 = log 2 3 1 ⇒ x + 1 = 0 ⇒ x = — 1

Требуется решить уравнение:

4 x + 6 x = 2 · 9 x

В этом случае следует перенести все слагаемые в левую часть. Затем можно выполнить тождественные преобразования:

2 2 x + 2 · 3 x — 2 · 3 2 x = 0

2 x 2 + 2 x · 3 x — 2 · 3 x 2 = 0 , : 3 2 x > 0

2 3 x 2 + 2 3 x — 2 = 0

Выполним замену 2 3 x = t , где t не равно нулю. В итоге получится квадратное уравнение:

Решения данного уравнения:

t 1 = — 2 0 ∉ , t 2 = 1

Обратная замена даст нам показательное уравнение в простейшем виде:

Показательные уравнения

О чем эта статья:

6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.

Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.