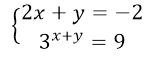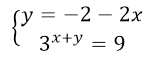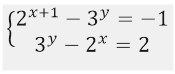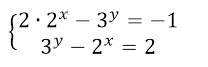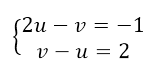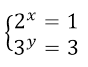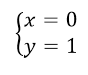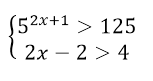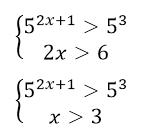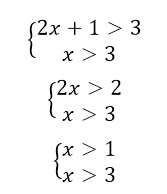Показательные уравнения и системы определения

Показательные уравнения

О чем эта статья:

6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.

Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

Системы показательных уравнений и неравенств

Вы будете перенаправлены на Автор24

Способы решения систем уравнений

Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.

Существуют четыре основных способа решения систем уравнений:

Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$

Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».

Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.

Системы показательных уравнений

Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.

Решение систем показательных уравнений будем рассматривать на примерах.

Решить систему уравнений

Решение.

Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.

Подставим $y$ во второе уравнение:

Ответ: $(-4,6)$.

Решить систему уравнений

Решение.

Данная система равносильна системе

Применим четвертый метод решения уравнений. Пусть $2^x=u\ (u >0)$, а $3^y=v\ (v >0)$, получим:

Решим полученную систему методом сложения. Сложим уравнения:

Тогда из второго уравнения, получим, что

Возвращаясь к замене, получил новую систему показательных уравнений:

Ответ: $(0,1)$.

Готовые работы на аналогичную тему

Системы показательных неравенств

Cистемы неравенств, состоящие из показательных уравнений, называются системой показательных неравенств.

Решение систем показательных неравенств будем рассматривать на примерах.

Решить систему неравенств

Решение:

Данная система неравенств равносильна системе

Для решения первого неравенства вспомним следующую теорему равносильности показательных неравенств:

Теорема 1. Неравенство $a^ >a^ <\varphi (x)>$, где $a >0,a\ne 1$ равносильна совокупности двух систем

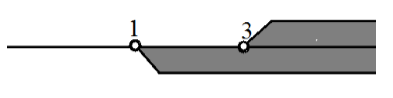
Изобразим оба решения на числовой прямой (рис. 11)

Рисунок 11. Решение примера 3 на числовой прямой

Ответ: $(3,+\infty )$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 03 2021

Показательные уравнения и системы

п.1. Определение показательного уравнения

Например:
1) \(5^=5^3\Leftrightarrow x^2+2=3\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1\)
Мы получили решение: \(x=\pm 1\)
2) \(\left(\frac13\right)^<\sqrt>=\frac<1><\sqrt<3>>\Leftrightarrow \left(\frac13\right)^<\sqrt>=\left(\frac13\right)^<1/2>\Leftrightarrow \sqrt=\frac12\Leftrightarrow \begin x-4=\frac14\\ x-4\geq 0 \end \Leftrightarrow x=4\frac14 \)
Мы получили решение: \(x=4\frac14\)

п.2. Методы решения показательных уравнений

Для решения показательных уравнений применяются следующие методы:
1) переход от уравнения \(a^=a^\) к равносильному уравнению \(f(x)=g(x)\);
2) графический метод;
3) замена переменной.

Первый метод был продемонстрирован выше, второй – показан в примере 3 предыдущего параграфа (§26 данного справочника).
Рассмотрим третий метод.

Решим уравнение \(9^x-6\cdot 3^x-27=0\)
Заметим, что \(9^x=3^<2x>\). Проведём замену переменной \(t=3^x\gt 0\)
Получаем: \(t^2-6t-27\Rightarrow (t+3)(t-9)=0\Rightarrow \left[ \begin t=-3\lt 0 — \text<не подходит>\\ t=9 \end \right. \)
Возвращается к исходной переменной: \(3^x=9\Rightarrow 3^x=3^2\Rightarrow x=2\)
Ответ: 2

При замене переменной в показательном уравнении необходимо помнить, что область значений показательной функции \(t=a^x\gt 9\) — всегда положительна.

п.3. Примеры

в) \(3^x\cdot 4^=0,25\cdot 12^<3-2x>\)
Выражение слева: \(3^x\cdot 4^=3^x\cdot 4^=3^x\cdot 4^x\cdot 4^<-1>=\frac14(3\cdot 4)^x=\frac14\cdot 12^x\)
Подставляем: \(\frac14\cdot 12^x=\frac14\cdot 12^<3-2x>\)
\(12^x=12^<3-2x>\)
\(x=3-2x\)
\(3x=3\)
\(x=1\)
Ответ: 1

e) \(5^x-5\cdot 5^<-x>=4\)
Замена: \(t=5^x\gt 0\)
\(t-\frac5t-4=0\Rightarrow\frac=0\Rightarrow \begin t^2-4t-5=0\\ t\ne 0 \end \Rightarrow \begin (t+1)(t-5)=0\\ t\ne 0 \end\Rightarrow \)
\( \Rightarrow \left[ \begin t=-1\lt 0 — \ \text<не подходит>\\ t=5 \end \right. \)
\(5^x=5\)
\(x=1\)
Ответ: 1

в) \(x\cdot 3^+3\cdot 3^<\sqrt<7-x>>=3^x+x\cdot 3^<\sqrt<7-x>>\)
\(x\cdot 3^-3^x=x\cdot 3^<\sqrt<7-x>>-3\cdot 3^<\sqrt<7-x>>\)
\(3^(x-3)=3^<\sqrt<7-x>>(x-3)\)
\(3^(x-3)-3^<\sqrt<7-x>>(x-3)=0\)
\(\left(3^-3^<\sqrt<7-x>>\right)(x-3)=0\)
\( \left[ \begin 3^-3^<\sqrt<7-x>>=0\\ x-3=0 \end \right. \Rightarrow \left[ \begin 3^=3^<\sqrt<7-x>>\\ x=3 \end \right. \Rightarrow \left[ \begin x-1=\sqrt<7-x>\\ x=3 \end \right. \)
Решаем первое уравнение:
\( \begin (x-1)^2=7-x\\ x-1\geq 0\\ 7-x\geq 0 \end \)
ОДЗ: \( \begin x\geq 1\\ x\leq 7 \end \Rightarrow 1\leq x\leq 7 \)
\(x^2-2x+1=7-x\Rightarrow x^2-x-6\Rightarrow (x+2)(x-3)=0\Rightarrow \left[ \begin x=-2\\ x=3 \end \right. \)
Корень \(x=-2\notin [1;7]\) — не подходит по ОДЗ.
Остается только \(x=3\), который совпадает с корнем из скобки \((x-3)\).
Ответ: 3

г) \(5\cdot 3^<2x>+15\cdot 5^<2x-1>=8\cdot 15^x\) \begin 5\cdot 3^<2x>+\frac<15><5>\cdot 5^<2x>-8\cdot 3^x\cdot 5^x=0\ |:2^<2x>\\ 5+3\cdot\left(\frac53\right)^<2x>-8\cdot\left(\frac53\right)^x=0\\ 3\cdot\left(\frac53\right)^<2x>-8\cdot\left(\frac53\right)^x+5=0 \end Замена: \(t=\left(\frac53\right)^x\gt 0\)
$$ 3t^2-8t+5=0\Rightarrow (3t-5)(t-1)=0\Rightarrow \left[ \begin t=\frac53\\ t=1 \end \right. $$ Оба корня подходят. Возвращаемся к исходной переменной: $$ \left[ \begin \left(\frac53\right)^x=\frac53\\ \left(\frac53\right)^x=1 \end \right. \Rightarrow \left[ \begin x=1\\ x=0 \end \right. $$ Ответ:

д) \((2+\sqrt<3>)^x+(2-\sqrt<3>)^x)=4\)
Заметим, что \((2+\sqrt<3>)\cdot(2-\sqrt<3>)=4-3=1\Rightarrow 2-\sqrt<3>=\frac<1><2+\sqrt<3>>\)
\begin \\ (2+\sqrt<3>)^x+\left(\frac<1><2+\sqrt<3>>\right)^x=4 \end Замена: \(t=(2+\sqrt<3>)^x\)
\begin t+\frac 1t-4=0\Rightarrow \frac=0\Rightarrow \begin t^2-4t+1=0\\ t\ne 0 \end\\ D=4^2-4=12,\ \ t=\frac<4\pm 2\sqrt<3>><2>=2\pm\sqrt <3>\end Оба корня подходят. Возвращаемся к исходной переменной: $$ \left[ \begin (2+\sqrt<3>)^x=2-\sqrt<3>\\ (2+\sqrt<3>)^x=2+\sqrt <3>\end \right. \Rightarrow \left[ \begin x=-1\\ x=1 \end \right. $$ Ответ: \(\left\<\pm 1\right\>\)

e) \(2\sqrt\cdot 4^x+5\cdot 2^+2\sqrt=2^<2x+2>+5\sqrt\cdot 2^x+4\)
ОДЗ: \(x\geq 0\)
\begin 2\sqrt\cdot 4^x-5\sqrt\cdot2^x+2\sqrt=2^<2x+2>-5\cdot 2^+4\\ \sqrt(2\cdot 4^x-5\cdot 2^x+2)=2(2\cdot 4^x-5\cdot 2^x+2)\\ \sqrt(2\cdot 4^x-5\cdot 2^x+2)-2(2\cdot 4^x-5\cdot 2^x+2)=0\\ (\sqrt-2)(2\cdot 4^x-5\cdot 2^x+2)=0\\ \left[ \begin \sqrt-2=0\\ 2\cdot 4^x-5\cdot 2^x+2=0 \end \right. \Rightarrow \left[ \begin x=4\\ \begin 2t^2-5t+2=0\\ t=2^x\gt 0 \end \end \right. \end Решаем квадратное уравнение: \begin 2t^2-5t+2=0\Rightarrow (2t-1)(t-2)=0\Rightarrow \left[ \begin t=\frac12\\ t=2 \end \right. \\ \left[ \begin 2^x=\frac12\\ 2^x=2 \end \right. \Rightarrow \left[ \begin x=-1\\ x=1 \end \right. \end \(x=-1\) — не подходит по ОДЗ (в исходном уравнении есть \(\sqrt\)).
Остается \(x=1\). И ещё есть \(x=4\) из скобки (\(\sqrt-2\)).
Ответ:

Пример 3. Решите систему:
a) \( \begin 2^x\cdot 4^y=64\\ 3^x\cdot 81^y=3^ <10>\end \) \begin \begin 2^x\cdot 2^<2y>=2^6\\ 3^x\cdot 3^<4y>=3^ <10>\end \Rightarrow \begin 2^=2^6\\ 3^=3^ <10>\end \Rightarrow \begin x+2y=6\\ x+4y=10 \end \overset<(-)> <\Rightarrow>\begin 2y=10-6\\ x=6-2y \end \Rightarrow \begin x=2\\ y=2 \end \end Ответ: (2;2)

в) \( \begin 3^x-2^<2y>=77\\ 3^-2^y=7 \end \)
Замена: \( \begin a=3^\gt 0\\ b=2^y\gt 0 \end \) \begin \\ \begin a^2-b^2=77\\ a-b=7 \end \Rightarrow \begin (a-b)(a+b)=77\\ a-b=7 \end \Rightarrow \begin a+b=11\\ a-b=7 \end \overset<(\pm)> <\Rightarrow>\begin 2a=11+7\\ 2b=11-7 \end \Rightarrow \begin a=9\\ b=2 \end \end Возвращаемся к исходным переменным: $$ \begin 3^=9\\ 2^y=2 \end \Rightarrow \begin \frac x2=2\\ y=1 \end \Rightarrow \begin x=4\\ y=1 \end $$ Ответ: (4;1)

г) \( \begin 2^x+2^y=12\\ x+y=5 \end \)
\( \begin 2^x+2^<5-x>=12\\ y=5-x \end \)
Решаем первое уравнение: \(2^x+\frac<2^5><2^x>=12\)
\(t=2^x\gt 0\) \begin \\ t+\frac<32>-12=0\Rightarrow \frac=0 \Rightarrow \begin t^2-12t+32=0\\ t\ne 0 \end \\ t^2-12t+32=0\Rightarrow (t-4)(t-8)=0\Rightarrow \left[ \begin t=4\\ t=8 \end \right. \\ \left[ \begin 2^x=4\\ 2^x=8 \end \right. \Rightarrow \left[ \begin x=2\\ x=3 \end \right. \end Получаем две пары решений: \( \left[ \begin \begin x=2\\ y=5-x=3 \end\\ \begin x=3\\ y=5-x=2 \end \end \right. \)
Ответ:

д*) \( \begin 4^<-x>+4^<-y>=\frac<33><64>\\ 2^=8\sqrt <2>\end \)
\begin \\ \begin \left(\frac12\right)^<2x>+\left(\frac12\right)^<2y>=\frac<33><64>\\ \frac<1><2^>=\frac<1><4\sqrt<2>> \end \Rightarrow \begin \left(\frac12\right)^<2x>+\left(\frac12\right)^<2y>=\frac<33><64>\\ \left(\frac12\right)^x\left(\frac12\right)^y=\frac<1><8\sqrt<2>> \end \end Замена: \( \begin a=\left(\frac12\right)^\gt 0\\ b=\left(\frac12\right)^\gt 0 \end \)
\begin \\ \begin a^2+b^2=\frac<33><64>\\ ab=\frac<1><8\sqrt<2>> \end \Rightarrow \begin a^2+\left(\frac<1><8\sqrt<2>a>\right)^2=\frac<33><64>\\ b=\frac<1><8\sqrt<2>a> \end \Rightarrow \begin a^2+\frac<1><128a^2>=\frac<33><64>\\ b=\frac<1><8\sqrt<2>a> \end \end Решаем биквадратное уравнение: \begin a^2+\frac<1><128a^2>=\frac<33><64>\Rightarrow \frac<128a^4-66a^2+1><128a^2>=0\Rightarrow \begin 128a^4-66a^2+1=0\\ a\ne 0 \end \\ 128a^4-66a^2+1=0\Rightarrow (64a^2-1)(2a^2-1)=0\Rightarrow \left[ \begin a^2=\frac<1><64>\\ a^2=\frac12 \end \right. \end По определению замены берем положительные корни: \( \left[ \begin a=\frac18\\ a=\frac<1><\sqrt<2>> \end \right. \)
Получаем две пары решений: \( \left[ \begin \begin a=\frac18\\ b=\frac<1><8\sqrt<2>a>=\frac<1><\sqrt<2>> \end \\ \begin a=\frac<1><\sqrt<2>>\\ b=\frac<1><8\sqrt<2>a>=\frac18 \end \end \right. \)
Возвращаемся к исходным переменным:
\( \left[ \begin \begin \left(\frac12\right)^x=\frac18\\ \left(\frac12\right)^y=\frac<1><\sqrt<2>> \end \\ \begin \left(\frac12\right)^x=\frac<1><\sqrt<2>>\\ \left(\frac12\right)^y=\frac18 \end \end \right. \Rightarrow \left[ \begin \begin \left(\frac12\right)^x=\left(\frac12\right)^3\\ \left(\frac12\right)^y=\left(\frac12\right)^ <0,5>\end \\ \begin \left(\frac12\right)^x=\left(\frac12\right)^<0,5>\\ \left(\frac12\right)^y=\left(\frac12\right)^3 \end \end \right. \Rightarrow \left[ \begin \begin x=3\\ y=0,5 \end \\ \begin x=0,5\\ y=3 \end \end \right. \)
Ответ: