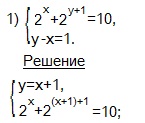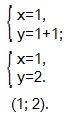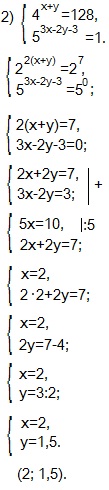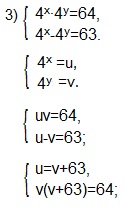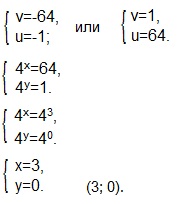Показательные уравнения и системы уравнений 10 класс

11.3.6. Решение систем показательных уравнений

Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений.

Решить системы уравнений:

Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.

Решаем (2) -ое уравнение полученной системы:

2 х +2 x +2 =10, применяем формулу: a x + y =a x ∙a y .

2 x +2 x ∙2 2 =10, вынесем общий множитель 2 х за скобки:

2 х (1+2 2 )=10 или 2 х ∙5=10, отсюда 2 х =2.

2 х =2 1 , отсюда х=1. Возвращаемся к системе уравнений.

Ответ: (1; 2).

Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5.

Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.

Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.

Находим х=2 и это значение подставляем вместо х во второе уравнение системы.

Находим у.

Ответ: (2; 1,5).

Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.

Решаем (2) -ое уравнение системы.

v 2 +63v-64=0. Подберем корни по теореме Виета, зная, что: v₁+v₂=-63; v₁∙v₂=-64.

Получаем: v₁=-64, v₂=1. Возвращаемся к системе, находим u.

Так как значения показательной функции всегда положительны, то уравнения 4 x = -1 и 4 y = -64 решений не имеют.

Представляем 64 и 1 в виде степеней с основанием 4.

Приравниваем показатели степеней и находим х и у.

Показательные уравнения и системы

п.1. Определение показательного уравнения

Например:
1) \(5^=5^3\Leftrightarrow x^2+2=3\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1\)
Мы получили решение: \(x=\pm 1\)
2) \(\left(\frac13\right)^<\sqrt>=\frac<1><\sqrt<3>>\Leftrightarrow \left(\frac13\right)^<\sqrt>=\left(\frac13\right)^<1/2>\Leftrightarrow \sqrt=\frac12\Leftrightarrow \begin x-4=\frac14\\ x-4\geq 0 \end \Leftrightarrow x=4\frac14 \)
Мы получили решение: \(x=4\frac14\)

п.2. Методы решения показательных уравнений

Для решения показательных уравнений применяются следующие методы:
1) переход от уравнения \(a^=a^\) к равносильному уравнению \(f(x)=g(x)\);
2) графический метод;
3) замена переменной.

Первый метод был продемонстрирован выше, второй – показан в примере 3 предыдущего параграфа (§26 данного справочника).
Рассмотрим третий метод.

Решим уравнение \(9^x-6\cdot 3^x-27=0\)
Заметим, что \(9^x=3^<2x>\). Проведём замену переменной \(t=3^x\gt 0\)
Получаем: \(t^2-6t-27\Rightarrow (t+3)(t-9)=0\Rightarrow \left[ \begin t=-3\lt 0 — \text<не подходит>\\ t=9 \end \right. \)
Возвращается к исходной переменной: \(3^x=9\Rightarrow 3^x=3^2\Rightarrow x=2\)
Ответ: 2

При замене переменной в показательном уравнении необходимо помнить, что область значений показательной функции \(t=a^x\gt 9\) — всегда положительна.

п.3. Примеры

в) \(3^x\cdot 4^=0,25\cdot 12^<3-2x>\)
Выражение слева: \(3^x\cdot 4^=3^x\cdot 4^=3^x\cdot 4^x\cdot 4^<-1>=\frac14(3\cdot 4)^x=\frac14\cdot 12^x\)
Подставляем: \(\frac14\cdot 12^x=\frac14\cdot 12^<3-2x>\)
\(12^x=12^<3-2x>\)
\(x=3-2x\)
\(3x=3\)
\(x=1\)
Ответ: 1

e) \(5^x-5\cdot 5^<-x>=4\)
Замена: \(t=5^x\gt 0\)
\(t-\frac5t-4=0\Rightarrow\frac=0\Rightarrow \begin t^2-4t-5=0\\ t\ne 0 \end \Rightarrow \begin (t+1)(t-5)=0\\ t\ne 0 \end\Rightarrow \)
\( \Rightarrow \left[ \begin t=-1\lt 0 — \ \text<не подходит>\\ t=5 \end \right. \)
\(5^x=5\)
\(x=1\)
Ответ: 1

в) \(x\cdot 3^+3\cdot 3^<\sqrt<7-x>>=3^x+x\cdot 3^<\sqrt<7-x>>\)
\(x\cdot 3^-3^x=x\cdot 3^<\sqrt<7-x>>-3\cdot 3^<\sqrt<7-x>>\)
\(3^(x-3)=3^<\sqrt<7-x>>(x-3)\)
\(3^(x-3)-3^<\sqrt<7-x>>(x-3)=0\)
\(\left(3^-3^<\sqrt<7-x>>\right)(x-3)=0\)
\( \left[ \begin 3^-3^<\sqrt<7-x>>=0\\ x-3=0 \end \right. \Rightarrow \left[ \begin 3^=3^<\sqrt<7-x>>\\ x=3 \end \right. \Rightarrow \left[ \begin x-1=\sqrt<7-x>\\ x=3 \end \right. \)
Решаем первое уравнение:
\( \begin (x-1)^2=7-x\\ x-1\geq 0\\ 7-x\geq 0 \end \)
ОДЗ: \( \begin x\geq 1\\ x\leq 7 \end \Rightarrow 1\leq x\leq 7 \)
\(x^2-2x+1=7-x\Rightarrow x^2-x-6\Rightarrow (x+2)(x-3)=0\Rightarrow \left[ \begin x=-2\\ x=3 \end \right. \)
Корень \(x=-2\notin [1;7]\) — не подходит по ОДЗ.
Остается только \(x=3\), который совпадает с корнем из скобки \((x-3)\).
Ответ: 3

г) \(5\cdot 3^<2x>+15\cdot 5^<2x-1>=8\cdot 15^x\) \begin 5\cdot 3^<2x>+\frac<15><5>\cdot 5^<2x>-8\cdot 3^x\cdot 5^x=0\ |:2^<2x>\\ 5+3\cdot\left(\frac53\right)^<2x>-8\cdot\left(\frac53\right)^x=0\\ 3\cdot\left(\frac53\right)^<2x>-8\cdot\left(\frac53\right)^x+5=0 \end Замена: \(t=\left(\frac53\right)^x\gt 0\)
$$ 3t^2-8t+5=0\Rightarrow (3t-5)(t-1)=0\Rightarrow \left[ \begin t=\frac53\\ t=1 \end \right. $$ Оба корня подходят. Возвращаемся к исходной переменной: $$ \left[ \begin \left(\frac53\right)^x=\frac53\\ \left(\frac53\right)^x=1 \end \right. \Rightarrow \left[ \begin x=1\\ x=0 \end \right. $$ Ответ:

д) \((2+\sqrt<3>)^x+(2-\sqrt<3>)^x)=4\)
Заметим, что \((2+\sqrt<3>)\cdot(2-\sqrt<3>)=4-3=1\Rightarrow 2-\sqrt<3>=\frac<1><2+\sqrt<3>>\)
\begin \\ (2+\sqrt<3>)^x+\left(\frac<1><2+\sqrt<3>>\right)^x=4 \end Замена: \(t=(2+\sqrt<3>)^x\)
\begin t+\frac 1t-4=0\Rightarrow \frac=0\Rightarrow \begin t^2-4t+1=0\\ t\ne 0 \end\\ D=4^2-4=12,\ \ t=\frac<4\pm 2\sqrt<3>><2>=2\pm\sqrt <3>\end Оба корня подходят. Возвращаемся к исходной переменной: $$ \left[ \begin (2+\sqrt<3>)^x=2-\sqrt<3>\\ (2+\sqrt<3>)^x=2+\sqrt <3>\end \right. \Rightarrow \left[ \begin x=-1\\ x=1 \end \right. $$ Ответ: \(\left\<\pm 1\right\>\)

e) \(2\sqrt\cdot 4^x+5\cdot 2^+2\sqrt=2^<2x+2>+5\sqrt\cdot 2^x+4\)
ОДЗ: \(x\geq 0\)
\begin 2\sqrt\cdot 4^x-5\sqrt\cdot2^x+2\sqrt=2^<2x+2>-5\cdot 2^+4\\ \sqrt(2\cdot 4^x-5\cdot 2^x+2)=2(2\cdot 4^x-5\cdot 2^x+2)\\ \sqrt(2\cdot 4^x-5\cdot 2^x+2)-2(2\cdot 4^x-5\cdot 2^x+2)=0\\ (\sqrt-2)(2\cdot 4^x-5\cdot 2^x+2)=0\\ \left[ \begin \sqrt-2=0\\ 2\cdot 4^x-5\cdot 2^x+2=0 \end \right. \Rightarrow \left[ \begin x=4\\ \begin 2t^2-5t+2=0\\ t=2^x\gt 0 \end \end \right. \end Решаем квадратное уравнение: \begin 2t^2-5t+2=0\Rightarrow (2t-1)(t-2)=0\Rightarrow \left[ \begin t=\frac12\\ t=2 \end \right. \\ \left[ \begin 2^x=\frac12\\ 2^x=2 \end \right. \Rightarrow \left[ \begin x=-1\\ x=1 \end \right. \end \(x=-1\) — не подходит по ОДЗ (в исходном уравнении есть \(\sqrt\)).
Остается \(x=1\). И ещё есть \(x=4\) из скобки (\(\sqrt-2\)).
Ответ:

Пример 3. Решите систему:
a) \( \begin 2^x\cdot 4^y=64\\ 3^x\cdot 81^y=3^ <10>\end \) \begin \begin 2^x\cdot 2^<2y>=2^6\\ 3^x\cdot 3^<4y>=3^ <10>\end \Rightarrow \begin 2^=2^6\\ 3^=3^ <10>\end \Rightarrow \begin x+2y=6\\ x+4y=10 \end \overset<(-)> <\Rightarrow>\begin 2y=10-6\\ x=6-2y \end \Rightarrow \begin x=2\\ y=2 \end \end Ответ: (2;2)

в) \( \begin 3^x-2^<2y>=77\\ 3^-2^y=7 \end \)
Замена: \( \begin a=3^\gt 0\\ b=2^y\gt 0 \end \) \begin \\ \begin a^2-b^2=77\\ a-b=7 \end \Rightarrow \begin (a-b)(a+b)=77\\ a-b=7 \end \Rightarrow \begin a+b=11\\ a-b=7 \end \overset<(\pm)> <\Rightarrow>\begin 2a=11+7\\ 2b=11-7 \end \Rightarrow \begin a=9\\ b=2 \end \end Возвращаемся к исходным переменным: $$ \begin 3^=9\\ 2^y=2 \end \Rightarrow \begin \frac x2=2\\ y=1 \end \Rightarrow \begin x=4\\ y=1 \end $$ Ответ: (4;1)

г) \( \begin 2^x+2^y=12\\ x+y=5 \end \)
\( \begin 2^x+2^<5-x>=12\\ y=5-x \end \)
Решаем первое уравнение: \(2^x+\frac<2^5><2^x>=12\)
\(t=2^x\gt 0\) \begin \\ t+\frac<32>-12=0\Rightarrow \frac=0 \Rightarrow \begin t^2-12t+32=0\\ t\ne 0 \end \\ t^2-12t+32=0\Rightarrow (t-4)(t-8)=0\Rightarrow \left[ \begin t=4\\ t=8 \end \right. \\ \left[ \begin 2^x=4\\ 2^x=8 \end \right. \Rightarrow \left[ \begin x=2\\ x=3 \end \right. \end Получаем две пары решений: \( \left[ \begin \begin x=2\\ y=5-x=3 \end\\ \begin x=3\\ y=5-x=2 \end \end \right. \)
Ответ:

д*) \( \begin 4^<-x>+4^<-y>=\frac<33><64>\\ 2^=8\sqrt <2>\end \)
\begin \\ \begin \left(\frac12\right)^<2x>+\left(\frac12\right)^<2y>=\frac<33><64>\\ \frac<1><2^>=\frac<1><4\sqrt<2>> \end \Rightarrow \begin \left(\frac12\right)^<2x>+\left(\frac12\right)^<2y>=\frac<33><64>\\ \left(\frac12\right)^x\left(\frac12\right)^y=\frac<1><8\sqrt<2>> \end \end Замена: \( \begin a=\left(\frac12\right)^\gt 0\\ b=\left(\frac12\right)^\gt 0 \end \)
\begin \\ \begin a^2+b^2=\frac<33><64>\\ ab=\frac<1><8\sqrt<2>> \end \Rightarrow \begin a^2+\left(\frac<1><8\sqrt<2>a>\right)^2=\frac<33><64>\\ b=\frac<1><8\sqrt<2>a> \end \Rightarrow \begin a^2+\frac<1><128a^2>=\frac<33><64>\\ b=\frac<1><8\sqrt<2>a> \end \end Решаем биквадратное уравнение: \begin a^2+\frac<1><128a^2>=\frac<33><64>\Rightarrow \frac<128a^4-66a^2+1><128a^2>=0\Rightarrow \begin 128a^4-66a^2+1=0\\ a\ne 0 \end \\ 128a^4-66a^2+1=0\Rightarrow (64a^2-1)(2a^2-1)=0\Rightarrow \left[ \begin a^2=\frac<1><64>\\ a^2=\frac12 \end \right. \end По определению замены берем положительные корни: \( \left[ \begin a=\frac18\\ a=\frac<1><\sqrt<2>> \end \right. \)
Получаем две пары решений: \( \left[ \begin \begin a=\frac18\\ b=\frac<1><8\sqrt<2>a>=\frac<1><\sqrt<2>> \end \\ \begin a=\frac<1><\sqrt<2>>\\ b=\frac<1><8\sqrt<2>a>=\frac18 \end \end \right. \)
Возвращаемся к исходным переменным:
\( \left[ \begin \begin \left(\frac12\right)^x=\frac18\\ \left(\frac12\right)^y=\frac<1><\sqrt<2>> \end \\ \begin \left(\frac12\right)^x=\frac<1><\sqrt<2>>\\ \left(\frac12\right)^y=\frac18 \end \end \right. \Rightarrow \left[ \begin \begin \left(\frac12\right)^x=\left(\frac12\right)^3\\ \left(\frac12\right)^y=\left(\frac12\right)^ <0,5>\end \\ \begin \left(\frac12\right)^x=\left(\frac12\right)^<0,5>\\ \left(\frac12\right)^y=\left(\frac12\right)^3 \end \end \right. \Rightarrow \left[ \begin \begin x=3\\ y=0,5 \end \\ \begin x=0,5\\ y=3 \end \end \right. \)
Ответ:

Презентация к уроку алгебры в 10 классе «Системы показательных уравнений и неравенств» (учебник Алимова и др.)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Системы показательных уравнений и неравенств

у 1 =3
х 1 =−7
х 2 =1
у 2 =−1

Пусть 𝟐 х =𝒖, 𝟑 𝒚 =𝒗, тогда
нет решения

Проверочная работа.
Вариант 1.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 956 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 685 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 569 552 материала в базе

Материал подходит для УМК

«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.

§ 14. Системы показательных уравнений и неравенств

Другие материалы

• 01.10.2021
• 578
• 154

• 01.10.2021
• 1871
• 596

• 01.10.2021
• 2816
• 604

• 01.10.2021
• 1009
• 185

• 30.09.2021
• 117
• 0

• 30.09.2021
• 116
• 0

• 30.09.2021
• 836
• 7

• 30.09.2021
• 673
• 24

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.10.2021 1011
• PPTX 761.2 кбайт
• 284 скачивания
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Артемьева Оксана Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 3 месяца
• Подписчики: 1
• Всего просмотров: 19930
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.