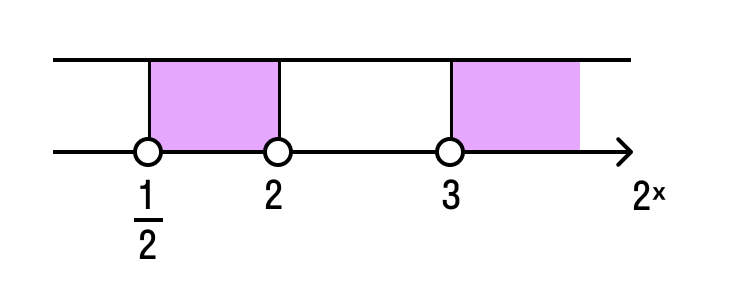
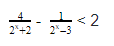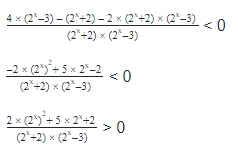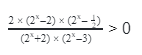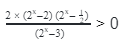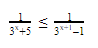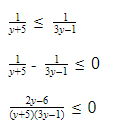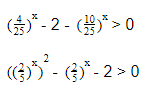ЕГЭ Профиль №15. Показательные неравенства
15 заданием профильного ЕГЭ по математике является неравенство. Одним, из наиболее часто встречаемых неравенств, которое может оказаться в 15 задание, является показательное неравенство. Большая часть показательных неравенств предлагаемых на реальных экзаменах решается с помощью замен, методом интервалов или разложением на множители. Прежде чем решать показательные неравенства необходимо знать свойства показательной функции и уметь решать показательные уравнения (см. задание 13 профильного ЕГЭ « Показательные уравнения »). В данном разделе представлены показательные неравенства (всего 109) разбитые на два уровня сложности. Уровень А — это простейшие показательные неравенства, которые являются подготовительными для решения реальных показательных неравенств предлагаемых на ЕГЭ по профильной математике. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.
Решение показательных неравенств.
Рассматриваются типовые показательные неравенства и неравенства, соответствующие заданию 14 профильного уровня ЕГЭ по математике. Все неравенства даны с решениями и комментариями, поэтому будут полезны и при текущем изучении или повторении этой темы.
Если возникают вопросы — обращайтесь через форму для письма, рисунок конверта кликабелен.
Узнайте, как можно поддержать сайт и помочь его развитию.
Основные положения и примеры решения простейших показательных неравенств.
Показательные неравенства содержат переменную в показателе степени. В случае, если вам встретилось неравенство, в котором переменная не только в показателе, но и в основании степени, попробуйте применить метод рационализации, о котором несколько слов в конце статьи. Если же неизвестная величина только в основании степени, а показатели фиксированы, то это неравенство относится к рациональным и содержит не показательные, а степенные функции.
Чтобы решать показательные неравенства нужно вспомнить, что мы знаем о показательной функции.
Область определения показательной функции D = R, то есть всё множество действительных чисел. Иначе записывают \(x\in(-\infty; +\infty)\). Область значений функции \(E = (0; +\infty)\), т.е. результат может принимать только положительные значения.
Функция монотонна: одному значению аргумента соответствует только одно значение функции.
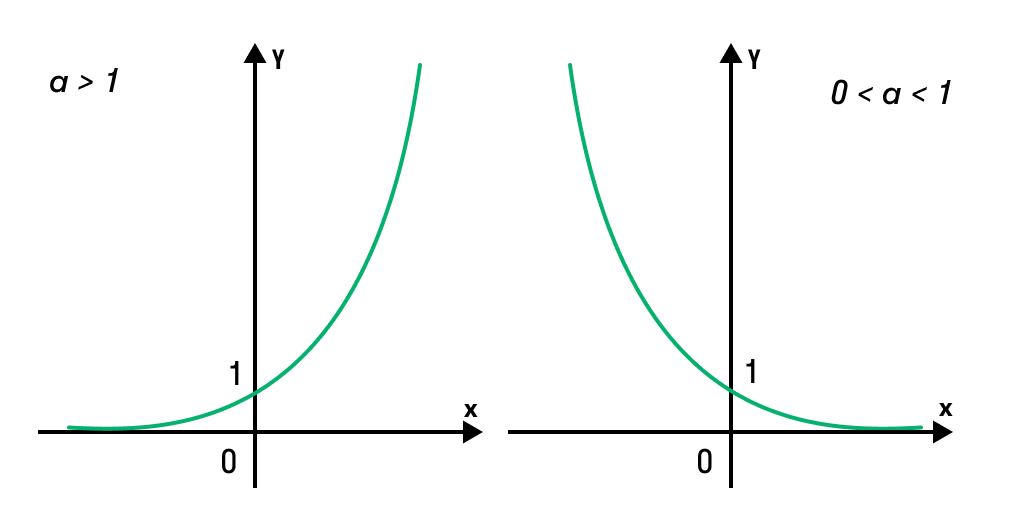
При a > 1 функция возрастающая,
Поэтому для решения простейших показательных неравенств достаточно свести обе части неравенства к степени с одинаковым основанием (выравнять основания) и затем сравнить показатели степени. Т.е. как бы сравнивать функцию с самой собой при разных значениях её аргумента. При этом, если основание степени больше единицы, то знак неравенства для показателей будет таким же, как знак исходного неравенства, что характерно для возрастающих функций – большему значению аргумента соответствует большее значение функции. Если основание степени меньше единицы, то знак неравенства для показателей будет обратным по отношению к знаку исходного неравенства, что характерно для убывающих функций – большему значению аргумента соответствует меньшее значение функции.
Пример 1.
Решить неравенство \[\left(\frac<1><3>\right)^
Решение.
Представим одну девятую как одну третью в квадрате, тогда \[\left(\frac<1><3>\right)^
Решение.
На первый взгляд числа 3 и 5 таковы, что выражения не могут быть сведены к одному основанию в какой-либо степени. На этот случай у нас определена обратная к показательной логарифмическая функция. Мы говорим, что обе части неравенства нужно прологарифмировать по одному основанию. Однако, на мой взгляд, именно для решения неравенств лучше всего использовать следующее свойство логарифма, вытекающее из его определения \(b = a^<\log_ab>\). Здесь основания степени и логарифма совпадают, поэтому при вычислении логарифма как бы «сокращаются», значит «восстановить» можно любые допустимые значения, нужные для решения конкретного неравенства. Этим приёмом мы и будем пользоваться в дальнейшем, чтобы разбираться со знаком неравенства по той же схеме, что и в предыдущих двух примерах.
Итак, представим правую часть неравенства следующим образом \(5 = 3^<\log_35>,\) тогда \[ 3^
Ответ: \(x \in [-5 + \log_3<5>;\; +\infty). \)
Итак, при решении простейших неравенств следует выравнять основания степеней, а затем их отбросить и перейти к сравнению показателей. При этом очень важно следить за отношением основания степени к единице. Если \(a > 1\) при переходе к сранению показателей знак неравенства сохраняется, если \(a x 2 − 8x 7
Решение.
Заметим, что 0,2 = \(\dfrac<1><5>\) и уравняем основания левой и правой части. \[\left(\frac<1><5>\right)^
Ответ: x ∈ (−∞;1) ∪ (7;+∞).
Введение вспомогательной переменной
Решение.
Преобразуем левую часть, используя свойства степеней. \[3^4\cdot3^ <-3x>— 35\cdot\frac<1^<2 - 3x>><3^<2 - 3x>> + 6 \ge 0; \\ \frac<3^4><3^<3x>> — 35\cdot\frac<1><3^2\cdot3^<- 3x>> + 6 \ge 0; \\ \frac<3^4><3^<3x>> — 35\cdot\frac<3^<3x>> <3^2>+ 6 \ge 0. \]
В последнем неравенстве неизвестная величина встречается дважды и только в показателе степени тройки, причем оба раза в одинаковой форме, поэтому можно продолжить решение методом введения вспомогательной переменной.
Пусть \(y = 3^<3x>\). Причём по определению показательной функции мы должны рассматривать только положительные значения y. Тогда неравенство принимает вид \[\frac<3^4>
Ответ: \(x \in (-\infty; \;\dfrac<1><3>\log_3\dfrac<27><5>) \).
Замечание: При желании этот ответ можно преобразовать, используя формулу для логарифма дроби. \[\frac<1><3>\log_3\frac<27> <5>= \frac<1><3>(\log_327 — \log_35) = \frac<1><3>(3 — \log_35) = 1 — \frac<1><3>\log_35. \]
Разложение на множители
Решение.
Здесь в правой и левой частях неравенства разные основания и привести выражение к одному основанию, пользуясь только свойствами степени не получится, потому что свойства относятся к операциям умножения, деления и возведения в степень, а мы имеем с обеих сторон суммы показательных функций. В этом случае надо стараться разложить выражения на множители. Здесь это можно будет сделать вынесением общего множителя за скобки, а вообще для решения подобных неравенств очень рекомендую повторить различные способы разложения на множители, особенно формулы сокращенного умножения. \[ 3^
О методе рационализации.
Метод рационализации для показательных неравенств сводится к следующему:
неравенство вида \[(h(x))^<\large
Очевидно, что в случае числового основания степени это решение не является более простым и более понятным, чем решение предыдущих примеров. Метод рационализации существенно сокращает объём рассуждений и выкладок, когда в основании степени также как и в её показателе находятся неизвестные переменные величины. И хотя такие неравенства относятся к более сложным типам, чем те, которые бывают на ЕГЭ даже профильного уровня, рассмотрим пример.
Решение.
Обратите внимание – для решения показательных неравенств методом рационализации тоже нужно выравнивать основания степеней или, как в этом примере, иметь их одинаковыми по условию задачи.
Заменяем неравенство на равносильную систему \[\begin
\[\left(\frac
Решив, получим корни \(\dfrac<1-\sqrt<5>> <2>\approx -0,62\) и \(\dfrac<1+\sqrt<5>> <2>\approx 1,62\).
Обратите внимание – дробь с неизвестными в знаменателе можно сокращать только после того, как записали ОДЗ. Мы ОДЗ не записывали, поэтому сокращать не будем. Тот факт, что на 0 делить нельзя, отметим непосредственно на числовой оси.
Общее решение системы
Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
Показательные неравенства
О чем эта статья:
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a f(x) > a g(x) , a f(x) g(x) .
Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.
Для изучения этой темы стоит повторить:
И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.
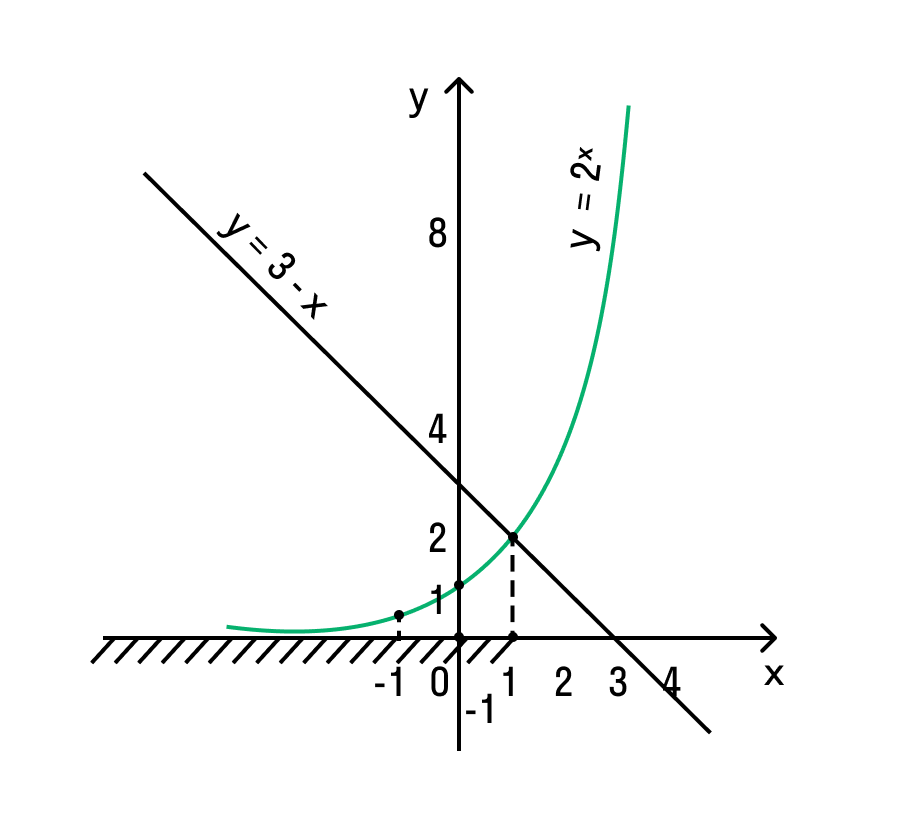
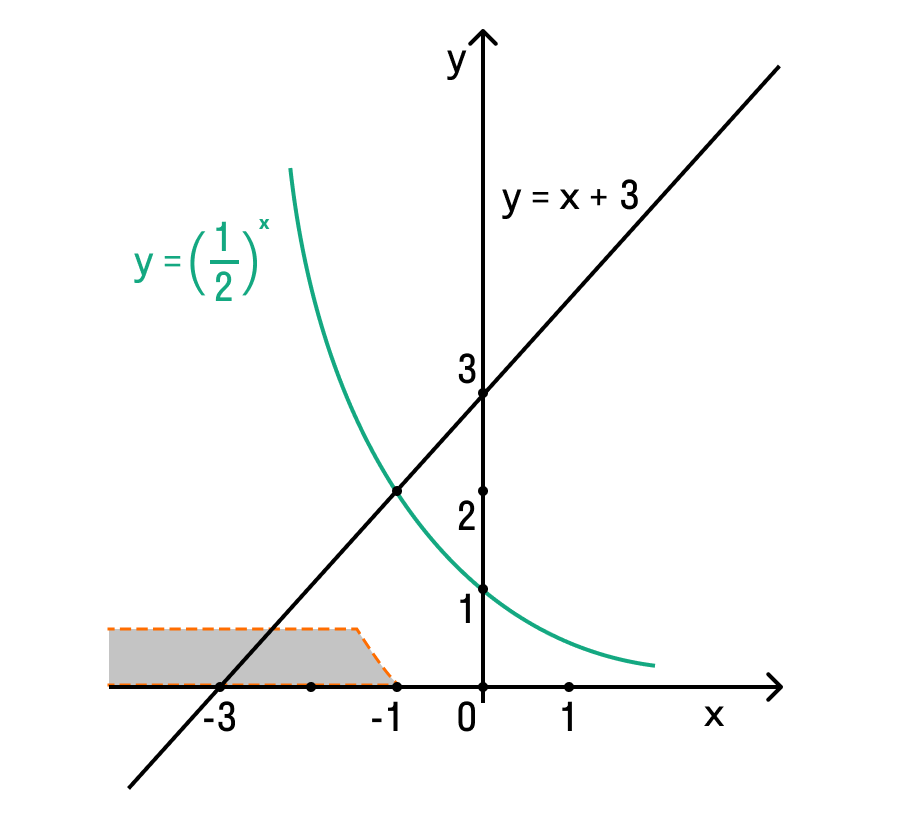
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x , где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2 -2 = 4, 2 -4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство a x > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
- a f(x) > a g(x) f(x) > g (x), когда функция возрастает, т. е. а > 1;
- a f(x) > a g(x) f(x)
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости.
Допустим, у нас есть простейшее показательное неравенство:
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
Проверим, верно ли в таком случае х > 2.
0,5 3 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х