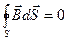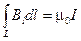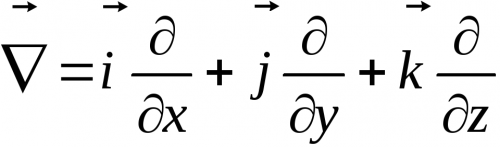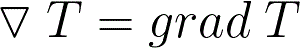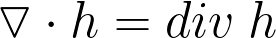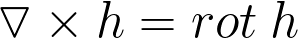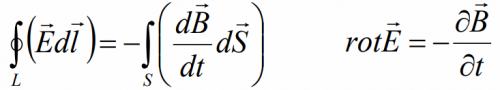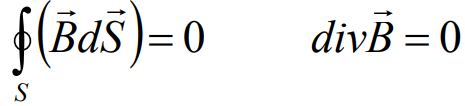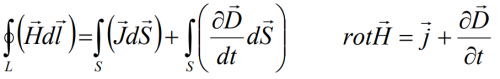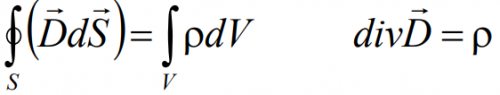Введение в теорию электромагнитного поля (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

13. ВВЕДЕНИЕ В ТЕОРИЮ

13.1. полная система уравнений

13.1.1. Основные величины,

характеризующие электромагнитное поле

Электромагнитное поле – это особый вид материи, который является носителем энергии и оказывает силовое воздействие на заряженные частицы и тела. Оно характеризуется способностью распространяться даже в пустоте (электромагнитные волны) и непрерывностью распределения в пространстве, но вместе с тем проявляет дискретную структуру (фотоны). Для упрощения анализа у единого электромагнитного поля принято выделять две составляющие, которые можно обнаружить по отдельности при выборе соответствующей системы отсчета.

Электрическое поле выявляется по силовому воздействию на неподвижные заряженные тела и частицы, магнитное поле – по силовому воздействию на неподвижные проводники с токами или на движущиеся заряженные тела и частицы. В курсе физики даются определения основных величин, характеризующих эти составляющие, описываются электрические и магнитные свойства различных сред, в которых поля существуют. Краткое изложение соответствующего раздела физики дано в разделе 1 первой части пособия [6].

В табл. 13.1 приведены обозначения и единицы измерения основных величин, характеризующих электромагнитное поле (ЭМП) в каждой точке пространства в любой момент времени.

Вектор напряженности электрического поля

Вектор напряженности магнитного поля

Вектор электрического смещения

Вектор магнитной индукции

Тл ()

Вектор плотности электрического тока

Объемная плотность электрического заряда

Поверхностная плотность заряда

Скалярный магнитный потенциал

Векторный магнитный потенциал

Плотность энергии электрического поля

Плотность энергии магнитного поля

Электрическое и магнитное поля неразрывно связаны между собой. Эта взаимосвязь математически описывается уравнениями электродинамики, которые выведены Максвеллом.

13.1.2. Первое уравнение Максвелла

Электрический ток возбуждает в окружающем пространстве электрическое поле. Согласно закону полного тока

. (13.1а)

Выберем небольшой контур интегрирования Dl, охватывающий поверхность Ds, к элементам которой вектор плотности тока d нормален. Затем найдем предел отношения левой и правой частей уравнения (13.1а) к площади этой поверхности, уменьшая площадь до нуля:

В результате получится первое уравнение Максвелла:

. (13.1б)

Физический смысл уравнения: в точках пространства, где существует электрический ток, магнитное поле имеет вихревой характер.

13.1.3. Второе уравнение Максвелла

Другая сторона взаимосвязи двух составляющих поля отражена в законе электромагнитной индукции: в замкнутом контуре Dl переменное магнитное поле наводит ЭДС

. (13.2а)

В правой части уравнения учитывается магнитный поток , пронизывающий площадку S, ограниченную контуром l. Если повторить уже знакомую операцию – отыскать пределы отношения обеих частей уравнения (13,2а) к площади S при S ® 0, то, очевидно, получится выражение

. (13.2б)

Это и есть второе уравнение Максвелла. Его физический смысл: электрическое поле имеет вихревой характер в тех точках пространства, где существует переменное магнитное поле.

13.1.4. Постулат Максвелла и теорема Гаусса

Интегральная форма этого уравнения устанавливает связь потока вектора электрического смещения с зарядами, которые создают электрическое поле:

. (13.3а)

Здесь – свободный заряд, который произвольным образом распределен с плотностью r по объему V , ограниченному поверхностью S. Выберем небольшую замкнутую поверхность Ds, ограничивающую объем DV с распределенным внутри зарядом Dq, и найдем пределы, к которым стремятся отношения левой и правой частей уравнения (13.3а) к величине этого объема, когда сам объем стремится к нулю:

В результате получим дифференциальную форму постулата Максвелла:

. (13.3б)

Смысл этого уравнения в том, что линии вектора электрического смещения начинаются и кончаются на зарядах.

Из положительных зарядов линии выходят , в отрицательные заряды – входят . Если в рассматриваемой точке заряд отсутствует, то .

Из интегральной формы теоремы Гаусса

, (13.3в)

которая применима лишь в случае однородной изотропной среды с абсолютной диэлектрической проницаемостью , с помощью знакомых преобразований нетрудно получить дифференциальную форму:

(13.3г)

В формулах (13.3а–13.3г) в правой части учитывается лишь свободный заряд. Если электрическое поле возникает за счет изменения магнитного, то в правой части окажется нуль. Линии напряженности такого поля в однородной изотропной среде непрерывны.

13.1.5. Принцип непрерывности магнитного поля

Магнитный поток сквозь замкнутую поверхность равен нулю (интегральная форма):

. (13.4а)

Дифференциальную форму принципа непрерывности (13.4б) легко получить из уравнения (13.4а), если с ним проделать те же операции, что и с формулой (13.3а):

. (13.4б)

Это значит, что линии вектора магнитной индукции непрерывны.

13.1.6. Соотношения, характеризующие свойства среды

Электрический ток может иметь различную природу. Его плотность можно представить в виде трех составляющих:

.

Первое слагаемое характеризует ток проводимости, который представляет собой упорядоченное движение электронов или ионов в проводящей среде под действием электрического поля и связан с напряженностью электрического поля законом Ома в дифференциальной форме: = gЕ. Второе слагаемое определяет плотность тока смещения и связано со скоростью изменения вектора смещения электрического поля: . Этот ток существует в диэлектриках. Третье слагаемое учитывает перемещение заряженных частиц в вакууме или газообразной среде: . Здесь r и v – усредненные значения объемной плотности зарядов и скорости их движения. Разумеется, в каждой точке пространства может существовать лишь один из видов тока, а в виде суммы они представлены для общности записи:

. (13.5)

Связь векторов, характеризующих электрическое поле в изотропном диэлектрике, выражается формулой

(13.6)

Подобное же соотношение связывает и векторы, характеризующие магнитное поле в изотропной среде:

(13.7)

В последних двух формулах абсолютные диэлектрическая и магнитная проницаемости могут быть выражены через относительные проницаемости (индекс r) и с использованием фундаментальных констант:

Ф/м – электрическая постоянная,

Гн/м – магнитная постоянная.

13.1.7. Полная система уравнений ЭМП и оператор Гамильтона

Полная система уравнений (инвариантных по отношению к преобразованию системы координат), описывающих электромагнитное поле в каждой точке пространства в любой момент времени, приведена в табл. 13.2.

Уравнения электромагнитного поля

в интегральной форме

в дифференциальной форме

(13.1а)

(13.1б)

(13.2а)

(13.2б)

(13.3а)

(13.3б)

(13.4а)

(13.4б)

, (13.5) (13.6) (13.7)

К этим уравнениям можно добавить и формулу для определения плотности энергии электромагнитного поля:

. (13.8)

Уравнения (13.1б–13.4б) – это уравнения в частных производных, которые просто и удобно записываются с помощью дифференциального оператора Гамильтона «набла», имеющего в декартовой системе координат следующий вид:

. (13.9)

Формально это вектор, обладающий дифференциальными способностями. Скалярное произведение оператора «набла» на некоторый вектор равно дивергенции последнего. Если же вычислить векторное произведение оператора на тот же вектор, то получится ротор этого вектора. Поэтому вышеупомянутые уравнения можно переписать в виде:

(13.10)

Расчет электромагнитного поля предполагает решение полной системы уравнений при заданных граничных и начальных условиях. Рассмотрим наиболее простые и распространенные методы расчета на примере статических (стационарных) полей.

13.2. Электростатическое поле

Это поле неподвижных и неизменных во времени электрических зарядов. Вообще говоря, такие поля в чистом виде не встречаются, поскольку под действием кулоновских сил заряды способны перемещаться. Напомним, что по закону Кулона два точечных заряда и , находящиеся на расстоянии d в среде с диэлектрической проницаемостью , взаимодействуют друг с другом с силой

.

Одноименные заряды отталкиваются, разноименные – притягиваются. Но даже если силы притяжения и отталкивания в некоторой системе зарядов уравновешены, то это равновесие неустойчиво и нарушается при малейшем внешнем воздействии. Тем не менее, во многих практически важных случаях, как показывает опыт, квазистатические поля можно с высокой степенью точности рассчитывать теми же методами, что и статические.

13.2.1. Уравнение Лапласа–Пуассона

Если нет электрического тока (d = 0) и движущихся намагниченных тел, то отсутствует и переменное магнитное поле. Поэтому формулы (13.2а) и (13.2б) примут вид:

, (13.11а)

. (13.11б)

Последнее выражение означает, что электростатическое поле – безвихревое и, стало быть, потенциальное. Иными словами, существует такая функция координат j (x, y, z), которая удовлетворяет условию

. (13.12)

Подстановка (13.12) в (13.11б) приводит к тождеству: rot grad j º 0.

Функция j называется потенциалом. Ее физический смысл как меры энергии электрического поля пояснялся разделе 1 [6]. В расчетах электростатического поля важно то обстоятельство, что с введением этой величины решение системы трех уравнений сводится к решению одного. Действительно, подстановки – сначала (13.12) в (13.6), а затем результата в (13.3б) дают для однородной и изотропной среды:

Отсюда следует уравнение Пуассона

(13.13)

После вычисления скалярного произведения оператора «набла» на самого себя получается дифференциальный оператор «лапласиан», который в декартовой системе координат имеет вид:

(13.14)

При отсутствии в данной точке пространства свободных зарядов получим уравнение Лапласа (частный случай уравнения Пуассона, описывающий, строго говоря, именно электростатическое поле):

(13.15)

13.2.2. Теорема единственности и ее следствия

Уравнения (13.13) и (13.15) как уравнения в частных производных имеют бесконечно большое количество решений. Выбрать из них то, которое относится именно к конкретной задаче, позволяет теорема единственности решения уравнения Лапласа–Пуассона: если существует функция, удовлетворяющая уравнению Лапласа–Пуассона и граничным условиям данного поля, то это решение единственное. Теорема для случая заряженных тел легко доказывается «от противного» с использованием энергетических соотношений [2].

Под граничными условиями понимают, во-первых, соотношения между составляющими векторов поля на поверхности раздела двух сред с различными свойствами. В электростатике это либо два диэлектрика, либо проводник и диэлектрик. Такие условия иногда называют однородными, имея в виду то, что они справедливы для любой задачи. Во-вторых, это либо известное распределение потенциала или составляющих векторов поля на границе области, либо известные значения потенциалов и зарядов системы тел. Эти условия можно назвать неоднородными, относящимися лишь к конкретной задаче. (Сравните роль тех и других в расчете поля с ролью независимых и зависимых начальных условий при анализе переходных процессов).

Из теоремы единственности следуют два положения, имеющих важное практическое значение.

Следствие 1. Электростатическое поле в некоторой области, ограниченной эквипотенциальными поверхностями, не изменится, если эти поверхности сделать проводящими с соответствующими потенциалами.

Следствие 2. Электростатическое поле по одну сторону некоторой граничной поверхности не изменится, если по другую сторону этой поверхности изменить параметры среды и распределение зарядов таким образом, чтобы граничные условия на этой поверхности полностью сохранились (принцип «зарядов-изображений»).

13.2.3. Граничные условия на поверхности раздела двух сред

с различными диэлектрическими проницаемостями

Выделим на поверхности раздела двух диэлектриков точку и рассмотрим электростатическое поле вблизи нее. Окружим эту точку некоторой замкнутой поверхностью, например, цилиндром, высота которого гораздо меньше диаметра оснований. На рис. 13.1,а контур abcda – это след цилиндрической поверхности в плоскости чертежа, которая проходит через ось цилиндра. Вычислим поток вектора электрического смещения D сквозь эту поверхность и воспользуемся постулатом Максвелла (13.3а). Учитывая соотношение размеров цилиндра, потоком сквозь боковую поверхность можно пренебречь, подсчитав лишь поток сквозь поверхности оснований :

.

Здесь – заряд, находящийся внутри цилиндра, фактически распределенный по поверхности раздела с плотностью s. Будем полагать и поверхности оснований столь малыми, что в их пределах векторы и не меняются. В результате интегрирования скалярных произведений векторов с учетом их расположения по отношению к нормали получим: . Тогда

(13.16а)

Итак, в точке, лежащей на поверхности раздела двух диэлектриков, нормальные составляющие вектора электрического смещения отличаются на величину поверхностной плотности свободного заряда в этой точке.

Если же эти заряды отсутствуют, то нормальные составляющие вектора электрического смещения на границе равны. Именно этому случаю соответствует расположение векторов на рис. 13.1,а:

(13.16б)

Теперь окружим ту же точку прямоугольным контуром abcda в плоскости чертежа (рис. 13.1,б) и воспользуемся формулой (13.11а), сохранив соотношение .

Получим. Если считать и отрезки ab и cd столь малыми, что в их пределах векторы и не меняются, то интегралы от скалярных произведений с учетом расположения векторов по отношению к нормали перейдут в равенство: . Отсюда

(13.17)

В точке, лежащей на поверхности раздела двух диэлектриков, касательные составляющие вектора напряженности электрического поля равны. Это условие также означает, что при переходе через поверхность раздела двух диэлектриков потенциал изменяется плавно, без скачков даже при наличии свободных зарядов на этой поверхности. Если же эти заряды отсутствуют, то из формул (13.16б) и (13.17) с учетом соотношения (13.6) следует еще одно условие:

. (13.18)

13.2.4. Граничные условия на поверхности раздела

проводника и диэлектрика

Если проводящее тело находится во внешнем электростатическом поле, то вследствие явления электростатической индукции внутри тела произойдет разделение зарядов. Отрицательные заряды переместятся на поверхность, обращенную в сторону более высокого потенциала, положительные – на противоположную. Если же само тело заряжено, то заряды одного знака под действием сил отталкивания также расположатся на поверхности проводника. В любом случае внутри проводника не может быть свободных зарядов (r = 0) и электростатическое поле отсутствует, так что

(13.19)

Это означает, что все точки проводящего тела, включая его поверхность, имеют один и тот же потенциал (j = const). Следовательно, на поверхности проводника отсутствуют касательные составляющие напряженности электрического поля

(13.20)

а есть только нормальные составляющие. То же самое можно сказать и про составляющие вектора электрического смещения. А если по отношению к точке на поверхности проводника (рис. 13.1,в) повторить рассуждения, которые были сделаны по поводу рис. 13.1,а, то получится условие

(13.21)

13.2.5. Плоскопараллельное и плоскомеридианное поля

Расчет поля существенно упрощается, если все величины, характеризующие поле, зависят только от двух координат той или иной системы.

Поле называется плоскопараллельным, если его потенциал не зависит от одной из координат декартовой системы. Иными словами, картина поля, т. е. совокупность эквипотенциальных линий и линий напряженности поля, одинакова во всех плоскостях, перпендикулярных этой оси координат. Эквипотенциальные линии – это следы поверхностей равного потенциала в плоскости чертежа. Линии напряженности электрического поля – это линии, в каждой точке которых вектор напряженности электрического поля направлен по касательной к ним.

Градиент потенциала равен отношению приращения потенциала к приращению линейной координаты в направлении, в котором это приращение имеет наибольшее значение, т. е.

.

Очевидно, такое направление соответствует нормали к поверхности равного потенциала. Поэтому линии напряженности поля всегда перпендикулярны эквипотенциальным линиям.

Поле называется плоскомеридианным, если его потенциал не зависит от азимутальной координаты цилиндрической системы. Картина такого поля одинакова во всех плоскостях, проходящих через ось вращения системы.

Для того, чтобы картина давала количественное представление об интенсивности поля, потенциалы соседних эквипотенциалей должны отличаться на одинаковую величину. В свою очередь должен быть одинаков и поток вектора напряженности поля в каждой трубке поля (на картине поля это область между соседними линиями напряженности).

Самыми простыми для расчета оказываются поля уединенных тел или системы нескольких тел, обладающих определенной симметрией, причем известны или потенциалы, или полные заряды этих тел. Познакомимся с наиболее распространенными методами расчета именно таких задач на конкретных примерах. При этом для упрощения анализа ограничимся рассмотрением областей с однородной изотропной средой.

13.2.6. Расчет полей в областях с простой геометрией

13.2.6.1. Применение теоремы Гаусса в интегральной форме

Использование соотношения (13.3б) целесообразно в тех случаях, когда легко вычисляется входящий в эту формулу интеграл. Для этого следует выбрать такую поверхность интегрирования, чтобы вектор напряженности поля был либо нормален к одной ее части, либо был направлен по касательной к другой части. Такой подход, в частности, использовался при анализе поля плоского конденсатора (пример 1.1 раздела 1 [6]). Приведем еще один важный пример.

Полная система уравнений Максвелла и их физический смысл

В основе максвелловской теории классической электродинамики лежат следующие четыре уравнения

1) 3)

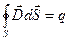
2) 4) .

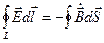
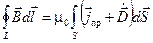
Повторим физический смысл этих уравнений.

Уравнение 1. Теорема о потоке вектора напряженности электрического поля. Источником электростатического поля являются электрические заряды.

Уравнение 2. Теорема о циркуляции вихревого электрического поля. Переменное магнитное поле является источником вихревого электрического поля. По существу это уравнение выражает фарадеевский закон электромагнитной индукции.

Уравнение 3.Теорема о потоке вектора магнитной индукции. В природе не существуют магнитные заряды.

Уравнение 4. Теорема о циркуляции магнитного поля. Магнитные поля могут возбуждаться либо электрическими токами, либо переменными электрическими полями.

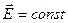
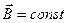
Для стационарных полей, когда и , уравнения Максвелла записываются в следующем виде

1) 3)

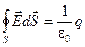
2) 4)

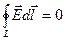
В уравнении 2 подчёркивается потенциальный характер электростатических полей.

Уравнение (4) означает, что источником стационарного магнитного поля являются только токи проводимости.

Величины, входящие в уравнения Максвелла, не являются независимыми. Между ними существуют следующие связи.

,

,

.

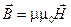
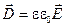
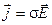
Здесь: m, e — магнитная и диэлектрическая проницаемость вещества;

— вектор плотности тока проводимости;

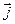
s —удельная электропроводность среды.

Последние уравнения называются материальными, поскольку величины m, e и s входят в уравнения Максвелла как материальные константы.

Лекция 13 «Электромагнитные волны»

1. Волновой процесс. Уравнение плоской волны. Волновое уравнение.

2. Плоская электромагнитная волна. Свойства электромагнитных волн.

3. Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.

4. Примеры вычисления плотности потока энергии.

4.1. Плотность потока энергии в плоской электромагнитной волне.

4.2. Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.

В этой лекции нам предстоит показать, что уравнения классической электродинамики Максвелла, которые мы сформулировали на прошлой лекции, с неизбежностью приводят к идее электромагнитной волны.

Начнем с ответа на вопрос: что такое волна?

Дата добавления: 2015-08-08 ; просмотров: 723 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды: