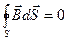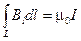Полная система уравнений максвелла справедлива при наличии

Полная система уравнений Максвелла и их физический смысл

В основе максвелловской теории классической электродинамики лежат следующие четыре уравнения

1) 3)

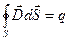
2) 4) .

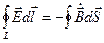
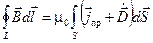
Повторим физический смысл этих уравнений.

Уравнение 1. Теорема о потоке вектора напряженности электрического поля. Источником электростатического поля являются электрические заряды.

Уравнение 2. Теорема о циркуляции вихревого электрического поля. Переменное магнитное поле является источником вихревого электрического поля. По существу это уравнение выражает фарадеевский закон электромагнитной индукции.

Уравнение 3.Теорема о потоке вектора магнитной индукции. В природе не существуют магнитные заряды.

Уравнение 4. Теорема о циркуляции магнитного поля. Магнитные поля могут возбуждаться либо электрическими токами, либо переменными электрическими полями.

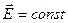
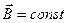
Для стационарных полей, когда и , уравнения Максвелла записываются в следующем виде

1) 3)

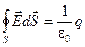
2) 4)

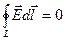
В уравнении 2 подчёркивается потенциальный характер электростатических полей.

Уравнение (4) означает, что источником стационарного магнитного поля являются только токи проводимости.

Величины, входящие в уравнения Максвелла, не являются независимыми. Между ними существуют следующие связи.

,

,

.

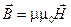
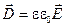
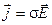
Здесь: m, e — магнитная и диэлектрическая проницаемость вещества;

— вектор плотности тока проводимости;

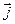
s —удельная электропроводность среды.

Последние уравнения называются материальными, поскольку величины m, e и s входят в уравнения Максвелла как материальные константы.

Лекция 13 «Электромагнитные волны»

1. Волновой процесс. Уравнение плоской волны. Волновое уравнение.

2. Плоская электромагнитная волна. Свойства электромагнитных волн.

3. Энергия электромагнитных волн. Плотность потока энергии. Вектор Пойнтинга.

4. Примеры вычисления плотности потока энергии.

4.1. Плотность потока энергии в плоской электромагнитной волне.

4.2. Плотность потока энергии электромагнитного поля в цепи постоянного тока. Выделение джоулева тепла в проводнике.

В этой лекции нам предстоит показать, что уравнения классической электродинамики Максвелла, которые мы сформулировали на прошлой лекции, с неизбежностью приводят к идее электромагнитной волны.

Начнем с ответа на вопрос: что такое волна?

Дата добавления: 2015-08-08 ; просмотров: 739 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнения Максвелла

Вы будете перенаправлены на Автор24

Значение уравнений Максвелла

Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.

Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.

Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.

Система уравнений Максвелла

Систему уравнений Максвелла составляют:

Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow\ и\ \overrightarrow$), а во вторую пару — вспомогательные ($\overrightarrow\ и\ \overrightarrow$).

Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:

Готовые работы на аналогичную тему

В скалярном виде уравнение (2) запишем как:

Третье уравнение из системы Максвелла в скалярном виде:

Четвертое уравнение в скалярной форме примет следующий вид:

Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:

Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.

Физический смысл уравнений Максвелла

Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow$) и токи смещения ($\frac<\partial \overrightarrow><\partial t>$).

Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.

Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.

Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.

Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).

Уравнения поля линейны и учитывают принцип суперпозиции.

Границы применимости уравнений Максвелла

Система уравнений Максвелла ограничена следующими условиями:

Материальные тела должны быть неподвижны в поле.

Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.

В поле не должно находиться постоянных магнитов и ферромагнитных тел.

Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.

Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.

Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.

Решение:

В качестве основания для решения задачи используем из системы Максвелла уравнение:

Проведем операцию дивергирования в обеих частях выражения (1.1):

Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:

Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:

В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:

Что позволяет нам записать уравнение (1.4) в виде:

Что дает нам закон сохранения заряда, который записан в виде:

Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:

тогда если области замкнуты и изолированы получаем:

Что требовалось доказать.

Задание: Покажите, что уравнения $rot\overrightarrow=-\frac<\partial \overrightarrow><\partial t>$ и $div\overrightarrow=0$ , входящие в систему Максвелла не противоречат друг другу.

Решение:

За основу решения примем уравнение:

Возьмём дивергенцию от обеих частей уравнения:

В соответствии с теоремой равенстве нулю дивергенции ротора имеем:

Соответственно, получаем, что

Выражение $div\overrightarrow=const$ не противоречит тому, что $div\overrightarrow=0$.

Мы получили, что уравнения $rot\overrightarrow=-\frac<\partial \overrightarrow><\partial t>$ и $div\overrightarrow=0$ совместны, что требовалось показать.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 03 2021

МА́КСВЕЛЛА УРАВНЕ́НИЯ

МА́КСВЕЛЛА УРАВНЕ́НИЯ, ос­но­во­по­ла­гаю­щие урав­не­ния клас­сич. мак­ро­ско­пич. элек­тро­ди­на­ми­ки, опи­сы­ваю­щие за­ко­но­мер­но­сти элек­тро­маг­нит­ных яв­ле­ний в сплош­ной сре­де или ва­куу­ме (в пре­неб­ре­же­нии кван­то­вы­ми яв­ле­ния­ми). Тео­рия элек­тро­маг­нит­но­го поля бы­ла раз­ра­бо­та­на Дж. К. Мак­свел­лом в 1856–73. В М. у. обоб­ще­ны ра­нее ус­та­нов­лен­ные опыт­ные за­ко­ны элек­трич. и маг­нит­ных яв­ле­ний, и эти за­ко­ны объ­е­ди­не­ны с кон­цеп­ци­ей М. Фа­ра­дея об элек­тро­маг­нит­ном по­ле, обес­пе­чи­ваю­щем взаи­мо­дей­ст­вие ме­ж­ду уда­лён­ны­ми за­ря­жен­ны­ми те­ла­ми (т. н. тео­рия близ­ко­дей­ст­вия). В ори­ги­наль­ном из­ло­же­нии Мак­свел­ла бы­ло соз­на­тель­но при­ве­де­но из­бы­точ­ное чис­ло урав­не­ний; при этом Мак­свелл ис­поль­зо­вал ма­те­ма­тич. ап­па­рат ква­тер­нио­нов Га­миль­то­на. Совр. фор­му М. у. с ис­поль­зо­ва­ни­ем век­тор­но­го ис­чис­ле­ния при­да­ли Г. Р. Герц и О. Хе­ви­сайд . М. у. свя­зы­ва­ют век­тор­ные по­ле­вые ве­ли­чи­ны (яв­ляю­щие­ся функ­ция­ми ко­ор­ди­нат и вре­ме­ни) с ис­точ­ни­ка­ми элек­тро­маг­нит­но­го по­ля – рас­пре­де­лён­ны­ми в про­стран­ст­ве и из­ме­няю­щи­ми­ся во вре­ме­ни элек­трич. за­ря­да­ми и то­ка­ми. М. у. име­ют вид (диф­фе­рен­ци­аль­ная фор­ма М. у. в СИ): $$\textrm\,\boldsymbol E=-\frac<\partial \boldsymbol B><\partial t>,\quad \textrm\,\boldsymbol H=\boldsymbol j+\frac<\partial \boldsymbol D><\partial t>,\\ \textrm