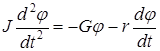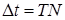II. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГООБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
З.Г.Морозова
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
к лабораторной работе по дисциплине «Физика»
Рекомендовано к изданию методическим советом
электротехнического факультета ФГБОУ ВПО «ВятГУ»
кандидат педагогических наук, доцент, кафедры «Прикладной математики и информатики» ФГБОУ ВПО «ВятГУ» Хохлова М.В.
| Изучение затухающих колебаний крутильного маятника и колебательного разряда конденсатора: учебно-методическое пособие к лабораторной работе по дисциплине «Физика» для студентов всех технических профилей подготовки, всех форм обучения / З.Г. Морозова. – Киров: Изд–во ВятГУ, 2015. –20с. |
© Морозова З.Г., 2015
© ФГБОУ ВПО «ВятГУ», 2015
Морозова Зоя Григорьевна.
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ КРУТИЛЬНОГО МАЯТНИКА И
КОЛЕБАТЕЛЬНОГО РАЗРЯДА КОНДЕНСАТОРА
к лабораторной работе по дисциплине «Физика»
Подписано в печать . Печать цифровая. Бумага для офисной техники.
Усл. печ. л. . Тираж 103 экз. Заказ .
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Вятский государственный университет»
610000, Киров, ул. Московская, 36, тел.: (8332) 64-23-56, http://vyatsu.ru
ЦЕЛЬ РАБОТЫ: изучить особенности возникающих в механических и электрических колебательных системах затухающих колебаний; измерение характеристик различных затухающих колебаний; выяснение влияния на них параметров колебательных систем.
I. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Затухающие колебания – это колебания, амплитуда которых из-за потерь энергии колебательной системы с течением времени уменьшается. Простейшим механизмом уменьшения амплитуды колебания является её превращение в теплоту вследствие; трения в механических колебательных системах, а также омических потерь и излучение электромагнитной энергии в электрических колебательных системах.
Уравнение затухающих колебаний определяется свойствами колебательных систем. Обычно рассматриваются линейные системы — идеализированные реальные системы, в которых параметры, определяющие их физические свойства, в ходе процесса не меняются. Линейными, например, являются математический маятник при малых амплитудах колебаний; колебательный контур, если его индуктивность и ёмкость не зависят ни от тока в контуре, ни от подаваемого напряжения.
Независимо от природы колебательного процесса дифференциальное уравнение затухающих колебаний линейной системы задается в виде:

где 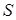


Решением уравнения (1) является функция:
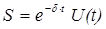
После нахождения первой и второй производных выражения (2) и подстановки их в уравнение (1) получим:

Решение уравнения (3) зависит от знака коэффициента при 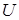
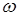

где 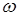

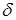
С учетом выражения (4) уравнение (3)запишется:

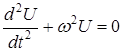
решением этого уравнения является функция вида

Следовательно, с учётом уравнений (2) и (5) решение уравнения (1) запишется:

где 
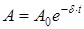
где 
График зависимости S(t) при затухающих колебаниях (6) приведена на рис. 1.
Затухающие колебания не являются периодическими, так как максимальное значение колеблющейся величины S1, достигнутое в некоторый момент времени t1 в последующем (при t > t1) никогда не повторится. Однако, при затухающих колебаниях величина S обращается в нуль, а также достигает максимальных значений через равные промежутки времени:

Величину Т обычно называют периодом (условным периодом) затухающих колебаний.
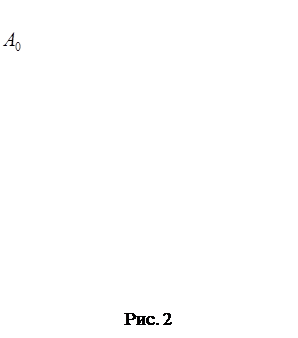

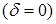
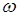
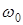
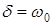

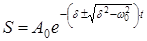
причём очевидно, что 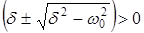
График апериодического движения приведен на рис. 2.
Время в течение, которого амплитуда затухающего колебания (7) уменьшается в 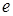
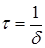


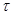
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний используется логарифмический декремент затухания.
Логарифмическим декрементом затухания называется безразмерная величина 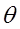
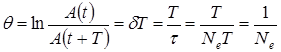
где 



Для характеристики изменения энергии колебательной системы используют понятие добротности 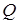
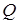
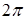




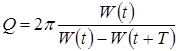
Так как 
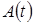
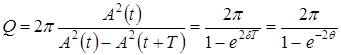
При условии малого затухания 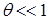
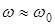

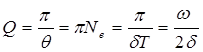
где Т= 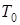




Полученные общие выводы можем применить для конкретных линейных систем.
В данной работе изучаются механические затухающие колебания на примере крутильного маятника и электромагнитные затухающие колебания на примере электрического колебательного контура.
II. КРУТИЛЬНЫЕ КОЛЕБАНИЯ
В данной лабораторной работе механические колебания изучаются на примере крутильного маятника, представляющего собой массивное тело цилиндрической формы, подвешенное на упругой нити. Схема маятника изображена на рис. 3. Для торможения движения маятника используется трансформаторное масло, налитое в стакан С.



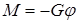
где 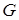
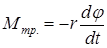
где 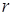

Если 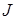

Введя обозначения 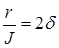
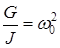

Уравнение (13) совпадает с уравнением (1) и, следовательно, крутильные колебания маятника будут происходить по закону затухающих колебаний (6).
Если за некоторое время 
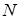
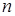
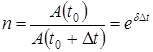
где 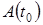

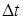
По определению время N колебаний равно
Логарифмический декремент затухания (6)c учетом (14) равен:
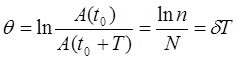
Добротность маятника 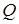

Гармонические колебания
О чем эта статья:
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
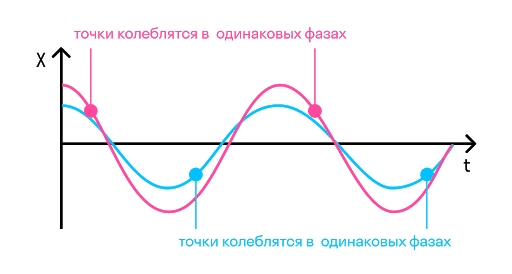
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
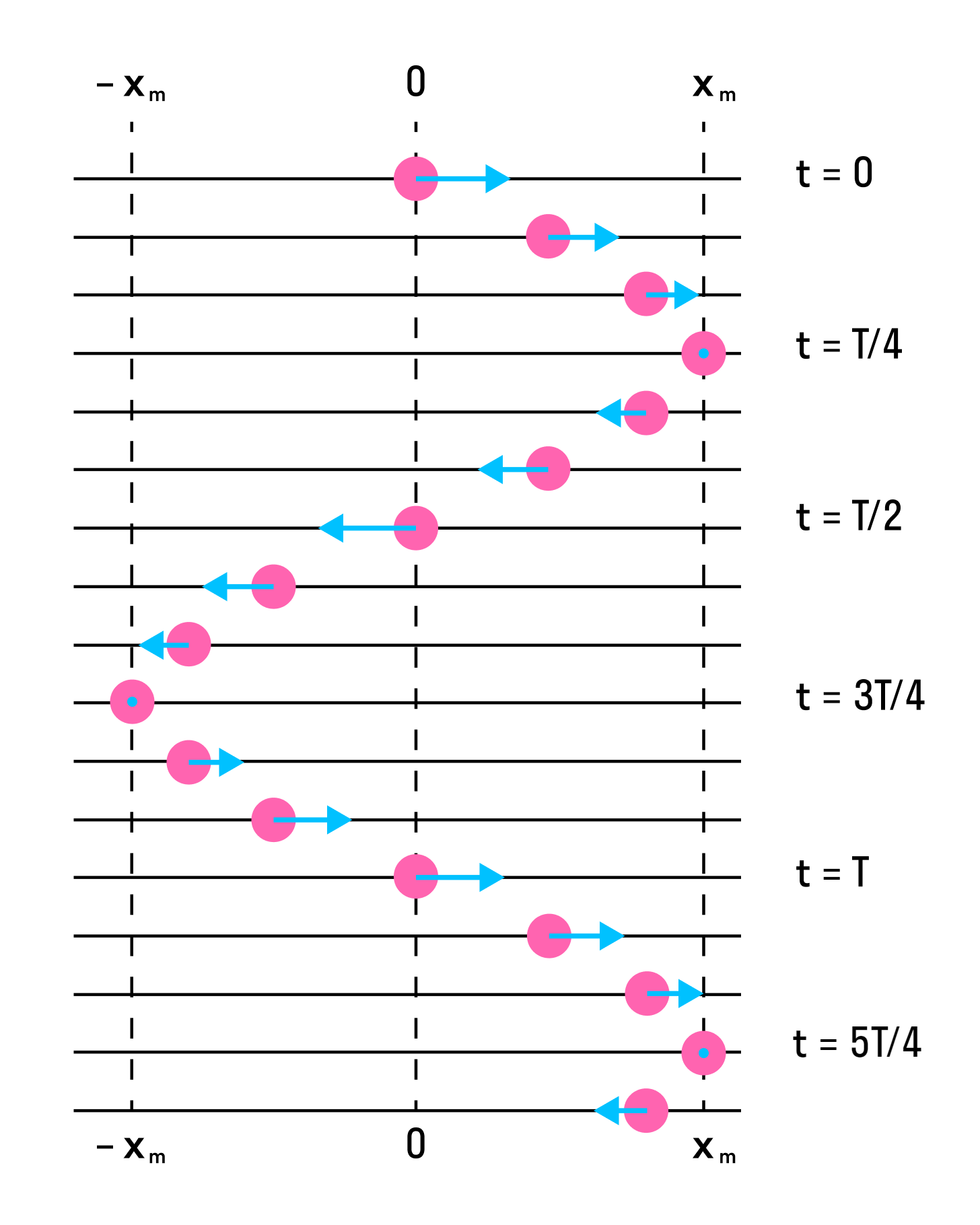
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
l — длина нити [м]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
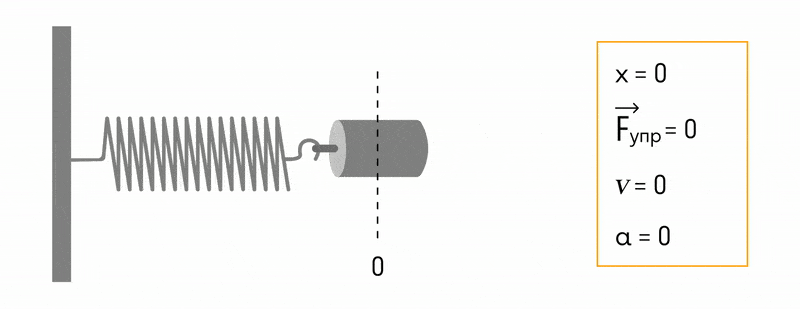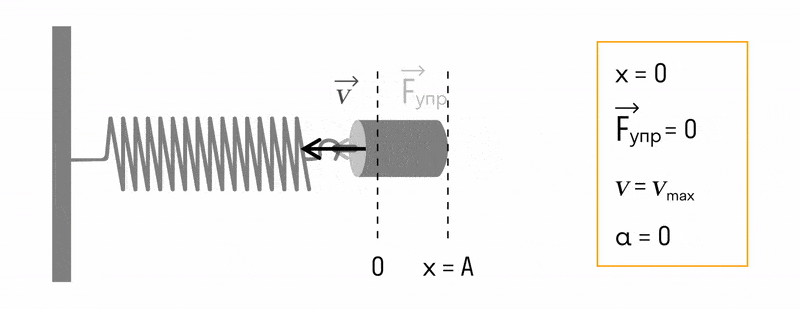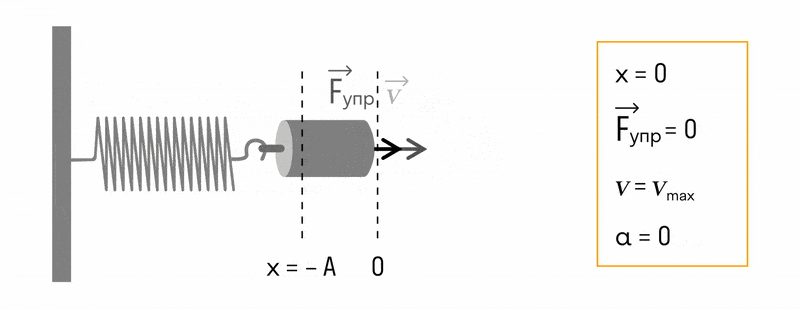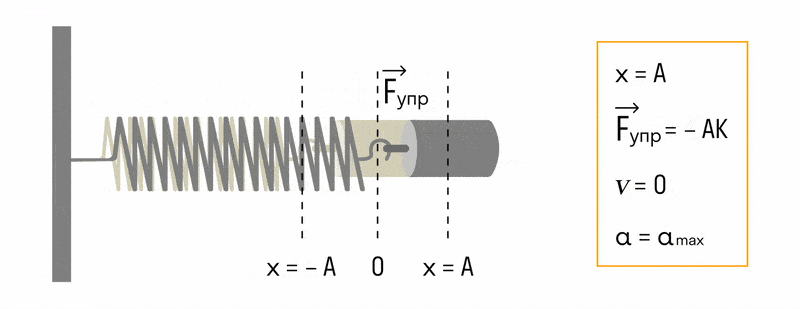
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
m — масса маятника [кг]
k — жесткость пружины [Н/м]
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
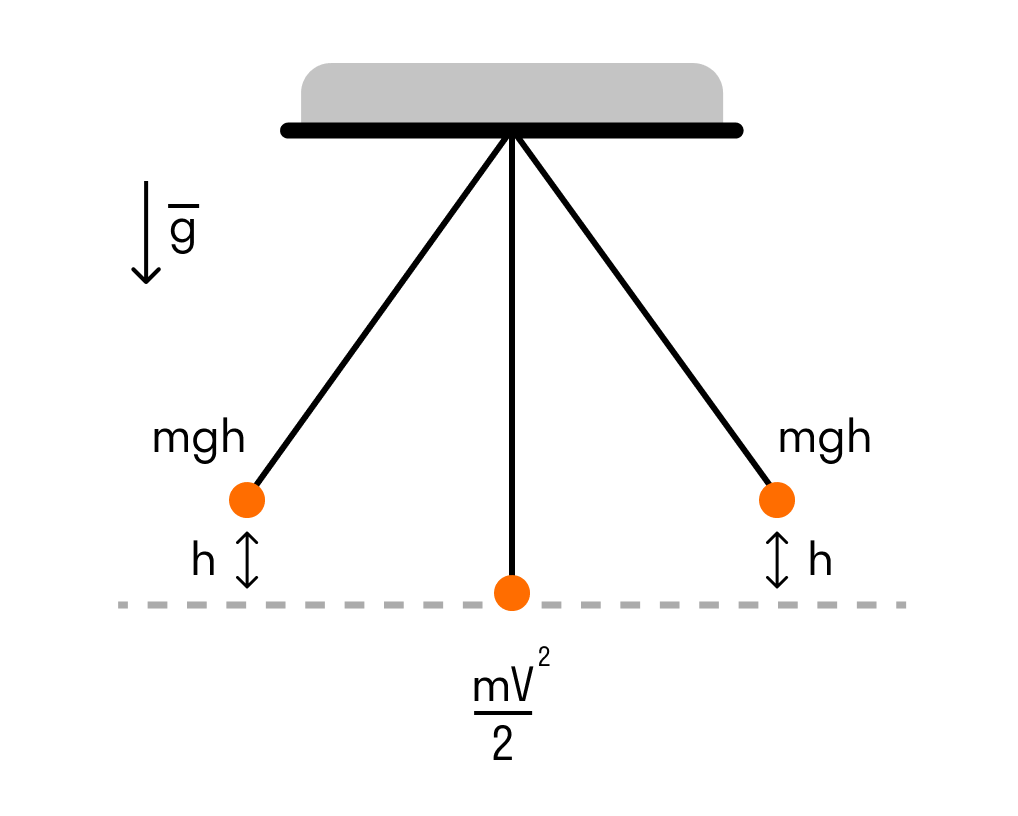
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Определение моментов инерции твердых тел с помощью крутильного маятника
ЛАБОРАТОРНАЯ РАБОТА № 22
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ С ПОМОЩЬЮ
Приборы и принадлежности: лабораторная установка ФМ 15 «Унифилярный подвес», используемая в данной работе как крутильный маятник; блок электронный ФМ 1/1; набор исследуемых образцов.
Цель работы: экспериментальное определение моментов инерции твердых тел с помощью крутильного маятника, проверка теоретических формул расчета моментов инерции твердых тел.
Моментом инерции материальной точки называется величина

где m – масса точки; r – расстояние от точки до оси вращения.
Моментом инерции системы (тела) относительно данной оси называется величина

где n – количество материальных точек в системе; mi – масса i-той материальной точки; ri − расстояние от i-той материальной точки до рассматриваемой оси вращения.
В случае непрерывного распределения масс эта сумма сводится к интегралу

где r − плотность тела.
Момент инерции тела – мера инертности твердых тел при вращательном движении. Его роль такая же, что и массы при поступательном движении.
Момент инерции – величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.
Моменты инерции тел правильной геометрической формы находятся путем интегрирования по (22.3) и являются табличными значениями. Для определения моментов инерции тел сложной формы обычно используют экспериментальные методы, одним из которых является метод крутильных колебаний.
Крутильным маятником называется твердое тело, подвешенное на упругой проволоке и совершающее крутильные колебания относительно положения равновесия.
Крутильный маятник установки ФМ-15 представляет собой металлическую рамку, в которую можно устанавливать исследуемый образец – тело, момент инерции которого нужно найти. На рамку можно также устанавливать (и снимать) массивные грузы m1 (рис. 22.1а). Вся система подвешена на двух натянутых упругих проволоках. Если маятник повернуть на угол a от положения равновесия (рис. 22.1б), а затем отпустить, то он под действием упругого момента проволоки начнет совершать крутильные (вращательные) гармонические колебания относительно положения равновесия.
Выведем закон движения крутильного маятника. Используем основной закон динамики вращательного движения:
где M − момент упругих сил, действующих маятник со стороны проволок; Iм – момент инерции маятника относительно оси вращения ОО1; eм – угловое ускорение маятника.
Упругий момент проволоки по закону Гука для деформации кручения пропорционален углу закручивания: М = —Da, где D — модуль кручения проволоки, а знак минус указывает, что момент действует противоположно направлению увеличения угла закручивания a. Если известен закон изменения угла закручивания a(t), то угловое ускорение 
Обозначив 


Уравнение (22.5) является дифференциальным уравнением гармонических колебаний. Из математики известно, что его решение, которое является уравнением гармонических колебаний и уравнением движения крутильного маятника, имеет вид

а его циклическая (круговая) частота связана с периодом колебаний соотношением

Отсюда период колебаний крутильного маятника

Экспериментально определив период колебаний T маятника и модуль кручения D проволоки, по формуле (22.8) можно рассчитать момент инерции твердого тела любой формы относительно данной оси. При этом нужно знать момент инерции рамки, в которую устанавливается твердое тело, который также можно найти экспериментально.
Для определения модуля кручения и собственного момента инерции рамки воспользуемся тем, что легко можно рассчитать момент инерции грузов m1, которые можно устанавливать на рамку или снимать. Рассматривая грузы m1 как материальные точки, получим их момент инерции относительно оси вращения 2m1r2.
Период колебаний крутильного маятника в отсутствие грузов m1 (период колебаний пустой рамки) согласно (22.8) будет

где Iр – момент инерции пустой рамки.
Период колебаний рамки с установленными на ней грузами m1 согласно (22.8) будет

Совместное решение уравнений (22.9) и (22.10) дает следующие выражения для модуля кручения и момента инерции пустой рамки:


Если в пустую рамку (без грузов m1) установить исследуемый образец, момент инерции которого нужно найти, то период колебаний такого крутильного маятника будет

где Iо – момент инерции исследуемого образца.
Решая совместно уравнения (22.9) и (22.13) получим момент инерции исследуемого образца:

Экспериментально определив периоды колебаний 

Согласно определению момент инерции твердого тела зависит от положения оси вращения относительно тела.
Ось, положение которой в пространстве остается неизменным при вращении вокруг нее тела в отсутствие внешних сил, называется свободной осью тела. Можно доказать, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр масс тела оси, которые могут служить свободными осями; они называются главными осями инерции тела.
У однородного параллелепипеда (рис. 22.2) главными осями инерции являются оси О1, О2 и О3, проходящие через центры противолежащих граней.
Моменты инерции относительно главных осей I1, I2, I3 называются главными моментами инерции тела. Зная главные моменты инерции, можно рассчитать момент инерции относительно любой оси, проходящей через центр масс по следующей формуле:

где j1, j2, j3 – углы, которые образует данная ось со свободными осями О1, О2 и О3 соответственно.
В частности, для прямоугольного параллелепипеда момент инерции относительно оси, совпадающей с пространственной диагональю, будет равен

где a, b, c – длины ребер параллелепипеда, параллельные свободным осям О1, О2 и О3, соответственно (рис. 22.2).
Главные моменты инерции прямоугольного параллелепипеда можно найти с помощью интегрирования по формуле (22.3). Главный момент инерции относительно оси О1, проходящей через центр масс и параллельной ребру длины a (рис. 22.2) равен

По формуле (22.17) можно рассчитать момент инерции прямоугольного параллелепипеда относительно любой оси, проходящей через его центр масс и параллельной одному из его ребер, т. к. обозначения ребер a, b, c можно выбирать произвольно.
Главный момент инерции относительно оси О2, проходящей через центр масс и параллельной ребру b (рис. 22.2) равен

Главный момент инерции относительно оси О3, проходящей через центр масс и параллельной ребру c (рис. 22.2) равен

Описание лабораторной установки
Установка (рис. 22.3) состоит из основания 1, на котором укреплена вертикальная стойка (колонка) 2. На ней неподвижно крепятся нижний 3, средний 4 и верхний 5 кронштейны. Верхний и нижний кронштейны предназначены для крепления узлов подвески и натяжения торсиона (стальной проволоки) 6 и 7, с которым связана металлическая рамка 8 с грузами 9, предназначенная для установки исследуемых образцов 10 или съемной мишени 11 (последняя устанавливается в рамку 8 при выполнении на данной установке лабораторной работы №5). На среднем кронштейне 4 нанесена шкала отсчета угла закручивания торсиона (шкала угловых перемещений) и расположены: стреляющее устройство 12 (в данной работе не используется); электромагнит 13, предназначенный для удерживания рамки 8 в исходном положении и ее освобождения (при этом возникают крутильные колебания рамки вокруг вертикальной оси); фотодатчик 14, предназначенный для определения периода колебаний рамки 8 с исследуемыми образцами 10 и без них.
Силу электромагнита 13 можно регулировать винтом 15. Электромагнит может перемещаться вдоль шкалы угловых перемещений по специальной направляющей и закрепляться гайкой, расположенной под электромагнитом.
Исследуемый образец 10 устанавливается в заданном положении между острием 16, расположенным на нижней планке рамки 8, и винтом 17 с острым концом, расположенным на средней планке 18, для чего в исследуемом образце имеются отверстия. Средняя планка 18 может перемещаться вверх и вниз вдоль рамки 8 и фиксироваться на рамке с помощью винтов 19.
На передней панели блока электронного 20 располагаются:
счетчик колебаний 21 – световое табло, на котором высвечивается число n полных колебаний;
секундомер 22 — световое табло, на котором высвечивается общее время колебаний в секундах (время совершения n полных колебаний);
кнопка »ПУСК» 23 – при нажатии кнопки выключается электромагнит 13 и, после пересечения флажком 24 (установленным на рамке 8) луча фотоэлектрического датчика 14, включаются счетчик колебаний и секундомер;
кнопка »СТОП» 25 – при нажатии кнопки останавливаются счетчик колебаний и секундомер и включается электромагнит.
На задней панели блока электронного 20 расположен выключатель »01» (»Сеть») – при включении выключателя на блок электронный подается питание, на табло счетчика колебаний и на табло секундомера высвечиваются «минусы», и включается электромагнит. Далее после пересечения флажком рамки луча фотоэлектрического датчика, включаются счетчик колебаний и секундомер.
. ПРЕДОСТЕРЕЖЕНИЕ. Чтобы не сбить настройку прибора на ноль, запрещается поворачивать рамку 8 на угол больше 40º в любом случае, в том числе и при установке, смене положения и снятии исследуемого образца 10. Не допускать опрокидывание установки (установка имеет всего три опоры). При установке, смене положения и снятии исследуемого образца 10 запрещается сильно тянуть рамку 8 вниз или вверх во избежание обрыва проволоки или выхода ее из мест креплений. Поэтому при перемещении средней планки 18 вверх или вниз (после того как откручены винты 19) нужно давить рукой не только на саму среднюю планку, но и одновременно на верхнюю или, соответственно, на нижнюю планку. При установке, смене положения и снятии исследуемого образца следует выключить блок электронный. Не следует сильно завинчивать винт 17 – в случае заметного проворачивания исследуемого образца 10 относительно рамки 8 для уменьшения проворачивания можно устранить зазор между исследуемым образцом 10 и средней планкой 18. Подключение установки к блоку электронному ФМ-1/1 разрешается только лаборанту в соответствие с паспортом к установке.
Упражнение 1. Определение момента инерции пустой рамки
1. Соблюдая требования раздела «Техника безопасности» осторожно удалите мишень 11 или исследуемый образец 10 из рамки 8.
2. Снимите грузы 9 с рамки 8.
3. Установите электромагнит 13 так, чтобы его ближняя к рамке 8 торцевая плоскость показывала угол примерно 35° на шкале угловых перемещений (электромагнит фиксируется гайкой 16 на рис. 5.3 – см. лабораторную работу №5). Для уменьшения влияния остаточной намагниченности на колебания рамки сердечник электромагнита должен входить немного вовнутрь электромагнита (положение сердечника регулируется винтом 15).
4. Убедитесь, что флажок 24 рамки пересекает оптическую ось (луч) фотодатчика 14. Если средний кронштейн 4 находится так низко, что флажок 24 не закрывает окошко фотодатчика, поднимите средний кронштейн, отвернув предварительно зажим для его фиксации на вертикальной стойке 2.
5. Убедитесь, что флажок красного цвета на рамке показывает на ноль шкалы угловых перемещений (рамка находится в исходном положении). Небольшое несовпадение красного флажка на рамке с нулем шкалы можно устранить малым поворотом среднего кронштейна 4 вокруг вертикальной стойки 2.
6. Включите установку в сеть, нажав кнопку »01» (»Сеть») на задней панели блока электронного 20. При этом на табло секундомера и счетчика колебаний появятся «минусы».
7. Отклоните рамку на угол 30° и зафиксируйте ее с помощью электромагнита.
8. Нажмите кнопку «ПУСК» блока электронного.
9. По показаниям секундомера и счетчика колебаний блока определите значение времени tр десяти колебаний (nр=10) рамки (пустой рамки − без грузов 9 и без исследуемого образца 10), нажав на кнопку «СТОП», когда на табло счетчика колебаний появится число 10. Результат измерения занесите в табл. 22.1.
10. Повторите 5 раз измерения по пп. 7-9. После нажатия кнопки «СТОП» электромагнит включается.
11. Установите грузы 9 (m1) на рамку и повторите 5 раз пп. 7-9, занося результаты измерения времени tг десяти колебаний (nг=10) рамки с грузами в табл. 22.1.
12. Для одного из замеров определите период 


Упражнение 2. Определение главных моментов инерции прямоугольного параллелепипеда
1. Снимите грузы 9 (m1) с рамки.
2. Соблюдая требования раздела «Техника безопасности» осторожно установите исследуемый образец 10 в рамку 8 так, чтобы ось вращения проходила через центры симметрии двух противоположных граней параллельно ребру a (ось О1 на рис. 22.2).
3. Повторите 5 раз пп. 7-9 упражнения 1, занося результаты измерения времени tо1 десяти колебаний (nо1=10) рамки с исследуемым образцом (ось вращения параллельна ребру a) в табл. 22.1.
4. Соблюдая требования раздела «Техника безопасности» осторожно переустановите исследуемый образец 10 в рамке 8 так, чтобы ось вращения проходила через центры симметрии двух противоположных граней параллельно ребру b (ось О2 на рис. 22.2).
5. Повторите 5 раз пп. 7-9 упражнения 1, занося результаты измерения времени tо2 десяти колебаний (nо2=10) рамки с исследуемым образцом (ось вращения параллельна ребру b) в табл. 22.1.
6. Соблюдая требования раздела «Техника безопасности» осторожно переустановите исследуемый образец 10 в рамке 8 так, чтобы ось вращения проходила через центры симметрии двух противоположных граней параллельно ребру c (ось О3 на рис. 22.2).
7. Повторите 5 раз пп. 7-9 упражнения 1, занося результаты измерения времени tо3 десяти колебаний (nо3=10) рамки с исследуемым образцом (ось вращения параллельна ребру c) в табл. 22.1.
8. Для одного из замеров определите период 

9. Измерьте штангенциркулем размеры a, b, c ребер параллелепипеда. Для упрощения расчетов рекомендуется расположить образец так же как на рис. 22.2, и ребра обозначить так же как на этом рисунке (в соответствии с их длиной). Результаты измерения занесите в табл. 22.1.
10. Определите массу m исследуемого образца 10 путем взвешивания. Результат измерения занесите в табл. 22.1.
11. По формуле (22.17) рассчитайте теоретическое значение момента инерции 
Упражнение 3. Определение момента инерции прямоугольного параллелепипеда
относительно оси, совпадающей с пространственной диагональю
1. Соблюдая требования раздела «Техника безопасности» осторожно переустановите исследуемый образец 10 в рамке 8, так, чтобы ось вращения совпадала с его пространственной диагональю (рис. 22.3; на рис. 22.2 пространственная диагональ показана жирным пунктиром).
2. Повторите 5 раз пп. 7-9 упражнения 1, занося результаты измерения времени tо4 десяти колебаний (nо4=10) рамки с исследуемым образцом (ось вращения совпадает с пространственной диагональю) в табл. 22.1.
3. Для одного из замеров определите период 













1. При оформлении отчета для каждого эксперимента вычислите средние значения времени 












2. Используя средние значения периодов 


3. Используя найденное значение 









4. По формулам (22.17), (22.18), (22.19) рассчитайте теоретические значения главных моментов инерции 


5. Используя рассчитанные в п. 4 теоретические значения главных моментов инерции 


6. Зная теоретическое 

1. Что называется моментом инерции материальной точки?
2. Что называется моментом инерции твердого тела?
3. В чем физический смысл момента инерции?
4. Что называется крутильным маятником?
5. Запишите основной закон динамики вращательного движения.
6. Запишите закон Гука для деформации кручения.
7. Какие колебания называются гармоническими? Приведите уравнение гармонических колебаний.
8. Дайте определения величин, входящих в уравнение гармонических колебаний.
9. Дайте определение периода гармонических колебаний.
10. Приведите формулу, связывающую период и круговую частоту гармонических колебаний.
11. Запишите формулу для периода колебаний крутильного маятника.
12. Чему равен момент инерции грузов m1?
13. Что называется свободной осью тела?
14. Что называется главными осями инерции тела?
15. Что называется главными моментами инерции тела?
1. Курс физики: учеб. пособие для вузов. – М.: Издательский центр «Академия», 2007, § 16, с. 34-36; § 18, с. 37-38; § 20, с. 40-42; § 140-142, с. 253-258.
2. , Курс физики: Учеб. пособие для втузов. – М.: Высш. шк., 2000, § 4.2, пп. 1-4, с. 50-52; § 4.3, пп. 1-4, с. 53-56; § 27.1-27.2, с. 358-363.
3. Курс общей физики: в 4 т. Т. 1. Механика. Молекулярная физика и термодинамика: учебное пособие / ; под общ. ред. . – М.: КНОРУС, 2009. § 5.3-5.5, с. 154-172; § 8.1, с. 258-259; § 8.4-8.5, с. 267-275.
4. Общая физика: руководство по лабораторному практикуму: Учеб. пособие / Под ред. и . – М.: ИНФРА-М, 2010. Задача № 10, с. 86-91.
http://skysmart.ru/articles/physics/garmonicheskie-kolebaniya
http://pandia.ru/text/78/385/1344.php