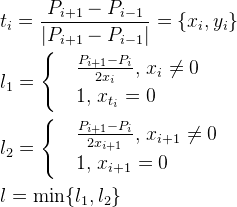Интерполяция данных: соединяем точки так, чтобы было красиво
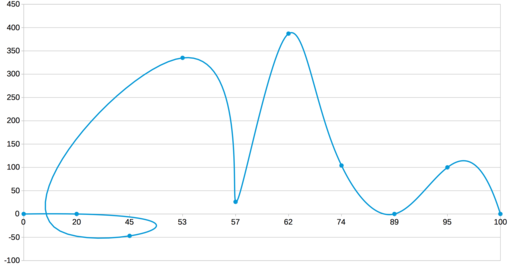
Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти
Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1 .  Pn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
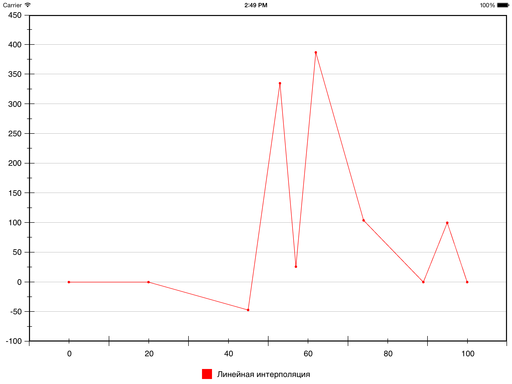
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):
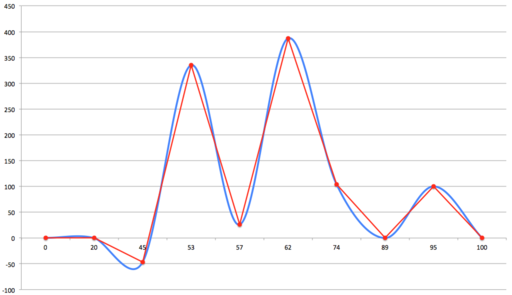
Результат линейной интерполяции этих точек выглядит так:
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.
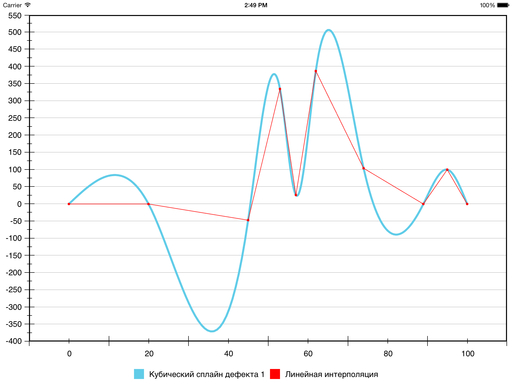
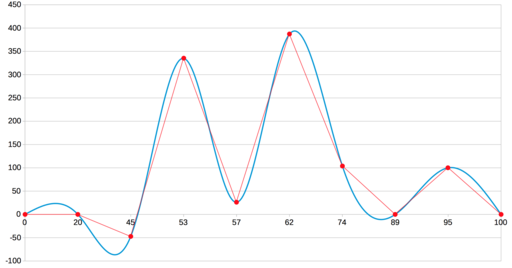
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:
Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.
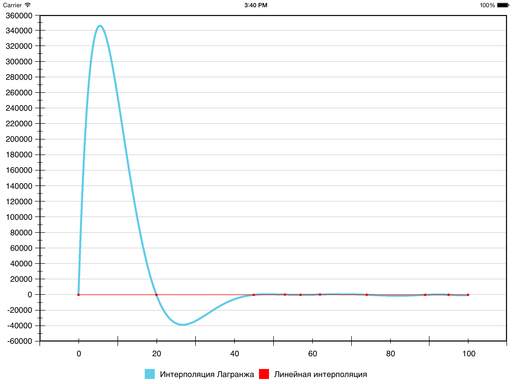
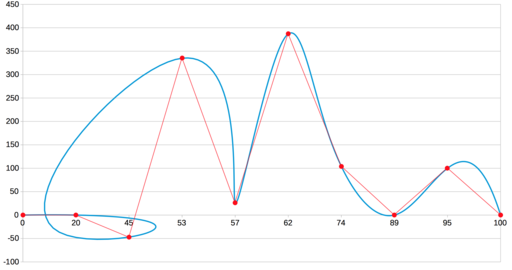
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:
Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:
Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.
Думаем и экспериментируем
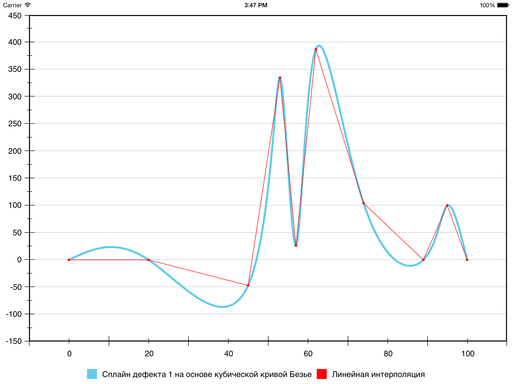
Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
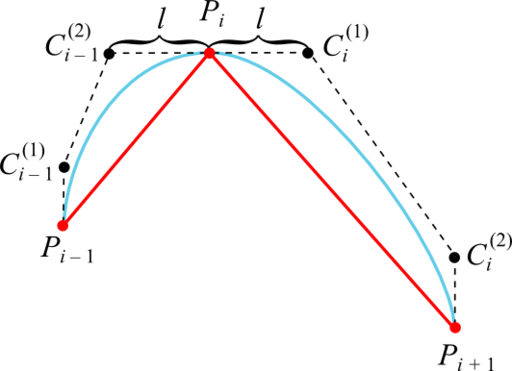
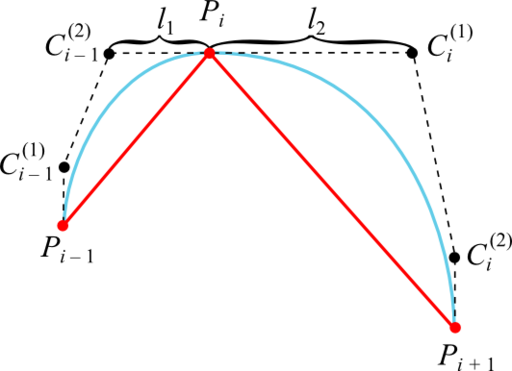
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:
В качестве прямых, на которых лежат точки Ci – 1 (2) , Pi и Ci (1) , целесообразно взять касательные к графику интерполируемой функции в точках Pi. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:
Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C1 (1) и Cn – 1 (2) совпадают с точками P1 и Pn соответственно).
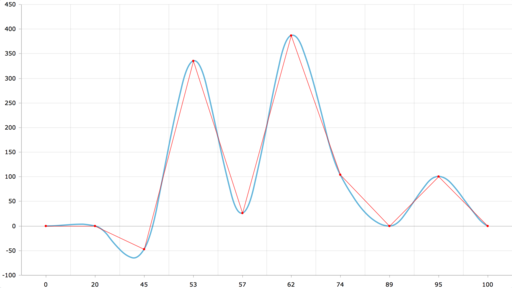
В этом случае получается вот такая кривая:
Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.
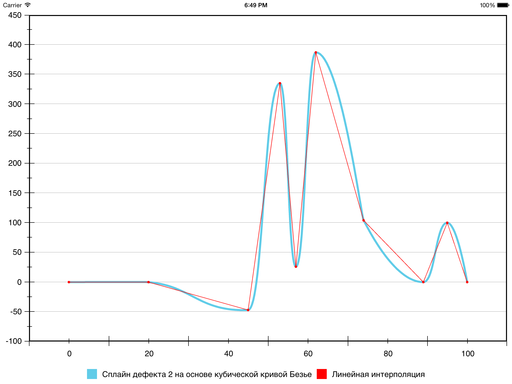
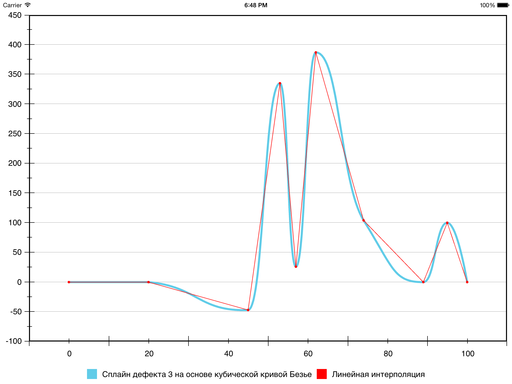
К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1 (2) и Ci (1) , но при этом сохраняем их все лежащими на одной прямой:
Эвристика для вычисления расстояний будет такой:
Результат получается такой:
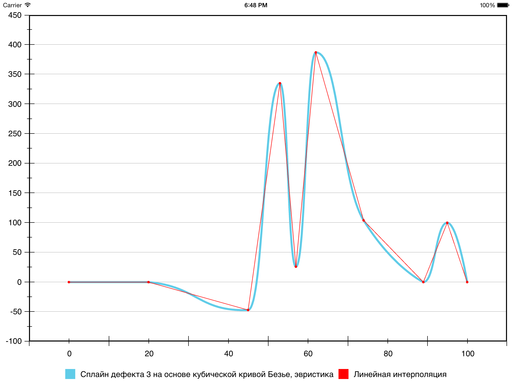
В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Результат следующий:
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.
А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.
MS Excel
Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.
Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂
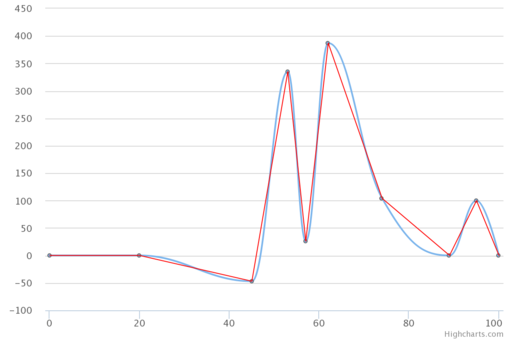
Highcharts, одна из самых популярных JS-библиотек для построения диаграмм
Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека
Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X
Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.
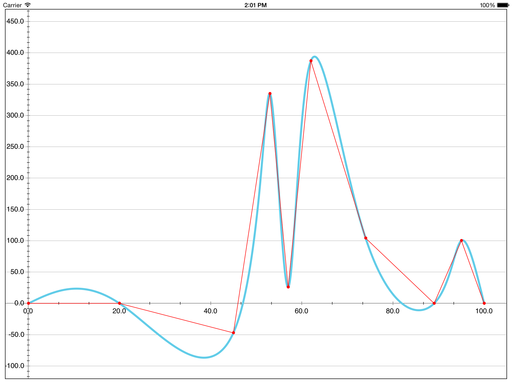
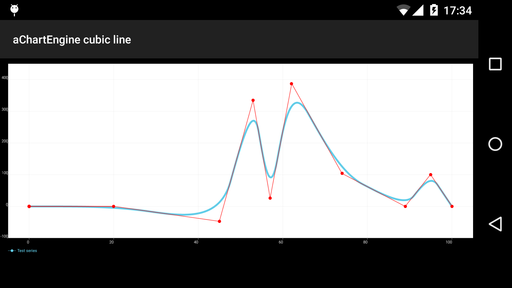
aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Аппроксимация функции одной переменной
Калькулятор использует методы регрессии для аппроксимации функции одной переменной.
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
Линейная регрессия
Коэффициент линейной парной корреляции:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
,
где
Средняя ошибка аппроксимации:
Кубическая регрессия
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Степенная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Логарифмическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Экспоненциальная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида частные производные равны:
,
Подставив производные, получим:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Расчет кривой второго порядка на плоскости по точкам
| Элементы кривой второго порядка или координаты |
| Уравнения Ax^2+By^2+Cxy+Dx+Ey+F=0 |
| A= |
| B= |
| C= |
| D= |
| E= |
| F= |
| Полученная формула | ||||||||||||||||||
| Коэффициенты через пробел Калькулятор предназначен для расчета и создания уравнения кривых второго порядка на декартовой плоскости по нескольким точкам, от двух до пяти. Не является секретом то, что уравнение кривой второго порядка может быть представлена формулой Мы будем использовать чуть измененную формулу, разделив все коэффициенты на a6 отсюда видно, что кривую второго порядка можно однозначно определить по пяти точкам. Кривая второго порядка при различных коэффициентах может превращатся в следующие «типы»: — пара пересекающихся прямых — пара паралельных несовпадающих прямых — пары совпадающих прямых — линии, вырождающиеся в точку — «нулевые линии», то есть «линии», вовсе не имеющие точек Если Вам интересны формулы при которых получаются все эти типы, то пожалуйста — пара пересекающихся прямых — пара параллельных прямых — пара совпадающих прямых Этот сервис позволяет Вам по заданным точкам определить, какую же кривую второго порядка провести через эти точки. Кроме этого, Вы увидите все основные параметры полученной кривой второго порядка. От Вас лишь понадобится предоставить боту от двух до пяти декартовых координат, что бы бот мог решить эту задачу. ИНВАРИАНТЫ И СВОДНАЯ ТАБЛИЦАЛюбая кривая второго порядка характеризуется тремя инвариантами, имеющими вид И одним семиинвариантом если Вам интересно, откуда они появились, то рекомендуем прочитать книгу «Аналитическая геометрия — Делоне» Характеристическое уравнение кривой второго порядка: Таким образом сводная таблица имеет вид
Анализируя написанные онлайн калькуляторы по этой теме, нашел интересную «особенность». Попробовав рассчитать по трем точкам кривую второго порядка, зная что эти точки принадлежат окружности, я с завидным постоянством получал ответ, что графиком(формой)полученного уравнения кривой является эллипс. Нет формально, конечно стоит признать что окружность является частным примером эллипса, но ведь можно пойти дальше и признать что и эллипс и гипербола и парабола, являются лишь частным примером кривой второго порядка общего вида, и в ответах таких калькуляторов выдавать ответ пользователю «вы получили уравнение второго порядка» и всё. не соврали же. Такое сверхлегкое трактование и смешение определений геометрических фигур, никак не способствует пониманию и сути решаемых задач. Это как в анекдоте «А теперь нарисуем квадрат со сторонами 3 на 4″(с) И не поймешь то ли рисовать квадрат, то ли прямоугольник. СИНТАКСИСJabber: kp2 Строкой является список чисел разделенное пробелами. А каждое «число» представляет собой абсциссу и ординату точки разделенные двоеточием. Координат или их «замен» должно быть ровно шесть То есть если мы знаем пять координат то 6 элементом у нас будет единица. В вкладке Пример Вы сможете увидеть решения некоторые. Если в строке есть числа не имеющие : то это означает что это неизменяемый соответствующий коэффициент кривой второго порядка. Например если в строке стоит ноль на первой позиции строки то это означает что A1=0 Бот вычисляет численные параметры кривой. Если же Вам надо нарисовать кривую второго порядка на плоскости, просьба использовать программу GeoGebra и материал Построить график функции c помощью GeoGebra ПРИМЕРЫНачнем сразу с проверочного примера Вообще, убедимся правильно ли считает бот? Итак, есть у нас функция x*x+3x-11=y определим значения при x=1,2,3,4,5 значения получились такие y=-7,-1,7,17,29 и зададим эти точки в качестве исходных пишем kp2 1:-7 2:-1 3:7 4:17 5:29 в результате получаем следующее: На первый взгляд получилось далеко не то, что должно получится. Но если мы уберем нулевые коэффициенты, и разделим все на 0.09091 то результат будет такой то есть Что и требовалось доказать в качестве правильности расчетов нашего бота. Теперь пусть у нас есть всего лишь три точки С координатами x=1,2,3 и y=-7,-1,7 Логично, что это тоже самое уравнение параболы что мы разбирали в первом примере. НО! при трех точках такое решение не единственное. Давайте попробуем задать боту всего три координаты и скажем ему какого вида уравнение мы хотим получить. Это частное уравнение кривой второго порядка в котором коэффициенты а1 и а5 равны нулю Скажем об этом боту kp2 0 1:-7 2:-1 3:7 0 1 где 0- показывает какие коэффициенты нам НЕ надо учитывать, а 1 — это постоянный коэффициент, то есть его находить нет необходимости. Он известен. Видим что не учитываем 1 и 5 коэффициент. Кривая второго порядка a1*x*x+a2*y*y+a3*x*y+a4*x+a5*y+a6 = 0 источники: http://planetcalc.ru/5992/ http://abakbot.com/ru/online-2/krivaya-two |