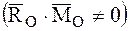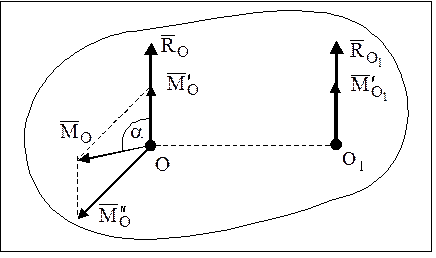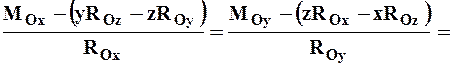Получить уравнение центральной винтовой оси

Уравнение центральной винтовой оси

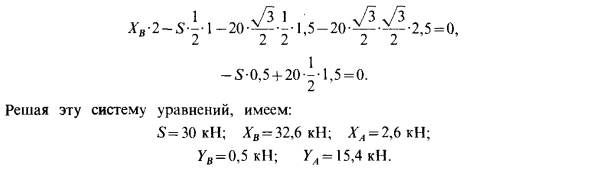
Уравнение центральной винтовой оси

• Предположим, что главный вектор Lo проецируется на координатные оси Rx, Ry и Rz, а главный момент Lo получается на проекции Lx и Ly с центром редукции ^ в качестве начала координат. Когда система сил движется к центру редукции O (рис. 78), обнаруживается динамо с главным вектором A, = A и главным моментом LOl. Векторы LO1 и A, как генераторы динамо, параллельны, поэтому отличается только скалярный коэффициент k0. У нас есть Lo-k0R, _ _ (9) Согласно (2), поскольку Rt = R, основные моменты LOi и Lo удовлетворяют следующему соотношению: EOi = Lo

OO, xR. (2 ‘) Подставляя LOi из (2 ‘) в (9) Lo-Od, xR = knR. (9 ‘) Координаты точки O, из которой получается динамо, обозначены x, y, z.

Тогда проекция вектора OOt на оси координат равна координатам x, y, r. Учитывая это, (9 ‘) можно выразить в следующем виде: (Lxi + Lj + LZE) -x Jy AH A, = k0 (Rxi + Ryj + Rjc), Aj Где i, j и А — единичные векторы векторного произведения осей координат и OO, а x A выражается определителем. Векторное уравнение (9 «) соответствует трем скалярным уравнениям и может быть выражено следующим образом после отбрасывания Lo: £, — (yY, -? I,) _ £, — (rY, -xY,) _ I, I, (9 «) Рисунок 78 Рис. 79 Линейное уравнение (10) для координат x, y и z является уравнением спиральной оси с линейным центром. Таким образом, в точке, где система сил сводится к двойственности, есть прямая линия. Пример 1.

Такая линеаризация, конечно, в некоторой степени искажает действительное изображение движения, но чем меньше отклонение системы от устойчивого положения равновесия, тем точнее получается линеаризованное изображение. Людмила Фирмаль

В конце куба с длиной стороны 1 = 3 м действуют силы Fj = Fr = 2_H и F3 = l H (рис. 79). Приносит систему питания F, F2. Е3 в простейшем виде. Решения. Выберите точку O (начало координат) в качестве центра уменьшения силы и рассчитайте главный вектор R и главный момент Lo. для Проекции на оси этих векторов K = Y.Fix = F2 = 2B; Rr ​​= ^ Flt = F3 = i H-. Rn- £ /? = £, = 2 H; ix = XWx (F;) = 0; Координаты у нас есть: Z.z = £ m, (F) = F3 / -F2 / = -3Hm.

Значение основного вектора и значение главного момента составляют R = ^ R2x + R ^ + R ^ = y / 9 = 3 Н. £ 0 = V / ZJ + ZJ + IJ = V / 45 = 6,8 Нм Определите угол a между векторами Eo и R. Для этого сформируем скалярное произведение. Это выражается в двух формах: Eo-R = LoRcos

• Один конец — это сечение _A, и нормальная сила P прикладывается в точке B (рис. 81, а). Надежно прикрепите балку CD к балке AB секции C под прямым углом. На конце балки I в плоскости, параллельной координатной плоскости Ayz, действует пара сил с моментом M = Ra. Направление вращения пары размеров и сил показано на рисунке. Определяет момент силы пары вложенных сил. Решения. Лучи B и CD, рассматриваемые вместе, освобождаются от галстуков. Вложение системы пространства сил создает неизвестную силу Ra, спроецированную на ось координат силы X с вектором. Момент Отологон Динат М.Л., (Рисунок £ Flx = 0; * l = 0; £ f (, = 0; ya = Q; £ F „= 0; ZA — P = O; Y.

Для того, чтобы определить силу реакции упорного подшипника, п Людмила Фирмаль

Что касается проекции сил на оси координат, то здесь есть следующее. EG (x = 0;% 4 + Uv-Psin asin p-Ssiny = 0; 1 EFf = 0; Ul + rB + Pcosa-Scosy = 0;> EF (, = 0; Z4-Psin acos P = 0. При определении проекции силы P на оси координат сначала разбейте ее на две вертикальные составляющие. Одна параллельна оси Oy и имеет проекцию на эту ось P = Pcosa. Вертикальный компонент расположен в плоскости оси и имеет проекционное значение в этой плоскости. (А) Спроецируйте силу P как вектор на оси Ax и Ar. В P, = -P „sin p = -Psin a sin p; P, = P„ cosp = Psinacosp.

За момент силы вокруг осей получим … МЖ (Р,) = О; -Gv (/, + / 2) + Scosy /, -Pcosa (Z, + / 2 + / 3) = 0;] EM, (A) = 0; XB (Z, + / 2) -Ссины / 1- Я -Psin acos pZ „-Psin asin p (Z, + 12 + Z3) = 0; EA / I (F,) = 0; -SP + PcosaZ4 = 0. По определению, при расчете момента силы вокруг координатной оси, спроецируйте силу на плоскость, перпендикулярную оси, и рассчитайте момент проекции силы относительно пересечения оси и плоскости. Сила, параллельная или пересекающая ось, дает нулевой момент вокруг этой оси.

При определении момента силы S для осей координат он разлагается на компоненты, параллельные осям координат, вычисляет момент каждого компонента для соответствующих координатных осей на основе теоремы Баринона и добавляет их алгебраически. Значения составляющих сил равны проекции этих сил на оси и могут быть получены из уравнения (а). Момент силы R. рассчитывается аналогично. Решите систему линейных уравнений (а) и (б) для проекции неизвестных сил. Могу решить Подставляя уравнение (а) и угол, оно становится следующим.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Приведение системы сил к динаме

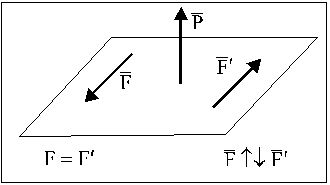
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом (рис. 30) .

Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме (рис. 31).

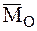
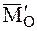
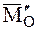
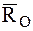
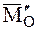
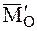
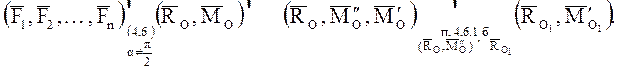
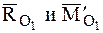
Разложив на две составляющие — вдоль главного вектора и — перпендикулярно главному вектору, для и будем иметь случай 4.6.1б. Вектор , будучи свободным вектором, переносится параллельно самому себе в точку О₁):

Вектора представляют собой динаму,

где , .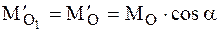

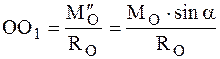
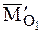
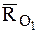
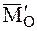
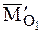
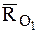
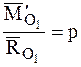
В рассматриваемом случае приведения системы сил главный момент имеет минимальное значение. Причем это значение момента сохраняется при приведении заданной системы сил к любой точке, лежащей на линии действия главного вектора и главного момента (рис. 31). Уравнение этой линии, называемой центральной (осью динамы), определяется из условия коллинеарности векторов и :

. (4.27)

В соответствии с соотношениями (4.16) и (4.17)

,

,

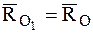
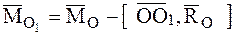
тогда уравнение центральной оси динамы в векторной форме можно записать так:

.

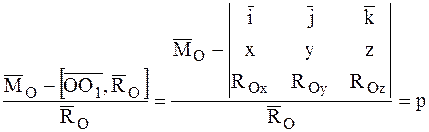
Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:

. (4.28)

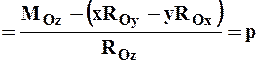
Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.

4.7. Алгоритм решения задач по приведению систем сил к простейшим системам – схема алгоритма

Дата добавления: 2015-08-01 ; просмотров: 2410 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Получить уравнение центральной винтовой оси

Рама. Составная конструкция (2a). Заделка-шарнир-подвижный шарнир. Анимация и графика П.Горшкова.

Рама. Составная конструкция (2b). Два шарнира и скользящая заделка. Анимация и графика П.Горшкова.

Цепь . Определяем положение равновесия. Анимация и графика П.Горшкова.

Задача на теорему о трех силах. . Определяем реакции опор. Анимация и графика П.Горшкова.

Составная конструкция (3 тела, шарнир) . Определяем реакции опор. Анимация и графика П.Горшкова.

Составная конструкция (3 тела, шарнир, стержень) . Определяем реакции опор. Анимация и графика П.Горшкова.

Составная конструкция.Нагрузка, распределенная по дуге. ТФ-05-13, 21.2.2014.

Ферма

Трение

Задача на трение качения (3 тела) . Определяем условие равновесия системы. Анимация и графика П.Горшкова.

Задача на трение скольжения. Определяем условие равновесия рамы. Анимация и графика П.Горшкова.

Задача на трение скольжения . Определяем условие равновесия рамы + некоторые рассуждения на общие темы.

Пространственная система сил. Задачи

КИНЕМАТИКА

Пятизвенник. Уравнение трех угловых скоростей и ускорений

Четырехзвенник. Уравнение трех угловых скоростей (1)

Четырехзвенник. Уравнение трех угловых скоростей (2)

Планетарный механизм. Метод графов и метод МЦС

Угловые скорости многозвенного механизма. Эффективное решение с помощью уравнения трех угловых скоростей

Сложное движение точки. Ускорение Кориолиса. Вывод формулы

Сложное движение точки. Ускорение Кориолиса. Правило Жуковского

Сложное движение точки. Абсолютное ускорение. Задача

Сложное движение точки. Задача о муфте/Ускорение (ТФ-05-13)

Сложное движение точки. Задача о качающейся муфте (К13,3). Программа для Maple

Сферическое движение. Кинематические уравнения Эйлера в проекции на подвижные оси

3D кинематика. Решение задачи о треугольнике

3D кинематика. Параллелепипед с шарнирной крышкой

ДИНАМИКА

Кинетическая энергия. Решение задачи Д2 (приведенные массы)

Теория удара

Удар в зубчатой передаче. (Лекция 15 мая 2015 г. ИТАЭ, МЭИ)

Колебания, устойчивость и др.

Два груза на балке Лекция 11.9.2015 в гр. С-12-11

Стабильность Лекция 5 мая 2015 в гр. ЭР-16-12

Экзаменационная задача в МЭИ. Решение задачи на составление уравнения Лагранжа 2-го рода

1. Два цилиндра, пластина, стержни.

2. Брусок, цилиндр сверху, шток и стержень. Простая задача.

3. Используем теорему о сложении скоростей.

4. Задача с муфтой. Используем метод прямого дифференцирования.

5. Задача с линейной обобщенной координатой. Цилиндр, клин и муфта.

6. Задача с параллелограммом.

7. Кривошип, два цилиндра, наклонный стержень, муфта

8. Цилиндр, закрепленный шарнирно на ободе, брусок и пластина между ними

9. Цилиндр, наклонная плоскость, пресс и пластина между ними. Линейная обобщенная координата

10. Невесомый прямоугольный уголок, скользящий по ребрам неподвижного бруска.

11. Блок из колес с неподвижной осью, груз на наклонной плоскости. Повернутые оси координат. Линейная обобщенная координата.

12. Блок из колес с неподвижной осью и цилиндр с подвижной осью. Линейная обобщенная координата.

13. Два цилиндра и груз. Один цилиндр катится по неподвижной поверхности, другой закреплен на ободе первого и катится по грузу.

14. Два цилиндра и соединяющий их стержень

15. Два цилиндра, сверху балка и вертикальный шток