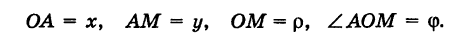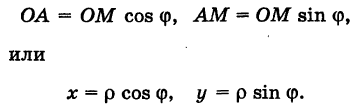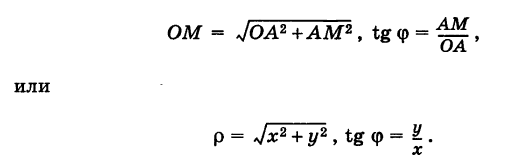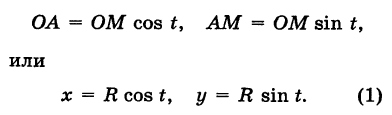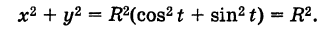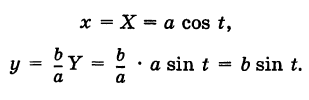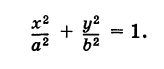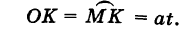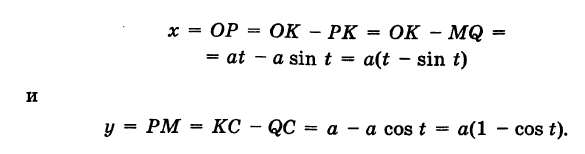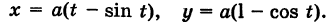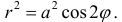Полярная система координат уравнение движения

Полярные координаты — определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

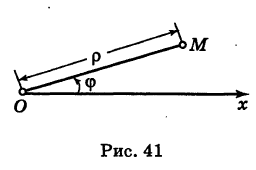
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

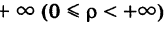
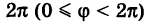
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

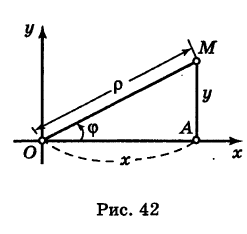
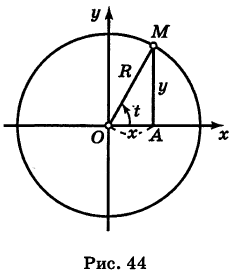
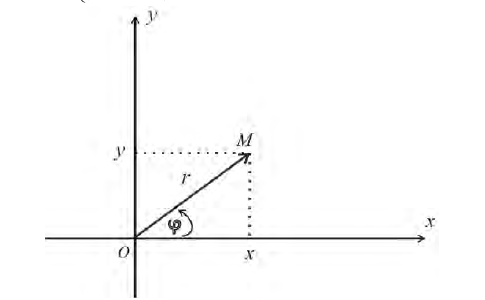
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

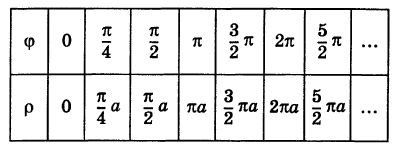
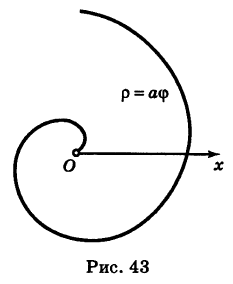
Рассмотрим кривую 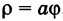, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 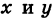, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М 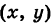— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

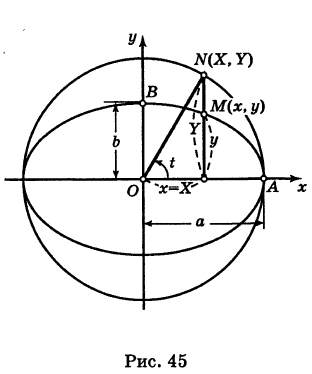
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

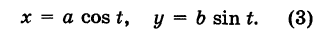
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

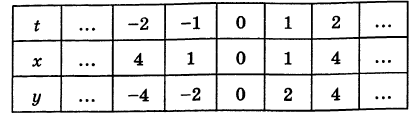
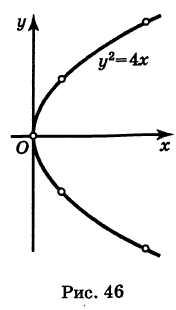
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 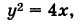т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

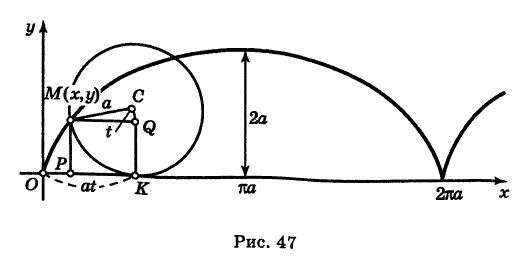
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

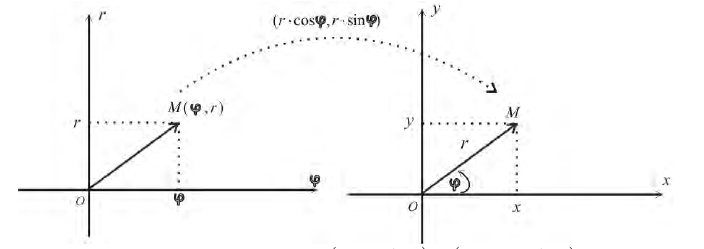
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 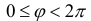. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 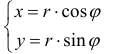(1)

Рис.1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
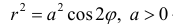
Решение.

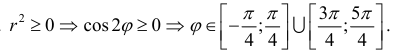
Вычислим значения r при различных значениях ϕ :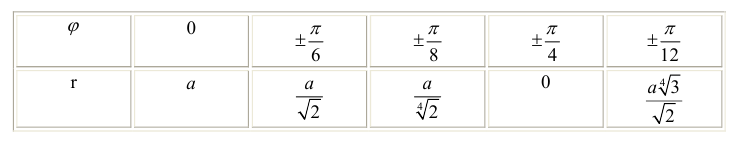

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

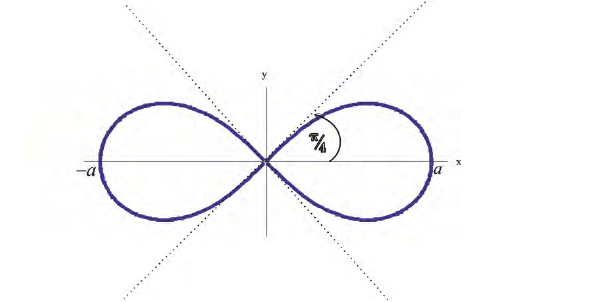
Рис.3. Лемниската

Пример 2.

а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




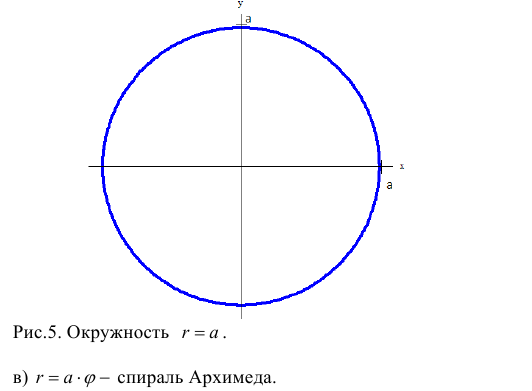
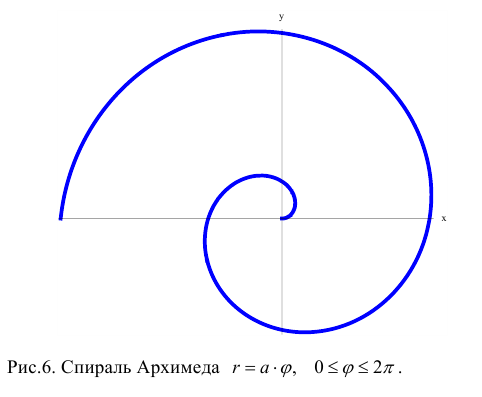
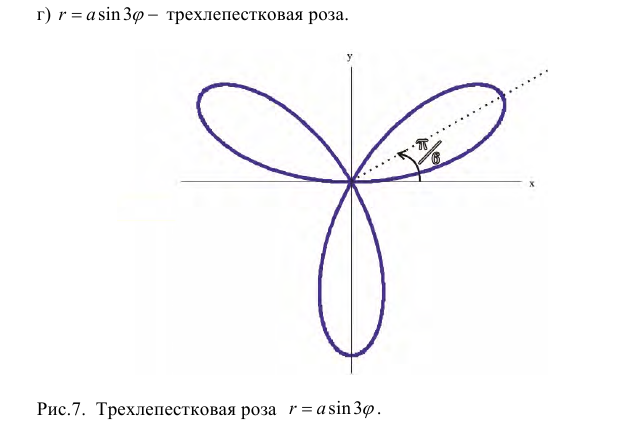
Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

При этом, если r > 0, то векторы 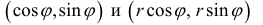сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Скорость и ускорение точки в полярных координатах

Скорость и ускорение точки в полярных координатах

• Рассмотрим движение точек на плоскости. В этом случае движение может быть задано в полярных координатах. Для этого возьмите точку O на плоскости в качестве полюса и нарисуйте от нее полярную ось, например, ось быка (рис. 22). Если радиус-вектор r и полярный угол = f2 (t) — (23). Полярный угол считается положительным, если он простирается от полярной оси против часовой стрелки до радиус-вектора. Радиус-вектор как расстояние от точки О до точки М принимает только положительные значения.

Уравнение (23) называется уравнением движения для полярных точек. Это также параметрические точечные траекторные уравнения. Исключение параметра-времени t из (23) дает орбитальное уравнение в полярных координатах. F (r, r = rr °, gr = gfr °. Для проекции скорости на ось, положительное направление которой совпадает с направлением единичного вектора r ° и jr с (24), vr = r, gr = gf. (26) Их называют лучевой и боковой скоростями соответственно. В зависимости от знака производной мицелия лучевая и боковая скорости являются как положительными, так и отрицательными. Используйте (24), чтобы определить ускорение точки в полярных координатах. У нас есть a = dv / dl = (d / d /) (rr 0 + gfr °).

Потенциальная энергия N материальной точки в мыслимой точке силового поля M осуществляется силой поля, действующей на материальную точку при перемещении из точки M в начальную точку Mo, т. Людмила Фирмаль

Проведите дифференциацию и получите a = rf ° + r + r fr 0 + r fr 0 + r f. Для производной по времени единичного вектора p ° dp0 / d ^ = φ (-r0), Вектор p ° вращается с той же угловой скоростью φ, что и вектор r °, поэтому единичным вектором, на который направлен вектор dp ° / dt, является вектор (-r °). Ускоряя производную единичного вектора и подставляя ее в уравнение, объединяющее члены, получаем в = (r-rf2) r ° + (rf + 2rf) p °. (27) Получены точечные ускорения разложения на радиальные ар и боковые ап компоненты. a = a, + ap, ar = (r-rf2) r °, ar = (rf + 2rf) p °. Для проекции ускорений на оси Or и Op получаем a, = r-rp2, ap = rp + 2rp. (28).

Ускорение ar называется радиальным, поперечным направлением. Боковое ускорение также может быть выражено в следующем формате: Эта формула для бокового ускорения широко используется при рассмотрении движения планет и искусственных спутников Земли. Рисунок 23 Равные производные по Поскольку радиальная и боковая составляющие ускорения перпендикулярны друг другу, Для фиксированных координатных осей Ox, Oy и Oz формула ax = dvx / dt, ay = dvy / dt, a2 = dv: / dt. Для подвижных осей Or и Op, как видно из (26) и (28), a и ap не являются временами от vr и vp. Особый случай.

• В этих уравнениях φ — угловая скорость вращения радиус-вектора, а φ — его угловое ускорение. Пример 1. Движение точки — это уравнение r = / (l + COSOH), φ = ШГ, Где я и со постоянные значения. Определить скорость и ускорение точки в полярных координатах траектории уравнения, времени t и момента Решения. Из уравнения движения уберите следующее уравнение для орбиты в полярных координатах: r = f (1 + C0 $ f). Это кардиоидное уравнение (рис. 24).

Проекции скорости и ускорения на полярную ось определяются уравнениями (26) и (28). У нас есть: Мы получаем «, = / = — / Eosin South. 1> = Гф = / ш (1 + COSO) /), t> = + = к ^ 2 (1 + 008 J = ^ 39» 6,2 м / с Прогноз ускорения всегда определяется по формуле а = -2 м / с2; ау = -6 м / с2; а =. > / ai + a * = s / 40×6,3 м / с2, ускорение геля n -2coszsinz + 36-2sin2 (i Ускорение при 2 ^ / 16 cos2 / + 36 sin2 2 / — ^ / 3 / 5® — 0,3 м / с. Далее для r = n / 6 с Скорость предопределена Боковая скорость при =, л / 6 с — по формуле х = 4sin / | Координаты движущейся точки при t = n / 6 на / 6 / 6м. y = 3cos2r | / 6 = 1,5 м. Отметьте положение движущейся точки на траектории в соответствии с координатами, выберите масштаб и нарисуйте векторы скорости и ускорения из проекции на ось.

Таким образом, принцип возможного смещения не является в действительности активной силой, и помимо сил реакции идеального соотношения, для которых задача не определена, определяются все силы энергосистемы. Людмила Фирмаль

Для радиальной составляющей скорости в рассматривается направление, противоположное единичному вектору r °. Это потому, что v был найден со знаком минус. Только числовое значение определяется для боковой составляющей скорости. Из рисунка 25 видно, что направление вектора противоположно направлению единичного вектора p ° (направление p ° получается поворотом вектора r ° на 90 ° против часовой стрелки). Следовательно, в рассматриваемом случае вы должны использовать знак минус для vp, то есть c, = -b, 2 м / с.

Для проверки правильности определения vp вы можете использовать следующую формулу «F. Нормальное ускорение всегда направлено внутрь вогнутой поверхности дорожки. Оказывается, что направление тангенциального ускорения а определяется а и направлено вдоль вектора скорости. В результате точка в определенной точке ускоряется. Определить радиус кривизны орбиты в момент времени t = 1/6 с. Все необходимые для этого количества уже доступны. получить = — = 39/5 «7,8

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Полярная система координат (полярные координаты)

Полярная система координат на плоскости — это совокупность точки , называемой полюсом , и полупрямой , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки в полярной системе координат определяется расстоянием ( полярным радиусом ) от точки до полюса (т.е. ) и углом ( полярным углом ) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , называемыми главными значениями полярного угла . В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где . В этом случае значениям полярного угла для всех соответствует одно и то же направление радиус-вектора.

С полярной системой координат можно связать прямоугольную систему координат , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат <связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты точки , отличной от точки , и ее полярные координаты . По рис.2.28,б получаем

Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

Последние два равенства определяют полярный угол с точностью до слагаемых , где . При из них следует, что . Главное значение полярного угла находится по формулам (рис.2.29):

Пример 2.9. В полярной системе координат :

а) изобразить координатные линии ;

б) изобразить точки с полярными координатами . Найти главные значения полярных углов этих точек;

в) найти прямоугольные координаты точек .

Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии и — полупрямые (рис.2.30,а).

б) Построим точки и (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение . Следовательно, это одна и та же точка, которая совпадает с точкой , изображенной на рис.2.30,а.

в) Учитывая пункт «б», найдем прямоугольные координаты точки . По формулам (2.17) получаем:

1. Главное значение полярного угла можно выбрать иначе, например, .

2. Расстояние между двумя точками и (длина отрезка ) вычисляется по формуле

что следует из теоремы косинусов (рис.2.31).

3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах и , находится по формуле

Она положительна, если (при этом ориентация пары радиус- векторов и правая), и отрицательна, если \varphi_2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEcAAAASBAMAAAD73d5oAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAwPxBoV0BgTEhELHR4JFxAbyQhgAAASJJREFUKM9jYCAdsEYRoyqmCqvwUgYGa1E4jy3mJczQCQzLRRZAOY8ZWBUPTUCoCvSEMGYzcJ0VcoCwOQUY1jZwFyAZbegBppwZ+Bw41CBC/AFALjuyIgZrCZCJxxgmMjBAFTFO4NrAwGLAwIlQNAWkiNkB6BCgNcYgZzE2sAYw9CSYX0cYJJwAVsQmwMAdsO7LDSCHbxt3A8dlhpniMIdDncSlwbGB7SHDbwZHEOdskalTAAMDTFEM1HMMnxyda6UYPjEUgThLlJRAeqGK4MHEwHpJ6T6I9gHzvNsY4IpYkQK8yQrkNg4NMEefAaEIGXwCqWFY2ADWrIxD0UGw+yVYQRS7Gg5FYBv4gq3B8QKONzvdSnRFBmA7lRQJJx22NKDLACxqN6Lf3w5xAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> (ориентация пары радиус-векторов и левая).

Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:

а) скалярное произведение ;

б) длину отрезка ;

в) внешнее произведение ;

г) площадь треугольника ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

Площадь положительная, так как векторы и образуют правую пару .

г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах и .

д) По формулам (2.17) находим прямоугольные координаты точек и :

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

Пример 2.11. На координатной плоскости отмечена точка . Найти:

а) полярные координаты точки , образа точки при повороте радиус-вектора на угол вокруг начала координат (рис.2.33);

б) полярные координаты точки , образа точки при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).

Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:

так как точка лежит в четверти.

При повороте радиус-вектора вокруг полюса на угол полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки : , , причем — главное значение полярного угла .

б) При инверсии относительно окружности радиуса полярные координаты образа выражаются через полярные координаты прообраза следующими формулами:

Поэтому, учитывая пункт «а», находим (для ):