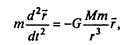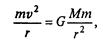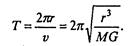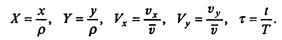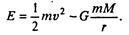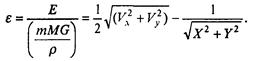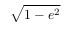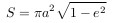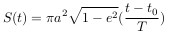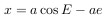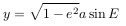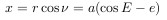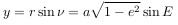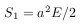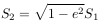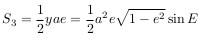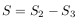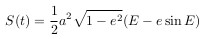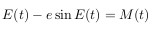Полярное уравнение кривой для двух небесных тел

Тема 4: Моделирование движения небесных тел. Задача Кеплера

Как движется Земля и другие планеты в пространстве? Что ждет комету, залетевшую из глубин космоса в Солнечную систему? Многовековая история поиска ответов на эти и другие вопросы о движении небесных тел хорошо известна; для многих людей, внесших большой вклад в науку, именно интерес к астрономии, устройству большого мира, был первым толчком к познанию.

Движение планет имеет особое значение, поскольку в прошлом оно сыграло важную роль в формировании механистического взгляда на Вселенную. Немногие теории оказали столь же огромное влияние на западную цивилизацию, как законы движения и всемирного тяготения Ньютона, связывающие в единое целое движение звезд и земных объектов.

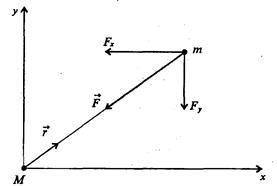
По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Если поместить начало системы координат на одном из тел (размерами тел по сравнению с расстоянием между ними будем пренебрегать), математическая запись силы, действующей на второе тело, имеет вид (см. рис.)

(1)

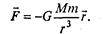
Здесь G = 6,67∙10 -11 м 3 /кг∙с 2 — гравитационная постоянная.

Рис. Выбор системы координат при решении задачи двух тел

Знак «минус» в формуле (1) связан с тем, что гравитационная сила является силой притяжения, т.е. стремится уменьшить расстояние r между телами.

Далее мы ограничимся лишь изучением взаимного движения двух тел. При этом возникает непростой вопрос: с какой позиции (в какой системе координат) изучать это движение? Если делать это из произвольного положения — например, наблюдатель с Земли изучает взаимное движение Солнца и планеты Юпитер — задача станет для нас слишком сложной. Ограничимся лишь простейшей ситуацией: рассмотрим движение одного из тел с точки зрения наблюдателя, находящегося на втором, т.е., например, движения планеты или кометы относительно Солнца, Луны относительно Земли, пренебрегая при этом относительно небольшими силами притяжения от всех прочих небесных тел. Разумеется, мы тем самым произвели ранжирование факторов, и наши последующие действия имеют отношение к реальности лишь в меру соблюдения определенных условий.

Уравнение, описывающее движение тела m в указанной системе координат, имеет вид

или в проекциях на оси х, у

(2)

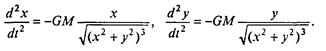
Интересующая нас орбита сильно зависит от «начальной скорости» тела т и «начального расстояния». Мы взяли эти слова в кавычки, так как при изучении движения космических тел нет столь отчетливо выделенного «начального момента», как в ранее рассмотренных ситуациях (тело, брошенное под углом к горизонту). При моделировании нам придется принять некоторое положение условно за начало, а затем изучать движение дальше. Очень часто космические тела движутся практически с постоянной скоростью по орбитам, близким к круговым. Для таких орбит легко найти элементарное соотношение между скоростью и радиусом. В этом случае сила тяготения выступает в роли центростремительной, а центростремительная сила при постоянной скорости выражается известной из начального курса физики формулой mv 2 /r. Таким образом, имеем

(3)

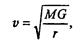
Период движения по такой орбите

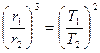
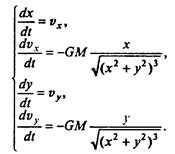
Заметим, что отсюда вытекает один из законов Кеплера, приведший Ньютона к открытию закона всемирного тяготения: отношение кубов радиусов орбит любых двух планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца, т.е. . Более точная формулировка дана ниже (так как реально орбиты планет не вполне круговые). Если соотношение (3) нарушено, то орбита не будет круговой. Выяснить, какой она будет, можно в ходе численного моделирования. Сведем (2) к системе четырех дифференциальных уравнений первого порядка:

(4)

В этой задаче особенно неудобно работать с размерными величинами, измеряемыми миллиардами километров, секунд и т.д. В качестве величин для обезразмеривания удобно принять характерное расстояние от Земли до Солнца ρ = 1,496∙10 11 м, (так называемая, астрономическая единица), период круговой орбиты 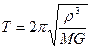,соответствующий этому расстоянию, скорость движения по ней , т.е. принять

После обезразмеривания получаем

(5)

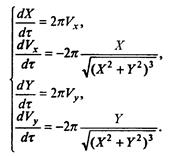
Отметим замечательное обстоятельство: в безразмерных переменных уравнения вообще не содержат параметров! Единственное, что отличает разные режимы движения друг от друга — начальные условия.

Можно доказать, что возможные траектории движения, описываемые уравнениями (5) — эллипс, парабола и гипербола.

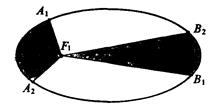
Рис. Иллюстрация второго закона Кеплера

Напомним законы Кеплера, см. рис.

1. Всякая планета движется по эллиптической орбите с общим фокусом, в котором находится Солнце.

2. Каждая планета движется так, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади; на рисунке промежутки времени движения от A₁ к A₂ и от B₁ к B₂ считаются одинаковыми, а площади секторов F₁A₁А₂ и F₁B₁B₂ равны. Это означает, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите.

3. Отношение кубов больших полуосей орбит двух любых планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца.

Уравнения (5) описывают движение не только планет, но и любых тел, попадающих в поле тяготения большой масcы. Так, в Солнечной системе существует огромное количество комет, движущихся по чрезвычайно вытянутым эллиптическим орбитам с периодами от нескольких земных лет до нескольких миллионов земных лет. Судьбы небесных тел, не являющихся постоянными членами Солнечной системы, а залетевших в нее издалека, определяютсяих скоростью—еслионадостаточно велика, то орбита будет гиперболической, и. облетев Солнце, тело покинет Солнечную систему, если нет — перейдет на эллиптическую орбиту и станет частью системы; пограничная между ними орбита — параболическая.

Все эти утверждения можно проверить и детально исследовать с помощью уравнений (5). При этом полезно и удобно использовать одно важнейшее свойство обсуждаемой системы, которого не было у рассмотренных ранее — сохранение полной энергии движущегося тела (такое свойство называется «консервативность»). Полная энергия движущегося небесного тела т в системе двух тел имеет значение

Первое слагаемое — кинетическая, второе — потенциальная энергия. В безразмерных переменных

Наличие неизменного параметра е в ситуации, когда изменяются V_x, V_y, X, Y, позволяет контролировать процесс решения системы дифференциальных уравнений, проверять устойчивость метода, подбирать шаг интегрирования.

Уравнение Кеплера

Статьи по небесной механике пользуются на Хабре некоторой популярностью, поэтому я решил рассказать
об одном фундаментальном уравнении движения, а именно, уравнении Кеплера.
Как известно, финитное движение небесных тел в Солнечной системе происходит по эллипсу. Однако, если необходимо
установить, в какой точке небесное тело находится в заданный момент времени, этой информации недостаточно и надо воспользоваться уравнением Кеплера.

Выведем это уравнение.
Напомню, что эллипс — это сплюснутая на величину

окружность. Здесь e — эксцентриситет.

Площадь эллипса равна

где a — большая полуось.
Согласно второму закону Кеплера, который гласит, что площадь, заметаемая радиус-вектором небесного тела пропорциональна времени, можно написать

где T — период обращения, t — текущее время, t0 — момент времени прохождения перигелия (ближайшей к Солнцу точки орбиты).

Найдем теперь зависимость этой площади от положения небесного тела на орбите, то есть от величины радиус-вектора r и истинной аномалии — угла между перигелием и небесным телом, если смотреть с Солнца.

Для этого введем дополнительную переменную — эксцентрическую аномалию E.
Направим ось x от Солнца (начала координат), которое находится в одном из фокусов эллипса, в сторону перигелия по линии апсид (прямой, соединяющей перицентр с апоцентром).
Создадим также вспомогательную окружность с радиусом, равным большой полуоси эллипса.

Абсцисса небесного тела в точке P будет равна

ордината будет, соответственно, равна

Таким образом, получаем

Для вычисления площади S рассмотрим вспомогательные фигуры:
сектор окружности P’-O-Per:

Сектор эллипса P-O-Per:

Отсюда, прощадь S равна:

Сравнивая это выражение с выведенным ранее из второго закона Кеплера,
получаем:

где M(t)=2*pi*(t — t0) / T

Это и есть уравнение Кеплера.

Заметим, что это трансцендентное уравнение относительно E и получить явное решение в общем случае не удается.

Для вычисления координат небесного тела необходимо найти эксцентрическую аномалию по известному M и e, a затем определить радиус-вектор и угол и, если необходимо x и y по приведенным выше формулам.

Интересным вопросом остается нахождение методов решения уравнения Кеплера.
Этим занимались лучшие умы человечества на протяжении последних четырехсот лет.
Результатом было обогащение математики множеством интересных идей, но описание этого требует отдельной статьи.

Небесная механика — один из разделов астрономии (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

tgE(t)= 1-e2(t) sinυ(t) /(cosυ(t)+e(t);

n(t) = μ/a3(t) .

Итак, по векторам r(t) и r`(t) с помощью формул (35.3) мы получили шесть оскулирующих элементов орбиты: .

На рис. 35.1 показаны оскулирующие орбиты, соответствующие векторам r(t) и r`(t).

Оскулирующие (эллипсоидальные) орбиты должны удовлетворять трем условиям:

1)проходить через точку m, в которой в данный момент времени t находится спутник;

2)проходить так, чтобы касательная к нему совпадала с вектором скорости r`(t) в этот момент времени t;

3) проходить так, чтобы один из фокусов (эллипса) орбиты располагался в притягивающем центре — точке О.

Если такие оскулирующие (эллипсы) орбиты строить непрерывно вдоль возмущенной траектории спутника, то мы получим семейство оскулирующих орбит (рис. 35.1). в результате возмущенная траектория будет являться огибающей (кривой) семейства оскулирующих орбит.

Определение оскулирующей орбиты

Оскулирующая орбита – это мгновенное (виртуальное) коническое сечение, которое определяется вектором положения и вектором скорости спутника, находящегося на возмущенной траектории, в момент времени t (на основании формул (35.2)).

Таким образом, оскулирующая орбита может считаться постоянной в пределах ограниченного отрезка времени в зависимости от заданной точности расчета траектории (рис. 35.2).

Рисунок 35.2 – Пределы применимости оскулирующей орбиты на момент t0 на интервале [t0-Δ; t0+Δ] при заданной погрешности расчета возмущающей траектории.

Тема 16. Интеграл Лапласа.

Продолжаем интегрировать движение спутника

Приведем к виду, удобному для получения еще одного интеграла, независимого от первых двух: интеграл площадей и интеграл энергии.

Для этого умножим равенство (16.1) на векторную константу площадей с первое слагаемое в (16.1) и на r x r´ — второе слагаемое, так как

Преобразуем второе слагаемое в (16.3), где имеется, так называемое двойное векторное слагаемое, которое раскрывается по правилу: «БАЦ – ЦАБ».

Применяя (16.5) к (16.3), находим

Подставляя (16.4) к (16.6)

В равенство (16.3), получаем

Где — λ — произвольная векторная константа которая взята специально со знаком «-»,для того чтобы вектор λ был направлен как будет показано ниже, в ближайшую точку орбит.

И так выражение

где rº = r / r — орт носит название в небесной механике интеграла Лапласа.

Произвольная постоянно может быть определена как обычно, по начальным условиям движения

Так как интеграл Лапласа справедлив для любого момента времени то он справедлив и для начального t0. По этому

Для выяснения физического смысла λ необходимо преобразование (16.8).

Тема №17 Физический смысл вектора Лапласа

17.1 Уравнение орбит полярных координатах.

Мы получили три интеграла:

-энергии h = v² — 2μ/r (17.3)

Наша цель: получить явные выражения для векторов положение r и вектора скорости r´в виде функции времени t и НУ r0, r´0 в t0. Чтобы достичь конечной цели нужно выяснить физический смысл константы (переменной) интегрирования с, h,. Первые две константы с, h: для них установлен физический смысл. Установим физический смысл константы λ. Для этого умножим сколярно интеграл Лапласа (17.4) на текущий радиус-вектор спутника r.

λ · r = -( c x r´)· r — μ rº· r

λ · r = (r x r´)· с — μ (r · r)/ r

Раскроем левую часть (17.5)

Где угол v = λ,^r — как угол между вектора Лапласа и текущим радиус-вектором спутника r обозначает, как правило, v и называется истиной аномалией спутника.

С учетом (17.7) перепишем (17.5)

λrCosv = с² — μr (17.8)

Разрешая уравнение (17.8) относительно r, получаем

r = (17.9)

Обычно (17.9) записывают так (учитывая то что μ ≠ 0)

r = (17.10) — уравнение орбиты в полярных константах r и v.

Чтобы установить физический смысл вектора Лапласа λ нужно сопоставить уравнение (17.10) с уравнением конического сечения в полярных координатах, при этом полярные константы нужно выбрать особым образом.

17.2 . Конические сечения.

Всякая кривая второго порядка есть коническое сечение.

К кривым второго порядка относят:

— вырожденный случай — прямая.

Конические сечения получаются как результат. Сечение поверхности конуса (прямого, кругового) плоскостью. Если плоскость пересечет конус ортогонально оси симметрии конуса, то в сечении получится окружность (рис. 17.1). Если плоскость пересечет конус параллельно образующей линии конуса в сечение парабола (рис. 17.2). Если плоскость пересекает конус параллельно оси симметрии конуса в сечение гипербола.

Если плоскость проходит через вершину конуса и параллельна образующей прямая линия как касательная конуса. Если плоскость пересечет не параллельно и не перпендикулярно оси симметрии эллипс.

π

L

π

Рис.17.1 π || H, то L – окружность Рис.17.5 π перпендикулярна Н, то L – эллипс

π π

Q

L

Рис.17.2 Если π||Q, то L – парабола Рис.17.3 Если π || H, то L — гипербола

От выбора, то есть от выбора расположения начало координат О и выбора ориентировки осей координат, а так же выбора вида координат (прямоугольных, полярных) зависит вид уравнений конических сечений. Например, если выбрать начало координат О в центре симметрии кривой ориентировать оси прямоугольника С координат по оси симметрии кривой, то получается, так называемое коническое уравнение второго порядка.

x²/a² + y²/b² = ± 1 (17.11), где +1 – уравнение эллипса а и b; y

m

π y

L x x

O Рис.17.6 эллипс в Oxyz с полуосями

Рис.17.4 если π проходит через О и касается образующей, L – прямая (два луча)

Если вместо двух переменных x и y выбрать один, так называемый лонгальный параметр Е, то уравнение (17.11) перепишем в виде двух параметрических уравнений.

x = aCosE, y = bSinE (17.12)

Если же переместить начало координат О из центра симметрии эллипса в один из его фокусов (F1 или F2) и заменить вид координат – вместо прямоугольных x и y, взять полярные координаты ρ и φ, то уравнение (17.11) перепишем так (рис. 17.7)

ρ = p / 1 + εCosφ (17.13)

y

m2

m

b O ρ р

F2 F1 x

a

Рис.17.7 Эллипс в полярных координатах

Расстояние между фокусами эллипса F1 и F2

F1 F2 = 2aε (17.14)

и называется фокальным расстоянием. В формуле (17.13) — это половина хорды, проходит через один из фокусов кривой (F1 или F2) перпендикулярно оси симметрии (или точнее, большой полуоси эллипса а) на рис. 17.7 p = F1 Q и p ┴ а. Он связан с большей полуосью формулой

ε = (a² – b²) / a² (17.16)

(17.16) – эксцентриситет эллипса. Теперь сопоставляя уравнения кривой второго порядка (из аналитической геометрии) (17.13) с уравнением (17.10), заключаем, что

r ρ, v φ

c²/μ p, λ/μ ε (17.17)

Уравнение (17.10) – уравнение конического сечения в полярных координатах r и v с полюсом в центре масс центрального тела, (так как исходное уравнение γ мы интегрируем в инерциальную систему координат r´ + (μ/r²)rº = 0)

Являющегося одним из фокусов (F1 или F2) конического сечения. Далее фокальный параметр орбиты p равен

и является одной из констант интегрирования эксцентриситета орбиты

ε ≡ e = λ/μ (17.19),( в небесной механике эксцентриситет обычно обозначают «е» ).

Из того, что v => φ, выясняется направления вектора Лапласа – вектор λ направлен по оси симметрии эллипса в ближайшую точку орбиты π (рис. 17.8)

b P r m

F полюс полярной СК

ae

Рис.17.8 Центр орбины в полярной СК

r = p/ 1+eCosv (17.20) ≡ (17.10) – уравнение орбиты в полярных координатах.

Из сопоставления выражения, получается как следствие интеграла Лапласа,

r = (17.10)

с каноническим выражением конических сечений

ρ = p / 1 + εCosφ (17.13)

следует, что равенство (17.10) представляет собой уравнение конического сечения (окружность, эллипсоид, парабола, гипербола) и переписывается окончательно в виде

r = p/ 1+eCosv (17.20),

р = c²/μ, ε ≡ e = λ/μ, v = μ, е > 1, то орбита — гипербола.

Всякий вектор в трехмерном пространстве должен характеризовать три параметра. Мы установили только для вектора Лапласа, нужно установить физический смысл для направления вектора Лапласа. Таким образом, два оставшихся параметра в векторе λ характеризует его направление в пространстве, которое определяется осью симметрии конического сечения и ближайшей точки орбиты фокуса.

Тема 18. Точки и линии орбиты спутника.

С помощью интеграла площадей мы установили, что орбита спутника – плоскостная кривая, лежащая в плоскости, лежащая в инерциальной системе координат. Эта кривая: замкнутая или разомкнутая и представляет собой одно из конических сечений. Это коническое сечение постоянной орбиты ориентирования внутри орбитальной плоскости. (рис. 18.1 )

P

b m(t)

α O´ v λ

ω π

линия узлов орбиты

Рис.18.1. Точки и линии эллиптической орбиты.

На рис. 18.1 О’ – центр симметрии конического сечения

F1 и F2 – фокусы симметрии конического сечения

π – перицентр орбиты

α – апоцентр орбиты

Оπ — линия апсид орбиты

ОΩ — линии узлов орбиты

Угол v — истинная аномалия спутника

Угол ω — аргумент широты орбиты

ω = π + ωгл, если f 0.

Тема 19. Связь константы площадей энергии спутника h с большой полуосью орбиты a.

Для установления связи h и a воспользуемся интегралом энергии.

Так как интеграл энергии справедлив для любой точки орбиты, вычислим его в точке перицентра орбиты π.(рис19.1)

Vπ

Ω´

v λ

Но из уравнения орбиты

r = p/ 1+eCosv (17.20), получаем

vπ = 0º, rπ = p / (1 + e) = a (1 — e²)/1 +e = a (1 — e)(1 + e)/1 + e = a (1 — e)

rπ = a (1 — e), rα = a (1 + e) (19.3)

Вычислим линейную скорость спутника V в точке π, как произведение угловой скорости радиуса – вектора спутника r. Относительно фокуса О — это υπ на длину вектора r, то есть

Угловую скорость υ получим из полярной формы интеграла площадей

Но из рисунка 18.1 имеем

Дифференцируя (19.6) и учитывая, что ω – константа, получаем, что u´≡ v´ (19.7)

Тогда интеграл площадей, записывают

Сравнивая (19.8) и (19.4) получаем, что

Учитывая, что c = μp

Получаем, что Vπ = μp / 2π = μa(1 — e²) / a(1 — e) (19.10)

После алгебраического преобразования получаем

h = — μ/a (19.11) – установлена связь константы с большой полуосью.

Тема№20. Период обращения спутника. Третий закон Кеплера.

В невозмущенном движении период обращения спутника имеет смысл только для замкнутых орбит (эллипс, окружность). Периодом обращения называется промежуток времени между двумя последовательными прохождениями спутника через одну и ту же (любую) точку орбиты.

Рис.20.1 период обращения спутника.

На рис.20.1 точка О – центральное тело

точка m — любая точка орбиты, через которую проходит спутник дважды в моменты

где T – период обращения

Установим связь Т с большой полуосью орбиты а. Для этого дважды вычислим S эллипса орбиты, один раз из геометрических соображений, другой раз из динамических соображений.

Из аналитической геодезии.

Рис. 20.2 Площадь орбитального эллипса из геометрии

S прямоугольника = 4аb

S эллипса =π ab ( 20.3)

Вычислим из динамических соображений, воспользовавшись вторым законом Кеплера, но в современной формулировке.

Где S´ – скорость изменения площади (секториальная скорость) движения спутника на орбите,

C — константа площадей

Возьмем интеграл по t от выражения (20.4)

∫ S´dt = S орбитального эллипса из динамики (20.6)

∫ ½ С dt = ½ С ( t + T – t ) = ½ μр T (20.7)

Таким образом, S эллипса из динамики = T (20.8)

Поскольку площади S эллипса из геометрии должна быть равна площади из динамики S эллипса из динамики то, приравнивая (20.3) и (20.8), получаем

p = a ( 1 – e2 ), b = a 1 – e2

T = 2πab / μр = 2πa а 1 – e2 / μ а ( 1 – e2 ) = 2π / μ/а3

Формула (20.9) связывает через константы π и μ, период обращения спутника T с большой полуосью его орбиты а. Отсюда следует, что параметр T определяем размер орбиты (полуось а), но большая полуось связана с константой энергии h по формуле.

Но mh/2 — полная энергия спутника, следовательно период обращения спутника T связан с полной энергией спутника и является одной из констант интегрирования дифференциального уравнения движения спутника.

Среднее движение спутника.

Выясним физический смысл знаменателя в формуле

Из (20.9) имеем μ/а3 = 2π / Т (20.11)

Но 2π — полный угол, который описывает радиус-вектор r за время T (период).

Следовательно величина μ/а3 есть средняя угловая скорость движения спутника по орбите. В небесной механике используется термин — среднее движение спутника обозначается «n»

Тогда формула (20.11) переписывается так

n = 2π / Т или Т = 2π / n (20.13)

Из формул (20.11, 20.12) или (20.9) следует третий закон Кеплера в современной формулировке

Из (20.14) следует третий закон Кеплера: «произведение квадрата среднего движения спутника на куб большой полуоси его орбит есть величина постоянная ».

Получим выражение с помощью (20.14) из которой следует формулировка третьего закона (Кеплера) (рис.20.3)

Рассмотрим одно центровое тело O, вокруг которого движение нескольких спутников

( проекция солнечной системы )

Рис. 20.3 Третий закон Кеплера в классической формулировке

Применим (20,14) к системе спутников m1, m2,….,

n12a13= n22a23= n32a33=…=μ (20.15)

Для двух спутников m1 и m2, получаем отношение

n12/ n22 = a23/ a13 (20.16)

Из формулы (20.17) следует третий закон Кеплера в классической формулировке ; «квадраты периодов обращения двух спутников относительно одного и того же центрального тела как

кубы больших полуосей их орбит».

Заменим в (20.16) средние движение n периодом T

(2π / Т1)2 a23 Т12 a23

(2π / Т2)2 a13 Т22 a13

Кеплер установил этот закон эмпирическим путем по Тиха Браги. Мы получили этот закон как частный случай трех законов Ньютона.

Тема№21. Связь трех констант интегрирования;

Лапласа, энергии и площадей.

Наша цель показать, что три произведения постоянного интегрирования ДУ движения спутника λ, h и с. Они являются между собой зависимыми величинами. Для этого воспользуемся интегралом Лапласа и площадей.

λ = с x r´ — μrº; c = r x r´ ( 21.1)

Возьмем в квадрат левую и правую части интеграла Лапласа

λ 2 = [ — (с x r´ + μrº)] = (с x r´)2 +2(с x r´)(μr) + μ2 (rº)2 (21.2)

λ 2 = λ 2 – как скалярный квадрат (21.3)

(с x r´)2 = │ с x r´│2 = │сv Sin (с^v)│2 = (сv)2 (21.4)

r ≡ v – двоякое обозначение вектора скорости

2(с x r´)(μrº) = 2μ (с x r´)rº = 2μ (с x r´) r/r = 2μ/ r (с x r´) r =

= 2μ/ r (r´ x r) с = 2μ/ r (- с2) = — 2μс2/ r

2(с x r´)(μrº) = — 2μс2/ r (21.5)

λ 2 = μ2 + с2h (21.6)

ТЕМА №22. Радиальная трансверсальная составляющие скорости движения спутника.

Скорость движения спутника всегда направлена по касательной к его орбите. Этот вектор скорости раскладывается на две ортогональных составляющих: радиальную и трансверсальную, рис.22.1

Рис.22.1. Радиальная и трансверсальная скорость движения спутника.

На рисунке 22.1 показана орбитальная дуга, притягивает центр О, перицентр π, вектор Лапласа λ, текущее положение спутника m в t, его радиус-вектор r и вектор скорости v, касательный к орбите в точке m.

Vr — вектор радиальной скорости спутника;

Vτ — вектор трансверсальной скорости спутника;

rº — орт радиального направления (он же орт радиус-вектора спутника )

τº — орт трансвкрсального направления

Вектор скорости спутника v можно представить разложение по ортам rº и τº, как сумму двух векторов

V = Vr rº+ Vτ τº (22.2)

Из курса физики вектор скорости V есть производная по времени то радиус — вектора r/t.

V = d/ dt (r (t)) = r´(t) (22.3)

Но радиус-вектор r (t) можно представить как произведение его модуля r (t) на орт rº(t).

r (t) = r (t) • rº(t) (22.4)

Берем производную от равенства (22.4) получаем

V = d/ dt (r (t) rº(t)) = d/ dt [r (t)] rº(t) + r (t) d/ dt[rº(t)] (22.5)

d/ dt (r (t)) = r´ (22.6)

Из курса физики производная от любого вектора r, вращающегося с угловой скоростью ω вокруг оси, проходящей через начало вектора r в направлении ωº, равна векторному произведению r, рис. 22.2 .

d/ dt (r) = ω x r (22.7)

Рис.22.2 Представление линейной скорости.

V = d/ dt (r) = ω x r (22.7)

Применим формулу (22.7´) для вычисления производной и d/ dt (rº (t)), рис.22.3.

Орт rº вращается с угловой скоростью υ´ — скорость изменения истинной аномалии со временем, от сюда следует, что υ´ ≡ ω – модуль угловой скорости (22.7´).

Орт оси вращения вектора rº есть орт сº – векторной константы площадей с.

тогда r´º = ω x rº (22.9)

или r´º = υ´сº x rº

или r´º = υ´ τº (22.10),

где τº = сº x rº (22.11).

Перепишем (22.5) с учетом (22.10)

V = Vr rº + rυ´ τº (22.12)

Сравнивая (22.12) с (22.2)

V = Vr rº+ Vτ τº (22.2), приравнивая их правые части и приравнивая скалярные множители при одинаковых ортах, получаем

Vr = r´ , Vτ = r υ´ (22.13)

Из формул (22.13) следует, что радиальная составляющая скорости отвечает за изменение длины радиуса – вектора спутника, а трансверсальная составляющая – отвечает за линейную скорость и движения спутника по виртуальной окружности радиуса r. Установим связь радиальной Vr и трансверсальной Vτ скорости спутника с параметрами орбиты: р — фокальный параметр орбиты, е – эксцентриситетом орбиты и углом υ– истинной аномалии силы.

Для этого воспользуемся двумя интегралами:

— уравнением орбиты в полярных координатах

r = p/ 1+eCosυ (22.14),

— интегралом площадей в полярных координатах

c = r²υ´, c = μp (22.15)

Дифференцируя (22.14) по t, получаем

Vr = r´ = p(e+Sinυ)υ´ p = μp eSinυ = μ / p eSinυ

Итак, Vr = μ / p eSinυ (22.16)

Для получения трансверсальной скорости Vτ как функции р, е и υ сравнивают два выражения (22.13) с (22.15)

c = r²υ´ Vτ = с/r (22.17)

Или с учетом (22.14) и (22.15), находим

Vτ = μ / p (1+eCosυ) (22.18)

Формулы (22.16) и (22.18) устанавливаем связь Vr и Vτ с направлением орбиты р, е и υ. Полезны формулы, связи скорости:

V = 2μ / r + h (22.20) — интеграл энергии.

ТЕМА №23. Эксцентрическая аномалия (геометрическая интерпретация) спутника.

Для определения положения спутника на заданной орбите в небесной механике используется три аномалии:

Истинная была введена в разделе уравнения орбиты нормальных координат. Она отслеживает истинный угол вращения спутника рис.23.1.

Рис. 23.1 Истинная аномалия

Истинная аномалия более сложным образом связана со временем t. Эксцентрическая аномалия Е связана со временем Е(t) более простой формулой, чем υ(t).

Средняя аномалия М связана со временем наиболее просто по линейному закону.

Все три аномалии связаны между собой.

υ ( E ( M (t))) = υ (t) (23.1)

Покажем на рис.23.2 геометрическую интерпретацию эксцентрической аномалии.

Рис. 23.2 Эксцентрическая аномаоия

На рис.23.2 О’ – центр симметрии орбитального эллипса, О – притягивающий центр

( центральное тело ), m – положение спутника на орбите в текущий момент времени, вектор qm перпендикулярен линии апсид Оπ,

угол πОm = υ – истинная аномалия спутника, которая отслеживает истинный угол υ поворота радиус – вектора спутника r относительно вектора Лапласа λ ( или линии апсид ), угол πО’m’ = Е – эксцентрическая аномалия спутника, вершина угла Е находится не в центре масс тела, а в центре симметрии орбитального эллипса, точка m’ – виртуальная точка движения по окружности радиуса в центре с центром симметрии эллипса и получается как результат пересечения перпендикулярно вектору qm с окружностью.

Из рис.23.2 видно, что две точки m и m’ при движении спутника m по орбите сливаются в одну точку в двух случаях:

1. когда спутник находится в перицентре π,

2. когда спутник находится в апоцентре α.

Правильное применение терминов перицентр ( перигей ), апоцентр ( апогей ) и т. п.

Когда центральное тело безымянное или же обсуждается задача двух без относительно какого либо центрального тела, то точки орбиты π и α называется перицентром и апоцентром. Если же уентральное тело имеет имя, или решение конкретной реальной задачи двух тел, то название точек меняется ( см. в таблице ).

центральное тело перицентр апоцентр

Земля( спутник: Луна, иск. Спутник ) перигей апогей

Солнце ( спутник 6 Земля, Венере и т. д. ) перигелий афелий

Луна ( иск. спутник ) переселений апоселений

Тема№24. Эксцентрическая аномалия спутника. Аналитическая связь двух аномалий.

Для получения формулы выражающие эксцентриситет аномалии через истинную или наоборот введем три орбитальных системы координат. Орбитальная система — основная плоскость совпадает с плоскостью орбиты.

1. Система координат Oξη с началом притягивающим центре О и осью Oξ абсцисс, направленный по линии апсид Oπ.

α m линия апсид полярная ось

Рис. 24.1 Связь истинной и эксцентрической аномалии.

2.Полярная система координат с полюсом в точке О и полярной осью направлена по линии апсид с полярными координатами r и υ.

r – полярное расстояние

υ – полярный угол

( в небесной механике r – модуль радиус-вектора спутника, υ – истинная аномалия спутника)

3. Прямоугольная система координат О´xy с началом O´ в центре симметрии орбиты и осью абсцисс O´y направленной по линии апсид. Уравнение орбиты спутника в системе координат О´xy имеет вид (см. аналитический геометрический метод ).

Уравнение орбиты спутника в полярной системе координат ( r,υ) имеет вид

r = p/ 1+ eCosυ (24.2)

где p = a(1-e²), e² = a² – b² / a² , b = a 1 — e² (24.3)

ae = О´О– полуфокальное расстояние

Уравнение орбиты спутника в параметрической форме

Уравнение дано без выводов, где Е — параметр. Если подставить (24.4) в (24.1),то получим тождество, что свидетельствует о правомерности введение уравнения (24.4).уравнение орбиты в координатах ξ и η (из рис. 24.1)

ξ = rCosυ, η = rSinυ (24.5)

С другой стороны, с центром (24.4) и рис.24.1 получаем

ξ = x – ae = aCosE – ae = a(CosE – e)

η = y = bSinE = a 1 — e² Sin E

y = a 1 — e² Sin E (24.6)

Сопоставляя (24.6) и(24.5), находим искомую связь

rCosυ = a(CosE — e)

rSinυ = a 1 — e² Sin E (24.7)

Заменим r с помощью формулы

r = a(1 — eCosE) (24.8),

которая получается из рис.24.1 по теореме Пифагора

r² = ξ² + η² = [a(CosE – e)]² + (a 1 — e² Sin E )²

Подставляя (24.8) в (24.7), получаем окончательно –

Cosυ = CosE – e / 1 – eCosE (24.9)

Sinυ = 1 — e² Sin E / 1 – eCosE (24.9)

Формулы (24.9) устанавливают связь Е и υ в одну сторону: Е => υ. Получим обратную связь:

υ =>Е. Можно воспользоваться формулой для тангенса половинного угла

tg α/2 = 1 – Cosα/ 1 + Cosα (24.10)

Заменим в (24.10) α на υ

tg υ/2 = 1 – Cosυ/ 1 + Cosυ (24.11)

Подставив в (24.11) равенство (24.9), получим окончательно

tg υ/2 = 1 + e / 1 – e tg E/2 (24.12)

tgE/2 = 1 + e / 1 – e tg υ/2 (24.13),

формулы (24.9),(24.12),(24.13) устанавливают связь Е υ.

Тема№25. Уравнение Кеплера.

Уравнение Кеплера — последний четвертый независимый интеграл решаемого дифференциального уравнения.

Уравнение устанавливает связь угла поворота равенств со временем t. Для получения этой связи воспользуемся интегралом площадей в полярной форме

Где υ´=dυ/dt — скорость измерения истинной аномалией υ со временем t.

Из (25.2) получаем интеграл r²•dυ/dt = c или разделяя переменные υ и t, так чтобы они находились в различных частях равенства.

и интегрируя t(υ)

Интеграл (25.4) сложен

∫ a(1 — e²) /1 + eCosυ dυ = ?

Необходимо привести его к табличному виду

r = a ( 1 – eCosE ) (25.5)

Остается найти dυ через dE.

Для этого воспользуемся формулой

Cosυ = CosE – e / 1 – eCosE (25.6)

Дифференцируя по υ левую часть и по Е правую, находим

-SinEdE (1 – eCosE) – (CosE – e)(eSinE)

Завершить самостоятельно; используем для Sinυ формулу (24.9)

Итог: dυ = 1 — e² dE / 1 — eCosE (25.7)

Подставляя (25.7), (25.5) в (25.4), получаем

∫ a²(1 — eCosE)² 1 — e² / 1 – eCosE dE = ∫ cdt

∫ (1 — eCosE) dE = ∫ c / a² 1 — e² dt (25.8)

Выражение (25.8) легко интегрируется.

Интегрируя левую часть (25.8), находим

E – eSinE = E – eSinE (25.9)

Учитывая, что при υ=0, эксцентрическая аномалия Е так же равна нулю.

Интегрируя правую часть (25.9), находим

t = t = (t — tπ) = n (t — tπ) (25.10) a 1 — e² a² 1 — e² a 1 — e²

Из третьего закона Кеплера n²a3 = μ имеем n = μ/а3

Где n — среднее движение спутника,

а — большая полуось орбиты,

μ — гравитационный параметр центрального тела.

Объединяя (25.10) и (25.9) согласно (25.8), находим окончательно, что

E – eSinE = n (t — tπ) (25.11)

Выражение (25.11) носит название в небесной механике – уравнение Кеплера.

Оно связывает эксцентрическую аномалию спутника Е со временем t через три параметра : e, a, tπ — константы.

Уравнение Кеплера – четвертый интеграл r´´ + (μ/r²)rº = 0, для четвертого интеграла достаточно построить траекторию спутника и выразить явно радиус спутника r как функцию времени t: r(t).

Тема№26. Средняя аномалия спутника.

В уравнение Кеплера Е – eSinE = n (t — tπ) (26.1)≡(25.11),

выясним физический смысл правой части n (t — tπ) — ?

Параметр n — есть угловая скорость (средн.) движения спутника по орбите. Тогда произведение n (t — tπ) представляет собой угол, который обозначен через μ.

При текущем времени t, равном tπ, из формулы (26.2) следует, что μ = 0. Отсюда вытекает, что угол μ отсчитывается от точки π — перицентра. Угол μ в небесной механики называется средней аномалией спутника. И этот угол отслеживает движение фиктивной точки по окружности с постоянной угловой скоростью n. (см. рис.26.1). Момент tπ истинная υ и эксцентрическая Е аномалии равны 0. В tπ : υπ = 0, Еπ = 0 и как следует из (26.2), Мπ так же равняется 0. То есть образованные все три аномалии учитываются от одного и того же направления – линии апсид (или, что то же самое от вектора Лапласа ).

В небесной механики вводят понятие средней аномалии спутника в начальную эпоху t0, по формуле, на основе (26.2)

M0 = M(t0) = n (t0 — tπ) (26.3)

Тогда выражение (26.2) для средней аномалии M перепишется так:

M = M0 + n (t – t0) (26.4)

Рис.26.1 три аномалии спутника: υ(t), E(t), M(t).

Подстановкой в (26.4) формулы (26.3) самостоятельно проверить совпадение с формулой (26.2) С учетом введенных обозначений для средней аномалии M уравнение Кеплера (25.11) ≡ (26.1) обычно записывают в виде

E – eSinE = M (26.5) .

Тема№27. Итеративный метод решения уравнения Кеплера.

Уравнение Кеплера M = E – eSinE (27.1) ≡ (26.5)

в одну сторону решается явно (то есть когда дана эксцентрическая аномалия Е и ищется средняя аномалия спутника M, при условии, что эксцентриситет известен). В обратную сторону (то есть когда дано M, а ищется Е то нет в математике способов решения таких нелинейных (трансцендентных уравнений) явно аналитического решения получить не возможно, то есть

M => E — проблема аналитического решения.

Для таких трансцендентных уравнений (когда искомая функция входит под знак тригонометрической функции так и явно) существует множество численных методов, мы рассмотрим один — итерационный способ решения. Этот способ применим только тогда, когда

Итеративная формула имеет вид

Где k = 1, 2…. – порядковый номер итерации

В качестве начального значения Е (0) можно принять любое число, например Е(0) = 0º,или Е(0) =М (в последнем случае на одну итерацию будет меньше).

к = 1 Е(1) = М + e sin Е(0)

k = k E(k) = M + e sin Е(k-1)

продолжая до тех пор пока не выполнится критерии окончания итерации: два последовательных значения эксцентрической аномалии E(k) и Е(k-1) не станут различаться между собой на заданную величину погрешности расчетов ε.

│E(k) — Е(k-1)│≤ ε ( в радианах ).

Тема 28. Связь трёх аномалии спутника v, Е и М со временем t полёта.

Приведем здесь сводку формул, полученных в предыдущих разделах, связывая три аномалии спутника v, Е и М, как между собой, так и со временем t.

tg (v/2) = 1 + e /1 — e tgE/2 (28.1)

tg (Е/2) = 1 + e /1 — e tgυ/2 (28.2)

М = Е – е sin E (28.3)

M = M0 + n(t – t0) (28.5)

С помощью формул (28.7) решается все множество задач связанных с полетом спутника от одной точки орбиты до другой. В этих задачах вычисляется либо время полета между двумя точками либо угол поворота.