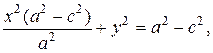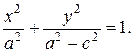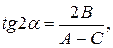Полярное уравнение кривой второго порядка.
Пользуясь общим свойством эллипсов, гипербол и парабол, выведем общее уравнение этих кривых второго порядка в полярных координатах при некотором специальном выборе полярной системы координат.
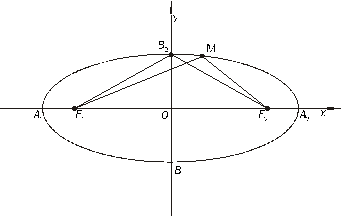
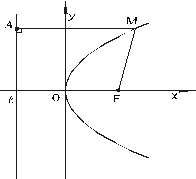
Пусть дана произвольная из указанных линий (эллипс, ветвь гиперболы или парабола). Возьмем фокус F кривой (любой, если их два) и соответствующую ему директрису L (если рассматривается ветвь гиперболы, то берется фокус и директриса, ближайшие к этой ветви).
Введем полярную систему координат так, чтобы полюс О совпал с фокусом F, а полярная ось была направлена по оси симметрии кривой в сторону, противоположную директрисе L.
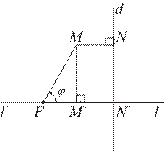
Возьмем на кривой произвольную точку М(r;j), соединим ее отрезком FM с фокусом и опустим перпендикуляр МК на директрису. Кроме того, из точки F проведем перпендикуляр FR к полярной оси до пересечения с кривой в точке R, а из точки R опустим перпендикуляр RQ на директрису (Рис. 12).
 | Обозначим FR через p и будем называть это число фокальным параметром. На основании общего свойства кривых второго порядка  По тем же соображениям: По тем же соображениям:  или или  , откуда , откуда  . . |
Подставим найденные выражения для FM и КМ в равенство 

Уравнение (3) называется уравнением кривой второго порядка в полярных координатах. При e 1 — ветвью гипиерболы, при e=1 — параболой.
Фокальный параметр Р из уравнения параболы определяется непосредственно. Для того, чтобы фокальный параметр выразить через параметры эллипса и гиперболы, следует заметить, что фокальный параметр Р является ординатой точки кривой, абсцисса которой равна абсциссе соответствующего фокуса (в выбранной при выведении канонического уравнения соответствующей кривой системе ХОY).
Подставляя вместо координат точки М(х;у) в уравнение эллипса 



Аналогично, подставляя в уравнение гиперболы координаты точки (с;р), получим:


откуда следует соотношение

Рассмотрим несколько задач на кривые второго порядка.
Задача 1.
Дано уравнение гиперболы 16х 2 -9у 2 =144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы.
Решение.
Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:


откуда а=3, b=4, 

Действительная ось 2а=6; мнимая ось 2b=8.
Уравнения директрис: 
Уравнения асимптот: 
Задача 2.
Составить уравнение эллипса, симметричного относительно координатных осей, зная, что он проходит через точки М1(2;3) и М2 
Решение.
Учитывая симметричность эллипса относительно осей координат, его каноническое уравнение будет иметь вид: 
определим параметры эллипса а и b.


получим следующую систему уравнений:

Решая ее, получим, что:

откуда а 2 =16, b 2 =12.
Следовательно, искомое уравнение эллипса будет:

Задача 3.
Найти вершину, фокус, ось и директрису параболы
Решение.
Преобразуем данное уравнение следующим образом:
Отсюда 
Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы

Отсюда 

xF = xO` = 4; 
то есть F 

Задача 4.
Уравнение эллипса 

Решение:
Найдем из данного уравнения параметры a, b, c, затем найдем эксцентриситет 

а 2 =4, b 2 =3, c 2 =1, 

Искомое уравнение будет иметь вид:



Задача 5.
Дано уравнение кривой в полярных координатах

Привести его к каноническому уравнению в прямоугольных координатах.
Решение.
В данном уравнении 

Из этой системы находим, что а=1, с=3, b 2 =8. Следовательно, уравнение гиперболы имеет вид:

Полярные уравнения кривых второго порядка
Пусть кривая g — это эллипс, гипербола или парабола, точка F — фокус кривой g, прямая d — соответствующая этому фокусу директриса, e — эксцентриситет кривой g.. Как было доказано в § 37 : M Î g Û 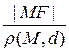
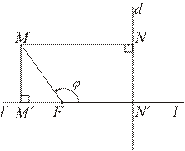
Введем полярную систему координат (r,j) так, чтобы точка F была полюсом, а полярная ось l была бы перпендикулярна директрисе d, и кривая g лежала бы с фокусом F по одну сторону от прямой d.
Пусть M(r,j) — точка плоскости такая, что M ≠ F и M Ï d.
Пусть l’ — прямая, содержащая ось l,
точка N — основание перпендикуляра из точки M на прямую d (MN ^ d, N Î d),
точка M’ — основание перпендикуляра из точки M на прямую l’ (MM’ ^ l’, M’ Î l’),
точка N’ — точка пересечения прямых l’ и d.
1 случай. j £ 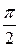
Из треугольника FMM’: |FM’| = r cosj.
|M’N’| = |FN’| + |FM| = |FN’| + r cosj
2 случай.

Так как |MN| = p + r cosj, то мы получаем: 
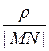
Итак, мы доказали следующую теорему:
Теорема. Эллипс, гипербола или парабола может быть задана в полярной системе координат уравнением вида r = 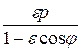
Замечание.
В качестве параметра p иногда фокусируют другую величину, а именно |FF’|, где F’ Î g и FF’ ^ l’. Можно показать, что |FF’| = ep, так что для параболы полярное уравнение с таким параметром будет таким же, а для эллипса и гиперболы примет вид: r = 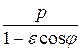
Упражнения.
1) Исследуйте, какие значения может принимать j в уравнении кривой второго порядка (Указание. Отдельно рассмотрите уравнения эллипса, гиперболы, параболы).
2) Выведите формулу для вычисления параметра p по каноническому уравнению кривой второго порядка.
Поверхности второго порядка
Классификация поверхностей второго порядка
Определение. Поверхностью второго порядка в пространстве будем называть множество точек, которое в некоторой декартовой системе координат может быть задано алгебраическим уравнением второго порядка, то есть уравнением вида
Лемма (о корректности определения).
Понятие поверхности второго порядка не зависит от выбора декартовой системы координат, то есть если некоторое множество задается алгебраическим уравнением второго порядка в некоторой декартовой системе координат, то и в любой другой декартовой системе координат это множество задается алгебраическим уравнением второго порядка.
Доказательство.
Аналогично случаю кривых второго порядка
Теорема (о классификации поверхностей второго порядка) (Без доказательства)
Для любой поверхности второго порядка существует декартова система координат такая, что уравнение данной кривой в этой системе будет иметь один из следующих видов (и других поверхностей второго порядка не существует):
| № п.п. | уравнение | название |
 = 1, a > 0, b > 0, c > 0 = 1, a > 0, b > 0, c > 0 | эллипсоид | |
 = 0, a > 0, b > 0, c > 0 = 0, a > 0, b > 0, c > 0 | точка (начало координат O (0, 0 ,0) | |
 = -1, a > 0, b > 0, c > 0 = -1, a > 0, b > 0, c > 0 | Æ | |
 = 1, a > 0, b > 0, c > 0 = 1, a > 0, b > 0, c > 0 | однополостный гиперболоид | |
 = 0, a > 0, b > 0, c > 0 = 0, a > 0, b > 0, c > 0 | конус | |
 = -1, a > 0, b > 0, c > 0 = -1, a > 0, b > 0, c > 0 | двуполостный гиперболоид | |
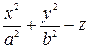 = 0, a > 0, b > 0 = 0, a > 0, b > 0 | эллиптический параболоид | |
 = 0, a > 0, b > 0 = 0, a > 0, b > 0 | гиперболический параболоид | |
 , a > 0, b > 0 , a > 0, b > 0 | эллиптический цилиндр | |
 , a > 0, b > 0 , a > 0, b > 0 | прямая (ось (Oz)) | |
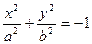 , a > 0, b > 0 , a > 0, b > 0 | Æ | |
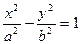 , a > 0, b > 0 , a > 0, b > 0 | гиперболический цилиндр | |
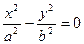 , a > 0, b > 0 , a > 0, b > 0 | две пересекающиеся плоскости ( 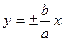 ) ) | |
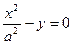 , a > 0 , a > 0 | параболический цилиндр | |
 , a > 0 , a > 0 | две параллельные плоскости ( 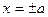 ) ) | |
 , a > 0 , a > 0 | плоскость ( 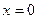 ) ) | |
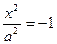 , a > 0 , a > 0 | Æ |
Определение. Уравнения, указанные в таблице теоремы классификации, принято называть каноническими уравнениями поверхностей второго порядка.
Определение. Сечением поверхности второго порядка будем называть пересечение этой поверхности и некоторой плоскости.
Лемма. Любое сечение поверхности второго порядка — это кривая второго порядка.
Доказательство.
1) Рассмотрим сечение поверхности, заданной уравнением (*) плоскостью z = 0.
Ясно, что в плоскости z = 0 мы получим кривую второго порядка, заданную уравнением a11x 2 + 2a12xy + a22y 2 + 2b1x + 2b2y + c = 0.
2) Рассмотрим сечение поверхности второго порядка плоскостью a.
Существует преобразование декартовой системы координат такое, что плоскость a будет задаваться в новой системе координат уравнением z = 0 (то есть плоскость a будет совпадать с плоскостью (Oxy)). Так что сечение поверхности второго порядка плоскостью a будет так же кривой второго порядка.
Замечание. Факт, изложенный в предыдущей лемме, лежит в основе изучения поверхностей второго порядка методом сечений. По тому, какие сечения мы можем получить, можно составить представление о форме поверхности.
Лекция 8. Линии второго порядка.
8.1. Окружность, исследование уравнения окружности.
8.2. Вывод канонического уравнения эллипса.
8.3. Гипербола и парабола, их канонические уравнения.
8.4. Линии второго порядка. Приведение кривых второго порядка к каноническому виду.
8.5. Полярное уравнение кривой второго порядка.
8.1
Окружностьюназывается множество всех точек плоскости, равноудаленных от данной точки (центра окружности) на расстояние, равное радиусу окружности.
Пусть С(а,в) – центр окружности, r – радиус окружности, M(x,y) – произвольная точка окружности (Рисунок 8.1). По определению окружности 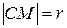
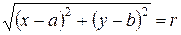
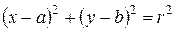
Таким образом, координаты любой точки, лежащей на окружности, удовлетворяют уравнению (8.1). Покажем, что координаты точки, не лежащей на окружности, не удовлетворяют уравнению (8.1).
Действительно, если точка М — внутри окружности, то расстояние 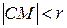
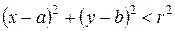
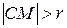
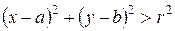
Если в уравнении (8.1) раскрыть скобки, то получим уравнение
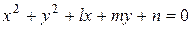
где 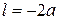
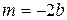
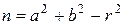
Если 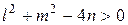
Если 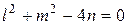
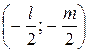
Если 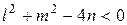
Рисунок 8.2.Окружность, имеющая
Уравнение (8.1) можно упростить, если поместить начало новой системы координат в центр окружности (Рисунок 8.2). Тогда ее уравнение будет иметь вид:
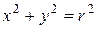
Это уравнение называется каноническим уравнением окружности, т.е. уравнением самого простого вида.
8.2
Эллипсомназывается множество всех точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (ее обозначают 2а) и большая, чем расстояние между фокусами.
Середина расстояния между фокусами называется центром эллипса, т.к. относительно этой точки эллипс симметричен.
Длина |F1F2| называется фокусным расстоянием, обозначим ее 2с, а половина этого расстояния называется полуфокусным расстоянием, оно равно с.
Примем центр эллипса за начало координат, за ось абсцисс примем прямую, проходящую через фокусы (Рисунок 8.3).
Рисунок 8.3. Эллипс
Тогда координаты фокусов будут F1(-c;0), F2(c;0). Всякий отрезок, соединяющий две точки эллипса, если он проходит через центр, называется диаметром эллипса. Наибольший диаметр проходит через фокусы, этот диаметр A1A2 называется большой осью эллипса. Длина большой оси эллипса |A1A2|=2a. Действительно, по определению эллипса |F1A2|+|F2A2|=2a, но |F1A2|=|OA2|+c, |F2A2|=|OA2|-c. Тогда получаем 2|OA2|=2a, или |OA2|=a. Аналогично |A1O|=a, следовательно, |A1A2|=2a. Число а называется большой полуосью. Наименьший диаметр эллипса перпендикулярен наибольшему, его называют малой осью эллипса и обозначают через 2b, так что |B1B2|=2b. Число b называется малой полуосью. Концы осей, т.е. точки A1,A2,B1,B2 называются вершинами эллипса. Основное свойство эллипса применимо и для вершин В1 и В2. Например, для вершины В2 получим |F1B2|+|F2B2|=2a, а т.к. |F1B2|=|F2B2|, то 2|F2B2|=2a, или |F2B2|=a. Тогда из прямоугольного ∆OF2B2 получаем важное соотношение:

Форма эллипса при заданном а зависит только от расстояния между фокусами, т.е. от с. При сближении фокусов и при совпадении их с началом координат эллипс постепенно обратится в окружность. Наоборот, если фокусы отодвигаются от начала координат, эллипс постепенно сплющивается и вырождается в прямолинейный отрезок A1A2. Степень сжатия эллипса определяется его эксцентриситетом, который определяется дробью:
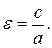
Для эллипса эксцентриситет может изменяться от 0 до 1, причем для окружности 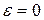

Для получения канонического уравнения эллипса возьмем произвольную точку эллипса М(x,y). Тогда по определению |MF1|+|MF2|=2a. Выразим это равенство в координатах:

Для упрощения уравнения (8.6) придется дважды его возводить в квадрат и приводить подобные члены. В результате будет получено уравнение
или после деления на 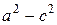
Далее учитывая, что b 2 =a 2 -c 2 , получаем каноническое уравнение эллипса:

Построение эллипса, согласно его определению, можно осуществить посредством нити длиной 2а, закрепленной концами в фокусах. Зацепив нить острием карандаша, и двигая его так, чтобы нить всё время была в натянутом состоянии, мы заставим острие вычертить эллипс.
8.3
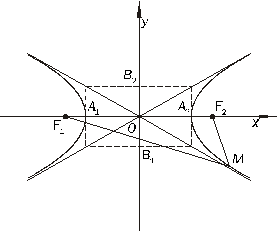
Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек 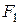
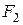
Середина расстояния между фокусами называется центром гиперболы, так как относительно этой точки гипербола симметрична. Длина 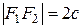
Всякий отрезок, соединяющий две точки гиперболы и проходящий через центр, называется диаметром гиперболы. Наименьший диаметр лежит на оси абсцисс; этот диаметр 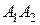
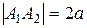

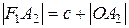

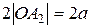
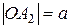
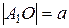
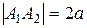
Число 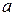
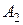
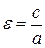
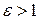
Рисунок 8.4. Гипербола
Пусть 
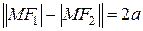
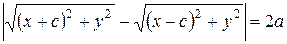
Уравнение (8.8) в результате преобразований, аналогичных проводимым при выводе уравнения эллипса, может быть сведено к виду:
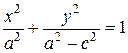
Обозначая 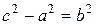
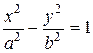
Прямые 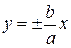
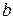
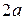
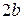
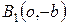
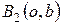
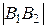
Если в уравнении (8.9) 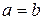

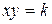
Заметим, что уравнение

тоже определяет гиперболу, у которой действительная ось расположена на оси 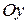
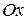
Параболой называется множество всех точек плоскости, равноудаленных от данной точки 
Для вывода канонического уравнения параболы проведем ось 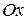

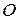
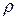
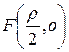
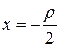

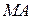
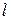
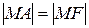
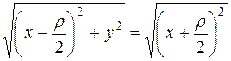
Рисунок 8.5. Парабола.
Возводя в квадрат и приводя подобные, получаем каноническое уравнение параболы:
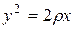
Вершинойпараболы называется точка пересечения параболы с ее осью симметрии. Ось симметрии параболы называется осью параболы. Парабола, определяемая уравнением (8.11), имеет ось, совпадающую с осью 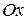
Заметим, что уравнение 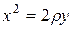
8.4
Между эллипсом, гиперболой и параболой имеется близкое родство. Это объясняется тем, что все они — линии второго порядка. Все эти линии могут быть получены при пересечении прямого кругового конуса с плоскостью, поворачивающейся вокруг оси, выбранной, например, перпендикулярно к оси конуса (Рисунок 8.6). Пока наклон мал, в сечении получается эллипс. При увеличении наклона эллипс удлиняется, его эксцентриситет растет. Когда плоскость наклонена к оси конуса так же, как образующие, в сечении получается парабола. Наконец, когда плоскость будет пересекать обе половины конуса, в сечении будет гипербола. По этой причине эллипс, гиперболу и параболу иногда называют коническими сечениями.
Рисунок 8.6. Родство кривых второго порядка.
Родство между указанными линиями обусловлено тем, что все они задаются уравнением второй степени, а поэтому и носят общее название линий(или кривых) второго порядка.
Общим уравнением линий второго порядканазывается уравнение вида
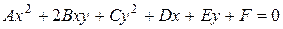
Путем преобразования координат это уравнение можно привести к каноническому виду. Осуществим поворот осей координат на угол 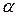
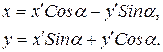
Угол 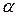
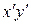
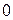
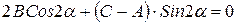
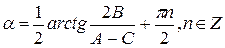
Формула (8.15) определяет 4 возможных значения для 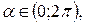
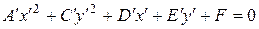
Если 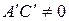

которое с помощью параллельного переноса начала координат
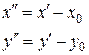
сводится к каноническому виду.
Если 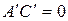

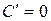
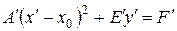
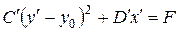
Применяя параллельный перенос (8.18), где 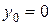
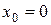
Заметим, что при любом повороте осей координат (8.13), хотя координаты 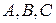
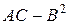
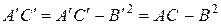
1. Если 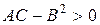
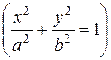
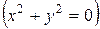
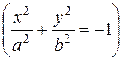
2. Если 
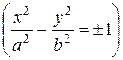
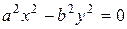
3. Если 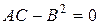
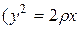
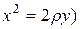
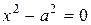
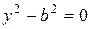
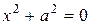
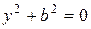
8.5
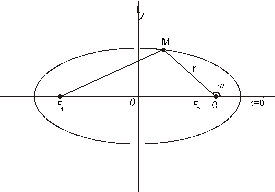
Выведем полярное уравнение линии второго порядка на примере эллипса.
Рисунок 8.7. Полярное уравнение эллипса
Поместим полюс 
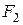

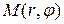
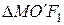

Учитывая, что 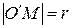
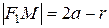
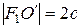

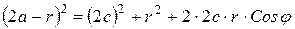
Откуда, заменяя 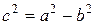
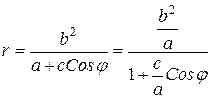
Обозначим 
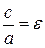
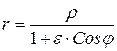
полярное уравнение эллипса.
Если поместить полюс в левый фокус эллипса, то полярное уравнение будет иметь вид
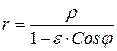
Заметим, что уравнения (8.21) и (8.22) являются полярными уравнениями любой кривой второго порядка, его вид определяется величиной эксцентриситета. Если 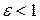
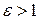
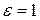
Дата добавления: 2015-08-21 ; просмотров: 2232 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://lektsia.com/4x4ca8.html
http://helpiks.org/4-98295.html