Пользуясь инвариантами упростить уравнение параболы

Упрощение уравнений кривых 2-го порядка

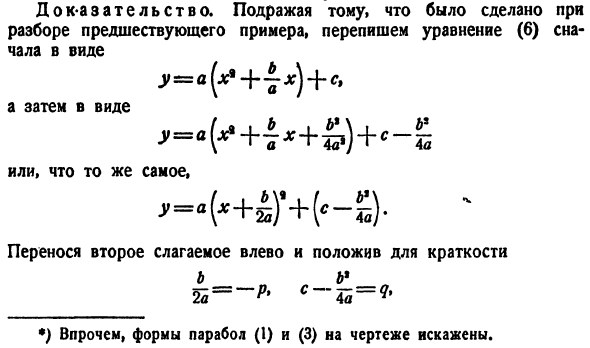
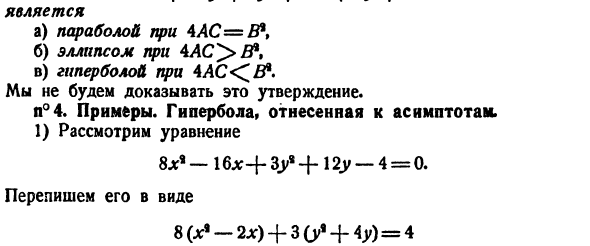
Упрощение уравнений кривых 2-го порядка

• Упрощение уравнения кривой 2-го порядка Н°1.Уравнение y = axh — \ — bx — <- c. в этом разделе описывается применение преобразований координат для упрощения уравнения 2-й строки. Давайте начнем с примера. Предположим, вы хотите найти линию, которая соответствует уравнению. у = 12л:+ 9.(!） объедините члены,

содержащие x, и перепишите это уравнение. вы добавите выражение в скобках с полным квадратом, вы получите: у = 3(х *-4х + 4)+ 9-12 Или то же самое у + 3 = 3(ок-2)’. (2） Это исходное уравнение (1), но только если группа членов отличается. Предположим, что здесь система координат переведена и начало

координат перемещено в точку 0 (p, q).Тогда старые координаты всех точек плоскости (x, y) представляются новыми координатами(xlt бьется по формуле). х = ХВ + р, г = г \ + Людмила Фирмаль

Теорема. соответствует параболе, полученной из параболы у = АХ *(7） Используйте параллельную передачу. Y、\ ыы З 4 * -/ −2 __ N л Дж 0 и C> 0 ( * ).И понятно, что это Λ1> 0.In дело в том, что если M = 0, то выражение (17) не является кривой, а соответствует точке, как в Примере (13), а неравенство 0 приводит к тому, что нет ничего, что соответствует выражению (17), например (12).Поэтому остается только возможность M> 0. Перепишите выражение (17) в следующий

формат •) Понятно, что это Еф 0.В противном случае выражение(11) будет иметь вид Ax * — * — Dx — * + ^ = 0 и будет соответствовать паре строк[подобно выражению(16)]. Рычание (15)]вообще никакого ответа «9 мая внимательно следите за процессом умозаключения. Но учтите, что вы не хотите запоминать выражение ru q, At. Do не загружайте ненужные детали в память. •* * ) В противном случае измените знак

на обеих сторонах уравнения(17). Ич I_1 „LG +“ LG-1 Или,=(это、 Дроби положительные), в виде] ФЛ-П-21-1 * б％ Это эллиптическое уравнение. Необходимо учитывать, когда А и С — это количество различных знаков. В противном случае, поскольку он изменяет знак с обеих сторон выражения (17), мы можем предположить, что O, C 0, C 0.Переписывание формулы (18) из Формулы (17) если вы поставите — = ^ = — b, он достигнет уравнения. О1-б * ’ То есть к гиперболическому уравнению. Теорема доказана. Замечание. 1) метод доказательства теоремы, примененный к определенному уравнению, фактически делает это уравнение каноническим. 2)из доказательства

теоремы ясно, что кривая, соответствующая уравнению*). Ах * + ТИЦ * ’\ — ДХ + ЕУ + Ф = 0、 Что это? а) LS = O парабола、 B) LS] > 0 эллипс、 в) преувеличение препарата (19） Где L обозначает совокупность всех остальных терминов. Понятно, что L не включает в себя 2-й член по отношению к xx. In в частности, L не включает продукт. запишем все члены формулы (19), включая x% Vy, отдельно. [- 2A sin 0 cos 0 + V (cos9 0-sin 90)+2Csin 0 cos 0] и позже 2sin

0 cos 0 = sin 20, cos90-sin9 0 = cos20、 Указанная группа членов может быть записана следующим образом [В COS 20-(л-с) грех 20] Xyyv Наша цель-выбрать такой угол 0, чтобы в Формуле (19) не было членов, содержащих произведение XYY. I cos 20-(Л-С) sin 20 = 0 (Л-с) грех 20 = потому что я 26、 Или наконец-то (21） Поскольку любое вещественное число действует как касательная к углу, всегда будет

существовать угол 0, удовлетворяющий соотношению (21) (для A, B, C).Но это также означает, что с помощью правильного вращения системы координат уравнение(10) всегда можно преобразовать в уравнение, не содержащее произведения координат. Замечание. 1) Если Λ= C, то уравнение (21) теряет свою meaning. In в этом случае он должен быть изменен на равенство (20). cos 20 = 0、 То есть cos 20 =

0 (ведь мы будем считать Bf 0).Однако это 20 = 90°, то есть 6 = 45°. Итак, при A = C нужно повернуть систему координат на 45°). 2) применяя метод доказательства теоремы к конкретному уравнению, мы можем сделать это уравнение каноническим. Однако существуют и более удобные методы для этой цели. Мы не будем

их рассматривать. (20 )） Или то же самое 3) по отношению к уравнению (10) возникают следующие критерии: кривая**) соответствует уравнению Топорик% + Ву + Су *-+ ДХ + ЕС + Ф = 0、 Я а) парабола при 4AC= B * t B) 4i4c> 5 *овал、 В) гипербола на 4 Это утверждение ничего не доказывает. в N°4.Образцы. Гипербола из-за асимптот. 1) рассмотрим уравнение 8x *-16 * + память+ 12y-4 =

0 Перепишите в форму 8С 1-2лг) + ЗСУ, — н > 0 = 4 Или дополните выражение в скобках до полного квадрата、 8 (f-2 * + 1)+ ЗСУ* + 4 >> + 4）= 24。 Отсюда (

!) ’. (y + 2) ’ 3 1 8 Перемещая начало координат в точку Oi (l, −2), мы делаем параллельный перенос системы. На новой оси уравнение линии имеет вид: 3 + 4- Он представляет собой эллипсоид с полу-оси Y3 и г-8.Этот трюк (новый! Обратите внимание,

что он находится на оси ординаты). 2) анализируйте более сложные примеры 4gv + 24hu + Tsu1-24kh-82u + 15 =0.(22） Начните с нахождения угла 0. Исчезновение произведения координат. Согласно (21) = Дж 482v = 4 ^ P = _T-123） Потому Что L = 4, B = 24, C = 11、 в pa 2tg6 О I A 2tg0 24 Итак, tgO — это 2-е уравнение^ _ q = — y или 12 tg90-7 tg 6-12 = 0. 4, 3.

Это уравнение удовлетворяет tg0 = -J и ТГ б= -. Неинтересно брать 0 из этих углов, потому что любой из этих углов удовлетворяет соотношению (23), но это все, что вам нужно. Возьмите по мере необходимости Угол 0 — это угол tg =0-.As [известно cos0 =± Так и в нашем случае cos0=:+=!(24)） И затем грех 0 = tg0cos0=± -^. (25） Выбор символов равенства (24) и, следовательно, (25) также свободен здесь. Конечно.、 Четыре если вы выберете tgO= -^, вы уже заявили,

что это гарантирует реализацию соотношения(23).Выберите Войти (24) cos 9 = 4. грех 0 = 4 ″» Формула преобразования координат при повороте системы на этот угол 0 принимает следующий вид: ДжейТи = а£л-4yLi у = у * У1. (26） Назначьте эти выражения выражению (22) в виде 4 >-y -1 bdg,-bu,+ 3 = 0.(27 )） Естественно, новое уравнение не включает в себя произведение. Выполните дальнейшие преобразования, как в предыдущем примере. То есть, напишите(27)

в виде: 4（>-4 * 1 + 4）-（y!+ 6y1 + 9)= 4 Или 1 4 Затем сделайте параллельный перенос системы и переместите начало координат в точку Oj (2, −3).Если вновь приобретенные оси обозначаются 0 \ X% и 0 ^ ur, то для xx = x2—2, yx = yb-3, а для оси 0 \ X^ уравнение прямой принимает вид: −1 т т т т Итак, эта линия является гиперболой

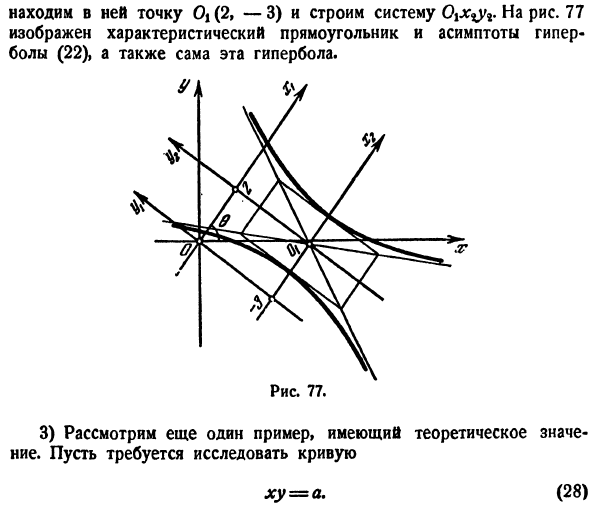
полуосей 1 и 2.Асимптотическая линия оси oijc| V имеет уравнение y1 =±2x%.Центром симметрии гиперболы является точка Oj. [В системе ohuh его координаты Xi = 2, yi =-3.So, согласно (26) системы Ohu, координаты точки 0\: = 3.6 и j»=-0.2. Чтобы нарисовать гиперболу на чертеже, сначала 3 4 поверните систему на угол cos0 = y, sin 6= -^ -. Этот угол находится в диапазоне от 0 до 90°и может быть легко настроен из тригонометрии известным способом. Если вы получаете

систему Ox / y / таким образом、 Найдите в нем точку Ot (2, −3) и постройте систему 77 Показаны характерные прямоугольники и асимптоты гиперболы(22), а также сама эта гипербола. 3) Рассмотрим другой пример, важный в теории. Нам нужно посмотреть на кривую. Ху = А. (28） Поскольку в этом уравнении A = C (=0), по замечаниям 1), система должна быть повернута на 45°.Для

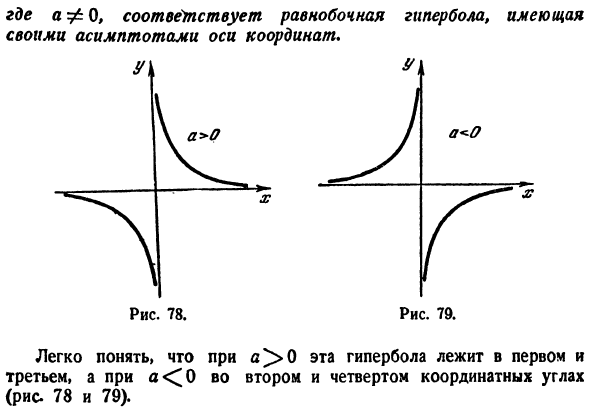
значения этого угла, равного 0, форма выражения преобразования координат имеет вид Если вы подставите эти выражения в (28)、 Си-ильный = 2а、 (29） (28） И это равносторонняя гипербола (в af 0).Его асимптоты делят пополам углы между осями симметрии. Но ось симметрии гиперболы (29) является новой! Это координатная ось, поэтому асимптота-это старая координатная ось. Таким образом,

теорема 4 доказана. Ху = А Здесь afO соответствует равносторонней гиперболе и имеет осевые асимптоты координатных осей. Это первая гипербола、 Если 3-й, 2-й и 4-й координатные углы равны 0(рис.78 и 79).

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Парабола

Элементы параболы
0F — фокальная ось
0 — вершина
— фокус
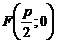
ε=1 — эксцентриситет
— фокальный радиус
— директриса
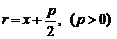
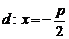
p — фокальный параметр

Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y 2 =2px
При p x 2 =2py
При p>0 ветви параболы направлены вверх, при p 2 /2+(y-1) 2 /2=1, необходимо набрать в поле x^2/2+(y-1)^2/2=1 и нажать кнопку График параболы .

Самостоятельно построить график можно, используя операцию выделения полного квадрата.

Каноническое уравнение параболы

Вы будете перенаправлены на Автор24

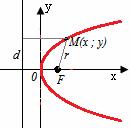
Парабола — это кривая, образованная геометрическим множеством точек, находящихся на одинаковом расстоянии от некой точки $F$, называемой фокусом и не лежащей ни на этой кривой, ни на прямой $d$.

То есть отношение расстояний от произвольной точки на параболе до фокуса и от этой же точки до директрисы всегда равно единице, это отношение называется эксцентриситетом.

Термин “эксцентриситет” также используется для гипербол и эллипсов.

Основные термины из канонического уравнения параболы

Точка $F$ называется фокусом параболы, а прямая $d$ — её директрисой.

Осью симметрии параболы называется прямая, проходящая через вершину параболы $O$ и её фокус $F$, так, что она образует прямой угол с директрисой $d$.

Вершиной параболы называется точка, расстояние от которой до директрисы минимальное. Эта точка делит расстояние от фокуса до директрисы пополам.

Что из себя представляет каноническое уравнение параболы

Каноническое уравнение параболы довольно простое, его несложно запомнить и оно имеет следующий вид:

$y^2 = 2px$, где число $p$ должно быть больше нуля.

Число $p$ из уравнения носит название «фокальный параметр».

Данное уравнение параболы, вернее именно эта наиболее часто применяемая в высшей математике формула, применимо в том случае, когда ось параболы совпадает с осью $OX$, то есть парабола располагается как будто на боку.

Парабола, описанная уравнением $x^2 = 2py$ — это парабола, ось которой совпадает с осью $OY$, к таким параболам мы привыкли в школе.

А парабола, которая имеет минус перед второй частью уравнения ($y^2 = — 2px$), развёрнута на 180° по отношению к каноничной параболе.

Готовые работы на аналогичную тему

Парабола является частным случаем кривой 2-ого порядка, соответственно, в общем виде уравнение для параболы выглядит точно также как для всех таких кривых и подходит для всех случаев, а не только когда парабола параллельна $OX$.

При этом дискриминант, вычисляющийся по формуле $B^2 – 4AC$ равен нулю, а само уравнение выглядит так: $Ax^2 + B \cdot x \cdot y + C\cdot y^2 + D\cdot x + E\cdot y + F = 0$

Вывод с помощью графика канонического уравнения для параболы

Рисунок 1. График и вывод канонического уравнения параболы

Из определения, приведённого выше в данной статье, составим уравнение для параболы с верхушкой, расположенной на пересечении координатных осей.

Используя имеющийся график, определим по нему $x$ и $y$ точки $F$ из определения параболической кривой, данного выше, $x = \frac

<2>$ и $y = 0$.

Для начала составим уравнение для прямой $d$ и запишем его: $x = — \frac

<2>$.

Для произвольной точки M, лежащей на нашей кривой, согласно определению, справедливо следующее соотношение:

$FM$ = $ММ_d$ (1), где $М_d$ — точка пересечения перпендикуляра, опущенного из точки $M$ c директрисой $d$.

Икс и игрек для этой точки равны $\frac

<2>$ $y$ соответственно.

Запишем уравнение (1) в координатной форме:

Теперь для того чтобы избавиться от корня необходимо возвести обе части уравнения в квадрат:

После упрощения получаем каноническое уравнение параболы: $y^2 = px$.

Парабола, описываемая с помощью квадратичной функции

Уравнение, описывающее параболу с верхушкой, расположенной где угодно на графике и необязательно совпадающей с пересечением осей координат, выглядит так:

Чтобы вычислить $x$ и $y$ для вершины такой параболы, необходимо воспользоваться следующими формулами:

$y_A = — \frac<4a>$, где $D = b^2 – 4ac$.

Пример составления классического уравнения параболы

Задача. Зная расположение фокусной точки, составить каноническое уравнение параболы. Координаты точки фокуса $F$ $(4; 0)$.

Так как мы рассматриваем параболу, график которой задан каноническим уравнением, то её вершина $O$ находится на пересечении осей икс и игрек, следовательно расстояние от фокуса до вершины равно $\frac<1><2>$ фокального параметра $\frac

<2>= 4$. Путём нехитрых вычислений получим, что сам фокальный параметр $p = 8$.

После подстановки значения $p$ в каноническую форму уравнения, наше уравнение примет вид $y^2 = 16x$.

Как составить уравнение параболы по имеющемуся графику

Рисунок 2. Каноническое уравнение для параболы график и пример для решения

Для начала необходимо выбрать точку $М$, принадлежащую графику нашей функции, и, опустив из неё перпендикуляры на оси $OX$ и $OY$, записать её икс и игрек, в нашем случае точка $M$ это $(2;2)$.

Теперь нужно подставить полученные для этой точки $x$ и $y$ в каноническое уравнение параболы $y^2 = px$, получаем:

Сократив, получаем следующее уравнение параболы $y^2 = 2 \cdot x$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021