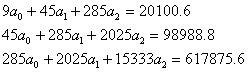Построение доверительных интервалов для коэффициентов регрессии
§ 8. Построение доверительных интервалов для коэффициентов регрессии
Найденные по МНК из нормальной системы значения коэффициентов регрессии, само уравнение регрессии – это не истинные значения, а приближенные, как и все, что мы находим по статистическим данным.
Те же самые формулы для другой серии наблюдений дадут и другие результаты, немного отличающиеся.
Для истинных значений мы можем построить доверительные интервалы:
Истинные значения коэффициентов с заданной вероятностью g будут лежать в построенных интервалах.
Размах доверительных интервалов определяется формулами:


Рекомендуемые файлы
Здесь коэффициент 


Чем меньше разброс статистических данных относительно построенной линии регрессии, тем меньше дисперсия и стандартное отклонение остатков, тем уже доверительные интервалы.
С другой стороны размах доверительных интервалов можно уменьшить, увеличивая объем выборки n, т.е. количество наблюдений.
Доверительная зона для линии регрессии
Уравнения регрессии – это тоже не истинные уравнения, это приблизительное знание о них. И подсчитанные по ним теоретические значения фактора Y, т.е. 

Размах доверительных интервалов определяется формулой:
Если подсчитать эти значения 
IV. Прогноз и его доверительный интервал
Прогноз — научное предвидение вероятностных путей развития экономических процессов в более-менее удаленном будущем.
Период упреждения — промежуток времени от момента, для которого есть последние статистические данные до момента, которому принадлежит прогноз.
Для прогнозируемого значения доверительный интервал определяется:
Коэффициент эластичности — в экономических задачах применяется для оценки влияния некоторого фактора (х) на соответствующий показатель (y).
В общем случае, статистический коэффициент эластичности, как правило, определяется на основе статистического ряда:
Точные значения коэффициента эластичности получают на основании операции предельного перехода, при 
kx будет определяться для парной регрессии:
для коэффициентов регрессии
Найденные значения коэффициентов ( a, b, c, d ) в уравнениях регрессии – это не истинные значения, это только оценка для них. (Как и любая другая информация, которую мы получаем по выборочным, статистическим данным
7. Построение доверительной зоны для линии регрессии
Уравнения регрессии – это тоже не истинные уравнения, это приблизительное знание о них. И подсчитанные по ним теоретические значения фактора Y, т.е. 

Размах доверительных интервалов определяется формулой:
Если подсчитать эти значения 
· В столбце BL ( ΔYi ) вычислить доверительные интервалы для 
Выделяя весь столбец, программируем формулу
Для чисел ( Sост , n ,


· В столбцах BM «нижн грань» и BN «верхн грань» вычислить границы
доверительной зоны.: 
Выделять весь столбец, программировать формулу с именами. Закончить ввод сочетанием Ctrl + Enter.
· Построить график доверительной зоны. Для этого выделить пять столб-
цов данных (вместе с заголовками):
¨ столбец N, в котором находятся статистические данные для фактора X.
¨ нажав клавишу Ctrl:
§ столбец O для фактора Y,
§ столбец AG для линии регрессии Y на X,
§ столбцы BM и BN для границ доверительной зоны.
Затем вызвать Мастер Диаграмм и построить Точечную Диаграмму. Отредактировать ее, так чтобы точки, указывающие линию регрессии и линии границы доверительной зоны на графике были линиями без маркеров ( желательно линию регрессии и границы – разным цветом). График должен выглядеть так же, как приведенный выше.
8. Определение прогноза и доверительного интервала для прогноза
Построенное уравнение регрессии можно теперь использовать для прогнозирования. Задавая любое значение фактора X можно подсчитать соответствующее среднее значение фактора Y.
Найденное таким образом значение, во–первых среднее, а во–вторых, опять таки, приблизительное. Истинное прогнозное значение с заданной вероятностью γ следует ожидать в доверительном интервале 
Размах доверительного интеграла для прогноза определяется формулой, почти такой же, как и при построении доверительной зоны:
· В ячейку BS29 скопировать из N23 заданное для прогноза значение Xp.
· В ячейке BV29 вычислить по найденной формуле регрессии прогнозное значение Yp :
· Размах доверительного интервала для прогноза найти в ячейке BS32 по приведенной формуле
· В ячейках BU32 и BW32 подсчитать границы доверительного интервала для прогноза:
§ 9. Прогноз и доверительные интервал для прогноза
Построенное уравнение регрессии можно теперь использовать для прогнозирования. Задавая любое значение фактора X можно подсчитать соответствующее среднее значение фактора Y.
Найденное таким образом значение, во–первых среднее, а во–вторых, опять таки, приблизительное. Истинное прогнозное значение с заданной вероятностью γ следует ожидать в доверительном интервале 
Размах доверительного интеграла для прогноза определяется формулой, почти такой же, как и при построении доверительной зоны:
Пример нахождения доверительных интервалов коэффициентов регрессии
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Постройте уравнение зависимости экспорта нефти от цены на нефть.
3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.
4. Оцените полученные результаты, выводы оформите в аналитической записке.
Таблица 5
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 119 | 298.12 | 14161 | 88875.53 | 35476.28 | 219.63 | 232120.8 | 6160.56 | 24362.01 |
| 203 | 481.03 | 41209 | 231389.86 | 97649.09 | 521.16 | 89328.76 | 1610.26 | 5196.01 |
| 281 | 539.12 | 78961 | 290650.37 | 151492.72 | 801.15 | 57979.42 | 68658.51 | 35.01 |
| 305 | 653.57 | 93025 | 427153.74 | 199338.85 | 887.3 | 15961.59 | 54628.94 | 895.01 |
| 381 | 987.66 | 145161 | 975472.28 | 376298.46 | 1160.11 | 43160.41 | 29738.57 | 11218.34 |
| 363 | 1252.85 | 131769 | 1569633.12 | 454784.55 | 1095.5 | 223673.03 | 24760.35 | 7729.34 |
| 389 | 1276.88 | 151321 | 1630422.53 | 496706.32 | 1188.83 | 246980.01 | 7753.57 | 12977.01 |
| 387 | 1396.70 | 149769 | 1950770.89 | 540522.9 | 1181.65 | 380430.93 | 46248.04 | 12525.34 |
| 315 | 952.03 | 99225 | 906361.12 | 299889.45 | 923.19 | 29625.58 | 831.49 | 1593.34 |
| 217 | 619.96 | 47089 | 384350.4 | 134531.32 | 571.41 | 25583.74 | 2356.85 | 3373.67 |
| 149 | 384.40 | 22201 | 147763.36 | 57275.6 | 327.32 | 156427.5 | 3258.23 | 15897.01 |
| 192 | 516.59 | 36864 | 266865.23 | 99185.28 | 481.67 | 69336.98 | 1219.24 | 6902.84 |
| 3301 | 9358.91 | 1010755 | 8869708.45 | 2943150.82 | 9358.91 | 1570608.75 | 247224.62 | 102704.92 |
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.4906
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)
Статистическая значимость коэффициента регрессии b не подтверждается (1.46 Fkp, то коэффициент детерминации статистически значим.
Доверительные интервалы для зависимой переменной
Уравнение тренда имеет вид y = at 2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
Для наших данных система уравнений имеет вид (см. таблицу).
Получаем a0 = -11.37, a1 = 88.47, a2 = 2151.09
Уравнение тренда: y = -11.37t 2 +88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая
| t | y | t 2 | y 2 | x ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y | t 3 | t 4 | t 2 y |
| 1 | 2225.3 | 1 | 4951960.09 | 2225.3 | 2228.19 | 65.6099 | 8.352 | 16 | 6431.117 | 1 | 1 | 2225.3 |
| 2 | 2254.9 | 4 | 5084574.01 | 4509.8 | 2282.55 | 462.25 | 764.5225 | 9 | 62347.985 | 8 | 16 | 9019.6 |
| 3 | 2332.3 | 9 | 5439623.29 | 6996.9 | 2314.17 | 9781.21 | 328.6969 | 4 | 42284.599 | 27 | 81 | 20990.7 |
| 4 | 2365.8 | 16 | 5597009.64 | 9463.2 | 2323.05 | 17529.76 | 1827.5625 | 1 | 101137.95 | 64 | 256 | 37852.8 |
| 5 | 2295.4 | 25 | 5268861.16 | 11477 | 2309.19 | 3844 | 190.1641 | 0 | 31653.566 | 125 | 625 | 57385 |
| 6 | 2303.9 | 36 | 5307955.21 | 13823.4 | 2272.59 | 4970.25 | 980.3161 | 1 | 72135.109 | 216 | 1296 | 82940.4 |
| 7 | 2166.7 | 49 | 4694588.89 | 15166.9 | 2213.25 | 4448.89 | 2166.9025 | 4 | 100859.885 | 343 | 2401 | 106168.3 |
| 8 | 2080.4 | 64 | 4328064.16 | 16643.2 | 2131.17 | 23409 | 2577.5929 | 9 | 105621.908 | 512 | 4096 | 133145.6 |
| 9 | 2075.9 | 81 | 4309360.81 | 18683.1 | 2026.35 | 24806.25 | 2455.2025 | 16 | 102860.845 | 729 | 6561 | 168147.9 |
| 45 | 20100.6 | 285 | 44981997.26 | 98988.8 | 20100.51 | 89317.2199 | 11299.312 | 60 | 625332.964 | 4050 | 30666 | 1235751.2 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 4.8518
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L — период упреждения; уn+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; Tтабл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79
K1 = 247.4924
1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49
K2 = 261.9213
1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45
K3 = 278.0099
1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67
K4 = 295.4871
1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15
K5 = 314.1213
1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается
Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.895):
(a — tтабл·Sa; a + tтабл·Sa)
(-20.5642;-2.1758)
(b — t табл·Sb; b + tтаблS·b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.
Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i — e i-1 ) 2 |
| 2225.3 | 2228.19 | -2.89 | 8.3521 | 0 |
| 2254.9 | 2282.55 | -27.65 | 764.5225 | 613.0576 |
| 2332.3 | 2314.17 | 18.13 | 328.6969 | 2095.8084 |
| 2365.8 | 2323.05 | 42.75 | 1827.5625 | 606.1444 |
| 2295.4 | 2309.19 | -13.79 | 190.1641 | 3196.7716 |
| 2303.9 | 2272.59 | 31.31 | 980.3161 | 2034.01 |
| 2166.7 | 2213.25 | -46.55 | 2166.9025 | 6062.1796 |
| 2080.4 | 2131.17 | -50.77 | 2577.5929 | 17.8084 |
| 2075.9 | 2026.35 | 49.55 | 2455.2025 | 10064.1024 |
| 11299.3121 | 24689.8824 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Между
и
существует линейное соотношение: для любых пар
данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.
- Остатки нормально распределены с нулевым средним значением;
- Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин
Если нанести остатки против предсказанных величин
от
мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением
то это допущение не выполняется;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
http://math.semestr.ru/corel/prim1.php
http://statistica.ru/theory/osnovy-lineynoy-regressii/