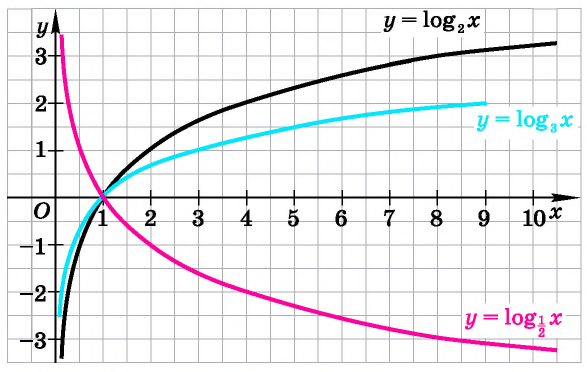
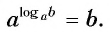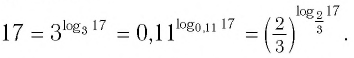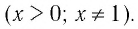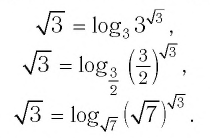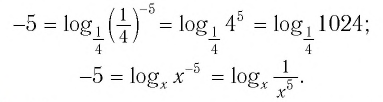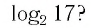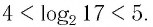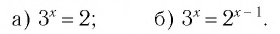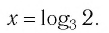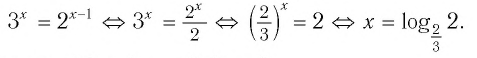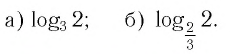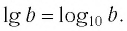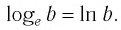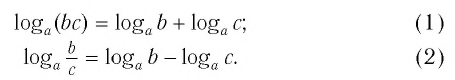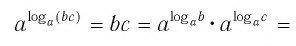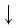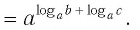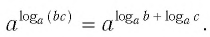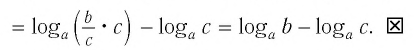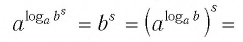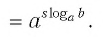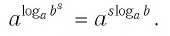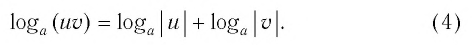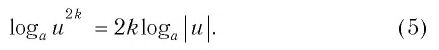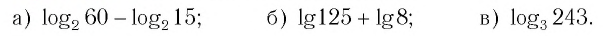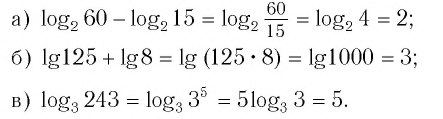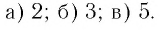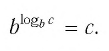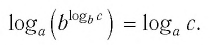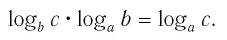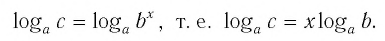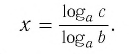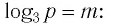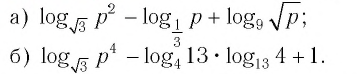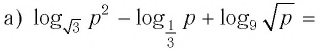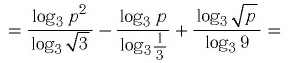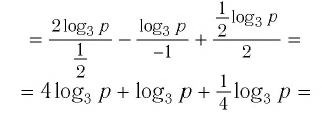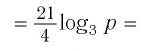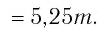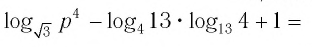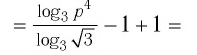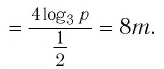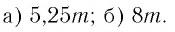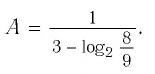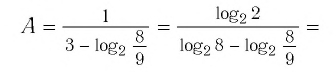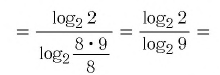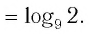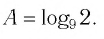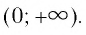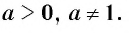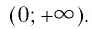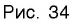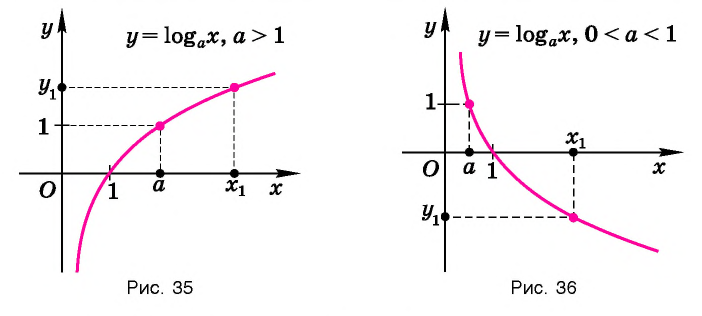Логарифм — формулы, свойства и примеры с решением
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 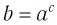
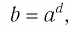
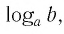
Таким образом, равенство 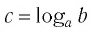
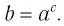
Определение:
Пусть 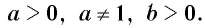
Приведем несколько примеров:
- а)
- б)
- в)
- г)
- д)
не имеет смысла, так как значение выражения
при любом значении х положительно и не может быть равно -9;
- е) по определению логарифма не имеют смысла и такие выражения, как
поскольку основанием логарифма должно быть положительное число, отличное от единицы.
Нахождение логарифма числа называется логарифмированием.
Обозначим 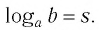
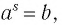
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 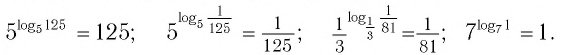
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 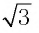
б) Записать число -5 в виде логарифмов по основанию 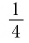
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 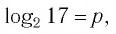
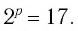
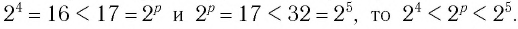
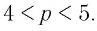
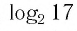
Ответ:
Пример:
Решение:
а) Поскольку 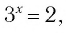
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 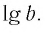
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Докажем утверждение (1).
По основному логарифмическому тождеству
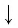
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 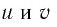
Следствие 2. При любом целом 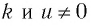
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 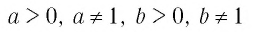
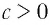
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 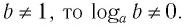
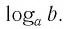
Способ 2. Пусть 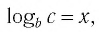
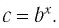
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




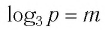
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
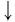
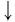
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 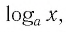
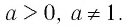
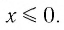
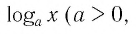
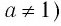
Определение:
Логарифмической функцией называется функция вида 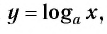
Область определения логарифмической функции — это естественная область определения выражения 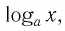
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 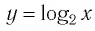
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 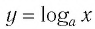
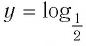
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 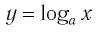
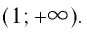
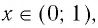
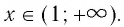
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Логарифм, история логарифмов и логарифмические уравнения
Логарифмические уравнения и решение логарифмических уравнений входят в обязательный комплекс знаний и умений школьника, если он стремится сдать ЕГЭ по математике на высокий балл и поступить в ВУЗ, стать студентом. Рассмотрим, что же это такое — логарифм, логарифмические уравнения и как их решать.
Логарифм — что это
Логарифмом числа по основанию
по основанию
(
=c)называется такой показатель степени
=c)называется такой показатель степени
, в которую нужно возвести
, чтобы получить
, чтобы получить
(то есть
). При этом задаются ограничения:
0, a\neq 1, b>0″ title=»Rendered by QuickLaTeX.com» height=»16″ width=»131″ style=»vertical-align: -4px;»/> ). При этом задаются ограничения:
0, a\neq 1, b>0″ title=»Rendered by QuickLaTeX.com»> . Значение
логарифма может быть любым.
,
,
.
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
.
2. При возведении , значит
, значит
.
Изобретенные в 17 веке для ускорения вычислений, логарифмы значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в числовой работе более 300 лет, пока совершенство механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделали их устаревшими для крупномасштабных вычислений. Однако натуральный логарифм (с основанием e ≅ 2.71828 и записываемый как ln n) продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.
Логарифмическая функция и ее график
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть . Подставим вместо
. Подставим вместо
разные числа и определим соответствующие значения переменной.
| 1 | 2 | 4 | ||
| -1 | 0 | 1 | 2 |
Отметим координаты точек на плоскости и соединим их плавной линией.
Логарифмическая функция все время возрастает.
Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь . Составим таблицу значений для этого случая.
| 1 | 2 | 4 | ||
| 1 | 0 | -1 | -2 |
Получим следующий график функции:
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять и логарифмы с натуральным основанием
и логарифмы с натуральным основанием
.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие, утомительные вычисления.
В частности, ученые могли найти произведение двух чисел m и n, посмотрев логарифм каждого числа в специальной таблице, сложив логарифмы, а затем снова сверившись с таблицей, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в терминах обычных логарифмов, эта связь определяется как log m n = log m + log n.
Например, 100 × 1000 можно рассчитать, просмотрев логарифмы 100 по основанию 10 и 1000
и 1000
. Сложив логарифмы
, а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.
Аналогично, задачи деления преобразуются в задачи вычитания с логарифмами: log m/n = log m — log n.
Это еще не все. Расчет степеней и корней может быть упрощен с использованием логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1).
В логарифмические таблицы обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа вне этого диапазона, число было сначала записано в удобном виде как произведение его значащих цифр и его степени по основанию 10 —
например, 358 будет записано как 3,58 × 10 2 ,
а 0,0046 будет записано как 4,6 × 10 -3 .
Тогда логарифм значащих цифр — десятичная дробь между 0 и 1, известная как мантисса — будет найдена в таблице. Например, чтобы найти логарифм 358, можно посмотреть таблицу значений логарифмов 3,58 ≅ 0,55388. Следовательно, lg 358 = lg 3,58 + lg 100 = 0,55388 + 2 = 2,55388.
В примере числа с отрицательным показателем степени, такого как 0,0046, можно посмотреть lg 4,6 ≅ 0,66276. Следовательно, lg 0,0046 = lg 4,6 + lg 0,001 = 0,66276 — 3 = -2,33724.
История логарифмов
Изобретению логарифмов предшествовало сравнение арифметических и геометрических последовательностей.
В геометрической последовательности каждый член образует постоянное соотношение (знаменатель прогрессии) с предыдущим и последующим членами прогрессии: например,… 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как разность прогрессии, например,… −3, −2, −1, 0, 1, 2, 3… имеет разность 1.
Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения, для приведенной выше примерной геометрической последовательности:… 10 −3 , 10 −2 , 10 −1 , 10 0, 10 1 , 10 2 , 10 3 ….
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равно суммированию соответствующих показателей степеней с основанием 10: -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение преобразуется в сложение.
Однако первоначальное сравнение между двумя возможностями вычислений произведения не было основано на каком-либо явном использовании экспоненциальной записи: это было последующее развитие.
В 1620 году в Праге швейцарским математиком Йостом Бурги была опубликована первая таблица, основанная на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Непер опубликовал свое открытие логарифмов в 1614 году. Его целью было помочь в умножении величин, которые были связаны с вычислением синуса в прямоугольном треугольнике.
Вычисления Непера и Бригса
В сотрудничестве с английским математиком Генри Бригсом Непер приспособил свой логарифм к его современной форме. Для неперова логарифма сравнение будет происходить между точками, движущимися по градуированной прямой линии, точка L (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, точка Х (для синуса) движется от нуля до бесконечности со скоростью пропорционально его расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорость в этой точке равна.
Суть открытия Непера состоит в том, что он связал между собой арифметические и геометрические прогрессии — то есть умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничивать движение L и X требованием, чтобы L = 1 при X = 10, в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бригиану, или общему логарифму.
Непер умер в 1617 году, а Бригс продолжил расчеты в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанную до 14 знаков после запятой для чисел от 1 до 20 000 и от 90 000 до 100 000. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги появилось только в 1857 году в Берлине.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — логарифмические линейки были незаменимы в инженерных расчетах.
Современное определение логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Где используются логарифмы
Некоторые области науки, где применяются логарифмы:
- Децибелы, используемые для измерения звукового давления, определяются с помощью логарифмов.
- Шкала Рихтера, которая используется для измерения интенсивности землетрясений, определяется с помощью логарифмов
- Значения pH в химии, которое используется для определения уровня кислотности вещества, также определяется с использованием понятия логарифма.
- Когда две измеренные величины оказываются связанными степенной функцией, параметры функции могут быть оценены с использованием логарифмов.
- Логарифмы могут быть использованы для решения уравнений, таких как 2 х = 3.
Решение логарифмических уравнений
Рассмотрим простейшие логарифмические уравнения и примеры их решения.
Задание 1
Решите уравнение log5(x 2 +x)=log5(x 2 +9)
Ответ:9
Решение: Так как основания логарифмов одинаковы, то числа, стоящие под знаком логарифмов — одинаковы:
,
Задание 2
Решите уравнение logx-5 49 = 2.
Если уравнение с логарифмами имеет более одного корня, в ответе укажите наибольший из них.
Ответ: 12
Решение:
x 2 – 10 x + 25 = 49;
x 2 – 10 x – 24 = 0;
a = 1 , b = -10, c = -24;
При х = –2 основание логарифма отрицательно (известно, что основание должно быть положительным). Решением является корень 12. Сделайте проверку.
Задание 3
Найдите корень уравнения log2(4 – x) = 7.
Ответ:-124
Решение:
Задание 4
Найдите корень уравнения .
Ответ: 115
Решение: 27=3 3 , тогда
или или
или
уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть:
. Тогда получим:
. Тогда получим:
.
Решая данное уравнение, получим: ,
.
Задание 5
Решите уравнение logx+725 = 2. Если уравнение имеет более одного корня, в ответе укажите наименьший из них.
Ответ: -2
Решение: .
0″ title=»Rendered by QuickLaTeX.com» height=»15″ width=»68″ style=»vertical-align: -2px;»/>,
-7″ title=»Rendered by QuickLaTeX.com» height=»13″ width=»54″ style=»vertical-align: 0px;»/> ,
-7″ title=»Rendered by QuickLaTeX.com»> .
и
и
и
и
Так как x должен быть больше -7, то корень не подходит. И остается один единственный корень:
не подходит. И остается один единственный корень:
.
Таким образом, уже не важно — наибольший это корень или наименьший, он один подходит. Поэтому в ответе указываем его.
Задание 6
Решите уравнение log2(2 – x) = log2(2 – 3x) + 1
Ответ: x=0,4.
Решение: мы знаем, что , тогда пусть в нашем случае
, тогда пусть в нашем случае
:
,
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
.
Задание 7
Решите уравнение log5(7 – x) = log5(3 – x) + 1
Ответ: 2
Решение: мы знаем, что , тогда пусть в нашем случае
, тогда пусть в нашем случае
:
.
применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:
.
Задание 8
Найдите корень уравнения
Ответ: x=-1
Решение:
.
так как у нас должно выполняться условие:
0\\ 4+x>0 \end
, откуда
, таким образом нам подходит только один корень
.
Итак, мы рассмотрели решение логарифмических уравнений с подробным решением каждого из них. Вы узнали, что такое логарифм, историю возникновения логарифма и имена ученых, которые схватили идею расчета произведения через сложение и изобрели логарифм, который на многие годы облегчил расчеты инженеров, строителей, ученых.
Формула корней квадратного уравнения
Таблица кубов натуральных чисел от 1 до 100
Как разложить на множители квадратный трехчлен
Сочинение на тему: Роман «История одного города» М.Е. Салтыкова-Щедрина — история России в зеркале сатиры
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,\;a> 0,\;a\neq 1′ alt=’b> 0,\;a> 0,\;a\neq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\\ x^<2>-4> 0\\ x^<2>+x=x^<2>-4 \end
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 \end
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\\ x> 0\\ x\neq 1 \end
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
http://novstudent.ru/logarifmicheskie-uravneniya/
http://ege-study.ru/logarifmicheskie-uravneniya/
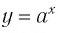
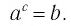
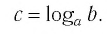
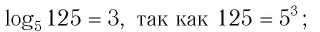
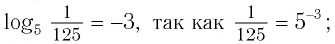
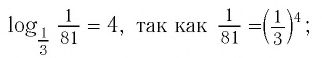
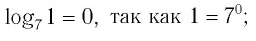
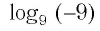 не имеет смысла, так как значение выражения
не имеет смысла, так как значение выражения 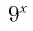 при любом значении х положительно и не может быть равно -9;
при любом значении х положительно и не может быть равно -9;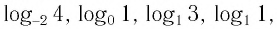 поскольку основанием логарифма должно быть положительное число, отличное от единицы.
поскольку основанием логарифма должно быть положительное число, отличное от единицы.