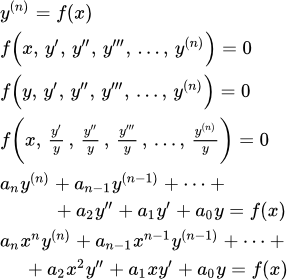Понятие об обыкновенных дифференциальных уравнениях высших порядков

Основные понятия и определения дифференциальных уравнений высших порядков

Дифференциальное уравнение n-го порядка имеет вид или, если оно разрешено относительно ,

Задача нахождения решения уравнения (I), удовлетворяющего начальным условиям

называется задачей Коши для уравнения (1).

Теорема существования и единственности решения задачи Коши . Если в уравнении (1) функция

а) непрерывна по всем своим аргументам в некоторой области их изменения,

б) имеет ограниченные в области частные производные по аргументам , то найдется интервал , на котором существует единственное решение уравнения (1), удовлетворяющее условиям

где значения содержатся в области .

Для уравнения второго порядка начальные условия имеют вид

где — данные числа. В этом случае теорема существования и единственности геометрически означает, что через данную точку плоскости с данным тангенсом угла наклона касательной проходит единственная кривая.

Рассмотрим, например, уравнение и начальные условия

В данном случае . Эта функция определена и непрерывна при всех значениях . Ее частные производные по и равны соответственно

и являются всюду непрерывными и ограниченными функциями своих аргументов. Следовательно, каковы бы ни были начальные условия

существует единственное решение данного уравнения, удовлетворяющее этим условиям.

Общим решением дифференциального уравнения n-го порядка (1) называется множество всех его решений, определяемое формулой , содержащей произвольных постоянных таких, что если заданы начальные условия (2), то найдутся такие значения , что будет являться решением уравнения (1), удовлетворяющим этим начальным условиям.

Любое решение, получаемое из общего решения при конкретных значениях произвольных постоянных называется частным решением дифференциального уравнения (1).

Уравнение вида , которое определяет неявно общее решение дифференциального уравнения, называется общим интегралом уравнения . Давая постоянным , конкретные допустимые числовые значения, получим частный интеграл дифференциального уравнения. График частного решения или частного интеграла называется интегральной кривой данного дифференциального уравнения.

Пример 1. Показать, что есть общее решение дифференциального уравнения .

Решение. Покажем, что удовлетворяет данному уравнению при любых значениях постоянных и . В самом деле, имеем .

Пусть теперь заданные произвольные начальные условия . Покажем, что постоянные и можно подобрать так, что будет удовлетворять этим условиям. Имеем . Полагая , получаем систему

из которой однозначно определяются и . Таким образом, решение удовлетворяет поставленным начальным условиям.

Геометрически это означает, что через каждую точку плоскости с заданным угловым коэффициентом проходит единственная прямая.

Задание одного начального условия, например , определяет пучок прямых с центром в точке , т.е. одного начального условия недостаточно для выделения единственного решения.

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 — ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 — это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n — 1 ) ( x 0 ) = f n — 1

где f 0 ; f 1 ; f 2 ; . . . ; f n — 1 — это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 — заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) — это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.