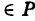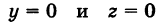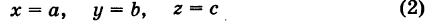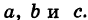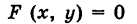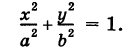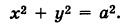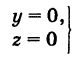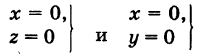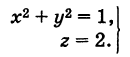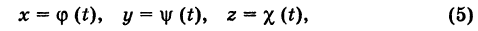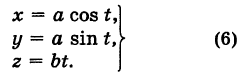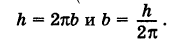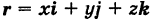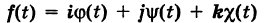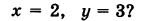Понятие об уравнении линии и поверхности. Полярная система координат.
Читайте также:
|
| sinφ = | | A · l + B · m + C · n | |
| √A 2 + B 2 + C 2 · √l 2 + m 2 + n 2 |
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
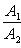

Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
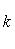

Это условие может быть записано также в виде
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
Уравнение прямой в пространстве: параметрические и канонические.
Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2, то уравнение прямой можно найти используя следующую формулу
| x — x1 | = | y — y1 | = | z — z1 |
| x2 — x1 | y2 — y1 | z2 — z1 |
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x0 |
| y = m t + y0 | |
| z = n t + z0 |
где (x0, y0, z0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n =
| x — x0 | = | y — y0 | = | z — z0 |
| l | m | n |
Уравнения плоскости.
Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x, y и z, которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.
Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.
Всякое уравнение вида 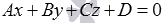
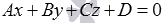
Уравнение 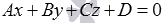
Уравнения поверхности и линии в пространстве с примерами решения
Содержание:
Уравнения поверхности и линии в пространстве
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если
— уравнение поверхности Р (рис. 189), то при М(х, у, z)
Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.
Пример (уравнения координатных плоскостей):
Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,
— уравнение координатной плоскости Oyz. Аналогично,
— соответственно уравнения координатных плоскостей Oxz и Оху.
Формула 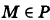
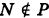
В более общем случае
— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные
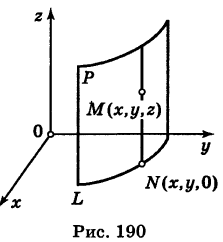
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.
Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 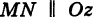
Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).
— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,
является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.
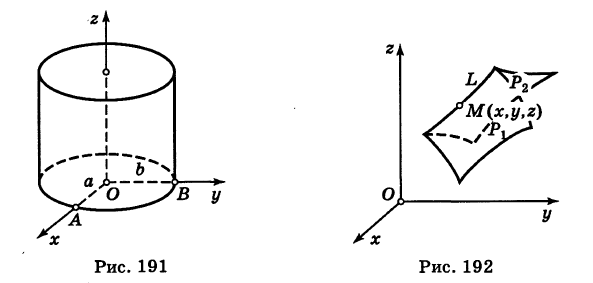
Пример (уравнение эллиптического цилиндра):
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение
В частности, при а = b получаем уравнение кругового цилиндра
Линию L в пространстве можно задать как пересечение двух данных поверхностей 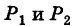

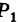
Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:
являющихся уравнениями поверхностей, определяющих данную линию.
Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки 
Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.
Определение: Уравнениями линии в пространстве 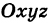
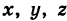
Пример (уравнения координатных осей):
Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому
— уравнения оси Ох. Аналогично,
— уравнения осей Оу и Oz соответственно.
Пример:
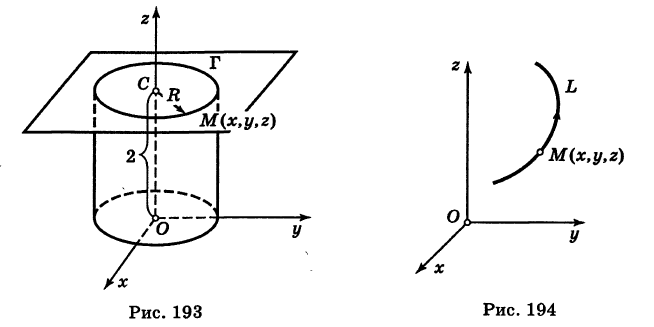
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).
Решение:
Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть
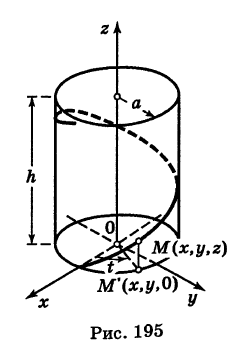
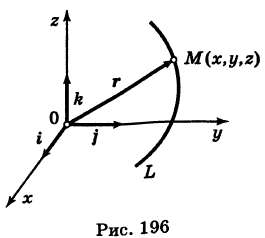
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем
где 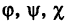
Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.
Пример:
Написать уравнения винтовой линии радиуса а и шага 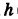
Решение:
Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.
Приняв за параметр 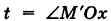
Для определения коэффициента пропорциональности b положим 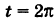
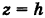
Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости 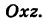
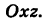
Текущую точку 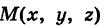
( 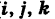
— так называемая вектор-функция скалярного аргумента t.
В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).
Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).
Пример:
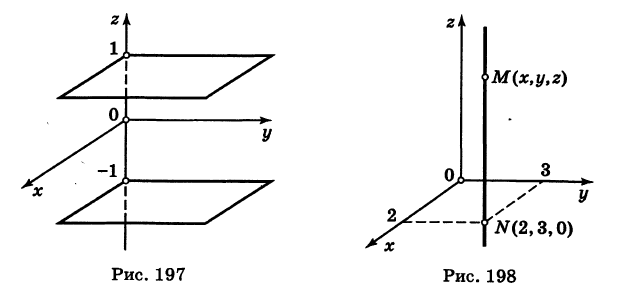
Какой геометрический образ соответствует уравнению
Решение:
Из уравнения (8) получаем 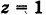
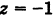
Пример:
Какой геометрический образ соответствует паре уравнений
Решение:
Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://megalektsii.ru/s41911t7.html
http://www.evkova.org/uravneniya-poverhnosti-i-linii-v-prostranstve




 должен быть одинаков со знаком y, а знак
должен быть одинаков со знаком y, а знак  — со знаком х.
— со знаком х.
 от заданной точки
от заданной точки  , называемойцентром окружности. Величина
, называемойцентром окружности. Величина 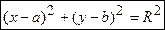 ,
, — радиус окружности.
— радиус окружности.

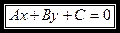 , (2)
, (2)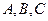 — постоянные коэффициенты, причём
— постоянные коэффициенты, причём  и
и  одновременно не обращаются в нуль
одновременно не обращаются в нуль  .
.
 — прямая проходит через начало координат;
— прямая проходит через начало координат;
 — прямая параллельна оси
— прямая параллельна оси  ;
;
 — прямая параллельна оси
— прямая параллельна оси  ;
;
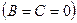 — прямая совпадает с осью
— прямая совпадает с осью 
 — прямая совпадает с осью
— прямая совпадает с осью