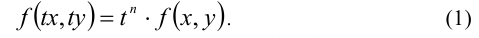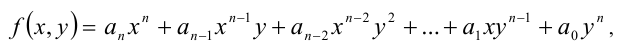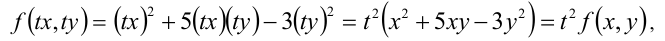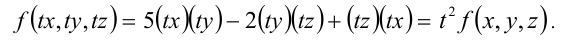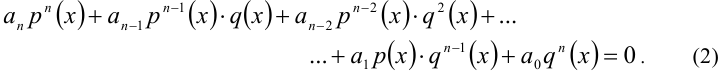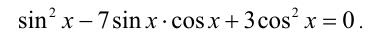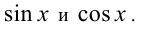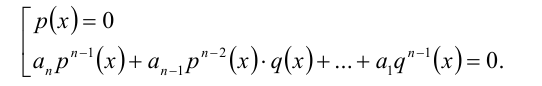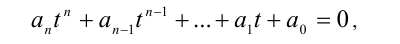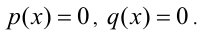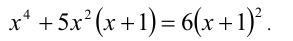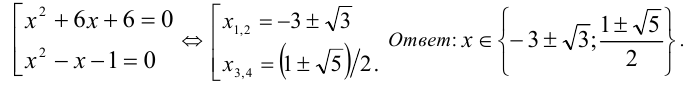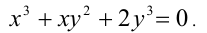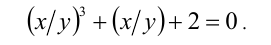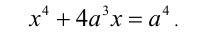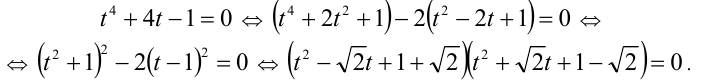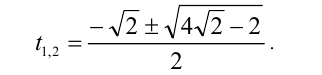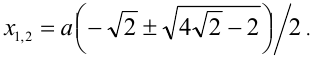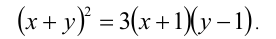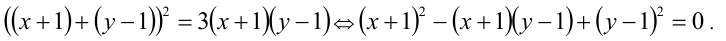Однородные уравнения
Разделы: Математика
Цели занятия:
- образовательные: – научиться распознавать однородные уравнения, отработать метод решения однородных уравнений.
- развивающие: – развивать логическое мышление, навыки самостоятельной работы и самоконтроля.
- воспитательные: – развивать познавательный интерес к предмету, творческие способности обучающихся.
Материал для лекции.
Определение: Многочлен 
Многочлен 
Например: 


Определение: Уравнение вида 


Понятие однородности распространяется и на уравнения с большим числом неизвестных.
Например: 
Однородное уравнение относительно 




Однородные уравнения
Однородные уравнения
Алгебраический многочлен f(x,y) с двумя переменными x и у называется однородным многочленом n -й степени относительно этих переменных 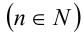
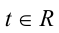
Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде
где 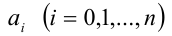
Уравнение f(x,y) = 0 называется однородным алгебраическим уравнением n -й степени с двумя неизвестными x,у, если f(x,y) — однородный многочлен n-й степени относительно этих переменных.
Например, уравнение вида 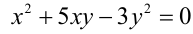
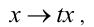
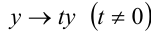
т.е. условие (1) из определения выполняется (n = 2).
Аналогично, уравнение 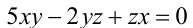
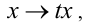
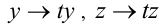
Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.
Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, 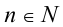
Однородным уравнением n -й степени относительно функций р(х), q(x) называется уравнение вида
В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида
Оно является однородным тригонометрическим уравнением 2-й степени относительно функций
Перейдём к процедуре решения уравнения (2).
Если хотя бы один из коэффициентов 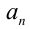
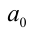
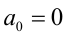
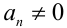
Если же 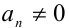
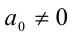
1) Если 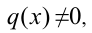
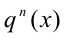
решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.
2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений
Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.
Пример №185.
Решить уравнение
Решение:
Перепишем уравнение: 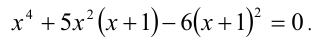
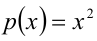
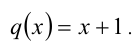
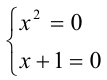
2) Пусть теперь 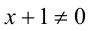
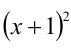
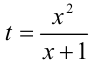
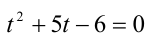
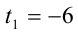
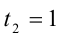
Пример №186.
Решить в целых числах уравнение
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть 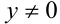
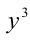
Обозначим t = x/у, тогда имеем кубическое уравнение 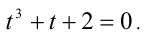
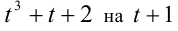
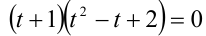
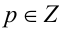
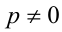
Ответ: 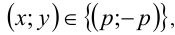
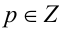
Пример №187.
Для каждого действительного значения параметра а решить уравнение
Решение:
Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.
1) Если а = 0 , то х = 0 .
2) Если 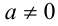
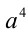
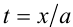
Первый сомножитель в нуль не обращается, а второй имеет два корня
Ответ: при а = 0 единственное решение x = 0 ;
при 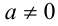
Пример №188.
Найти действительные корни уравнения
Решение:
Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду
Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.
1) Если 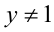
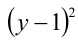
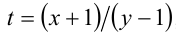
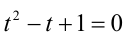
2) Если у = 1, то, подставляя в уравнение, находим x = — 1 .
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Однородные дифференциальные уравнения
и приводящиеся к ним
Однородные уравнения
Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .
Например, функция есть однородная функция второго измерения, так как
При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как
Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:
Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .
Пример 1. Решить однородное уравнение .
Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим
Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .
Отсюда общее решение: .
При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.
Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.
Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.
Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.
Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).
Уравнения, приводящиеся к однородным
А. Рассмотрим дифференциальное уравнение вида
где — постоянные, а — непрерывная функция своего аргумента .
Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.
Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.
1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду
Выбирая и как решение системы линейных уравнений
получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).
2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.
Пример 3. Решить уравнение .
Решение. Рассмотрим систему линейных алгебраических уравнений
Определитель этой системы .
Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид
Это уравнение является однородным уравнением. Полагая , получаем
Интегрируя, найдем или .
Возвращаемся к переменным :
Пример 4. Решить уравнение .
Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид
Разделяя переменные, получаем
Возвращаясь к переменным , получаем общий интеграл данного уравнения
Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .
Пример 5. Решить уравнение .
Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим
Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .
Положим ; исходное уравнение принимает вид
Положим теперь . Тогда это уравнение примет вид , откуда .
Разделяем переменные в этом уравнении . Интегрируя, найдем
Заменяя через , получаем общий интеграл данного уравнения
Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.
http://lfirmal.com/odnorodnyie-uravneniya-v-matematike/
http://mathhelpplanet.com/static.php?p=odnorodnye-differentsialnye-uravneniya