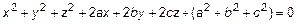Понятие поверхности вращения и вывод ее уравнения

Общее выражение поверхности вращения

Сфера

Метод сечений

Эллипсоиды

Цели занятия:изучить понятие поверхностей второго порядка; на основе полученных знаний по теме «Кривые второго порядка»; изучить метод сечений и научиться строить поверхности второго порядка.

Роль и место лекции

В предыдущих лекциях были даны такие понятия аналитической геометрии, как кривые второго порядка, плоскость и прямая в пространстве. Понимание этих тем особенно важно для восприятия данной лекции. Она позволит сформировать математическое пространственное мышление. Для лучшего усвоения материала необходимо рассматривать пространственные объекты в сечениях или в разрезе. Когда сформируется представление о геометрическом объекте, необходимо представить его в целом.

Предложенный материал особенно важен для тех специальностей, где необходимо строить геометрические модели объектов. Например, в географии при моделировании планетарных поверхностей и их участков, моделировании объемных тел залежей ископаемых; в программировании при компьютерной анимации (понятие «полигон» непосредственно связано с геометрическими фигурами в пространстве); в астрономии при построении траекторий движения космических тел; в биологии в вопросах, связанных с необходимостью исследования функций многих переменных, например зависимости популяции от среднегодовой температуры и широты местности, а так же при построении эквипотенциальных поверхностей и линий уровня.

Общее выражение поверхности вращения

Вывод уравнения поверхности

Определение 1

Поверхности второго порядка – это такие поверхности, которые описываются алгебраическими уравнениями второго порядка.

Поверхность вращения – поверхность, образованная вращением плоской кривой вокруг координатной оси.

Пусть дано уравнение кривой (рис. 1):

, (1)

где – текущие координаты кривой L. Т. е. Z=0 Образуем поверхность вращением L вокруг оси Oy. Возьмем некоторую точку на образованной поверхности . Проведем через эту точку плоскость . Обозначим – точка пересечения этой плоскости с осью Oy, а – точка пересечения этой плоскости с кривой L. Ординаты трех точек равны, поскольку лежат в одной плоскости , т. е. . Очевидно или ,

, или откуда . (2)

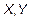
Подставим (2) в (1) получим уравнение

(3)

с тремя переменными , являющихся координатами точек поверхности, следовательно (3) есть уравнение поверхности вращения . Сравнивая (1) и (3) можно определить правило образования поверхности вращения.

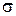
1.2. Правило образования поверхности вращения

Чтобы из уравнения кривой получить уравнение поверхности вращения надо в уравнении кривой оставить неизменной переменную, одноименную с осью вращения, а другую заменить корнем квадратным из суммы квадратов заменяемой переменной и недостающей в уравнении кривой.

Найти уравнение поверхности, образованной . Будем вращать кривую вокруг оси Ox. Согласно правилу образованная поверхность будет описываться уравнением или . Это уравнение сферы с центром в начале координат, R – радиус.

Сферой называется геометрическое место точек пространства, равноудаленных от одной точки – центра сферы.

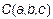
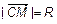
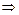
Зададим центр сферы , R – радиус. Тогда согласно определению определим выражение или

. (4)

Это уравнение сферы в каноническом виде. Раскроем скобки. Тогда уравнение (3) запишем в виде общего

алгебраического уравнения второго порядка. Т. е. сфера принадлежит к уравнениям второго порядка. Чтобы от общего уравнения перейти к каноническому надо выделить полные квадраты .

Признаки, характеризующие уравнение сферы:

— коэффициенты при квадратах текущих координат равны;

— отсутствуют члены, содержащие произведения текущих координат.

Изобразить тело, ограниченное поверхностями: , , .

Решение. В первом уравнении выделим полный квадрат или . Это сфера в центром . Уравнение – плоскость, проходящая через начала координат и ось . Тело отсекаемое этими поверхностями имеет вид (рис. 2).

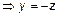
3. Метод сечений

Этот метод позволяет определить вид поверхности и изобразить ее. Метод сечений состоит в следующем.

1. Находят уравнения линий пересечения поверхности с координатными плоскостями или плоскостями параллельными им. При этом необходимо решать систему уравнений.

2. Изображая каждую линию сечения, получают изображение поверхности.

3. Два одинаковых типа сечений дают название поверхности, а третье сечение, отличное от двух одинаковых, дает определение к названию. Например, если в сечениях две параболы и один эллипс, следовательно, поверхность эллиптический параболоид.

Получим поверхность, вращая кривую – эллипс вокруг оси . Согласно правилу, уравнение поверхности будет иметь вид

. (5)

Для исследования этой поверхности применим метод сечений.

1. Сечение плоскостью , т. е. , тогда

или – эллипс.

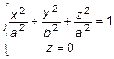
2. Сечение плоскостью , т. е. , тогда

или – окружность.

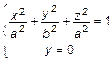
3. Сечение плоскостью , т. е. , тогда

или – эллипс.

Два эллипса, одна окружность, следовательно, это эллипсоид вращения рис. 3. Если эллипсоид вращения деформирован сжатием или растяжением в области кругового сечения, то получается трехосный эллипсоид или эллиптический эллипсоид

.

4.1. Однополостный гиперболоид

Получим поверхность, вращая кривую – гиперболу вокруг оси . Согласно правилу уравнение поверхности будет иметь вид

. (6)

Для исследования этой поверхности применим метод сечений.

1. Сечение плоскостью , т. е. , тогда

или

– окружность.

2. Сечение плоскостью , т. е. , тогда

или – гипербола.

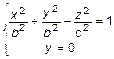
3. Сечение плоскостью , т. е. , тогда

или – гипербола.

То есть это гиперболоид вращения рис. 4.

4.2. Двуполостный гиперболоид

Получим поверхность, вращая кривую – гиперболу вокруг оси . Уравнение поверхности будет иметь вид

. (7)

Для исследования этой поверхности применим метод сечений.

1. Сечение плоскостью , т. е. , тогда

или – гипербола.

2. Сечение плоскостью , поскольку при решений нет (мнимая окружность), поэтому делаем сечение параллельной плоскостью, тогда

или – окружность. Отметим, что при

3. Сечение плоскостью , т. е. , тогда

или – гипербола.

Следовательно, это гиперболоид вращения рис. 5.

4.3. Эллиптический гиперболоид

Если гиперболоид вращения деформирован сжатием или растяжением в области кругового сечения, то получается эллиптический гиперболоид

;

.

В лекции дан метод сечений, используемый при построении поверхностей второго порядка. Понимание предложенного материала важно для изучения следующей лекции, посвященной параболоидам, цилиндрическим и коническим поверхностям. Важно понять, что аналитическая геометрия в пространстве отличается от аналитической геометрии на плоскости только лишней размерностью. Очевидно, что при необходимости можно рассматривать геометрические законы и в n-мерном пространстве. С точки зрения теории множеств поверхность – это отображение элементов множества декартовой плоскости (или упорядоченных пар) в элементы множества действительных чисел.

Отметим наиболее важное:

— поверхности второго порядка описываются уравнениями второго порядка;

— поверхности вращения образуются вращением плоской кривой второго порядка вокруг координатной оси;

— из уравнения кривой можно получить уравнение поверхности;

— если вращение осуществлять не по круговой, а по эллиптической траектории, то можно получить эллиптические поверхности;

— метод сечений заключается в рассмотрении кривых, образуемых при сечении поверхности некоторыми плоскостями

1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.

2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

Понятие поверхности вращения и вывод ее уравнения

Рассмотрим сечение плоскостью у = 0. Получается парабола = z, её ветви направлены вверх, вершина в точке (0, 0, 0).

Рассмотрим сечение плоскостью x = h. Это опять парабола:

Её ветви направлены вниз, вершина смещена по оси OZ на величину . то есть находится в точке . Заметим, что эта точка лежит на параболе

Теперь, изменяя h, видим, что поверхность гиперболического параболоида состоит из парабол, расположенных в плоскостях x = h, вершины которых находятся на параболе .

Поверхность вращения

§19. Поверхность вращения.

В этом параграфе будут рассмотрены поверхности, образованные вращением плоской кривой вокруг одной из координатных осей. Для определенности, возьмем кривую F(y, z) = 0 в плоскости YOZ и ось вращения ОZ . Зафиксируем произвольное значение z * и выразим из уравнения F(y, z * ) = 0 соответствующее значение у = f(z * ). При вращении, в плоскости z = z * получится окружность

x 2 + y 2 = f 2 (z * ). Уравнение самой поверхности вращения будет иметь вид x 2 + y 2 = f 2 (z) (рис.10).

Необходимо отметить, что аналитическое решение уравнения

z F(y, z * ) = 0 относительно у совсем не обязательно, тем более,

F(y, z) = 0 что оно может быть достаточно трудоемким, либо невозможным.

Поэтому, уравнение поверхности вращения в данном случае

записывается следующим образом: