Понятие рационального уравнения 8 класс

Конспект урока на тему: «Понятие рационального уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

8 класс алгебра

Дата проведения: 19.01.22г.

тема урока. Понятие рационального уравнения

Цели: ввести понятие рационального уравнения, формировать умение применять алгоритм решения рационального уравнения. Развивать математическую речь, логическое мышление, интерес к предмету. Воспитывать прилежание, трудолюбие, аккуратность, точность.

Личностные: умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности; критичность мышления, инициатива, находчивость, активность при решении математических задач.

Предметные : знать: формулу нахождения корней квадратного уравнения; уметь вычислять квадратные корни, применять понятие и свойства квадратного корня при решении различных задач, решать квадратные уравнения с помощью формулы нахождения корней квадратного уравнения

Тип урока: формирование умений и навыков

Формы работы: фронтальная, индивидуальная

Методы и приёмы: самостоятельная, устный счёт, сравнение

Оборудование: учебник, таблица

I. Организационный момент.

II. Проверка домашнего задания.

III. Устная работа.

1. Какие из выражений являются целыми, какие – дробными?

а) ; б) (а – b) 2 – 3ab; в) ;

г) ; д) ; е) .

2. Решить уравнение: 3х 2 -4х-4=0

IV. Объяснение нового материала.

Объяснение следует проводить в н е с к о л ь к о э т а п о в.

1. В в е д е н и е п о н я т и я рационального уравнения.

Во время проведения устной работы были актуализированы следующие знания учащихся: целые выражения, дробные выражения, рациональные выражения, допустимые значения переменных. Предлагаем учащимся самим сформулировать понятие дробного рационального уравнения. Следует акцентировать их внимание на то, что наличие дроби в выражении не свидетельствует о том, что это дробное выражение (уравнение), необходимо присутствие переменной в знаменателе дроби.

2. Р а с с м о т р е н и е а л г о р и т м а решения рационального уравнения.

Рассматривая способ решения дробного рационального уравнения, учащиеся используют приём аналогии: решая целое уравнение с числом в знаменателе, они умножают обе части уравнения на общий знаменатель, что позволяет избавиться от дробей. Возникает идея применить этот приём для нового вида уравнений. После домножения обеих частей уравнения на общий знаменатель, обращаем внимание учащихся, что произошло с областью допустимых значений уравнения. Она «расширилась» и теперь допустимыми стали любые значения переменных, то есть полученное уравнение не равносильно исходному.

Вопрос: как же следует поступить в этом случае? Затем формулируется алгоритм решения дробного рационального уравнения:

1) Найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить полученное целое уравнение;

4) исключить из его корней те, которые обращают в нуль

V. Формирование умений и навыков.

№291 а)да; б) да; в) да; г) да; д) да; е) да; ж) нет; з) нет; и)нет; к)нет.

а)если х=2, то 3*2 — = 2+5, 6 + = 7, 6+1=7, 7=7. Ответ: является.

б) если х = -0,1, то 3*(-0,1-8)=4-2*(-0,1-1), 3*(-8,1)=4-2*(-1,1), -24,3=4+2,2, -24,3=6,2. Ответ: не является.

в)если х = 3, то 3 2 +4*3-28=0, 9+12-28=0, -7=0. Ответ: не является.

г) если х = , то – 1 = , — : ( ) -1= , * -1= , — = , — = 1,35. Ответ: не является.

В о п р о с ы у ч а щ и м с я:

– Какое уравнение называется рациональным?

– Приведите примеры целого и рационального уравнения.

– Сформулируйте алгоритм решения рационального уравнения.

– Какими способами можно исключить «посторонние» корни рационального уравнения?

Домашнее задание: №292(д,е,ж,з), № 293(б,в,г,ж)

Рациональные уравнения с примерами решения

Содержание:

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.

Урок по теме арциональные уравнения.

Просмотр содержимого документа
«Понятие рационального уравнения. Решение простейших дробно-линейных уравнений.»

Конспект урока по теме «Рациональные уравнения»

знать, какое уравнение называется рациональным научиться решать рациональные уравнения;

Развивающие:
создать условия для развития мыслительных операций: наблюдения, сравнения, обобщения, конкретизации;
способствовать развитию математической речи; создать условия для развития познавательного интереса.

Воспитательные:
воспитывать навыки коммуникативности в работе, умение слушать другого, уважение к мнению товарища;
воспитывать у обучающихся такие нравственные качества, как настойчивость, аккуратность, инициативность, точность, самостоятельность, активность.

Тип урока: изучение нового материала.

Цели: создать деловой настрой для занятия; информировать о подготовке к уроку

Приветствует учащихся, отмечает их готовность к проведению урока.

2.Актуализация опорных знаний.

Цели: повторить основные понятия, необходимые на уроке, наметить шаги учебной деятельности

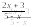
Закончите предложение:
«Дробь равна нулю тогда и только тогда, когда её числитель …
равен нулю, а знаменатель отличен от нуля.

При каких значения х данная дробь равна нулю?

Выберите правильный ответ слайд № 4

Как называются уравнения? Откуда вы их знаете? А как вы думаете, зачем ещё раз к ним вернулись? Слайд № 5

Работа с учебником: с. 94 – 95.
1) Рассмотреть пример 1.
2) Пробовать составить словесный алгоритм решения рационального уравнения. Каждому раздать.

Выполняем упражнения: 292(1 ст.), 293(1ст.)

— Какие уравнения решали?

— При решении рациональных уравнений в конце всегда надо сделать …

— Какой корень называют посторонним?

7.Подведение итогов учебной деятельности, домашнее задание.

Памятка «Правила работы в группе»

Слушай, что говорят другие

Делай выводы об услышанном, задавай вопросы

Говори спокойно, ясно, только по делу

Анализируй свою деятельность, вовремя корректируй недостатки