Порядок дифференциального уравнения цепи определяется
3.2 Электрические цепи первого порядка
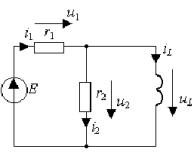
Порядок электрической цепи определяется числом реактивных элементов. Цепь первого порядка ( n = 1) включает один реактивный элемент — индуктивность или емкость и любое число резистивных элементов и независимых источников питания. По отношению к реактивному элементу всю остальную цепь можно считать резистивным активным двухполюсником (рис. 3.1а,б).
Рис. 3.1. Схематичное изображение цепи первого порядка:
а) RC -цепь; б) RL -цепь
Переходный процесс в такой цепи описывается дифференциальным уравнением первого порядка, решение которого для переменных состояния 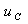
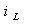
где p — корень характеристического уравнения. Эта величина вещественна и отрицательна, она выполняет роль коэффициента затухания. Обратное отношение 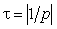
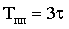
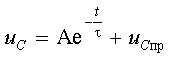
Итак, для того чтобы получить решение для переменных состояния 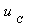
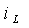
1. Постоянную времени τ 
2. Принужденную составляющую — 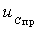
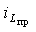
3. Постоянную интегрирования A.
Рассмотрим эту триединую задачу на примерах.
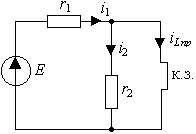
Пример 3.1. В цепи рис. 3.2а, которая питается от источника постоянного напряжения E , происходит замыкание ключа S. Найти закон изменения тока в индуктивности.
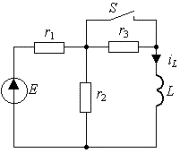
Рис. 3.2. Схема RL -цепи первого порядка:
а) исходная цепь( t б) схема после коммутации( t >0)
Предварительный анализ цепи показывает, что в процессе коммутации сопротивление 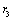
В соответствии с требованием классического метода для времени t>0 составим систему уравнений по законам Кирхгофа [1]
После подстановки компонентных соотношений, связывающих токи и напряжения в отдельных элементах цепи, получим
Подставим первое и третье уравнение во второе, чем сведем систему
к одному уравнению относительно переменной состояния 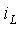
Уравнение для свободной составляющей режима получим, приравняв правую часть к нулю
Переход к характеристическому уравнению произведем заменой d/dt на p, а 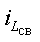
Найдем корень характеристического уравнения, модуль которого совпадает с коэффициентом затухания
Постоянную времени получим как величину обратную коэффициенту затухания
Анализ выражений (3.11) и (3.12) показывает, что постоянная времени, пропорциональна величине индуктивности L и обратно пропорциональна некоторому эквивалентному резистивному сопротивлению 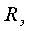
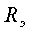
Входное сопротивление цепи определяется в три этапа:
а. Изображается схема цепи после коммутации ( t>0);
б. В этой цепи вместо реактивного элемента рисуют разомкнутые зажимы, по отношению к которым в дальнейшем определяют входное сопротивление. Далее исключают все источники энергии: источники напряжения замыкают накоротко, а источники тока разрывают;
в. Последовательно упрощают цепь, объединяя последовательно и параллельно соединенные резистивные элементы, чем сводят цепь к эквивалентному сопротивлению, которое и будет искомым входным 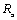
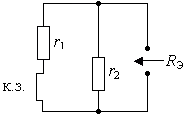
Рис. 3.3. Схема для определения Рис. 3.4. Схема для определения
входного сопротивления активного принужденной составляющей
Для рассматриваемой цепи такая преобразованная схема показана на рис.3.3. Здесь вместо индуктивности изображены разомкнутые зажимы, со стороны которых требуется определить входное сопротивление, а вместо источника напряжения E показана короткозамкнутая перемычка. Сопротивления 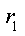
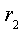
2. Принужденную составляющую решения определим для бесконечно большого момента времени ( t = 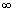
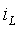
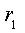
Используя выражение (3.7), сформируем решение в виде суммы свободной и принужденной составляющей:
3. Постоянную интегрирования A определим на основании первого за-
кона коммутации (3.1).Для момента времени t = 0 имеем 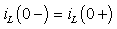
или 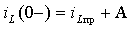
Отсюда следует общая формула определения постоянной интегрирования для цепей первого порядка, включающих одну индуктивность:
Для определения 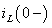
Рис. 3.5. Схема для анализа докоммутационного состояния цепи
Так как исследуемая цепь включает один источник энергии, то наиболее просто получить результат можно путем использования метода эквивалентных преобразований, вычисляя входное сопротивление цепи со стороны источника напряжения
Искомый ток 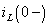
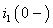
По формуле (3.13) окончательно определим постоянную интегрирования
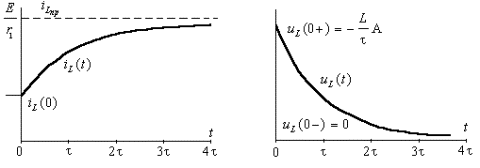
График функции тока 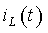
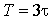
Найденное выражение для переменной состояния 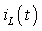
а. Напряжение на индуктивности:
Все найденные как следствие функции имеют разрыв в точке t = 0.
Рис. 3.6. Графики переходного процесса: а)ток в индуктивности; б)напряжение на индуктивности
Например, график функции 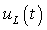
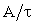
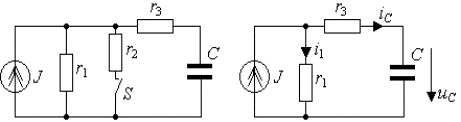
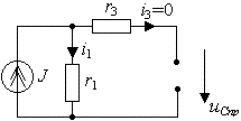
Пример 3.2. В цепи рис.3.7а найти закон изменения напряжения на емкости после размыкания ключа S, если цепь питается от источника постоянного тока J = const.
Предварительный анализ цепи показывает, что до размыкания ключа S ток источника протекал по параллельно соединенным сопротивлениям 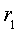
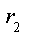
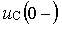
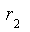
Рис. 3.7. Схема RC -цепи первого порядка:
а) исходная цепь ( t б) схема после коммутации ( t >0)
1. Составим систему уравнений цепи по законам Кирхгофа:
где переменной состояния для этой цепи будет напряжение 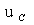
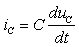
Как и следовало ожидать, переходный процесс описывается неоднородным дифференциальным уравнением первого порядка. Решение его имеет вид
Приравнивая нулю правую часть уравнения и делая замену 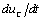
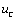
откуда определяется единственный корень 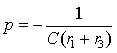
Постоянную времени цепи определим как модуль обратной величины от коэффициента затухания
Полученный результат, запишем в более общей форме
где 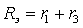
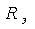
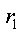
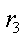
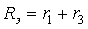
Второй способ определения быстрее приводит к поиску свободной составляющей режима, чем составление и решение системы уравнений.
2. Принужденную составляющую режима определим для бесконечно большого момента времени 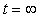
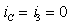
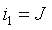
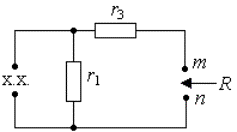
Рис. 3.8. Схема для определения Рис. 3.9. Схема для анализа
входного сопротивления принужденных составляющих
активного двухполюсника режима
Объединяя свободную и принужденную составляющую режима, получим:
3. Постоянную интегрирования A для выражения (3.15) найдем на основе второго закона коммутации (3.4):
Формула (3.16) имеет общий характер и ей можно пользоваться для цепей первого порядка при наличии емкостного элемента. Для определения 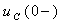
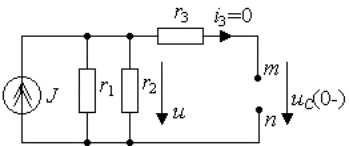
Рис. 3.10. Схема для анализа докоммутационного состояния цепи
Аналогично пункту 2 ток источника тока J создает падение напряжения на параллельно соединенных сопротивлениях 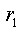
Это же напряжение приложено к разомкнутым зажимам m, n. Используя формулу (3.16), окончательно получим
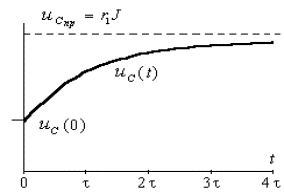
График переходного процесса для переменной 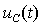
Рис.3.11. График переходного процесса напряжения на емкости
Как следствие решенной задачи можно найти токи и напряжения в других элементах цепи:
а. Ток в емкости и в резистивном сопротивлении r3
б. Напряжение на сопротивлении 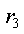
в. Напряжение на сопротивлениях 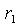
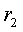
г. Токи в сопротивлениях 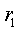
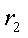
Все эти алгебраические преобразования достаточно очевидны. Полученные здесь как следствие функциональные выражения носят разрывный характер в точке t = 0 . Каждое из них можно определить непосредственно только после исследования цепи для момента времени t=0+,т.е. в первый момент после коммутации.
Рассмотренные здесь примеры показывают, что для цепей первого порядка нет необходимости составлять уравнения равновесия цепи, сводить эту систему к одному дифференциальному уравнению и решать соответствующее ему характеристическое уравнение. Достаточно найти входное резистивное сопротивление 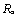
Общий вид решения для переменных состояния также известен:
Определение 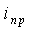
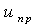
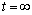
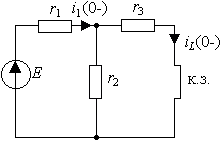
Численные значения iL (0-) и uC (0-) находятся для момента времени t=0-, который предшествует коммутации. Для каждого временного состояния цепи целесообразно составить расчетную схему замещения и, пользуясь любыми методами анализа цепи, определить требуемую переменную.
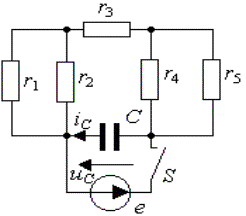
Пример 3.3. Для цепи, представленной на рис.3.12, найти закон изменения напряжения на емкости С после отключения от цепи идеального источника синусоидального напряжения
До размыкания ключа S в каждом элементе цепи протекал синусоидальный ток, обусловленный источником питающего напряжения. Емкость присоединена непосредственно к источнику напряжения, и напряжение на ней в каждый момент времени такое же, как и в источнике. К моменту коммутации это напряжение будет равно
и останется на емкости в первый момент после коммутации.
Рис. 3.12. Схема RC –цепи при питании от источника синусоидального напряжения
Переходный процесс в цепи будет развиваться за счет энергии, накопленной емкостью. В течение переходного процесса энергия электрического поля перейдет в тепловую энергию в резистивных элементах цепи. Следовательно, к концу переходного процесса напряжение на емкости станет равным нулю, что и определяет нулевое значение принужденной составляющей режима.
Проведенный предварительный анализ показывает, что переходный процесс в цепи будет определяться только свободной составляющей режима:
Постоянную времени определим по формуле (3.14), где 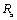
входное сопротивление цепи со стороны емкости:
Порядок дифференциального уравнения цепи определяется
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи
| Резистор (идеальное активное сопротивление) | |||||||
| Катушка индуктивности (идеальная индуктивность) | |||||||
| Конденсатор (идеальная емкость) | |||||||
 . . | (1) |
Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
 , , | (2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
 , , | (3) |
где 



Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение 

Частное решение 

Вторая составляющая 

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид
 | (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей 


Таблица 2. Законы коммутации
Первый закон коммутации (закон сохранения потокосцепления)
Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Второй закон коммутации (закон сохранения заряда)
Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения 

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
второй закон коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа 

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для 

Пример. Определить токи и производные 

В соответствии с законами коммутации


На основании второго закона Кирхгофа для момента коммутации имеет место

и 
Для известных значений 

определяется 
Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 
Таблица 3. Выражения свободных составляющих общего решения
Вид корней характеристического уравнения
Выражение свободной составляющей
Корни 
Корни 
Пары комплексно-сопряженных корней
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где 
Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Портал ТОЭ
6.2 Классический метод расчёта переходных процессов
Анализ переходного процесса в линейной цепи с сосредоточенными параметрами R , L , C (рис. 6.2 ) сводится к решению линейных неоднородных уравнений, выражающих законы Кирхгофа.
где i ( t ) – переходный ток.
Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:
Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.
Решение дифференциального уравнения:
где i пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.
Таким образом здесь используется метод наложения. Физически существует только i ( t ) , а разложение его на i пр и i св является математическим приёмом, облегчающим расчёт переходного процесса.
Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.
Для расчёта свободной составляющей следует найти корни характеристического уравнения p k и n постоянных интегрирования A k .
Если характеристическое уравнение
имеет n различных корней p k ( k = 1 , 2 , … ,n ) , то
Корню p k кратности m k ≥ 1 соответствует слагаемое свободной составляющей вида
Чтобы определить постоянные интегрирования A k , необходимо знать значения искомой величины и всех её производных до ( n − 1) порядка включительно в момент времени t = 0+ . Для их определения используются законы коммутации.
Составление характеристического уравнения
- Составляем уравнение электрического состояния цепи для свободного режима (т.е. при устранении вынужденной (принуждающей) силы). Это соответствует схеме с исключёнными источниками – источники ЭДС закорачиваются, ветви с источниками тока размыкаются.
Например для рис. 6.3 :
где Z вх ( p ) – входное сопротивление схемы относительно двух зажимов, получающихся в результате размыкания любой ветви схемы;
Y вх ( p ) – входная проводимость схемы относительно произвольной пары узлов схемы.
Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.
Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.
Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.
Рассмотрим схему на рис. 6.4 . Три реактивных элемента в упрощённой схеме определяют три независимых начальных условия, т.е. порядок характеристического уравнения равен трём.
Свободный процесс происходит в цепи, освобождённой от источников энергии, поэтому свободные токи не могут протекать сколь угодно долго в цепи, где есть активные элементы. Свободные токи должны затухать, в связи с этим действительные части корней p k характеристического уравнения должны быть отрицательными.
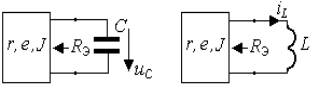
- Так, при наличии одного корня p = − a
http://toehelp.ru/theory/toe/lecture24/lecture24.html
http://toeportal.ru/lections/toe/6.2
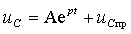
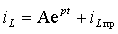
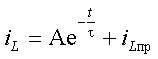
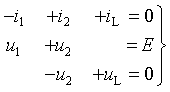
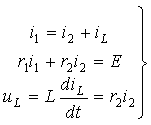
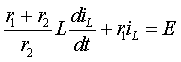
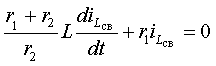
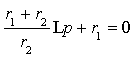
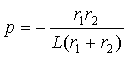
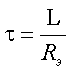
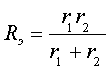
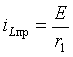
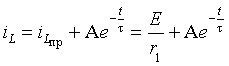
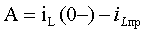
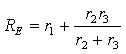
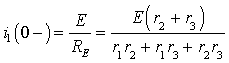
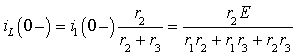
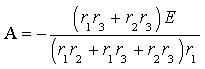
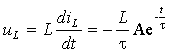
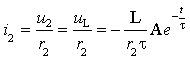
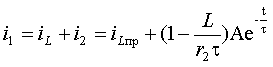
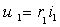
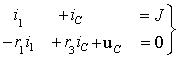
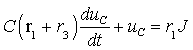
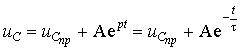
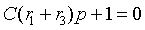
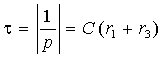
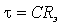
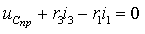
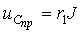
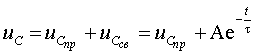
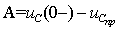
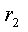
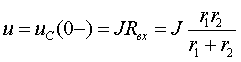
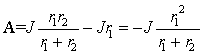
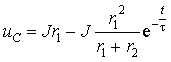
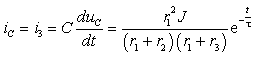
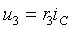
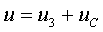
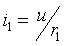
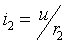
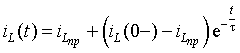
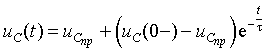
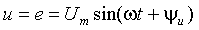
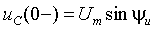
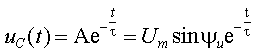

 ;
; ,
,
 ;
;












