Порядок лдс по разностному уравнению

B. Рекурсивные и нерекурсивные ЛДС

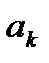
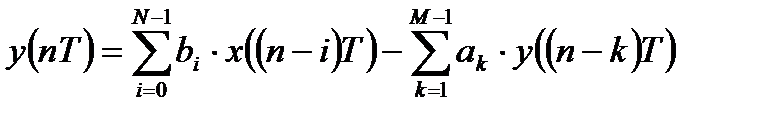
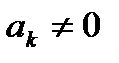
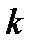
ЛДС называется рекурсивной, если хотя бы один из коэффициентов разностного уравнения не равен нулю:

, хотя бы для одного из значений . (1.1)

Порядком рекурсивной ЛДС называют наибольшую из величин ( , ).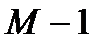

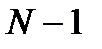
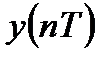
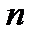
Согласно разностному уравнению, реакция рекурсивной ЛДС в каждый момент времени определяется:

— текущим отсчетом воздействия;

— предисторией реакции.

Так как при вычислении выходного сигнала используются предыдущие отсчеты выходного сигнала, то в схеме вычислений присутствуют обратные связи. Именно поэтому такие фильтры называются рекурсивными (recursive).

Разностное уравнение рекурсивной ЛДС первого порядка имеет вид:

. (1.2)

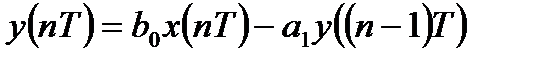
Разностное уравнение рекурсивной ЛДС второго порядка имеет вид:

. (1.3)

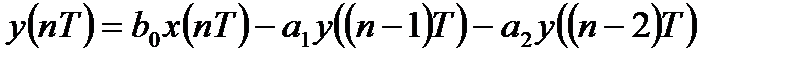
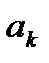
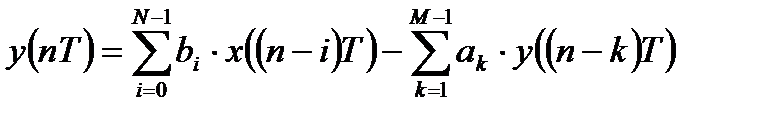
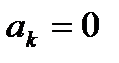
ЛДС называется нерекурсивной, если все коэффициенты разностного уравнения равны нулю:

. (1.4)

Для нерекурсивной ЛДС разностное уравнение принимает вид:

. (1.5)

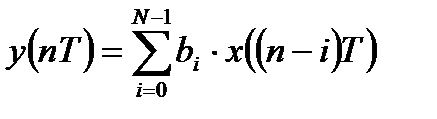
Порядком нерекурсивной ЛДС называют величину .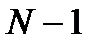

Реакция 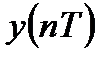нерекурсивной ЛДС определяется:

— текущим отсчетом воздействия;

Так как при вычислении выходного сигнала не используются предыдущие отсчеты выходного сигнала, то в схеме вычислений отсутствуют обратные связи. Поэтому такие фильтры называются нерекурсивными (nonrecursive). Применяется также термин «трансверсальный фильтр» от английского слова поперечный – transversal.

Разностное уравнение нерекурсивной ЛДС второго порядка имеет вид:

. (1.6)

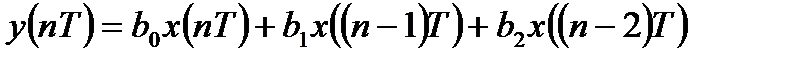
ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ

Лариса Антипина 5 лет назад Просмотров:

1 ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. БОНЧ-БРУЕВИЧА ФАКУЛЬТЕТ ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ А.И. Солонина, Д.А. Улахович ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ УЧЕБНОЕ ПОСОБИЕ, САНКТ-ПЕТЕРБУРГ 5

2 УДК Солонина А.И., Улахович Д.А. Линейные дискретные системы: учеб. пособие спец., / СПбГУТ. СПб, 5. Утверждено редакционно-издательским советом университета в качестве учебного пособия. Содержит основы теории линейных дискретных систем, типовые примеры выполнения контрольной работы, варианты заданий и рекомендуемую литературу. Рецензенты: проф. А.Е. Рыжков СПбГУТ проф. В.И. Воробьев ВАС А.И. Солонина, Д.А. Улахович, 5 Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича, 5

3 СОДЕРЖАНИЕ Введение. 4. Линейные дискретные системы: основы теории Аналоговые и дискретные сигналы. Нормирование времени Типовые дискретные сигналы Основная полоса частот. Нормирование частоты. Линейные дискретные системы Описание линейных дискретных систем во временной области Формула свертки Разностное уравнение Рекурсивные и нерекурсивные линейные дискретные системы КИХ- и БИХ-системы Устойчивость линейных дискретных систем Оценка устойчивости по импульсной характеристике Описание линейных дискретных систем в -области Z-преобразование Передаточная функция. Соотношение вход/выход Взаимосвязь между передаточной функцией и разностным уравнением Передаточная функция и импульсная характеристика звена -го порядка Оценка устойчивости по передаточной функции Нули и полюсы передаточной функции звеньев -го порядка37.5. Описание линейных дискретных систем в частотной области Частотная характеристика. Соотношение вход/выход Основные свойства частотных характеристик Расчет АЧХ и ФЧХ Расчет АЧХ и ФЧХ звена -го порядка Экспресс-анализ АЧХ и ФЧХ звена -го порядка Анализ АЧХ по карте нулей и полюсов Основы построения структурных схем Задание на контрольную работу Примеры выполнения контрольной работы Пример 3. Пример Пример Литература Предметный указатель

4 ВВЕДЕНИЕ Цифровая обработка сигналов ЦОС это область науки и техники, в которой изучаются общие для разных дисциплин алгоритмы и средства обработки сигналов средствами цифровой вычислительной техники. Программа дисциплины «Цифровая обработка сигналов» на заочном отделении включает следующие основные темы. Тема. Введение в ЦОС Основные типы сигналов. Типовые дискретные сигналы. Нормирование частоты. Обобщенная система ЦОС. Z-преобразование. Тема. Линейные дискретные системы ЛДС Математическое описание ЛДС во временной области: импульсная характеристика; соотношение вход/выход; формула свертки; разностное уравнение; рекурсивные и нерекурсивные ЛДС; КИХ- и БИХ-системы; определение и критерий устойчивости. Математическое описание ЛДС в -области: передаточная функция; соотношение вход/выход; взаимосвязь передаточной функции с разностным уравнением и импульсной характеристикой; карта нулей и полюсов; оценка устойчивости по передаточной функции. Математическое описание ЛДС в частотной области: частотная характеристика; соотношение вход/выход; свойства частотной характеристики, ее расчет и анализ. Тема 3. Дискретные сигналы Спектр дискретного сигнала и его свойства; связь между спектрами дискретного и аналогового сигналов; дискретное преобразование Фурье ДПФ; быстрое преобразование Фурье БПФ. Тема 4. Введение в цифровые фильтры ЦФ Определение и классификация; основные этапы синтеза ЦФ; задание требований к АЧХ и характеристике ослабления; КИХфильтры с линейной ФЧХ. Тема 5. Синтез ЦФ Синтез оптимальных по Чебышеву КИХ-фильтров; синтез БИХ-фильтров методом билинейного Z-преобразования. Тема 6. Квантование в цифровых системах Источники шумов в цифровых системах; предположение об источниках; детерминированные и вероятностные оценки шумов кван- 4

5 тования; эффекты переполнения в сумматорах; понятие о предельных циклах. Тема 7. Реализация алгоритмов ЦОС Понятие о реальном времени алгоритмов ЦОС и их программной реализации на базе процессоров цифровой обработки сигналов ЦПОС; краткий обзор особенностей архитектуры ЦПОС ведущих на российском рынке фирм-производителей. Данное учебное пособие посвящено изучению темы и разработано на базе курса лекций [], который рекомендуется в качестве основного по дисциплине «Цифровая обработка сигналов». Учебное пособие включает 3 раздела:. Теоретические основы линейных дискретных систем.. Задание на контрольную работу. 3. Типовые примеры выполнения контрольной работы. Приводится список литературы и предметный указатель.. ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ: ОСНОВЫ ТЕОРИИ В этом разделе дается краткая теоретическая справка по анализу линейных дискретных систем и приводится необходимый сопутствующий материал. АНАЛОГОВЫЕ И ДИСКРЕТНЫЕ СИГНАЛЫ. НОРМИРОВАНИЕ ВРЕМЕНИ Сигналом называют физический процесс, несущий в себе информацию. Математически сигналы описываются функциями времени, тип которых зависит от типа сигнала. К основным типам сигналов относят: аналоговый, дискретный, цифровой. Аналоговым называется сигнал, непрерывный во времени и по состоянию рис. а. Такой сигнал описывается непрерывной или кусочно-непрерывной функцией x t, причем и аргумент, и сама функция могут принимать любые значения из некоторых интервалов t t t, x x x соответственно. Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию рис. б. Он описывается решетчатой функцией последовательностью xt, где. Последо- 5

6 вательность xt определена только в моменты времени T и может принимать любые значения из некоторого интервала x x x. Комплексный дискретный сигнал описывается двумя вещественными последовательностями x T x T + jx T. Цифровым называют сигнал, дискретный по времени и квантованный по состоянию. Такой сигнал описывается квантованной решетчатой функцией квантованной последовательностью x ц T, отсчеты которой в каждый момент времени T принимают квантованные значения из некоторого интервала x x x. Интервал T называют периодом дискретизации, а обратную величину fд T. частотой дискретизации. xt а t xt б T T 6 Рис. Примеры аналогового и дискретного сигналов При анализе дискретных сигналов удобно пользоваться нормированным временем

7 откуда при t T t t T t.. T T Таким образом, номер отсчета дискретного сигнала является нормированным временем: иначе говоря, номер означает, что отсчет взят в момент T. Переход к нормированному времени позволяет рассматривать дискретный сигнал как функцию целочисленной переменной. В дальнейшем обозначения дискретного сигнала x и x T будем считать тождественными x T x. Типовые дискретные сигналы При исследовании линейных дискретных систем ряд дискретных сигналов используют в качестве испытательных воздействий; такие сигналы называют типовыми. К ним относятся: Цифровой единичный импульс, описываемый последовательностью, ; u.3,, из чего следует, что этот сигнал равен единице при и нулю при всех остальных значениях рис. а. u u t T, 3 3 а б Рис. Цифровой единичный импульс Задержанный цифровой единичный импульс, описываемый последовательностью 7

8 , ; u.4, из чего следует, что этот сигнал, в отличие от незадержанного, равен единице только при и нулю при всех остальных значениях рис. б. Произвольный дискретный сигнал можно описать в виде суммы m x x m u m,.5 что оказывается удобным при выводе ряда соотношений см п..3.. Подставляя в.5 любое значение, получаем тождество, например, для x при имеем x x u + x u + x u + x3 u +. откуда, с учетом определения цифрового единичного импульса u.3, имеем x x. Дискретная экспонента, описываемая последовательностью x a, ;.6, дискретная экспонента будет убывающей, знакопостоянной рис..3, а; 8

9 при a возрастающей; при a и a > цифровым единичным скачком; при a и a 10 или, при разложении по формуле Эйлера, двумя вещественными последовательностями косинусоидой вещественная часть и синусоидой мнимая часть x Acos ωt + jasi ωt. Основная полоса частот. Нормирование частоты Согласно теореме Котельникова максимальная частота аналогового сигнала f не должна превышать половины частоты дискретизации д в f этого сигнала, следовательно, в частотной области все дискретные сигналы целесообразно рассматривать только в области f д ;, которая называется основной полосой частот или основным диапазоном частот. Это позволяет ввести понятие нормированной частоты f f f T, f или д ω ω f д ωt,.8 в результате чего основная полоса частот станет равной f [;,5] или ω [; π]. Обычно отдается предпочтение абсолютной частоте f и нормированной частоте ω см. также п..4.. Введение нормированной частоты указывает на то, что в ЦОС важны не абсолютные значения частот сигнала и дискретизации, а их отношение. Покажем это на простейшем примере двух дискретных косинусоид: f x cosπft cosπ, f где f Гц, f д 6 Гц; f x cosπf T cosπ, f где f 5кГц, f д 4 кгц. д д

11 Подставив указанные значения частот, получим одинаковые дискретные сигналы в шкале нормированной частоты ω : x cos π cos 6 4 ; 5 x cos π cos ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ Системой обработки сигналов системой называют объект, выполняющий требуемое преобразование обработку входного сигнала в выходной. Системой может быть как физическое устройство, так и математическое преобразование. По умолчанию будем подразумевать системы с одним входом и одним выходом. Входной сигнал называют воздействием, выходной реакцией. Систему называют линейной, если она обладает свойствами: — аддитивности: реакция на сумму воздействий равна сумме реакций на каждое из воздействий принцип суперпозиции; — однородности: умножению воздействия на весовой коэффициент соответствует реакция, умноженная на тот же коэффициент. Соотношение вход/выход линейной системы описывается линейным уравнением. Систему называют стационарной, если она обладает свойством инвариантности во времени, в соответствии с которым задержка воздействия на некоторое время приводит к задержке реакции на то же время. Параметры стационарной системы неизменны во времени. По умолчанию будем подразумевать стационарные системы. Линейная система называется дискретной, если воздействие и реакция представляют собой дискретные сигналы x T и y T рис..5. x T yt ЛДС Воздействие Реакция Рис..5. Линейная дискретная система Начальные условия дискретной системы могут быть нулевыми или ненулевыми. Признаком нулевых начальных условий является отсутствие реакции y T при отсутствии воздействия x T.

12 Обозначив начальный момент времени, нулевые начальные условия можно записать в следующем общем виде: x[ i T ] i , но не зависят от его по- значений воздействия x [ m T ] следующих значений x [ m T ] +, m. Условия физической реализуемости отображают причинноследственную связь принцип причинности. Линейные дискретные системы ЛДС помимо временной области описываются в -области и в частотной области. В каждой из этих областей для ЛДС определяется: — основная характеристика; — соотношение вход/выход..3. ОПИСАНИЕ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ ВО ВРЕМЕННОЙ ОБЛАСТИ Во временной области основной характеристикой ЛДС является импульсная характеристика. Импульсной характеристикой ИХ h T ЛДС называется ее реакция на цифровой единичный импульс u T при нулевых начальных условиях рис..6. x T u T y T h T ЛДС Рис..6. К определению импульсной характеристики

13 Соотношение вход/выход ЛДС отображает взаимосвязь между ее входным x T и выходным y T сигналами, т. е. реакцию ЛДС на произвольное воздействие. Во временной области соотношение вход/выход может описываться одним из двух разновидностей линейных уравнений: — формулой свертки название уравнения, если для определения реакции используется импульсная характеристика; — разностным уравнением, если для определения реакции используются параметры ЛДС см. п Формула свертки Получим уравнение взаимосвязи между входным x T и выходным y T сигналами для ЛДС, заданной своей импульсной характеристикой h T. Воспользуемся определением ИХ и свойствами ЛДС. Будем последовательно записывать соответствия, указываемые стрелкой, между воздействием и реакцией: — по определению: воздействию в виде цифрового единичного импульса соответствует реакция, называемая импульсной характеристикой u T h T ; — на основании свойства инвариантности во времени для стационарных линейных систем: воздействию, задержанному на время mt, где m cost, соответствует реакция, задержанная на то же время u T mt h T mt ; — на основании свойства однородности линейных систем: умножению воздействия на весовой коэффициент константу x mt соответствует реакция, умноженная на тот же коэффициент u T mt x mt h T mt x mt ; — на основании свойства аддитивности линейных систем: реакция на сумму воздействий равна сумме реакций на каждое из воздействий m u T mt x mt h T mt x mt ; m — слева имеем воздействие в виде суммы.5 3

14 а справа реакцию xt u T mt x mt, m 4 m y T h T mt x mt,. где h T mt импульсная характеристика, задержанная на m периодов дискретизации. Линейное уравнение. называют формулой свертки, согласно которой реакция y T вычисляется как дискретная свертка воздействия xt и импульсной характеристики h T. Выполнив замену переменных в., можно получить другой вариант записи формулы свертки m y T h mt x T mt.. Для нормированного времени формула свертки в двух вариантах записи. и. принимает вид соответственно m y h m x m ;. m y h m x m..3 Выбор варианта формулы свертки определяется удобством применения в конкретном случае. Линейная дискретная система, соотношение вход/выход которой описывается в виде формулы свертки, отвечает условиям физической реализуемости: при нулевых начальных условиях.9 x m m 15 Пример.. Вычислить реакцию ЛДС по формуле свертки. Импульсная характеристика и воздействие заданы графически рис Требуется определить восемь отсчетов реакции. h x Рис..7. Импульсная характеристика Рис..8. Воздействие Решение приведено в табл. а график вычисленной реакции на рис..9. Таблица. Вычисление реакции по формуле свертки Реакция y y hx + hx + hx + hx y hx + hx + hx + hx + hx + 5 y hx + hx + hx + h3x + hx + hx + hx y3 hx3 + hx + hx + h3x + h4x + hx3 + +hx + hx + h3x y4 hx4 + hx3 + hx + h3x + h4x + h5x + hx4 + hx3 + hx + h3x + h4x y5 hx5 + hx4 + hx3 + h3x + h4x + h5x + + h6x + hx5 + hx4 + hx3 + h3x + h4x + h5x y6 7 y7 y Рис..9. Реакция 5

16 .3.. Разностное уравнение Взаимосвязь между воздействием x T и реакцией y T соотношение вход/выход может описываться разностным уравнением РУ N M [ i T ] ak y[ k T ] y b x,.4 i i где b i, a k коэффициенты уравнения вещественные константы; x T, y T воздействие и реакция вещественные или комплексные сигналы; i, k значения задержек воздействия и реакции соответственно; N, M константы; x [ i T ], y[ k T ] воздействие и реакция, задержанные на i и k периодов дискретизации соответственно. Коэффициенты b i и a k называются внутренними параметрами параметрами ЛДС. Для нормированного времени разностное уравнение.4 принимает вид N k M y b x i a y k..5 i i k k Линейная дискретная система, соотношение вход/выход которой описывается в виде разностного уравнения.5, отвечает условиям физической реализуемости: при нулевых начальных условиях.9 реакция не может возникнуть раньше воздействия; значения реакции в каждый момент времени зависят только от текущего и предшествующих значений воздействия, но не зависят от его последующих значений см. п..3. Разностное уравнение.5 решается методом прямой подстановки при нулевых начальных условиях.9, следовательно, оно непосредственно описывает алгоритм вычисления реакции по известному воздействию и параметрам ЛДС. Пример.. Решить разностное уравнение y x,5y методом прямой подстановки при заданном воздействии и нулевых начальных условиях 6

17 x,. Требуется определить 5 отсчетов реакции. Решение приведено в табл. Таблица. Вычисление реакции методом прямой подстановки Воздействие Реакция x y x,5y,5 x, y x,5y,,5,,5,4 x, y x,5y,,5,4, +,, 3 x3, y3 x3,5y,,5. 5,4 4 x4, y4 x4,5y3,,5,4,+,5,5 M M M.3.3. Рекурсивные и нерекурсивные линейные дискретные системы Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентов a k разностного уравнения.5 не равен нулю: a k хотя бы для одного из значений k. Порядком рекурсивной ЛДС называют порядок РУ.5, т. е. max< M, N >. Согласно.5 реакция y рекурсивной ЛДС в каждый момент времени определяется: — текущим отсчетом воздействия x; — предысторией воздействия x i, i. N ; — предысторией реакции y k, k. M. Примеры разностных уравнений рекурсивной ЛДС: — первого порядка y b x + bx a y ;.6 — второго порядка y b x + b x + b x a y a y..7 Линейная дискретная система называется нерекурсивной, если все коэффициенты a k разностного уравнения.5 равны нулю: a, k. M. k 7

18 Для нерекурсивной ЛДС разностные уравнения.4.5 принимают вид соответственно 8 N bi i N bi i [ i T ] y x ;.8 y x i..9 Порядок нерекурсивной ЛДС равен N. Согласно РУ.9 реакция y нерекурсивной ЛДС в каждый момент времени определяется: — текущим отсчетом воздействия x ; — предысторией воздействия x i, i. N. Пример РУ нерекурсивной ЛДС второго порядка: y b x + b x + b x КИХ- и БИХ-системы Рассмотрим особенности импульсных характеристик рекурсивных и нерекурсивных ЛДС. С этой целью приведем примеры вычисления ИХ по заданному разностному уравнению, решая его методом прямой подстановки при нулевых начальных условиях. Пример.3. Вычислить импульсную характеристику нерекурсивной ЛДС второго порядка, соотношение вход/выход которой описывается разностным уравнением.: y b x + b x + b x. Решение. Согласно определению ИХ это реакция на цифровой единичный импульс рис..6, поэтому, выполнив замену x u ;. y h, перепишем РУ в виде h bu + bu + bu и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях см. п..3.: h b u + b u + b u b + b + b b ; bu + bu + bu b + b + b bu + bu + bu b + b + b h b ; h b ;

19 h 3 b u 3 + bu + bu b + b + b ; h при > 3. Распространяя полученные результаты на ИХ нерекурсивной ЛДС произвольного порядка, можно сделать следующие выводы: — импульсная характеристика нерекурсивной ЛДС имеет конечную длительность; — значения отсчетов ИХ равны коэффициентам разностного уравнения h b i, при i. N. Поэтому нерекурсивные ЛДС называют системами с конечной импульсной характеристикой КИХ-системами. Пример.4. Вычислить импульсную характеристику рекурсивной ЛДС первого порядка, соотношение вход/выход которой описывается разностным уравнением y b x a y. Решение. Выполнив замену., перепишем РУ в виде h bu ah и вычислим отсчеты ИХ методом прямой подстановки при нулевых начальных условиях: h b u a h b ; u ah h b a b ; u ah a ab u 3 ah a a b 3 a h b a b ; h 3 b b. M Вычисления можно продолжать бесконечно по формуле h a b, 4, 5. Распространяя полученные результаты на ИХ рекурсивной ЛДС произвольного порядка, можно сделать вывод: импульсная характеристика рекурсивной ЛДС имеет бесконечную длительность. Поэтому рекурсивные ЛДС называют системами с бесконечной импульсной характеристикой БИХ-системами Устойчивость линейных дискретных систем ЛДС называется устойчивой, если при ограниченном воздействии 9

20 max x R, где R x любое, сколь угодно большое положительное число, не равное бесконечности, и произвольных, но ограниченных начальных условиях реакция также ограничена max y R, где y R любое сколь угодно большое положительное число, не равное бесконечности Оценка устойчивости по импульсной характеристике Существуют два критерия устойчивости ЛДС. Один из них позволяет оценить устойчивость ЛДС по ее импульсной характеристике во временной области, другой по -изображению этой характеристики в -области см. п..4. Выбор критерия зависит от удобства его практического использования. Критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике, формулируется следующим образом: для того чтобы ЛДС была устойчива, необходимо и достаточно выполнения условия абсолютной сходимости ряда x y h 21 представляющий собой сумму бесконечной геометрической прогрессии q, q a. Как известно, сумма такого ряда в области сходимости, т. е. при a 22 — обеспечить автоматический переход к частотным характеристикам и многое другое. Прежде чем перейти к описанию ЛДС в -области, рассмотрим математический аппарат Z-преобразования..4.. Z-преобразование В данном разделе приводятся необходимые для дальнейшего рассмотрения сведения о математическом аппарате Z-преобразования. Более подробная информация содержится в []. Z-преобразованием прямым последовательности x T называют следующий ряд < x >X Z x T,. где x T оригинал вещественная или комплексная последовательность, для которой выполняется условие.9; X -изображение последовательности x T, результат Z- преобразования. Z-преобразование однозначно связано с последовательностью x T и справедливо только в области абсолютной сходимости ряда x T 23 T [ cos ωt + j si ωt ] σ, имеем вещественную ξ и мнимую j η части комплексной переменной рис. σ ξ T cos ωt ;.7 σ η T si ωt..8 Комплексная переменная может быть представлена в двух формах: — алгебраической ξ + jη ;.9 — показательной jϕ r,.3 где радиус r является модулем, а угол ϕ аргументом переменной.9: r ξ + η ;.3 η ξ ϕ arg arctg /..3 Рис. Комплексные p- и -плоскости Соответственно, положение произвольной точки на комплексной -плоскости может указываться: — координатами ξ;η в декартовой системе координат; — полярными координатами радиусом r и углом ϕ в полярной системе координат. Сопоставляя соотношения.6 и.3, выразим значения радиуса r и угла ϕ через σ и ω соответственно: σt r ;.33 3

24 ϕ ωt ω..34 Равенство.34 указывает на то, что угол ϕ точки на комплексной -плоскости есть не что иное, как нормированная частота ω.8, измеряемая в радианах. j ω± πk В силу периодичности экспоненты угол ϕ.34 комплексной переменной определяется с точностью до слагаемого πk, где k любое целое число: ϕ ω ± πk ω ± πk, однако, как правило, по умолчанию речь идет о главном значении аргумента из диапазона π 25 . Точка p-плоскости с координатами σ ; ω соответствует началу координат -плоскости точке с координатами ξ ; η : pt j T. 3. Точка p-плоскости на оси частот jω с координатами σ ; ω π / T отображается в точку -плоскости с координатами ξ ; η ; в полярных координатах r ; ϕ π/, рис. табл..3: π π j T j pt T T cos + j si j. 4. Точка p-плоскости на оси jω с координатами σ ; ω π / T отображается в точку -плоскости с координатами ξ ; η ; в полярных координатах r ; ϕ π/, рис. табл..3: π π j T j pt T T cos + j si j. 5. Две точки p-плоскости на оси jω с координатами σ ; ω ±π / T отображаются в одну точку -плоскости с координатами ξ ; η ; в полярных координатах r ; ϕ ±π, рис. табл..3: pt T ± π j T T ± jπ cos ± π + j si ± π j 6. Отрезок оси частот jω p-плоскости π π π σ ; 26 j ω : πk k ωд, k. отображается на -плоскости в k совпадаю- T щих единичных окружностей π 27 π π π σ ; ; ; π 28 Таблица.3 Отображение p-плоскости на -плоскость p-плоскость -плоскость p σ + jω ξ + jη r jϕ σ ω ξ η r ϕ ω 3 π π T 4 π π T 5 π T π 6 π T π 7 Отрезок мнимой оси Единичная окружность один оборот π π π π π отсчетов, равно -изображению незадержанной последовательности, умноженному на m, т. е. если Z < x T >X, то 8

29 m < x[ m T ]>X Z. Теорема о свертке: -изображение свертки последовательностей x T и x T x T x mt x[ m T ] m равно произведению -изображений свертываемых последовательностей Z < x T >X X X. В приведенных выше свойствах -изображение вычисляется по формуле прямого Z-преобразования.. Обратное Z-преобразование Обратное Z-преобразование определяется соотношением < >Z X x T X d, πj где Z < X >символическое обозначение обратного Z-преобразования; С любой замкнутый контур в области сходимости подынтегральной функции, охватывающий все ее особые точки см. п..4. и начало координат комплексной -плоскости. Существуют упрощенные способы вычисления обратного Z- преобразования, заменяющие непосредственное сложное вычисление интеграла по замкнутому контуру; наиболее простой из них основан на использовании таблицы соответствий табл..4, где последовательности представлены в нормированном времени см. п. Поясним правило пользования табл..4 на примерах. Пример.6. Известно -изображение, +,5 X.,8 Требуется найти оригинал x. Решение. Представим дробно-рациональную функцию X в виде суммы C 9

30 3 Таблица.4 Таблица соответствий Последовательность x -изображение X,, u U > a a x + a X 3 > a a x a X 4 [ ] ϕ ϕ + si si r x + + a a X, где cos ϕ r a r a,8,5,8,,8,5,8, X X X и, пользуясь свойством линейности Z-преобразования, определим оригинал x как сумму обратных Z-преобразований: < > < > < >x x X Z X Z X Z x + +. Оригинал < >,8,,8, Z Z X Z x, согласно табл..4 столбец 3 при 8, a, а также свойству линейности Z-преобразования равен x 8. 39 Оригинал < >,8,5,8,5 Z Z X Z x

31 согласно табл..4, столбец 3 при a, 8, а также свойству линейности Z- преобразования и теореме о задержке равен,5, 8 x. Искомый оригинал равен сумме последовательностей x и x : + x,,8 +,5, 8 x x..4 С учетом нулевых начальных условий оригинал x определяется следующим образом. 8, ; x.,8 +,5,8, >, поскольку при значение x определяется в области отрицательного времени и, следовательно, при нулевых начальных условиях x,5, Передаточная функция. Соотношение вход/выход Основной характеристикой ЛДС в -области является -изображение импульсной характеристики h < h >H Z,.4 которое определяется по формуле прямого Z-преобразования. H h..4 При известном -изображении H импульсная характеристика h находится с помощью обратного Z-преобразования < H >h Z,.43 где H называют передаточной функцией ПФ ЛДС; это математическое определение ПФ. Соотношение вход/выход ЛДС во временной области описывалось с помощью формулы свертки, либо в виде разностного уравнения. Рассмотрим поочередно их отображение в -области. Формуле свертки см. п..3. 3

32 h m x m; y m x m h m, m в -области соответствует уравнение см. п..4. Y H X,.44 где X и Y -изображения воздействия и реакции. На основании.44 передаточную функцию можно представить как отношение Y H,.45 X которое позволяет ее определить подобно передаточной функции линейных аналоговых систем. Передаточной функцией H ЛДС называется отношение -изображения реакции к -изображению воздействия при нулевых начальных условиях. Данное определение ПФ не противоречит приведенному математическому.4. Действительно, согласно определению, импульсная характеристика h есть реакция на воздействие в виде цифрового единичного импульса u. Подставив -изображения данных воздействия и реакции в.45 и учитывая, что Z < u >см. табл..4, получим определение ПФ.4: Y Z < h >H Z< h >. X Z < u >Разностному уравнению.5 y N i i b x i M k k a y k в -области соответствует уравнение, которое можно получить, выполнив Z-преобразование правой и левой частей РУ: N M Z < y >Z bi x i ak y k. i k 3

33 Используя свойства Z-преобразования линейность и теорему о задержке, запишем N i i i M k k Y X b Y a, откуда после приведения подобных имеем алгебраическое уравнение N bi i Y X..45а M k + a k Разделив обе части этого уравнения на X, получим передаточную функцию общего вида i k N i bi i M k ak k H ПФ.46 представляет собой дробно-рациональную функцию, числитель и знаменатель которой являются многочленами относительно порядков N и M соответственно с вещественными коэффициентами b i и a k. Следовательно, ПФ зависит исключительно от внутренних параметров ЛДС см. п..3. и не зависит ни от воздействия, ни от реакции. Порядком ПФ называют наибольшее из чисел N и M. Здесь и далее полагаем, что порядок многочлена числителя не превосходит порядка многочлена знаменателя: N M. Передаточные функции -го и -го порядков описывают простейшие ЛДС, называемые звеньями -го и -го порядков соответственно. Как любая дробно-рациональная функция, ПФ.46 характеризуется своими особыми точками полюсами и нулями. Нулями ПФ называют значения, при которых H оказывается равной нулю. Особыми точками полюсами ПФ называют значения, при которых знаменатель H оказывается равным нулю []. k 33

34 Картой нулей и полюсов называют изображение координат нулей кружочками и полюсов звездочками * на комплексной — плоскости. Как будет показано см. пп , такая карта является весьма важной графической характеристикой ЛДС Взаимосвязь передаточной функции и разностного уравнения Из сравнения передаточной функции.46 и соответствующего ей разностного уравнения.5 легко видеть, что: — многочлен числителя ПФ связан с отсчетами воздействия b i x i ; при этом величина задержки i отсчета x i отображается степенью, а коэффициенты b i остаются неизменным; символически это соответствие можно записать следующим образом: 34 i i i bi x i b, i. N ; — многочлен знаменателя ПФ связан с отсчетами реакции y и a k y k, при этом свободный член всегда равен : a, так как в РУ он соответствует реакции y см. п..4.; величина задержки k отсчета y k отображается степенью коэффициенты a k меняют знак; символически это соответствие можно записать следующим образом: k k k a y k a. Пример.7. Дана передаточная функция общего вида. Записать соответствующее ей разностное уравнение: — для звена -го порядка числитель и знаменатель ПФ многочлены -го порядка: передаточной функции b b + H.47 + a соответствует разностное уравнение y b x + b x a y ;.48 — для звена -го порядка числитель и знаменатель ПФ многочлены -го порядка: k, а

35 передаточной функции b + b + b H.49 + a + a соответствует разностное уравнение y b x + b x + bx a y ay..5 Звено называют базовым, если числитель его передаточной функции равен. ПФ базовых звеньев -го и -го порядков имеют вид соответственно: H ; H + a +. a + a.4.4. Передаточная функция и импульсная характеристика звена -го порядка Упрощенная методика определения импульсной характеристики h по заданной передаточной функции H предполагает, что взаимосвязь между ИХ и ПФ базовых звеньев известна из таблицы соответствий см. табл..4, в предположении, что: X передаточная функция H базового звена; x импульсная характеристика h базового звена. Следовательно, передаточной функции базового звена -го порядка H + a соответствует импульсная характеристика h a, а передаточной функции базового -го порядка H + a + a соответствует импульсная характеристика si[ + ϕ] h r,.5 si ϕ где r и ϕ радиус и угол комплексно-сопряженных полюсов, ± jϕ * r..5 35

36 Значения r и ϕ * и a и a связаны между собой соотношениями см. табл r a ;.53 a r cos ϕ..54 Напомним см. рис. что угол полюса ϕ есть нормированная частота ω. Здесь и в дальнейшем будем использовать индексы звездочка и кружок для обозначения полюса и нуля соответственно. Для записи ИХ небазового звена -го порядка достаточно воспользоваться свойствами линейности Z-преобразования и теоремой о задержке. Тогда передаточной функции небазового звена -го порядка b + b + b H + a + a будет соответствовать импульсная характеристика небазового звена -го порядка si[ + ϕ] si ϕ si[ ϕ] h br + br + br si ϕ si ϕ si ϕ.55 или с учетом нулевых начальных условий b r h b r b r si si si [ + ϕ ] si ϕ [ + ϕ ] si ϕ ; + b r [ + ϕ ] si ϕ si [ ϕ ] si ϕ, + b r si ϕ si ϕ si ϕ, ; + b r si ϕ.56, Оценка устойчивости по передаточной функции В п..3.6 при описании ЛДС во временной области рассмотрен критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике. В -области, где основной характеристикой ЛДС является передаточная функция -изображение ИХ, сущест-

37 вует критерий, позволяющий оценить устойчивость ЛДС по передаточной функции, а именно: для того чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюсы ее передаточной функции располагались внутри единичного круга комплексной — плоскости 38 Если нули комплексно-сопряженные o, ξ o + jη o, их следует представить в показательной форме 38 ± jϕo o, r o,.6 где радиус r o и угол ϕ o определяются из.3 и.3 соответственно: η r o ξ o + η o ; ϕ o o arctg. ξ o Если коэффициент b, то вычисление комплексно-сопряженных нулей можно упростить: не умножая числитель и знаменатель ПФ.47 на, определять нули в виде.6, где r и ϕ рассчитываются по формулам подобным.53.54, а именно: r o b ; b r cos ϕ..5. ОПИСАНИЕ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ В ЧАСТОТНОЙ ОБЛАСТИ В разд..3 рассматривалось описание ЛДС во временной области: импульсная характеристика и соотношение вход/выход в виде формулы свертки либо разностного уравнения. Здесь рассматривается их отображение в частотной области. Описание ЛДС в частотной области позволяет: — ввести фундаментальное для теории линейных систем понятие частотной характеристики; при проектировании большинства систем ЦОС именно к частотным характеристикам предъявляются и выдерживаются требования; — определять реакцию ЛДС в установившемся режиме не только на гармоническое воздействие, но и на любое воздействие, которое можно представить как линейную комбинацию гармонических воздействий..5.. Частотная характеристика. Соотношение вход/выход Основной характеристикой ЛДС в частотной области является фурье-изображение импульсной характеристики h T, которое определяется по формуле прямого преобразования Фурье

39 39 ω ω T j T j T h H,.6 или для нормированных частоты и времени: ω ω j j h H..6 При известном фурье-изображении T j H ω импульсная характеристика T h находится с помощью обратного преобразования Фурье ω π ω π π ω d H T T h T j T T T j, где ω ω j T j H H называют комплексной частотной характеристикой КЧХ или коротко частотной характеристикой ЧХ; это математическое определение ЧХ. Определим ЧХ подобно тому, как это делается для линейных аналоговых систем, относительно которых известно, что гармоническое воздействие вызывает гармоническую реакцию той же частоты, но в общем случае другой амплитуды и начальной фазы. Рассмотрим реакцию ЛДС на дискретное комплексное гармоническое воздействие ω ϕ ω x j x j x C C x.63 с амплитудой и фазой соответственно cost x C ; x ω ω ϕ. Для вычисления реакции воспользуемся формулой свертки.3, ω ω ω ω m m j m m m j j x m j x m m h x m h C m C h m x m h y откуда с учетом определения ЧХ.6 ω j H x y.

40 На основании этого частотную характеристику можно представить как отношение ω y.64 x H j x C jω и определить следующим образом. jω Частотной характеристикой ЧХ H ЛДС называется частотная зависимость отношения реакции к дискретному гармоническому воздействию в установившемся режиме. Подчеркнем, что отношение.64 справедливо исключительно для гармонического воздействия и установившегося режима работы ЛДС. Поясним, смысл «установившегося режима». Теоретически, область изменения гармонического воздействия 41 jω jϕ ω x y x H C x A ω j[ ϕ ω +ϕ ω ] C A ω x C x y jϕy ω jϕ ω,.68 откуда следует, что реакция на комплексный гармонический сигнал есть тоже комплексный гармонический сигнал той же частоты, что и воздействие, но с частотно-зависимыми амплитудой C C Aω и фазой ϕ y x ω ϕ ω + ϕ ω y x. Сопоставив выражения для реакции.68 и воздействия.63, дадим определения АЧХ и ФЧХ. Амплитудно-частотной характеристикой ЛДС A ω называется частотная зависимость отношения амплитуды реакции к амплитуде дискретного гармонического воздействия в установившемся режиме: C y Cx A ω A ω. Cx C x Фазочастотной характеристикой ЛДС ϕ ω называется частотная зависимость разности фаз реакции и дискретного гармонического воздействия в установившемся режиме: ϕ ω ϕ ω ϕ ω + ϕ ω ϕ ω ϕ ω [ ] y x x x. Связь частотной характеристики с передаточной функцией Сравним передаточную функцию.4 с частотной характеристикой.6, взаимосвязь которых очевидна: jω jω ω H j H,.69 jω т. е. ЧХ H совпадает с ПФ H, если область значений переменной на комплексной -плоскости ограничена точками на jω единичной окружности. Это позволяет при известной передаточной функции путем подстановки автоматически получать частотную характеристику, а от известных соотношений вход/выход.44,.45а в — области: 4

42 4 X H Y ; X a b Y M k k k N i i i + автоматически перейти к соответствующим соотношениям в частотной области: ω ω ω j j j X H Y ; ω ω ω ω + j M k jk k N i ji i j X a b Y, где T j j X X ω ω ; T j j Y Y ω ω фурье-изображения воздействия и реакции соответственно. На основании этого частотную характеристику можно определить как отношение фурье-изображений реакции и воздействия при нулевых начальных условиях, подобно передаточной функции.45 при подстановке ω j : ω ω ω ω j j j X Y X Y H j..5.. Основные свойства частотных характеристик. ЧХ T j H ω, АЧХ ω A и ФЧХ ω ϕ непрерывные функции частоты по определению.. ЧХ T j H ω, АЧХ ω A и ФЧХ ω ϕ периодические функции частоты с периодом, равным частоте дискретизации T π ω д. Доказательство периодичности функций следует из того, что их аргумент T j ω периодическая функция частоты с периодом T π

43 jωt πk j ω± T T jωt jπk. В зависимости от используемой шкалы частот период ЧХ, АЧХ и ФЧХ равен f f д ;.7 ω ω д ;.7 ω π..7 Если коэффициенты ПФ вещественные а другие не рассматриваются, то АЧХ будет четной, а ФЧХ нечетной функцией частоты []: A ω A ω ; ϕ ω ϕ ω. Напомним, что четной называется такая функция, которая не изменяет своего значения при изменении знака переменной. Если же при изменении знака переменной изменяется знак функции, а ее абсолютное значение сохраняется неизменным, то такая функция называется нечетной. На практике представляют интерес графики АЧХ и ФЧХ в основной полосе частот см. п Расчет АЧХ и ФЧХ Получим частотную характеристику H ω по известной передаточной функции H общего вида.46 Выполнив замену N k i bi i H. M k + a,.73 запишем частотную характеристику в виде N k k jωt j iωt j jωt bi jωt i H..74 M j kωt + a k T 43

44 Раскроем экспоненты по формуле Эйлера, например, в знаменателе cos kωt j si kωt,.75 после чего выделим вещественные и мнимые части в числителе и знаменателе.74: jωt R ч + j Imч H,.76 R з + j Imз где индексы «ч» и «з» означают числитель и знаменатель. Определим модуль АЧХ и аргумент ФЧХ частотной характеристики H 44 j ω T jkωt ч з ч з jωt R + Im A ω H ;.77 R + Im jωt Imч Imз < >arctg arctg Rч Rз ϕ ω arg H..78 Полученные выражения используются для расчета АЧХ и ФЧХ в основной полосе частот Расчет АЧХ и ФЧХ звена -го порядка Пользуясь описанной выше методикой, определим АЧХ и ФЧХ звена -го порядка по его передаточной функции H.49: b b + + b H. + a + a Выполнив замену переменных.73 и используя нормированную частоту ω ωt, получим частотную характеристику jω jω jω b + b + b jω jω + a + a H..79 Раскрыв экспоненты по формуле Эйлера.75 ω b + b [ cos ω j si ω ] + b[ cosω j siω ] H j + a[ cos ω j siω ] + a[ cos ω j siω ] и выделив вещественные и мнимые части согласно.76, запишем частотную характеристику в виде ω [ b + b cos ω + b cosω ] j[ b si ω + b siω ] H j..8 + a cos ω + a cosω j a si ω + a siω [ ] [ ]

45 jω Модуль АЧХ данной H согласно.77 равен [ b + b cos ω + b cosω ] + [ b si ω + b siω ] A ω,.8 [ + a ] [ ] cos ω + a cosω + a si ω + a siω аргумент ФЧХ согласно.78 равен a si ω + a siω ϕ ω arctg + a cos ω + a cosω..8 b si ω + b siω arctg b + b cos ω + b cosω Особенности расчета по данным формулам обсуждаются ниже Экспресс-анализ АЧХ и ФЧХ звена -го порядка На практике часто требуется оценить АЧХ и ФЧХ при минимуме расчетов. С этой целью строят приближенные графики рассматриваемых характеристик по их значениям в нескольких точках, количество которых должно быть минимально достаточным. Такой быстрый способ оценки частотных характеристик называется экспресс-анализом. Экспресс-анализ АЧХ предполагает заранее известными особенности анализируемой функции: гладкость, количество экстремумов, нулей и др. Проведем экспресс-анализ АЧХ и ФЧХ звена -го порядка. Методами математического анализа можно показать, что в основной полосе частот АЧХ звена -го порядка.8: — имеет экстремум либо нуль на границах основной полосы, при этом нуль будет наименьшим значением, но не минимумом АЧХ; — может иметь один максимум и один минимум либо нуль внутри основной полосы, при этом нуль будет наименьшим значением, но не минимумом АЧХ. При отсутствии нулей АЧХ представляет собой гладкую функцию. Следовательно, для оценки АЧХ звена -го порядка достаточно построить ее график по пяти точкам: — двум на границах основной полосы, — одной уточняющей посередине основной полосы, — двум внутри основной полосы, соответствующим максимуму и минимуму либо нулю АЧХ. 45

46 Полагая, что передаточная функция H.49 звена -го порядка известна, получим формулы экспресс-анализа АЧХ и ФЧХ по следующим пяти точкам π ω ; π; ; ω ; ω o, где ω частота, на которой АЧХ имеет максимум внутри основной полосы частота максимума АЧХ; ω o частота, на которой АЧХ имеет минимум или равна нулю внутри основной полосы частота минимума или нуля АЧХ. Определим значения АЧХ и ФЧХ в указанных пяти точках: в точке ω рис..5 откуда j ;, b + b + b A H ;.83 + a + a < >ϕ arg H ;.84 j Im j R откуда j Рис..5. Соответствие значений ω и в точке ω π рис..6 jπ ;, b b + b A π H ;.85 a + a < >ϕ π arg H ;.86 46

47 j Im j R j откуда Рис..6. Соответствие значений ω π и π 3 в точке ω рис..7 π j j ; j, b b b jb b + A H j a ja a + a ϕ arg < H j >a arctg a b b jb arg a ja b arctg b b j Im j R. b ; j π Рис..7. Соответствие значений ω и j 4 точка ω ω который находится приблизительно на частоте определяет местоположение максимума АЧХ, ± jϕ r, ; ϕ полюса [] 47

48 ω ϕ ;.89 значение АЧХ в этой точке вычисляется по общей формуле.8; 5 точка ω ω o определяет местоположение минимума АЧХ, который находится приблизительно на частоте ϕ o нуля передаточной функции при значении r o [] 48 ± jϕ r o, ; o o ω o ϕ o, r o ;.9 значение минимума АЧХ в точке ω o вычисляется по общей формуле.8; если в точке ϕ значение r, имеем не минимум, а нуль АЧХ и o o соответственно скачок ФЧХ на π. Строго говоря, на местоположение максимума АЧХ влияют не только полюсы, но и нули, так же, как на местоположение минимума АЧХ влияют не только нули, но и полюсы. Тем не менее доминирующее влияние на местоположение максимума оказывают полюсы, а на местоположение минимума нули, что и отражается символом приблизительного равенства в.89.9 [] Анализ АЧХ по карте нулей и полюсов Как уже говорилось, карта нулей и полюсов является одной из важнейших графических характеристик ЛДС. Помимо оценки устойчивости ЛДС, она позволяет по расположению нулей и полюсов сделать вывод о качественном характере АЧХ. Ниже сформулированы наиболее общие закономерности качественного анализа АЧХ по карте нулей и полюсов в основной полосе частот для звена -го порядка: — передаточная функция звена -го порядка имеет два комплексно-сопряженных или два вещественных полюса, в первом случае максимум АЧХ находится внутри основного диапазона, во втором на его границах два максимума; — передаточная функция звена -го порядка имеет два комплексно-сопряженных или два вещественных нуля, в первом случае минимум или нуль АЧХ находится внутри основной полосы частот, во втором на его границах;

Дайте определение рекурсивных и нерекурсивных ЛДС.

Что такое период и частота дискретизации и как они связаны друг с другом?

=При цифровой обработке сигналов осуществляют выборку значений аналогового сигнала через равные интервалы времени T. Данный процесс называется дискретизацией сигнала по времени. Время T называют периодом дискретизации, а величину обратно пропорциональную F=1/T – частотой дискретизации.

Дайте определение дискретного нормированного времени.

n=nT/T – дискретное нормированное время

4. Дайте определение нормированной частоты .

5. Назовите основные характеристики детерминированных дискретных сигналов,

=В качестве основных параметров сигнала в системах связи используют длительность сигнала, его динамический диапазон и ширину спектра. Под длительностью сигнала Тc

,

где – задержка последовательности.

14 Поясните, как в формуле свертки учитываются ННУ.

В отличие от линейных аналоговых систем, где соответствующие соотношения вод, выход имеют вид интеграла свертки или линейного дифференциального уравнения, вычисление реакции по формуле свертки или РУ выполняется методом прямой подстановки при ННУ, т. е. эти соотношения непосредственно описывают алгоритмы вычисления реакции.

Запишите РУ общего вида.

Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой в z-области – передаточной функцией, имеет вид линейного математического преобразования в виде разностного уравнения

где , – вещественные коэффициенты РУ – параметры ЛДС; i, k – значения задержек воздействия и реакции; , – константы, определяющие максимальные задержки.

Поясните, как в РУ учитываются ННУ.

В отличие от линейных аналоговых систем, где соответствующие соотношения вод, выход имеют вид интеграла свертки или линейного дифференциального уравнения, вычисление реакции по формуле свертки или РУ выполняется методом прямой подстановки при ННУ, т. е. эти соотношения непосредственно описывают алгоритмы вычисления реакции.

Дайте определение рекурсивных и нерекурсивных ЛДС.

рекурсивная ЛДС, реакция которой зависит от текущего и предшествующих отсчетов воздействия и предшествующих отсчетов реакции, т. е.:

хотя бы для одного значения k;

нерекурсивная ЛДС, реакция которой зависит только от текущего и предшествующих отсчетов воздействия, т. е.:

для всех k.