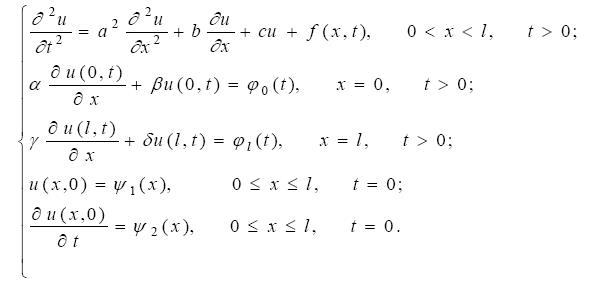Постановка задачи для уравнения параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). Как отмечалось выше, в одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид:
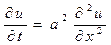
Уравнение (15), например, может описывать распространение тепла в тонком стержне длиной l, теплоизолированном по боковой поверхности. При этом функция u(x, t) задаёт значение температуры в любой точке стержня в произвольный момент времени t, при условии, что известно распределение температуры в стержне в начальный момент времени t = 0 и известна температура на концах стержня x = 0 и x = l в любой момент времени t. Таким образом, постановка задач для уравнения теплопроводности имеет следующий вид.
Первая начально-краевая задача. Если на границах стержня x = 0 и x = l заданы краевые условия первого рода, т.е. для любых моментов времени на концах стержня x = 0 и x = l заданы значения искомой функции u(x,t) (т.е. температуры):
и, кроме того, для функции u(x, t) заданы начальные условия, т.е. задано распределение температуры в любой точке стержня в момент времени t = 0:
то задачу (15) – (17) называют первой начально-краевой задачей для уравнения теплопроводности.
В терминах теории теплообмена функция u(x,t) описывает распределение температуры в пространственно-временной области W´T = <0 £ x £ l, 0 £ t £ T>, параметр а 2 – является коэффициентом температуропроводности, а краевые условия (16), (17) с помощью функций j 1(t) и j 2(t) задают температуру на границах
x = 0, x = l для различных моментов времени.
Вторая начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия второго рода, т.е. для x = 0 и x = l заданы значения производных искомой функции по пространственной переменной:
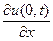
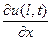
и, кроме того, для функции u(x, t) заданы начальные условия (21), то задачу (15), (19) – (21) называют второй начально-краевой задачей для уравнения теплопроводности. В терминах теории теплообмена граничные условия (19), (20) задают тепловые потоки на концах стрежня для различных моментов времени.
Третья начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия третьего рода, т.е. для x = 0 и x = l заданы линейные комбинации искомой функции и её частной производной по пространственной переменной:
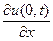
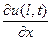
и, для функции u(x, t) заданы начальные условия (21), то задачу (15), (22), (23) называют третьей начально-краевой задачей для уравнения теплопроводности.
В терминах теории теплообмена граничные условия (22), (23) задают теплообмен между газообразной и жидкой средой (которые располагаются с разных «торцов» стержня) и границами расчётной области (т.е. внутренней частью стержня). Из-за теплообмена, температуры u(0, t) и u(l, t) на торцах стержня не известны, а известно, что температуры газообразной и жидкой среды соответственно равны
j 1(t)/a и j 2(t)/b. Параметры a и b являются коэффициентами теплообмена между газообразной или жидкой средой и соответствующей границей стержня.
Дата добавления: 2015-09-14 ; просмотров: 1250 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Постановка краевых задач для уравнения параболического типа
Поставить краевую задачу, соответствующую данной физической задаче – это значит выбрать функцию, характеризующую физический процесс и затем:
а) записать дифференциальное уравнение для этой функции;
б) установить для нее граничные условия;
в) сформулировать начальные условия.
Уравнения и граничные условия краевых задач, например, теории теплопроводности, являются следствием:
1) закона сохранения энергии;
2) закона внутренней теплопроводности в твердых телах (закона Фурье), который в одномерном случае выражается следующим образом:
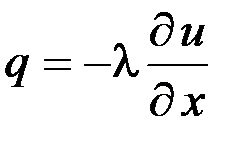
где q – количество тепла, протекающего в единицу времени в направлении оси x через единицу площади;
u – температура в рассматриваемом месте тела;
λ – коэффициент теплопроводности, который зависит от физических свойств тела и от температуры u; но при решении данных задач зависимостью λ от температуры пренебрегаем.
3) закона конвективного теплообмена между поверхностью твердого тела и окружающей его газообразной или жидкой средой (закон Ньютона), который выражается формулой

где q – количество тепла, протекающего в единицу времени через единицу площади поверхности тела в окружающую среду;

u – температура поверхности тела;
θ – температура окружающей среды.
Рассмотрим подробнее, как записываются граничные условия. Они различаются в зависимости от температурного режима на границах рассматриваемой области. Обычно рассматривают три основных типа граничных условий (ограничимся одномерным случаем):
I. Задается температура на поверхности тела. Например, на конце стержня (при x = 0) задана температура

II. Задается поток тепла через поверхности тела (в случае теплоизолированного с боковой поверхности стержня – величина теплового потока, протекающего через торцевое сечение стержня). Например, на концах

где 

Если какой либо конец стержня теплоизолирован, то граничное условие примет вид

III. На поверхности тела происходит теплообмен со средой, имеющей температуру 


где 
Условия (18.7) – (18.9) также можно рассматривать как частный случай общих условий (18.4).
Поток тепла считается положительным, если тепло уходит из стержня в окружающую среду (u > θ), и отрицательным – в противоположном случае.
Согласно закону сохранения энергии количество уходящего тепла должно быть равно потоку тепла, проходящего через рассматриваемое торцевое сечение в силу теплопроводности стержня.
Пусть начало стержня совпадает с началом координат (x = 0), а конец его имеет абсциссу 


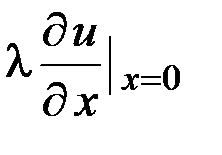







где 
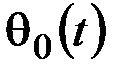
Граничные условия на концах стержня (при x = 0 и 
Кроме описанных выше линейных краевых задач, существуют также задачи с нелинейными граничными условиями, например

Это граничное условие соответствует излучению по закону Стефана – Больцмана в среду с температурой 

Рассмотрим более подробно, например, задачу (с граничными условиями первого рода) для ограниченной области (стержня длиной 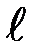


Постановка задач для уравнений параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид

Если на границах х=0 и х=l заданы значения искомой функции u(x,t) в виде

т.е. граничные условия первого рода, и, кроме того, заданы начальные условия
то задачу (2.1)-(2.4) называют первой начально-краевой задачей для уравнения теплопроводности (2.1).
В терминах теории теплообмена u(x,t) – распределение температуры в пространственно-временной области 
Если на границах х=0 и х=l заданы значения производных искомой функции по пространственной переменной


т.е. граничные условия второго рода, то задачу (25.1), (2.5), (2.6), (2.4) называют второй начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки.
Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной


т.е. граничные условия третьего рода, то задачу (2.1), (2.7), (2.8), (2.4) называют третьей начально-краевой задачей для уравнения теплопроводности (2.1). В терминах теории теплообмена граничные условия (2.7), (2.8) задают теплообмен между газообразной или жидкой средой и границами расчетной области с неизвестными температурами u(0,t), u(l,t).
Для пространственных задач теплопроводности в области 
Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения задачи (2.9) – (2.11).
На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.
2.1.2. Понятие о методе конечных разностей. Применение метода конечных разностей к решению уравнений параболического типа
Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начально-краевой задачи для уравнения теплопроводности (2.1)-(2.4). Нанесем на пространственно-временную область 0≤x≤l, 0≤t≤T конечно-разностную сетку ω hτ

с пространственным шагом h=l/N и шагом по времени τ=T/K (рис 2.1).
Введем два временных слоя: нижний t k =kτ , на котором распределение искомой функции u(xj,t k ), известно (при k=0 распределение определяется начальным условием (2.4) u(xj,t 0 )=ψ(xj)) и верхний временной слой t k+1 =(k+1)τ, на котором распределение искомой функции u(xjj,t k+1 ), j=0,1,…,N подлежит определению.
Рис. 2.1. Конечно-разностная сетка
Сеточной функцией задачи (2.1)-(2.4) (обозначение ) назовем однозначное отображение целых аргументов j, k в значения функции
На введенной сетке (2.12) введем сеточные функции 


Подставляя (2.13), (2.14) в задачу (2.1)-(2.4), получим явную конечно-разностную схему для этой задачи в форме

где для каждого j-го уравнения все значения сеточной функции известны, за исключением одного 
Если в (2.14) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое

то после подстановки (2.13), (2.16) в задачу (2.1)-(2.4), получим неявную конечно-разностную схему для этой задачи

Теперь сеточную функцию на верхнем временном слое можно получить из решения СЛАУ (2.17) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке.
Рис. 2.2. Шаблоны явной и неявной конечно-разностных схем для уравнения теплопроводности
На рисунке 2.2 приведены шаблоны для явной (2.15) и неявной (2.17) конечно-разностных схем при аппроксимации задачи (2.1)-(2.4).
Явная конечно-разностная схема (2.15), записанная в форме

обладает тем достоинством, что решение на верхнем временном слое получается сразу (без решения СЛАУ) по значениям сеточных функций на нижнем временном слое 

С другой стороны, неявная конечно-разностная схема (2.17), записанная форме

приводит к необходимости решать СЛАУ, но зато эта схема абсолютно устойчива.
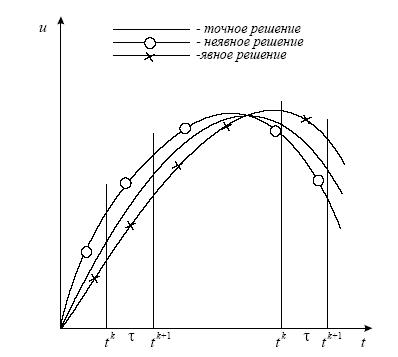
Проанализируем схемы (2.18), (2.19). Пусть точное решение, которое не известно, возрастает по времени, т.е. 

Для неявной схемы (2.19) на возрастающем решении, наоборот, решение завышено по сравнению с точным, поскольку оно определяется по значениям сеточной функции на верхнем временном слое.
На убывающем решении картина изменяется противоположным образом: явная конечно-разностная схема завышает решения, а неявная — занижает (см. рис. 2.3)
Рис. 2.3. Двусторонний метод аппроксимации
На основе этого анализа возникла идея о построении более точной неявно-явной конечно-разностной схемы с весами при пространственных конечно-разностных операторах, причем при измельчении шагов τ и h точное (неизвестное) решение может быть взято в ″вилку″ сколь угодно узкую, т.к. если явная и неявная схемы аппроксимируют дифференциальную задачу и эти схемы устойчивы, то при стремлении сеточных характеристик и h к нулю, решения по явной и неявной схемам стремятся к точному решению с разных сторон.
Рассмотрим неявно-явную схему с весами для простейшего уравнения теплопроводности

где θ — вес неявной части конечно-разностной схемы, 1−θ — вес для явной части, причем 0≤θ≤1. При θ=1 имеем полностью неявную схему, при θ=0 — полностью явную схему, и при θ=1/2 — схему Кранка-Николсона. Для схемы Кранка-Николсона (θ=1/2) порядок аппроксимации составляет , 
Неявно-явная схема с весами (2.20) абсолютно устойчива при 1/2≤θ≤1 и условно устойчива с условием при 0≤θ 0 имеет вид:
Данное уравнение описывает, в частности, процесс малых поперечных колебаний струны. В этом случае u(x,t) — поперечные перемещения (колебания) струны, а – скорость распространения малых возмущений в материале, из которого изготовлена струна.
Если концы струны движутся по заданным законам, то есть на концах заданы перемещения (или значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:

причем, если концы струны жестко закреплены, то ϕ0(t)=ϕl(t)=0.
Как видно, в задачах для волнового уравнения, кроме начального распределения искомой функции, задается еще распределение начальной скорости перемещения.
Если на концах струны заданы значения силы, которая по закону Гука пропорциональна значениям производной перемещения по пространственной переменной (то есть на концах заданы значения первых производных по переменной x), то ставится вторая начально-краевая задача для волнового уравнения:
В условиях, когда концы струны свободны, функции ϕ0(t)=ϕl(t)=0.
Наконец в условиях, когда концы закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, ставится третья начально-краевая задача для волнового уравнения:
Аналогично ставятся двумерные и трехмерные начально-краевые задачи для двумерного и трехмерного волнового уравнения.
3.2 Конечно-разностная аппроксимация уравнений гиперболического типа
Рассмотрим первую начально-краевую задачу для волнового уравнения (3.1)-(3.5). На пространственно-временной сетке (3.12) будем аппроксимировать дифференциальное уравнение (3.1) одной из следующих конечно-разностных схем:


Рис. 3.1. Шаблоны конечно-разностных схем для волнового уравнения
с шаблоном на рисунке 3.1 б
При этом схема (3.6) является явной. С ее помощью решение 

Схема (3.7) является неявной схемой и обладает абсолютной устойчивостью. Ее можно свести к СЛАУ с трехдиагональной матрицей, решаемой методом прогонки.
В обеих схемах необходимо знать значения 

где 
Для определения 
Откуда для искомых значений 
Недостатком такого подхода является первый порядок аппроксимации второго начального условия. Для повышения порядка аппроксимации воспользуемся следующей процедурой.
Разложим 

Для определения второй производной в выражении (3.9) воспользуемся исходным дифференциальным уравнением .
В результате получаем искомую сеточную функцию 

Выписать явную конечно-разностную схему для третьей начально-краевой задачи.
Аппроксимация дифференциального уравнения на шаблоне (3.1б) выглядит следующим образом:
где .
Граничные условия аппроксимируем с первым порядком:


Для окончательного замыкания вычислительного процесса определим, исходя из начальных условий, значения искомой функции на двух первых временных слоях
В начальный момент времени значения 





Тема 4. Разностные схемы для уравнений эллиптического типа Задача Дирихле для уравнения Пуассона в квадрате. Аппроксимация. Однозначная разрешимость. Принцип максимума. Устойчивость. Разностная задача Дирихле в прямоугольнике. Сложная область. Связные и несвязные области. Метод установления. Явная и неявная схемы. Схема переменных направлений. Анализ явной схемы установления и анализ схемы переменных направлений.
Классическим примером уравнения эллиптического типа является уравнение Пуассона
или уравнение Лапласа при f(x,y)≡0.
Здесь функция u(x,y) имеет различный физический смысл, а именно: стационарное, независящее от времени, распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряженностей электрического и магнитного полей, потенциала в силовом поле тяготения и т.п.
Если на границе Г расчетной области 

Если на границе Г задается нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона

При этом n – направление внешней к границе Г нормали.
Более приемлемой является координатная форма краевого условия (4.4)


Наконец третья краевая задача для уравнения Пуассона (Лапласа) имеет вид
4.1. Конечно-разностная аппроксимация задач для уравнений эллиптического типа
Рис. 4.1. Центрально-симметричный шаблон
Рассмотрим краевую задачу для уравнений Лапласа или Пуассона (4.1), (4.2) в прямоугольнике 

На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах с помощью отношения конечных разностей по следующей схеме (вводится сеточная функция 

которая на шаблоне имеет второй порядок по переменным и , поскольку шаблон центрально симметричен.
СЛАУ имеет пяти-диагональный вид (каждое уравнение содержит пять неизвестных и при соответствующей нумерации переменных матрица имеет ленточную структуру). Решать ее можно различными методами линейной алгебры, например, итерационными методами, методом матричной прогонки и т.п.
Рис.4.2 Центрально- симметричный шаблон
Рассмотрим разностно-итерационный метод Либмана численного решения задачи Дирихле (4.1), (4.2). Для простоты изложения этого метода примем , тогда из схемы (4.6 ) получим (k-номер итерации)

На каждой координатной линии (например, 



Рис. 4.3. К разностно-итерационному методу Либмана
Это распределение снова подставляются в (4.8), получаем распределение 

где — 
При решении задач с граничными условиями 2-го и 3-го родов наряду с аппроксимацией дифференциального уравнения производится также аппроксимация граничных условий. Здесь в качестве примера приведем разностную схему, аппроксимирующую третью краевую задачу для уравнения Пуассона в прямоугольнике.
Как и ранее в прямоугольнике 
На этой сетке аппроксимируем дифференциальную задачу во внутренних узлах по рассмотренной выше центрально-разностной схеме




Замечание. Метод простых итераций для решения СЛАУ, возникающих при аппроксимации уравнения Пуассона (Лапласа), отличается довольно медленной сходимостью. Этот недостаток может стать существенным при использовании мелких сеток, когда число уравнений в системе становится большим.
Тема 5. Вариационные и вариационно-разностные методы Метод Ритца. Описание метода Ритца. Формулировка метода и применение для решения разностной задачи Дирихле. Построение простейших разностных уравнений диффузии с помощью метода Ритца.
Глава 4, §4.1, §4.2, §4.3, §4.4 В.С. Владимиров, В.В. Жаринов Уравнения математической физики, М.: Физматлит, 2003.
Тема 6. Численные методы решения интегральных уравнений Метод конечных сумм для решения интегральных уравнений Фредгольма и Вольтерра. Метод вырожденных ядер. Резольвента. Нахождение собственных значений и собственных функций. Метод наименьших квадратов. Методы Монте-Карло.
Соболь И.М.. Численные методы Монте-Карло. М.: Наука, 1973.
Соболь И.М.. Метод Монте-Карло. М.: Наука, 1985.
Список литературы
1 .Калиткин Н.Н. Численные методы. М.: Наука, 1978.
2. Демидович Б.П., Марон И.А., Шувалова Э.Э. Численные методы анализа. М.: Наука, 1967.
3. Бахвалов Н.С. Численные методы. Том 1, изд. 2-е, стереотипное, М.,1975.
4. Ермаков СМ., Михайлов Г.А. Статистическое моделирование. Изд. 2-е. М.: Наука, 1982.
5. Соболь И.М.. Численные методы Монте-Карло. М.: Наука, 1973.
6. Соболь И.М.. Метод Монте-Карло. М.: Наука, 1985.
7. Самарский А.А. Теория разностных схем. М.: Наука, 1977.
8. Марчук Г. И. Методы вычислительной математики. М.:Наука, 1989.
9. Бабенко К.И. Основы численного анализа. М.: Наука. 1986.
10. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т. 1. М.: Наука, 1976, Т. 2. М.: Наука, 1977.
11.Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
12.Годунов С.К., Рябенький B.C. Разностные схемы, введение в теорию. М: Наука, 1977.
13. Васильев Ф.П. Численные методы решения экстремальных задач. – М., 1980 – 520 с. с илл.
14. Габассов Р. Кириллова Ф.М. Принцип максимума в теории оптимального управления. – Минск: Наука и техника, 1974.
15. Гамкрелидзе Р.В. Основы оптимального управления. – Тбилиси: Изд-во Тбилисского ун-та, 1977
1.Шакенов К.К. Методы Монте-Карло и их приложения. Алматы: КазГУ,1993.
2. Дробышевич В.И., Дымников В.П., Ривин Г.С. Задачи по вычислительной математике. М.: Наука, 1980.
3.Копченова Н.В., Марон И.А., Вычислительная математика в примерах и задачах. М.: Наука, 1972.
4.Черкасова М.П. Сборник задач по численным методам. Минск: Высшая школа, 1967.
5.ВазовВ., Дж.Форсайт. Разностные методы решения дифференциальных
уравнений в частных производных. М.: ИЛ, 1963.
6.Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных
систем уравнений со многими неизвестными. М.: Наука, 1975.
7.Митчел Э., Уэйт Р. Метод конечных элементов для уравнений с частными производными. М.: Мир, 1981.
8.Трауб Дж. Итерационные методы решения уравнений. М.: Мир, 1983.
9.Михлин С.Г. Некоторые вопросы теории погрешностей. Л.: ЛГУ, 1988.
10.Михлин С.Г. Вариационные методы в математической физике. М., 1970.
http://lektsii.org/14-37209.html
http://megaobuchalka.ru/1/3242.html