Постановка задачи решения нелинейных уравнений основные этапы

Постановка задачи приближенного решения нелинейных уравнений (НЛУ). Этапы приближенного решения НЛУ

Одной из наиболее распространенных задач математического анализа является задача определения корней нелинейных уравнений (НЛУ) с одним неизвестным. Решение этой задачи имеет целый ряд важных практических приложений.

В общем виде нелинейное уравнение с одним неизвестным можно представить в виде (слайд 2):

f ( x ) = 0

где f(x) – нелинейная функция одной действительной переменной.

В зависимости от вида функции f ( x ) различают алгебраические и трансцендентные уравнения. Алгебраическими уравненияминазываются уравнения, в которых функция f ( x ) представляет собой полином n-й степени (n > 1):

Всякое неалгебраическое уравнение называется трансцендентным уравнением. Функция f(x) в таких уравнениях представляет собой выражение, содержащее хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую, обратную тригонометрическую или их комбинацию.

Решить НЛУ – означает найти его корни (слайд 3). Число x * называется корнем уравнения f ( x ) = 0, если при подстановке его в функцию f ( x ) она обращается в 0, а уравнение – в тождество.

Однако точные значения корней могут быть найдены аналитически только для некоторых типов уравнений. В частности, формулы, выражающие решение алгебраического уравнения, могут быть получены лишь для уравнений не выше четвертой степени. Еще меньше возможностей для получения точного решения трансцендентных уравнений. В этих случаях ставится задача приближенного решения НЛУ:

найти приближенное решение НЛУ с погрешностью, не превышающей ε > 0, то есть удовлетворяющее неравенству

В существующих методах приближенного решения НЛУ предполагается, что известен отрезок [a;b], на котором находится один и только один корень уравнения. Для отыскания всех корней уравнения должно быть задано несколько таких отрезков, и отыскание каждого корня проводится независимо друг от друга. Поэтому приближенное решение НЛУ распадается на 2 этапа (слайд 4):

1) отделение корней, то есть определение достаточно малых отрезков, в каждом из которых содержится один и только один корень уравнения;

2) уточнение корней на каждом из полученных отрезков с наперед заданной точностью.

Уточнение корней производится итерационными методами, то есть путем построения последовательности приближений к корню x * : x ₀ , x ₁ , . x_n, … Если такая последовательностьпри n ® ¥ имеет предел, равный точному значению корня x * , то говорят, что итерационный процесс сходится. В качестве приближенного решения уравнения выбирается первое последовательное приближение x_k, попавшее в ε–окрестность корня x * .

Различные численные методы уточнения корня могут обладать разной скоростью сходимости и трудоемкостью вычисления очередного приближения. Чем меньшее количество итераций требуется для достижения одной и той же точности при одном и том же начальном приближении, тем более высокой скоростью сходимости обладает тот или иной метод.

Численное решение нелинейного уравнения. Этапы решения.

f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.

Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.

Задача нахождения корней состоит из 2 этапов:

1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.

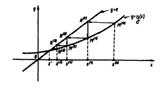
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:

[a;b] – интервал изоляции корня. Для каждого корня уравнения определяется интервал его изоляции [a;b]. На отрезке [a;b] должен находиться 1 корень.

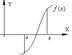
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.

Классификация методов уточнения корней :

1) Метод половинного деления отрезка(дихотомии).

Отрезок [a;b], содержащий единственный корень, делят пополам, отбрасывают ту половину, где нет корня. Процесс повторяется до тех пор, пока длина отрезка не станет меньше заданной погр. E.

Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.

Построение последовательных хорд, в качестве приближений к корню принимаются значения их пересечения с осью абсцисс.

Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).

3) Метод касательных( метод Ньютона)

В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.

Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).

4) Комбинированный метод – объединение методов хорд и касательных.

Приближение к корню на каждой итерации происходит одновременно с 2 сторон интервала [a;b]. Одной стороны строится хорда, а с другой касательная.

Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).

5) Метод простой итерации.

Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.

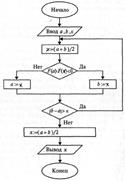
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм. Требуется вычислить корень уравнения f(x)=0 на [a;b] с заданной погрешностью Е. Отрезок [a;b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е. Алгоритм метода:

46)Уточнение корня нелинейного уравнения методом хорд. Схема алгоритма.Требуется вычислить корень уравнения f(x)=0 на [a,b] с заданной погрешностью е. Геометр-ки метод основан на построении последовательности хорд. Ур-е хорды . В данном методе процесс итерации состоит в том, что в качестве приближений к корню уравнение f(x)=0 принимаются значения х₁, х₂… х_i точек пересечения хорды АВ с осью абсцисс. Если f(a)>0 , то левая граница a неподвижна, х₀=b и из урав. хорды получим: Если f(a) 0 и f’’(x)>0 при a≤x≤b. Тогда для приближения к корню со стороны границы а используем построение хорды, а со стороны границы b – касательная. На 1й итерации строим хорду А₀В₀ и проводим касательную в точку В₀. Левую границу а переносим в а₁, правую – b_1. На каждой итерации для вычисления новых границ интервала используют ф-лы хорд и касательных : , . Сужение интервала проводим до тех пор пока он не станет

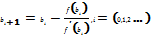
Постановка задачи. Основные этапы решения

Решение нелинейных уравнений

Методы решения нелинейных уравнений – редкий пример задачи, которая ([3], стр. 85): может быть сравнительно полно исследована элементарными средствами; допускает наглядное геометрическое истолкование; проблемы, возникающие при отыскании корней нелинейных уравнений – типичны; некоторые методы их решения (например – простой итерации и метод Ньютона) допускают широкие обобщения и играют в вычислительной математике фундаментальную роль.

Постановка задачи. Основные этапы решения

Пусть задано уравнение:

. (4.1)

Корнем уравнения (или решением) уравнения (4.1) называется значение , при котором .

Корень уравнения (4.1) называется простым, если , в противном случае, т.е. когда, , корень уравнения (4.1) называется кратным. Натуральное число m называется кратностью корня , если ([3], стр. 85). Иногда простой корень называют корнем кратности 1.

С геометрической точки зрения, корень уравнения (4.1) соответствует точке пересечения графика функции с осью ОХ. Причем, если корень — простой, то график функции пересекает ось абсцисс под ненулевым углом, а если — кратный корень, то – под нулевым углом.

Наиболее часто встречающимися и соответственно разработанными (на данном этапе) являются методы отыскания простых корней.

Как правило, в конкретной задаче, интерес представляют не все корни уравнения, а лишь некоторые из них, поэтому задачу обычно уточняют дополнительными ограничениями (положительные, отрицательные, наименьший, наибольший, на определенном промежутке и т.д.).

К сожалению, в подавляющем случае представить решение уравнения (4.1) в виде конечной формулы не представляется возможным. Но в ходе вычислительного эксперимента, это не должно вызывать особых огорчений.

1) В реальных исследованиях зависимость является лишь приближенным описанием, моделирующим связь между х и у. Следовательно, даже точное решение уравнения (4.1) является лишь приближением того параметра х, который в действительно соответствует значению у = 0.

2) Даже если уравнение (4.1) допускает возможность нахождения в виде конечной формулы, то результат вычислений по этой формуле (за очень редким исключением) содержит вычислительную погрешность и, следовательно, является приближенным.

Решение задачи отыскания корней нелинейного уравнения (4.1) осуществляют в два этапа ([3], стр. 87):

1 этап – локализация (отделение) корней;

2 этап – итерационное уточнение корней.

Рассмотрим более подробно каждый из данных этапов.

Отрезком локализации корня уравнения (4.1) называется отрезок [a, b], содержащий только один корень данного уравнения ([3], стр. 88).

Цель данного этапа считается достигнутой, если для каждого из подлежащих определению корней (согласно постановке исходной задачи) удалось указать отрезок локализации (его длину стараются сделать возможно минимальным).

Как правило, сначала стараются определить существуют ли корни у уравнения (4.1), сколько их, как они расположены, а затем приступают к определению (выбору, уточнению) отрезков локализации.

Наиболее простыми способами выяснения вопроса о существовании корней являются: графический и табличный.

Графический способ: исходное уравнение (4.1) представляют в эквивалентном виде (4.2):

, (4.2)

затем строят графики функций и , находят точки пересечения этих графиков. Абсциссы точек пересечения – корни соответствующего уравнения.

Табличный способ:строят таблицы значений функциивида , и выделяют отрезки , ; для которых (т.е. функция на концах отрезков принимает значения разных знаков), так как согласно теореме 4.1 внутри этого отрезка обязательно найдется корень уравнения (4.1).

Теорема 4.1 ([7], стр. 247) Если функция непрерывна на отрезке [a, b] и принимает на концах отрезка значения разных знаков, т.е. , то найдется точка , такая что .

Однако табличный метод имеет существенные недостатки:

1) если шаг (расстояние между и ), с которым вычисляются значения будет достаточно большим, можно пропустить отрезки, содержащие корни уравнения (следовательно, необходимо составлять несколько таблиц);

2) даже с помощью очень подробной таблицы не удастся выявить корни четной кратности, так как в окрестности таких корней функция имеет постоянный знак ([3], стр. 88);

3) он не обеспечивает локализацию (единственность) корней.

Для проверки правильности результатов, получаемых с помощью графического и табличного методов, и окончательного решения вопроса об отрезке локализации корня применяется аналитический метод, в основе которого лежит теорема 4.2, являющаяся следствием к теореме 4.1.

Теорема 4.2 ([6], стр. 16) Если функция непрерывна на [a, b] и дифференцируема на (a, b), принимает на концах отрезка значения разных знаков ( ), или , то найдется единственная точка , такая что .

Если на отрезке, выбранном с помощью графического или табличного способа, условия теоремы не выполняются (чаще всего это касается соответствующих свойств производной), то его разбивают на новые отрезки, до тех пор, пока не удастся выделить отрезки, содержащие только один корень уравнения.

Если аналитический метод применяется независимо от табличного и графического, то для определения отрезков локализации корней уравнения (4.1) область определения функции разбивают точками (случае необходимости повторяя этот процесс несколько раз, увеличивая число промежутков) до тех пор, пока не станут выполняться условия (4.3):

(4.3)

После выбора отрезка локализации наступает этап уточнения корней. Его осуществляют различными итерационными методами, в основе каждого из которых лежит построение последовательности …, (или … ) приближений к точному корню уравнения (4.1), т.е. построение последовательности , такой, что . Каждый член соответствующей последовательности будет давать приближенное значение корня с абсолютной погрешностью .

Критерием окончания итерационного процесса является достижение заданной точности e, т.е. выполнение условия . Значение в этом случае считается приближенным значением корня с точностью .

В настоящее время известно достаточно много различных алгоритмов построения соответствующих последовательностей приближений, среди которых выделяются ([3], стр. 90):

· одношаговые – когда для построения очередного приближения используется только одно предыдущее значение ,

· к – шаговые – когда для построения приближения используются к предшествующих значений .

Нетрудно заметить, что для построения итерационной последовательности одношаговым методом требуется задание одного начального приближения, для к-шаговых методов – к начальных приближений .

Сходимость последовательности к называется линейной (соответственно, итерационный процесс – линейно сходящимся), если найдутся постоянная и номер , такой что , и сверхлинейной, если существует такая положительная последовательность , что и ([5], стр. 201).

Последовательность сходится к по меньшей мере с р-м порядком (соответственно, итерационный процесс имеет по меньшей мере р-й порядок) если найдутся постоянные и , и номер , такой что ([5], стр. 201).

К линейной сходимости применяют также термин «сходимость со скоростью геометрической прогрессии» ([5], стр. 201). В [3], стр. 90 дается более строгое определение сходимости со скоростью геометрической прогрессии:

метод сходится со скоростью геометрической прогрессии, знаменатель которой , если для всех n справедлива оценка .

Мы будем рассматривать следующие методы: бисекций (общий алгоритм, метод деления отрезка пополам и метод хорд), метод Ньютона и метод простых итераций. Данные методы отличаются как алгоритмами задания формул для построения последовательности приближений, так и скоростью сходимости (числом итераций, необходимых для достижения требуемой точности), так и типом сходимости.

Прежде, чем мы перейдем к описанию алгоритмов построения итерационных последовательностей для каждого из указанных методов, проанализируем меру обусловленности задачи отыскания корня уравнения (4.1).

Если функция f (x) в уравнении (4.1) является непрерывной, то для точек из окрестности корня выполняется следующее свойство:

. (4.4)

Интервал называется интервалом неопределенности, а — радиус интервала неопределенности ([3], стр. 93).

Если — простой корень, то используя разложение по формуле Тейлора второго порядка (с остаточным членом в форме Пеано или Лагранжа), можно получить, что

,

,

,

,

откуда следует, что интервал неопределенности и радиус неопределенности определяются по формулам (4.5):

, ; (4.5)

абсолютное число обусловленности задачи отыскания простого корня уравнения (4.1) равно:

. (4.6)

Из формул (4.3) следует, что радиус интервала неопределенности пропорционален погрешности вычисления значения f и погрешность возрастает с уменьшением , т.е. с уменьшением модуля угла, при котором график функции пересекает ось абсцисс.

Если — корень кратности m, то, применяя формулу Тейлора уже порядка , получаем:

,

,

,

,

откуда следует, что интервал неопределенности и радиус неопределенности определяются по формулам (4.7):

, . (4.7)

Из формулы (4.7) следует, радиус интервала неопределенности кратен , что соответствует плохой обусловленности задачи поиска кратного корня.

Исследователи ([3], стр. 94) отмечают, что в реальных расчетах оценить значение и порядок радиуса интервала неопределенности достаточно сложно. Однако знать о его существовании необходимо, так как:

1) не имеет смысла ставить задачу о поиске решения с точностью ;

2) любое число из интервала неопределенности с одной и той же степенью достоверности можно принимать за приближенное решение уравнения (4.1);

3) нельзя требовать от алгоритмов отыскания корня получения достоверных результатов после того, как очередное приближение попало в интервал неопределенности или оказалось достаточно близко от него, поэтому рекомендуется расчеты прекращать и считать, что результат соответствует максимально возможному.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.017 сек.)