Построение уравнения непосредственно на основе исходных данных

Учебные материалы для студентов

Методические указания, конспекты, лекции, контрольные, лабораторные работы, курсовые.

Тест по эконометрике

Тест №1

Первая главная компонента

A. Содержит максимальную долю изменчивости всей матрицы факторов.
B. Отражает степень влияния первого фактора на результат.

C. Отражает степень влияния результата на первый фактор.

D. Отражает долю изменчивости результата, обусловленную первым фактором.

E. Отражает тесноту связи между результатом и первым фактором.

Если расчетное значение F-критерия Фишера превышает табличное, то можно сделать вывод о.

статистической незначимости построеной модели

значимости(существенности) моделируемой зависимости

статистической значимости построенной модели

невозможности использования построенной модели для описания исследуемой зависимости

При применении метода наименьших квадратов к оценке параметров уравнений регрессии, величина зависимой переменной у не может определяться на основании ____________ уравнения регрессии

Выберите по крайней мере один ответ: дифференциального

линеаризованного

нелинейного

Фиктивной переменными в уравнении множественной регрессии могут быть.

a. количественные переменные

b. экономические показатели, выраженные в стоимостном измерении

c. качественные переменные, преобразованные в количественные

d. переменные, исходные значения которых не имеют количественного значения

Косвенный метод наименьших квадратов применим для .

a. идентифицируемой системы одновременных уравнений

b. неидентифицируемой системы рекурсивных уравнений

c. неидентифицируемой системы уравнений

d. любой системы одновременных уравнений

Индекс корреляции рассчитанный для нелинейного уравнения регрессии характеризует .

тесноту нелинейной связи между зависимой и независимой переменными

на сколько процентов изменится значение зависимой переменной при изменении на один процент независимой переменной

статистическую значимость (существенность) связи построенного уравнения

значение арифметического корня, взятого по значению индекса детерминации для этого нелинейного уравнения

Двухшаговый метод наименьших квадратов применим для .

Выберите один ответ.

сверхидентифицируемой системы одновременных уравнений

идентифицируемой системы одновременных уравнений

любой системы одновременных уравнений

неидентифицируемой системы уравнений

В роли расстояния между объектами может выступать

Выберите по крайней мере один ответ: обычное евклидово расстояние

квадрат евклидового расстояния

косинус угла между объектами-векторами

максимум модуля разности между координатами

Структурная форма системы эконометрических уравнений это.

Выберите один ответ.

a. система регрессионных уравнений, в каждом из которых содержатся все объясняемые переменные из других уравнений

b. система регрессионных уравнений, матрица коэффициентов которых симметрична

c. система уравнений регрессии, имеющих треугольную структуру

d. исходные уравнения регрессии, каждое из которых в качестве объясняющей переменной может содержать объясняемую переменную из других уравнений

Число главных компонент

Выберите один ответ.

A. Больше числа исходных факторов, но меньше длины базисного ряда данных.

B. Меньше числа исходных факторов.

C. Равно числу исходных факторов.

D. Равно длине базисного ряда данных.

E. Больше длины базисного ряда данных.

Значение коэффициента детерминации, рассчитанное для линейного уравнения парной регрессии составило . Следовательно, значение линейного коэффициента парной корреляции может быть равно

Выберите по крайней мере один ответ: -0.9; если b 0

Целью дискриминантного анализа является

Выберите один ответ. количество верно классифицированных объектов близко к 50%

количество верно классифицированных объектов близко к 100%

все группы имеют одинаковую размерность

При применении метода наименьших квадратов к линейному уравнению регрессии минимизируется сумма квадратов.

Выберите по крайней мере один ответ:

отклонений фактических (наблюдаемых) y от их модельных значений , рассчитанных по уравнению величин

Временным рядом называют.

Выберите один ответ.

a. Временно созданный набор данных

b. Упорядоченные во времени значения показателя

c. Ряд данных, полученный расчетным путем за короткое время

d. Набор данных для исследования

Главные компоненты представляют собой

Выберите один ответ. A. Статистически значимые факторы.

B. Экономически значимые факторы.

C. Линейные комбинации факторов.

D. Центрированные факторы.

E. Пронормированные факторы.

Значение коэффициента детерминации рассчитывается как отношение дисперсии результативного признака, объясненной регрессией, к __________ дисперсии результативного признака

Выберите один ответ.

Укажите уравнения регрессии, в которых фиктивная переменная используется только в мультипликативной форме.

При построении дендрограммы сначала объединяются

Выберите один ответ. объекты, совпадающие по всем признакам

наиболее близкие объекты относительно выбранного расстояния

наиболее далекие объекты

Автокорреляцией уровней временного ряда называют.

Выберите один ответ.

a. корреляционную зависимость между трендовой и сезонной компонентами временного ряда

b. корреляционную зависимость между наблюдаемыми и расчетными значениями исследуемого временного показателя

c. корреляционную зависимость между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на один или несколько периодов времени

d. автокорреляцию остатков временного ряда

С помощью частного F-критерия можно проверить значимость j-го коэффициента чистой регрессии в предложении, что j-й фактор в уравнение множественной регрессии.

Выберите один ответ. a. не был включен

b. был включен последним

c. был включен первым

d. был включен условно

Если оценки параметров уравнения регрессии, полученных при помощи метода наименьших квадратов обладают свойствами несмещенности, эффективности и состоятельности, то .

Выберите по крайней мере один ответ:

a. математическое ожидание остатков равно нулю и они характеризуются минимальной дисперсией

b. происходит накапливание значений остатков при большом числе выборочных оцениваний

c. возможен переход от точечного оценивания к интервальному

d. наблюдается уменьшение точности оценивания параметров с увеличением объема выборки

Компонентами временного ряда являются:

Выберите по крайней мере один ответ:

циклическая (сезонная) компонента

Качество подбора нелинейного уравнения регрессии можно охарактеризовать на основе показателей.

Выберите по крайней мере один ответ:

средней ошибки аппроксимации

коэффициента линейной корреляции

При работе по методу К-средних

Выберите по крайней мере один ответ:

элементы не могут переходить из одного кластера в другой

элементы могут переходить из одного кластера в другой

процесс заканчивается при стабилизации кластеров

процесс заканчивается за одну итерацию

В правой части структурной формы взаимозависимой системы могут стоять

Выберите один ответ.

A. Только экзогенные лаговые переменные.

B. Только экзогенные переменные (как лаговые, так и нелаговые).

C. Только эндогенные лаговые переменные.

D. Только эндогенные переменные (как лаговые, так и нелаговые).

E. Любые экзогенные и эндогенные переменные.

Одним из современных препятствий эффективного применения множественного регрессионного анализа является

Выберите один ответ.

a. малая диcперсия

b. мультиколлинеарность независимых переменных

c. низкая квалификация исследователя

d. малое количество факторов

Гипотеза об мультипликативной структурной схеме взаимодействия факторов, формирующих уровни временного ряда, означает правомерность следующего представления .

Выберите один ответ.

a. уровень тренда равен уровень временного ряда * конъюнктурная компонента * сезонный фактор * случайная компонента

b. уровень временного ряда равен (тренд + конъюнктурная компонента)*сезонный фактор + случайная компонента

c. случайная компонента равна тренд * конъюнктурная компонента * сезонный фактор * уровень временного ряда

d. уровень временного ряда равен тренд * конъюнктурная компонента * сезонный фактор * случайная компонента

Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то .

Выберите по крайней мере один ответ:

при большом числе выборочных оцениваний остатки не будут накапливаться

возможен переход от точечного оценивания к интервальному

точность модели снижается с увеличением объема выборки

предпосылки метода наименьших квадратов не выполняются

На практике для анализа коррелированности отклонений используют статистику.

Выберите один ответ.

Перечислить основные методы кластерного анализа

Выберите по крайней мере один ответ:

Параметр является статистически значимым (существенным), если

Выберите один ответ.

a. он положителен

b. вероятность того, что он равен нулю мала

c. известна формула для его расчета

d. вероятность того, что он не равен нулю мала

Целью кластерного анализа является

Выберите один ответ.

A. образование групп схожих между собой объектов

B. разбиение на группы по некоторым признакам

C. различение объектов наблюдения по некоторым признакам

D. извлечение наиболее важных факторов из групп данных

Показателями качества нелинейного уравнения парной регрессии является.

Выберите по крайней мере один ответ:

коэффициент нелинейной регрессии

множественный коэффициент корреляции

Тест №2

Целью дискриминантного анализа является
все группы имеют одинаковую размерность
количество верно классифицированных объектов близко к 100%
количество верно классифицированных объектов близко к 50%

Установите соответствие между наименованиями уравнений множественной регрессии:
построение уравнения на основе выровненных центрированных данных
построение уравнения регрессии на основе исходных данных для двух независимых переменных и расчетом средних значений для других независимых переменных
построение уравнения непосредственно на основе исходных данных
построение уравнения регрессии на основе исходных данных для одной независимой переменной и расчетом средних значений для других независимых переменных

Структурной формой модели называется система .
a. независимых уравнений
b. уравнений с фиксированным набором факторов
c. взаимосвязанных уравнений
d. рекурсивных уравнений

Число главных компонент
A. Больше числа исходных факторов, но меньше длины базисного ряда данных.
B. Меньше числа исходных факторов.
C. Равно числу исходных факторов.
D. Равно длине базисного ряда данных.
E. Больше длины базисного ряда данных.

Трендовая составляющая временного ряда характеризует.
a. периодические изменения уровней ряда
b. основную тенденцию уровней ряда
c. качество построенной модели временного ряда
d. структуру временного ряда

Если расчетное значение F-критерия Фишера меньше табличного, то можно сделать вывод о.
статистической незначимости построенной модели
статистической значимости построения модели
незначимости(несущественности) моделируемой зависимости
целесообразности использования построенной модели для описания исследуемой зависимости

Главные компоненты представляют собой
A. Статистически значимые факторы.
B. Экономически значимые факторы.
C. Линейные комбинации факторов.
D. Центрированные факторы.
E. Пронормированные факторы.

Целью кластерного анализа является
A. образование групп схожих между собой объектов
B. разбиение на группы по некоторым признакам
C. различение объектов наблюдения по некоторым признакам
D. извлечение наиболее важных факторов из групп данных

Факторы множественной линейной регрессионной зависимости не коррелируют между собой, тогда матрица парных коэффициентов корреляции является.
a. симметричной
b. нулевой
c. единичной
d. треугольной

Если значение коэффициента корреляции, рассчитанное для линейного уравнения регрессии равно единице, то .
связь между параметрами и функциональная
связь между переменными и функциональная
величина оказывает существенное влияние на переменную
величина не оказывает влияния на переменную

С помощью традиционного метода наименьших квадратов можно определить параметры уравнений, входящих в систему _____ уравнений.
a. независимых или рекурсивных
b. одновременных или независимых
c. рекурсивных или одновременных
d. одновременных

Все нижеприведенные нелинейные модели можно свести к модели множественной линейной регрессии . Установите соответствие между видом нелинейной модели и соотношениями между исходными параметрами a, b, c и параметрами линеаризованой модели

В роли расстояния между объектами может выступать
обычное евклидово расстояние
квадрат евклидового расстояния
косинус угла между объектами-векторами
максимум модуля разности между координатами

Аддитивно мультипликативная модель содержит компоненты в виде .
a. отношений
b. слагаемых
c. комбинации слагаемых и сомножителей
d. сомножителей

Перечислить основные методы кластерного анализа
К-средних
дивизимный
агломеративный
главных компонент

Выберите значение коэффицента корреляции, которое характеризует функциональность связи между переменными y и x.

Установите соответствие между видом модели и ее характеристиками.

На практике гетероскедастичность имеет место, когда.
a. вероятностные распределения случайных отклонений при различных наблюдениях будут одинаковы
b. вероятностные распределения случайных отклонений при различных наблюдениях будут различны
c. дисперсия случайных отклонений одинаковы для разных наблюдений
d. дисперсия случайных отклонений является постоянной величиной

Укажите группы факторов, формирующих уровень временного ряда:

временные факторы
случайные факторы
факторы, формирующие тенденцию ряда
факторы, формирующие циклические колебания ряда

Производственная функция Кобба-Дугласа относится к классу ___ моделей.
полулогарифмических
степенных
линейных
обратных

Какое условие не выполняется, если коэффициент регрессии является незначимым(несущественным)?
a. несущественность влияние соотвествующей независимой переменной на зависимую переменную
b. его значение признается равным нулю
c. его значение признается отличным от нуля
d. соответствующая независимая переменная не включается в модель

При построении дендрограммы сначала объединяются
наиболее далекие объекты
объекты, совпадающие по всем признакам
пропорциональные объекты
наиболее близкие объекты относительно выбранного расстояния
Вопрос 26

Первая главная компонента
A. Содержит максимальную долю изменчивости всей матрицы факторов.
B. Отражает степень влияния первого фактора на результат.
C. Отражает степень влияния результата на первый фактор.
D. Отражает долю изменчивости результата, обусловленную первым фактором.
E. Отражает тесноту связи между результатом и первым фактором.

Эконометрическая модель, являющаяся системой одновременных уравнений, состоит в общем случае .
a. из поведенческих уравнений и автокорреляционной функции
b. из поведенческих уравнений и тождеств
c. только из тождеств
d. из регрессионных уравнений и соотношений мультиколлинеарности в каждом из них

Если оценки параметров уравнения регрессии обладают свойствами состоятельности, эффективности и несмещенности, то .
предпосылки метода наименьших квадратов не выполняются
возможен переход от точечного оценивания к интервальному
точность модели снижается с увеличением объема выборки
при большом числе выборочных оцениваний остатки не будут накапливаться

При величине лага, равной нулю, автокорреляционная функция .
a. не существует
b. равна -1
c. равна 0
d. равна 1

Укажите последовательность этапов обобщенного метода наименьших квадратов.
изменяется спецификация модели (путём преобразования уравнения с учётом коэффициента пропорциональности дисперсий остатков)
устанавливается наличие гетероскедаcтичности или автокорреляции остатков
оцениваются параметры новой модели
оценивается общее качество преобразованной модели

Нарушение предпосылок метода наименьших квадратов ведет к нарушению свойств _________ оценок параметров уравнения регрессии.
a. несостоятельности
b. оперативности
c. эффективности
d. несмещенности

При работе по методу К-средних
элементы не могут переходить из одного кластера в другой
элементы могут переходить из одного кластера в другой
процесс заканчивается при стабилизации кластеров
процесс заканчивается за одну итерацию

Косвенный метод наименьших квадратов применим для .
a. неидентифицируемой системы рекурсивных уравнений
b. идентифицируемой системы одновременных уравнений
c. неидентифицируемой системы уравнений
d. любой системы одновременных уравнений

также в рубрике Контрольные, тесты:

Построение уравнения непосредственно на основе исходных данных

Технологии прогнозирования деятельности предприятия с помощью Microsoft Excel .

Технологии прогнозирования основываются на двух важнейших методах составления прогноза:

· Анализ временных рядов;

· Корреляция и регрессионный анализ

В основе АНАЛИЗА ВРЕМЕННЫХ РЯДОВ – допущение о наличии информации за ряд прошлых периодов. Эти данные позволяют выявить долгосрочные тенденции и повторяющиеся циклы.

При отсутствии данных за прошлые периоды прибегают к КОРРЕЛЯЦИИ: рассматривают показатели с целью выявления возможной взаимосвязи между ними. И далее применяют технику проведения РЕГРЕССИОННОГО АНАЛИЗА для построения уравнения, описывающего выявленную взаимосвязь.

Прогнозирование на основе зависимости между двумя переменными (корреляция и регрессия).

В регрессионном анализе изучается односторонняя зависимость переменной Y от одной или нескольких переменных Х ₁ …., Х _k . Основная задача регрессионного анализа – установление формы зависимости между зависимой ( Y ) и независимыми (Х ₁ …., Х _k ) переменными и анализ достоверности параметров этой зависимости. Такие переменные, как расходы на рекламу, транспорт, численность населения и т.п. являются независимыми переменными, а те переменные, которые мы пытаемся оценить (например, объем продаж), являются зависимыми переменными.

Схема составления прогноза заключается в сборе данных о значениях зависимых и независимых переменных, их анализе на предмет наличия связи (корреляция) и выведении математического уравнения, описывающего эту связь (регрессия).

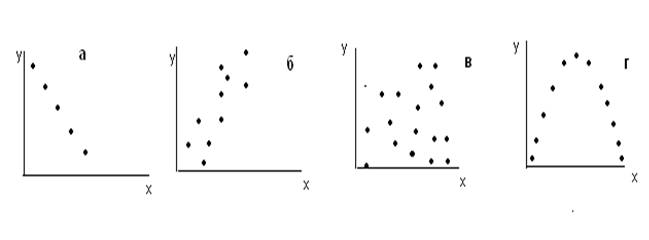
Первая стадия корреляционного анализа – сбор данных о значениях переменных и составления точечных диаграмм (Х Y -диаграммы). Точечные диаграммы имеют различный вид:

Так, на рис. а пример абсолютной отрицательной корреляции, на рис.б – сильной положительной корреляции. На рис. в – взаимосвязь между значениями не усматривается, на рис. г взаимосвязь наличествует, но это не линейная зависимость, а параболическая.

Предположение наличия линейной зависимости между двумя переменными основывается на значении коэффициента корреляции r , который рассчитывается по формуле:

, (1.1)

где n – число пар значений переменных, а Σ символ суммирования.

Значение коэффициента корреляции колеблется от -1 ( в случае абсолютной отрицательной корреляции) до +1 (в случае абсолютной положительной корреляции). Такие диаграммы как показаны на рис. в, г , дадут коэффициенты корреляции почти равные нулю. Хотя на рис. г точки взаимосвязаны между собой, но там зависимость параболическая, а коэффициент корреляции измеряет тесноту линейной связи. Это свидетельствует о важности не только расчетов, но и рассмотрения точечной диаграммы, поскольку даже при r близким к нулю возможно тесная взаимосвязь, но не линейная, а, например, параболическая как показано на рис. г.

Если установлена тесная линейная корреляция между переменными, то можно вывести уравнение прямой и использовать её для прогнозирования поведения зависимой переменной в будущем. Этот процесс носит название ЛИНЕЙНОЙ РЕГРЕССИИ.

Уравнение прямой (линейной) регрессии имеет общий вид:

где y – результативный показатель; х – независимая переменная (фактор); a и b представляют собой константы, их значения определяют положение и направленность прямой в осях координат.

Константа а называется точкой пересечения прямой с осью ординат и её значение представляет собой значение у, когда х=0. Константу b называют коэффициентом при х.

Задача регрессионного анализа заключается в экспериментальном определении коэффициентов регрессии, путем наблюдения за характером изменения входных параметров (факторов) и выходной величины (результативного показателя). Линейная модель уравнения регрессии строится по методу наименьших квадратов. Этот критерий минимизирует сумму квадратов вертикальных отклонений точек от прямой регрессии.

В реальных процессах зависимость результативного показателя у зависит от целого ряда переменных (факторов) х ₁ , х₂, …, х _k . – и это будет множественная регрессия. Модель множественной регрессии имеет следующий вид:

(1.2)

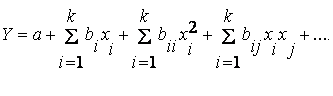
где b_i – линейные коэффициенты_, b_ii – нелинейные коэффициенты, b_ij — коэффициенты, учитывающие взаимное влияние факторов.

Для анализа общего качества регрессии используют коэффициент детерминации (определенности) R 2 . Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. Т.е. с увеличением объясняемой доли разброса R 2 à 1.

Значимость уравнения регрессии определяют, используя критерий Фишера ( F -критерий). Расчетное значение F _в сравнивается с критическим значением ( F _кр ), определяемого по таблице критических точек распределения Фишера: F _кр = k / n – k – 1 ; где k — число факторов, ( n — k -1) – число степеней свободы знаменателя и n – это число параллельных опытов. Если F _в > F _кр — то полученное уравнение регрессии значимо, т.е. хотя бы один из коэффициентов уравнения не равен нулю.

Значимость коэффициентов регрессии проверяется с помощью t -критерия, основанного на распределении Стьюдента. Если вычисленный t -критерий коэффициента b_i ( ç t_bi ê ) больше t _кр ., то коэффициент значимый и влияние соответствующего фактора значимо . t _кр определяют по уровню значимости и числу степеней свободы f = n — k -1.

В табличном процессоре MS Excel значения статистических функций удобно вычислять при помощи мастера функций. Для выполнения статистического анализа имеется набор средств анализа данных, называемый Пакет анализа. Для работы с дополнением Пакет анализа следует задать Сервис-Анализ данных. При отсутствии в меню этой команды следует задать Сервис — Надстройки и в появившемся диалоговом окне Надстройки включить переключатель Пакет анализа, нажать кнопку ОК. Начнет загружаться пакет Анализ данных.

В пакете Анализ данных инструмент Регрессия предлагает линейный регрессионный анализ, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Для вычисления коэффициентов регрессии, определяющих нелинейную зависимость и взаимное влияние факторов необходимо факторы переобозначить . Например, выходной параметр Y зависит от трех факторов: y = f ( x ₁ , x ₂ , x ₃ ).

Записываем значения этих факторов, квадраты факторов, их взаимные произведения и переобозначаем их: x ₁ ® x ₁ , x ₂ ® x ₂ , x ₃ ® x ₃ , 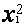® x ₄ , x ® x , x ® x , x ® x , x ® x , x ® x , x ® x . В результате можно построить линейную модель с использованием уравнения (1.2) вида:

Проведя обратные переобозначения , получим модель, учитывающую нелинейность и взаимное влияние факторов:

Лабораторная работа 1.1.

Составление прогноза с использованием линейного уравнения регрессии. Расчет коэффициента корреляции.

Отдел маркетинга компании по продаже модной одежды «Пандора» намеревается изучить наличие взаимосвязи между объемом продаж в каждом отделении сети магазинов фасонной одежды и численностью населения, проживающего в радиусе 30-минутной езды от каждого из отделений.

Отдел располагает данными среднего еженедельного оборота в десяти отделениях сети магазинов компании и сведениями о численности населения:

ВЫЧИСЛИТЕЛЬНАЯ МОДЕЛЬ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ПРИБЛИЖЕННЫМИ ИСХОДНЫМИ ДАННЫМИ НА ОСНОВЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ВОЛЬТЕРРЫ ВТОРОГО РОДА Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Наац В.И., Ярцева Е.П., Андрухив Л.В.

В математических моделях физических явлений, использующих результаты экспериментов, зачастую возникает необходимость решения дифференциальных уравнений. Подобные задачи относятся к классу некорректных математических задач. В данной работе для получения приближенного решения дифференциального уравнения первого порядка с определенными краевыми условиями выполняется построение соответствующего регуляризирующего алгоритма. Реализуется метод, заключающийся в построении эквивалентного исходному дифференциальному уравнению интегрального уравнения Вольтерры второго рода . Для его численного решения приводится вычислительный алгоритм , позволяющий получать устойчивые решения некорректной задачи.

Похожие темы научных работ по математике , автор научной работы — Наац В.И., Ярцева Е.П., Андрухив Л.В.

COMPUTATIONAL MODEL FOR A DIFFERENTIAL EQUATION WITH APPROXIMATE INITIAL DATA BASED ON THE VOLTERRA INTEGRAL EQUATION OF THE SECOND KIND

In mathematical models of physical phenomena that use the results of experiments, it is often necessary to solve differential equations. Such problems belong to the class of incorrect mathematical problems. In this paper, to obtain an approximate solution of a firstorder differential equation with certain boundary conditions, the corresponding regularizing algorithm is constructed. A method is implemented that consists in constructing a Volterra integral equation of the second kind equivalent to the original differential equation. For its numerical solution, we present a computational algorithm that allows us to obtain stable solutions to an illposed problem.

Текст научной работы на тему «ВЫЧИСЛИТЕЛЬНАЯ МОДЕЛЬ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ПРИБЛИЖЕННЫМИ ИСХОДНЫМИ ДАННЫМИ НА ОСНОВЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ВОЛЬТЕРРЫ ВТОРОГО РОДА»

Известия Кабардино-Балкарского научного центра РАН № 4 (102) 2021

ИБС: 39А60; 39В42

ВЫЧИСЛИТЕЛЬНАЯ МОДЕЛЬ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С ПРИБЛИЖЕННЫМИ ИСХОДНЫМИ ДАННЫМИ НА ОСНОВЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ВОЛЬТЕРРЫ ВТОРОГО РОДА

, Е.П. ЯРЦЕВА, Л.В. АНДРУХИВ

Северо-Кавказский федеральный университет 355000, Ставропольский край, г. Ставрополь, пр. Кулакова, 2 E-mail: info@ncfu.ru

В математических моделях физических явлений, использующих результаты экспериментов, зачастую возникает необходимость решения дифференциальных уравнений. Подобные задачи относятся к классу некорректных математических задач. В данной работе для получения приближенного решения дифференциального уравнения первого порядка с определенными краевыми условиями выполняется построение соответствующего регуляризирующего алгоритма. Реализуется метод, заключающийся в построении эквивалентного исходному дифференциальному уравнению интегрального уравнения Вольтерры второго рода. Для его численного решения приводится вычислительный алгоритм, позволяющий получать устойчивые решения некорректной задачи.

Ключевые слова: дифференциальное уравнение, интегральное уравнение Вольтерры второго рода, итерационная вычислительная схема, вычислительный алгоритм.

Поступила в редакцию 30.04.2021

Для цитирования. Наац В.И., Ярцева Е.П., Андрухив Л.В. Вычислительная модель для дифференциального уравнения с приближенными исходными данными на основе интегрального уравнения Вольтерры второго рода // Известия Кабардино-Балкарского научного центра РАН. 2021. № 4(102). С. 5-16.

Многие научные исследования посвящены вопросам численного решения некорректных задач, в том числе решению дифференциальных уравнений с приближенными исходными данными, о чем свидетельствуют, например, монографии 1. Из современных публикаций по данному научному направлению известны работы 8. В работах ряда авторов 11 излагаются вопросы приложений интегральных уравнений Фредгольма для краевых задач. Кроме приведенных работ, существуют и многие другие, развивающие данное научное направление, являющееся современным и актуальным в области вычислительной математики.

Постановка задачи и подходы к ее решению. В работе [9] изложен подход и соответствующий итерационный метод, который далее приведем в сокращенном виде для большей наглядности. Рассматривается дифференциальное уравнение вида

где г е[го, Т], и(го ) задано и функционал Е(г, и) непрерывен и ограничен на множестве возможных решений и с С. Правая часть в (1) представлена своим с- приближением ^(г,и), в результате возникает проблема устойчивости приближенных решений и(г)

при наличии ошибок в исходных данных. Альтернативным подходом к построению решающего алгоритма является замена функционального уравнения (1) приближенным или «близким» к нему, например, уравнением вида

u'(t) + а ■ u(t) = F (t, u), (2)

где параметр модели а > 0 — достаточно малая величина, и выбор значений а с учетом ожидаемой величины погрешности с реализуется в вычислительном эксперименте. При построении вычислительного алгоритма для уравнения (2) используется интегральное уравнение Вольтерры второго рода

u(t) = J e T-t0 ■F (t’, u(t’))dt’ + u(t0) ■ e T-t0. (3)

Наличие множителя exp^ — а—^ в уравнении (3) выражает стабилизирующее

действие на сходимость последовательности приближенных решений

Kn (х, х ‘) = Kw (х — х ‘) = Kw (|х — х ‘ |) — 0 при |х — х ‘ | —да. (5)

Очевидно, что <(Knf )(х)>— f (х) в слабом смысле в каждой точке х е Q. В соответствии с этим полагаем, что исследуемая функция f (х) представляется аппроксимирующей последовательностью <(Knf )(х)>или интегралом (4) при условии (5). Такие представления с практической точки зрения имеют интерес для тех ситуаций, когда f( х)

представлена своим с -приближением f (х), вектором приближенных значений f размерности m либо приближенным уравнением. В работе исследуются такие представления функций интегралами Вольтерры, в которых соотношения (4) принимают вид

J En (t, t’ )■ u (t’ )dt’ = un (t) = (Enu Xt),

limu (t) = u(t), (t ‘ 0), который примем как d = T —10. В работе [ 1 ] показано, что En(t,t’) приn = 1,2. удовлетворяет условиям (5) для Vu(t) е Cz(Qf), а также доказана справедливость основного предельного соотношения

limun (t) = lim(Eu )(t) = u(t), (8)

Vt е Q = [t0, T], когда Ew (t, t’) определяется выражением (7). Использование изложенного выше аппарата аппроксимации функции в задачах численного решения дифференциальных уравнений требует построения аналогичных аппроксимирующих последовательностей для производных функций, входящих в эти уравнения. Если в точке t e[t0, T]

функция u(t) имеет ограниченную производную, то аналогично (6):

(EU Xt )=iEn (t, t’ У (t’ )dt’ = (u )„ (t),

lim (u’)n (t)= U(t), t’ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

У = 1,2. с начальным приближением м(0)(1) = ((1). Для рассматриваемого уравнения

(12) с ядром К(1, у) = е Я (Я = (т • Т) 1) можно найти итерированное ядро, то есть вы-

числить функциюКт(1,у) = |Кт-1(1,у’)К(у’,у)йу’, т = 1,2. В результате итераци-

онный процесс (12) сводится к вычислению интеграла

Если ((1) зависит от и(1), в вычислительной схеме вместо ((1) фигурирует ((1, и(у 1)) . Очевидно, что для сходимости последовательностей приближенных решений

|и (у)(1 необходимы непрерывность и ограниченность частных производных ((1, и) по

соответствующим переменным (условия Коши).

Технику построения итерационной схемы (12) и анализ ее сходимости для уравнения (11) приведем ниже. В соответствии с (12) имеем

1 1 1—1 1_10 и(«)(1) = — • | е

Используя разностные соотношения, выражение (14) представим в виде

(д(у,у-1)и )(1) = — • ¡ е»^ •(д(у-1,у-2)Е )(1>’ + т • Т • (д(у-1,у-2 Е )(1). (15)

Для сходимости схемы (15) при у ^ те необходимо обеспечить выполнение неравенства (д(у,у-1)М)(1 ) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где С, = В, — кА’, и окончательный результат

11 (/)=1 С/, (Л = 0,1. т), (к 0)

n, тогда сетка <^ >т=0 предназначается для корректного вычисления

интегральных сумм в (21). С этой сеткой связан искомый вектор / размерности m. Будем считать, что узлы сетки являются равноотстоящими, и для ее определения достаточно найти числа к = ^ — (к = 0,1. т). Сетка >П=0является произвольной и определя-

М т1пр((/,/а)=р(Сг/*,/а) 0 — сколь угодно малое число.

Найденный из решения оптимизационной задачи (22) вектор f * применяется для построения аппроксимирующего аналога искомой функции f (t) на основе соответствующей интегральной суммы. Итак, согласно интегралу (Enf )(t) в (6)

f(tЬ f О[ T, hf • = f(t) (23)

для всех t е Q = [t0,T] (т* > 0). Решение f *(t), представленное некоторой непрерывной функцией, т. е. обобщенным полиномом порядка m в понятиях теории приближения, позволяет использовать термин «восстановление непрерывного хода (графика) f(t)».

Формально f (t) сходится к f (t) при т — 0 и h — 0 в слабом смысле, как это следует из соотношений (6). Тем не менее, если речь идет о непрерывности f (t) в каждой точке t е Qf, то можно говорить и о равномерной сходимости, о чем речь шла выше.

В заключение сделаем несколько замечаний относительно «восстановления производной» (Df )(t) искомой функции f (t) в условиях, когда известен вектор f * размерности т. В работе показано, что данную задачу можно решить на основе оператора обобщенного дифференцирования, так как если функция f (t) дифференцируема в точке t

и ее производная суммируема почти всюду в Q, то справедливо записать представление (Df )(t) в виде интегралов типа (6):

JEn (t, t %Df )f (t ‘)dt’ = (EnDf )(t )= (Df )n (t), t0 (24)

lim (Df )n (t ) = Df (t), t е Q.

При этом в качестве оператора обобщенного дифференцирования примем интегральный оператор вида

f (t )-(E,f Kf)- f (to) e

Если /(1) обладает непрерывной производной /'(1), то (ц/)(1) ^ (Ц/)(1) равномерно на О . В равенстве (25) интеграл (Ет/)?) для найденного вектора / * представляется интегральной суммой (23).

Заключение. Изложенный в статье алгоритм требует реализации в вычислительном эксперименте, разработки соответствующих тестовых задач и получения на их основе численных решений с анализом полученных результатов. Это большая работа, которой будут посвящены дальнейшие исследования авторов.

1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.

2. Наац И.Э., Зуев В.Е. Обратные задачи оптики атмосферы. Л.: Гидрометеоиздат, 1990. 270 с.

3. Zuev V.E., Naats I.E. Inverse Problems of Lidar Sensing of the Atmosphere. SpringerVerlag Berlin Heidelberg New York. 1983. 260 p.

4. Митрохин С.И. Периодическая краевая задача для дифференциального оператора четвертого порядка с суммируемым потенциалом // Владикавказский математический журнал. 2017. № 4. Том 19. С. 35-49.

5. Расолько Г.А., Шешко С.М., Шешко М.А. Об одном методе численного решения некоторых сингулярных интегро-дифференциальных уравнений // Дифференциальные уравнения. 2019. № 9. Том 55. С. 1285-1292.

6. Табаринцева Е.В. О решении некорректно поставленной задачи для нелинейного дифференциального уравнения // Труды института математики и механики УРО РАН. 2015. № 1. Том 21. С. 231-237.

7. Матысик О.В. Неявный итерационный метод решения несамосопряженной некорректной задачи с приближенным оператором и приближенно заданной правой частью // Вестник Гродненского государственного университета им. Янки Купалы. 2015. № 3. С. 75-82.

8. Gulin A.V., Morozova V.A. On the Stability of Nonlocal Difference Schemes in Subspaces // Differential Equations. 2014. Vol. 50, № 7. Pp. 888-898.

9. Наац И.Э., Наац В.И. Представление функций и их производных интегралами Воль-терры в численных методах решения дифференциальных уравнений // Вестник Ставропольского государственного университета. 2011. Выпуск 75(4). С. 5-13.

10. Наац И.Э., Наац В.И., Рыскаленко Р.А. Вычислительная модель для дифференциального уравнения с эмпирическими функциями на основе интегрального уравнения Фредгольма первого рода // Наука. Инновации. Технологии: научный журнал СевероКавказского федерального университета. 2016. Выпуск № 2. С. 37-48.

11. Наац В.И., Рыскаленко Р.А., Ярцева Е.П. Обратные задачи и качественные модели в проблеме мониторинга атмосферы. LAP LAMBERT Academic Publishing. 2015. 405 с.

1. Tikhonov A.N., Arsenin V.Ya. Metody resheniya nekorrektnykh zadach [Methods for solving incorrect (ill-posed) problems]. M.: Science. 1979. 288 p.

2. Naats I.E., Zuev V.E. Obratnyye zadachi optiki atmosfery [Inverse problems of atmospheric optics]. L.: Gidrometeoizdat. 1990. 270 p.

3. Zuev V.E., Naats I.E. Inverse Problems of Lidar Sensing of the Atmosphere. SpringerVerlag Berlin Heidelberg New York. 1983. 260 p.

4. Mitrokhin S.I. Periodicheskaya krayevaya zadacha dlya differentsial’nogo operatora chetvertogo poryadka s summiruyemym potentsialom [Periodic boundary value problem for a fourth-order differential operator with a summable potential] // Vladikavkaz Mathematical Journal. 2017. No. 4. Vol. 19. Pp. 35-49.

5. Rasolko G.A., Sheshko S.M., Sheshko M.A. On one method of numerical solution of some singular integro-differential equations // Differential Equations. 2019. No. 9. Volume 55. Pp.1285-1292.

6. Tabarintseva E.V. O reshenii nekorrektno postavlennoy zadachi dlya nelineynogo differ-entsial’nogo uravneniya [On the solution of an ill-posed problem for a nonlinear differential equation] // Trudy instituta matematiki i mekhaniki URO RAN [Proceedings of the Institute of Mathematics and Mechanics URO RAS]. 2015. No. 1. Volume 21. Pp. 231-237.

7. Matysik O.V. Neyavnyy iteratsionnyy metod resheniya nesamosopryazhennoy nekor-rektnoy zadachi s priblizhennym operatorom i priblizhenno zadannoy pravoy chast’yu [An implicit iterative method for solving a non-self-adjoint ill-posed problem with an approximate operator and an approximately given right-hand side] // Vestnik Grodnenskogo gosudarstvennogo universiteta im. Yanki Kupaly [Bulletin of the Grodno State University n.a. Yanko Kupala]. 2015. No. 3. Pp. 75-82.

8. Gulin A.V., Morozova V.A. On the Stability of Nonlocal Difference Schemes in Subspaces // Differential Equations. 2014. Volume 50. № 7. Pp. 888-898.

9. Naats I.E., Naats V.I. Predstavleniye funktsiy i ikh proizvodnykh integralami Vol’terry v chislennykh metodakh resheniya differentsial’nykh uravneniy [Representation of functions and their derivatives by Volterra integrals in numerical methods for solving differential equations] // Vestnik Stavropol’skogo gosudarstvennogo universiteta [Bulletin of the Stavropol State University]. 2011. Issue 75 (4). Pp. 5-13.

10. Naats I.E., Naats V.I., Ryskalenko R.A. Vychislitel’naya model’ dlya differentsial’nogo uravneniya s empiricheskimi funktsiyami na osnove integral’nogo uravneniya Fredg-ol’ma pervogo roda [Computational model for a differential equation with empirical functions based on the Fredholm integral equation of the first kind] // Nauka. Innovatsii. Tekhnologii: Nauchnyy zhurnal Severo-Kavkazskogo federal’nogo universiteta [Science. Innovation. Technologies»: Scientific journal of the North Caucasus Federal University]. Issue No. 2. 2016. Pp. 37-48.

11. Naats V.I., Ryskalenko R.A., Yartseva E.P. Obratnyye zadachi i kachestvennyye modeli v probleme monitoringa atmosfery [Inverse problems and qualitative models in the problem of atmospheric monitoring] LAP LAMBERT Academic Publishing. 2015. 405 p.

COMPUTATIONAL MODEL FOR A DIFFERENTIAL EQUATION WITH APPROXIMATE INITIAL DATA BASED ON THE VOLTERRA INTEGRAL EQUATION OF THE SECOND KIND

, E.P. YARTSEVA, L.V. ANDRUKHIV

North Caucasus Federal University 355000, Stavropol Territory, Stavropol, Kulakov Ave., 2 E-mail: info@ncfu.ru

In mathematical models of physical phenomena that use the results of experiments, it is often necessary to solve differential equations. Such problems belong to the class of incorrect mathematical problems. In this paper, to obtain an approximate solution of a first-order differential equation with certain boundary conditions, the corresponding regularizing algorithm is constructed. A method is implemented that consists in constructing a Volterra integral equation of the second kind equivalent to the original differential equation. For its numerical solution, we present a computational algorithm that allows us to obtain stable solutions to an ill-posed problem.

Keywords: differential equation, Volterra integral equation of the second kind, iterative computational scheme, computational algorithm.

Received by the editors 30.04.2021

For citation. Naats V.I., Yartseva E.P., Andrukhiv L.V. Computational model for a differential equation with approximate initial data based on the Volterra integral equation of the second kind // News of the Kabardino-Balkarian Scientific Center of RAS. 2021. No. 4 (102). Pp. 5-16.

Сведения об авторах:

Наац Виктория Игоревна, д.ф.-м.н., профессор, кафедра математического моделирования СевероКавказского федерального университета, институт математики и информационных технологий им. проф. Н.И. Червякова.

355000, Ставропольский край, г. Ставрополь, пр. Кулакова, 2.

Ярцева Елена Павловна, к.ф.-м.н., доцент, кафедра математического моделирования Северо-Кавказского федерального университета, институт математики и информационных технологий им. проф. Н.И. Червякова. 355000, Ставропольский край, г. Ставрополь, пр. Кулакова, 2. E-mail: yartseva_elena@mail.ru

Андрухив Людмила Викторовна, к.пед.н., доцент, кафедра математического моделирования СевероКавказского федерального университета, институт математики и информационных технологий им. проф. Н.И. Червякова.

355000, Ставропольский край, г. Ставрополь, пр. Кулакова, 2. E-mail: lvandruhiv@mail.ru

Information about the authors:

Naats Viktoria Igorevna, Doctor of Physics and Mathematics, Professor, Department of Mathematical Modeling, North Caucasus Federal University, Institute of Mathematics and Information Technologies named after prof. . N.I. Chervyakov.

355000, Stavropol Territory, Stavropol, Kulakov Ave., 2.