Уравнение регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 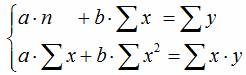
Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.
Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:
Построение линейной однофакторной регрессионной модели зависимости результативного признака Y от фактора Х.
Линейное однофакторное уравнение регрессии имеет вид:
Коэффициенты уравнения регрессии вычисляются по формулам:
Для расчета коэффициентов строится вспомогательная табл.2.2
(расчеты проведены с применением пакета MS Excel):
Расчетная таблица для построения и анализа
Линейной модели парной регрессии
| №п/п | 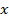 |  |  |  | xy |  |  |  |
| 2175,181 | 357,21 | 94,459 | ||||||
| 2177,631 | 357,21 | 52,838 | ||||||
| 2177,631 | 320,41 | 52,838 | ||||||
| 2180,081 | 62,41 | 23,222 | ||||||
| 2180,081 | 24,01 | 23,222 | ||||||
| 2180,081 | 166,41 | 23,222 | ||||||
| 2180,081 | 98,01 | 23,222 | ||||||
| 2180,081 | 118,81 | 23,222 | ||||||
| 2182,531 | 8,41 | 5,612 | ||||||
| 2182,531 | 4,41 | 5,612 | ||||||
| 2182,531 | 50,41 | 5,612 | ||||||
| 2182,531 | 8,41 | 5,612 | ||||||
| 2182,531 | 0,01 | 5,612 | ||||||
| 2182,531 | 9,61 | 5,612 | ||||||
| 2182,531 | 16,81 | 5,612 | ||||||
| 2182,531 | 4,41 | 5,612 | ||||||
| 2182,531 | 26,01 | 5,612 | ||||||
| 2182,531 | 8,41 | 5,612 | ||||||
| 2184,981 | 4,41 | 0,006 | ||||||
| 2184,981 | 292,41 | 0,006 | ||||||
| 2184,981 | 4,41 | 0,006 | ||||||
| 2184,981 | 4,41 | 0,006 | ||||||
| 2187,431 | 26,01 | 6,406 | ||||||
| 2189,881 | 65,61 | 24,81 | ||||||
| 2189,881 | 50,41 | 24,81 | ||||||
| 2189,881 | 50,41 | 24,81 | ||||||
| 2194,781 | 50,41 | 97,634 | ||||||
| 2197,231 | 146,41 | 152,053 | ||||||
| 2197,231 | 50,41 | 152,053 | ||||||
| 2204,581 | 102,01 | 387,342 | ||||||
| Всего | 65546,98 | 2488,7 | 1242,317 | |||||
| Среднее | 2321,67 | 2184,9 | 4773870,967 | 5072782,467 | — | 82,956 | 41,41 |
Расчет коэффициентов уравнения регрессии на основе данных табл.2.2:


Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения
Коэффициент регрессии 

3. Проверка уравнения регрессии на адекватность[2].
1. Оценка практической пригодности построенной модели связи

Расчет R 2 :
Вывод. Критерий практической пригодности модели связи R 2 > 0,5 не выполняется. Однако поскольку значение R 2 практически совпадает с 0,5, можно считать, что построенное регрессионное уравнение в достаточной мере отражает фактическую зависимость признаков и пригодно для практического применения.
2. Оценка статистической значимости (неслучайности) коэффициента R 2 по F-критерию Р.Фишера рассчитывается по формуле:
где m – число коэффициентов уравнения регрессии (параметров уравнения регрессии), n- число наблюдений.
Расчет значения F при n=30, m=2:

Табличное (критическое) значение F-критерия Fтабл имеет общий вид 


Так как Fрасч>Fтабл, то величина найденного коэффициента детерминации R 2. признается неслучайной с вероятностью 0,95.
Вывод. Построенное уравнение регрессии
можно считать адекватным с надежностью 95%.
ПОСТРОЕНИЕ ОДНОФАКТОРНОГО УРАВНЕНИЯ РЕГРЕССИИ
Читайте также:
|
│►12. Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда у от стажа работы х по данным табл. 4. (10 рабочих одной бригады заняты производством радиоэлектронных изделий, данные ранжированы по стажу их работы). Исходя из экономических соображений стаж работы выбран в качестве независимой переменной х. Сопоставление данных параллельных рядов признаков х и у показывает, что с возрастанием признака х (стажа работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует прямая зависимость, пусть неполная, но выраженная достаточно ясно. Таблица 13 Распределение рабочих бригады по выработке и стажу работы
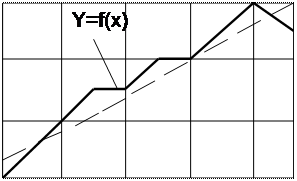
Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, у, получим корреляционное поле, а соединив их отрезками, — ломаную регрессии* (рис. 3). Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 3), которая может быть выражена простым линейным уравнением регрессии: где Данный метод эффективен лишь при небольшом объеме совокупности и достаточно тесной связи между признаками. Более наглядную характеристику связи можно получить, построив ломаную регрессии по частным средним.
1 3 5 7 9 х, годы Рис.3. Зависимость выработки одного рабочего у от стажа работы х (по данным табл.13) Пользуясь расчетными значениями (табл. 13), исчислим параметры для данного уравнения регрессии: Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного простого уравнения регрессии: Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значения у, найденные по данному уравнению, приведены в табл.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм итогов граф по у и У табл.13 (при этом возможно некоторое расхождение вследствие округления расчетов). ◄ 4.2. ПРОВЕРКА АДЕКВАТНОСТИ РЕГРЕССИОННОЙ МОДЕЛИ Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции — пара метры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, на сколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Рассмотрим t-критерий Стьюдента. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.
│►13. Для проверки значимости коэффициентов регрессии исследуемого уравнения Рассмотрим вспомогательную таблицу (табл. 14). Расчетные значения, необходимые для исчисления
Средние квадратические отклонения (табл. 14): Расчетные значения t-критерия Стьюдента: По таблице распределения Стьюдента для Поскольку расчетное значение tрасч>tтабл, оба параметра а0, а1 признаются значимыми по величине). ◄ Можно провести экономическую интерпретацию параметров уравнения регрессии После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего, нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель). В Из уравнения следует, что возрастание на 1 год стажа рабочего приводит к увеличению им дневной выработки в среднем на 0,6 изделия (величина параметра а1). Для удобства интерпретации параметра а1 используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %: В рассматриваемом примере Следовательно, с возрастанием стажа работы на 1% следует ожидать повышения производительности труда в среднем на 0,45%. Этот вывод справедлив только для изучаемой совокупности рабочих при конкретных условиях работы. Если данная совокупность и условия работы типичны, то коэффициент регрессии может быть использован для нормирования и планирования производительности труда рабочих этой профессии. Имеет смысл вычислить остатки Анализируя остатки, можно сделать ряд практических выводов. Значение остатков (табл. 7) имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют выработки рабочих, обозначенные номерами: 5; 1; 4; 8; 7, поскольку их выработки отличаются наибольшими отклонениями. Тем самым выявляются передовые рабочие – номера 1; 8; 7, обеспечивающие наибольшее повышение средней выработки (наибольшие положительные остатки) и отстающие, требующие особого внимания рабочие – номера 5, 4 (наибольшие отрицательные остатки). В итоге положительные отклонения выработки большинства рабочих уравновешиваются отрицательными отклонениями небольшого числа рабочих, т.е. Дата добавления: 2014-12-23 ; просмотров: 206 ; Нарушение авторских прав источники: http://lektsii.org/12-24406.html http://lektsii.com/1-42081.html |





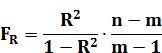



 (46)
(46)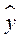 — теоретические значения результативного признака, полученные по уравнению регрессии;
— теоретические значения результативного признака, полученные по уравнению регрессии;  ,
, 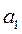 — коэффициенты (параметры) уравнения регрессии.
— коэффициенты (параметры) уравнения регрессии. от выравненных
от выравненных 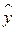 :
: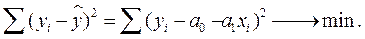 (47)
(47)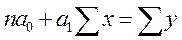 ; (48)
; (48)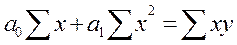 .
. ; (49)
; (49) . (50)
. (50)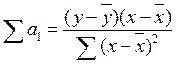 , (51)
, (51)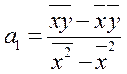 , (52)
, (52)
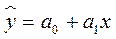 , находим значения
, находим значения 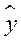 , зависящие только от заданного значения х [6].
, зависящие только от заданного значения х [6].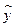
 =55
=55 =73
=73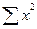 =385
=385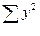 =565
=565 =451
=451
 — теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии; а0,а1 — неизвестные параметры уравнения регрессии; х — стаж работы рабочих, годы.
— теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии; а0,а1 — неизвестные параметры уравнения регрессии; х — стаж работы рабочих, годы.
 ;
;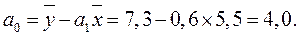


 =10-2 = 8 степенями свободы.
=10-2 = 8 степенями свободы. ,
, 

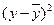


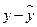




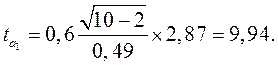
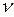 =8 находим критическое значение t-критерия: (tнабл=3,307 при α=0,05).
=8 находим критическое значение t-критерия: (tнабл=3,307 при α=0,05).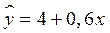 , характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр а1>0. Следовательно, с возрастанием стажа выработка увеличивается.
, характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр а1>0. Следовательно, с возрастанием стажа выработка увеличивается. (57)
(57) .
.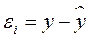 , характеризующие отклонение i-х наблюдений от значений, которые следует ожидать в среднем.
, характеризующие отклонение i-х наблюдений от значений, которые следует ожидать в среднем. .
.