Построить фундаментальную матрицу для систем уравнений

Системы линейных однородных уравнений

Назначение сервиса . Онлайн-калькулятор предназначен для нахождения нетривиального и фундаментального решения СЛАУ. Полученное решение сохраняется в файле Word (см. пример решения).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Свойства систем линейных однородных уравнений

Теорема. Система в случае m=n имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Теорема. Любая линейная комбинация решений системы также является решением этой системы.
Определение. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.

Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из ( n-r ) решений.

Однородные СЛАУ. Фундаментальная система решений

Однородные СЛАУ

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в матричном виде, $A X=\Theta$ всегда совместна, так как $X=\Theta$ всегда является ее решением.

Заметим, что если $x_<1>, x_<2>$ — это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=\lambda_ <1>x_<1>+\lambda_ <2>x_<2>$$ $$A Y=A\left(\lambda_ <1>x_<1>+\lambda_ <2>x_<2>\right)=\lambda_ <1>A x_<1>+\lambda_ <2>A x_<2>=\lambda_ <1>\Theta+\lambda_ <2>\Theta=\Theta$$

Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю.

Задание. Выяснить, имеет ли однородная СЛАУ $\left\<\begin 3 x-2 y=-1 \\ x+3 y=7 \end\right.$ ненулевые решения.

$$\Delta=\left|\begin 3 & -2 \\ 1 & 3 \end\right|=9-(-2)=9+2=11 \neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

Задание. Найти общее решение и ФСР однородной системы $\left\<\begin x_<1>+x_<2>-3 x_<4>-x_<5>=0 \\ x_<1>-x_<2>+2 x_<3>-x_<4>=0 \\ 4 x_<1>-2 x_<2>+6 x_<3>+3 x_<4>-4 x_<5>=0 \\ 2 x_<1>+4 x_<2>-2 x_<3>+4 x_<4>-7 x_<5>=0 \end\right.$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=\left(\begin 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end\right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end\right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end\right)$$

От четвертой строки отнимем $\frac<4><3>$ третьей и третью строку умножим на $\frac<1><3>$ :

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end\right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A \sim\left(\begin 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A \sim\left(\begin 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end\right)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>, x_<3>, x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

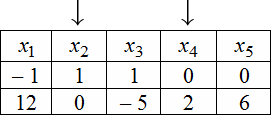
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $\left\<\begin x_<1>=-1+6 \cdot 0=-1 \\ x_<3>=1-\frac<5> <2>\cdot 0=1 \\ x_<5>=3 \cdot 0=0 \end\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что =12, x_<3>=-5, x_<5>=6> , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_<1>=\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right), X_<2>=\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>\left(\begin -1 \\ 1 \\ 1 \\ 0 \\ 0 \end\right)+C_<2>\left(\begin 12 \\ 0 \\ -5 \\ 2 \\ 6 \end\right)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Курсовая работа: Исследование методов решения системы дифференциальных уравнений с постоянной матрицей

2. Постановка задачи

3. Нахождение собственных чисел и построение ФСР

4. Построение фундаментальной матрицы решений методом Эйлера

5. Нахождение приближённого решения в виде матричного ряда

6. Построение общего решения матричным методом

7. Задача Коши для матричного метода

8. Решение неоднородной системы

Заключение

Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:

(1)

где коэффициенты а_ij , i=1,2,…. n, к=1,2,…,n, являются постоянными величинами;

y_i =y_i (t), i=1,2,…,n — неизвестные функции переменной t.

Если все b_i (t) (i=1,2,…,n) положить равным нулю (b_i (t)=0), то получится однородная система, соответствующая неоднородной системе (1).

Обозначая матрицу системы через А(х), а вектор через тогда систему (1) можем переписать в матричной форме

(1а)

Если , то получаем соответствующую систему однородных уравнений

. (2)

Всякая совокупность n функций

определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:

справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.

2. Постановка задачи

Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:

;;

Задание

1. Найти собственные числа и построить фундаментальную систему решений (ФСР).

2. Построить фундаментальную матрицу методом Эйлера.

3. Найти приближенное решение в виде матричного ряда.

4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.

5. Решить задачу Коши.

Вектор начальных условий: [1, 2, 3, 4]

3. Нахождение собственных чисел и построение ФСР

Однородной линейной системой дифференциальных уравнений называется система уравнений вида:

(3)

Если в матрице системы все =const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.

Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т.е. n линейно независимых решений этой системы.

Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.

Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:

(4)

Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.

Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY

Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:

Получилось два действительно корня и два комплексно-сопряженных корня . Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для и отдельно для . Запишем ФСР для данных для полученных характеристических чисел:

Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.

И общее решение системы будет выглядеть следующим образом:

Найдем решение данной системы с помощью метода Эйлера.

4. Построение фундаментальной матрицы решений методом Эйлера

Метод Эйлера заключается в следующем.

Решение системы (1) находится в виде:

(5)

Функция (5) является решением системы (1), если – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу . Если собственные значения ₁ , ₂ , … ,_n матрицы А попарно различны и a₁ , a₂ , …, a_n соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :

где С₁ , С₂ , … , С_n – произвольные числа.

Для случая кратных корней решение системы принимает вид

(6)

где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.

Если для кратного собственного значения матрицы А имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствует k независимых решений исходной системы:

Если для собственного значения кратности k имеется только m (m А , если ехр<А>.

Приближенно вектор решений можно найти как произведение матричного ряда:

Формула является матричной задачей Коши в приближенном виде.

Экспонентой матрицы А называется сумма ряда

где Е – единичная матрица.

Матрица является решением матричной задачи Коши:

т.е. является фундаментальной матрицей системы.

Найдем разложение матричного ряда последовательно по семи, восьми и десяти первым членам.

для получения разложения по 7 первым членам (аналогично по 8,10 и 10). Результатом будет являться матрица 4*4. Полученные матрицы умножаем на вектор начальных условий S=[1,2,3,4] и получаем приближенное решение в виде матричного ряда.

При увеличении членов разложения ряда вектор приближенных решений будет стремиться к вектору точных решений. Этот факт можно наблюдать, графически сравнивая изображение точного и приближенного решений (см. приложение).

Умножим на соответствующий вектор начальных условий и получим приближенное решение в виде матричного ряда, запишем полученное решение для n=7.

[s1 ≔ 1, s2 ≔ 2, s3 ≔ 3, s4 ≔ 4]

6. Построение общего решения матричным методом

Матричный метод решения системы уравнений (1) основан на непосредственном отыскании фундаментальной матрицы этой системы.

Экспонентой e A матрицы А называется сумма ряда

где Е – единичная матрица.

Свойство матричной экспоненты:

а) если АВ=ВА, то е А+В =е А *е В = е В *е А ;

б) если А=S — 1*B*S, то е А =S -1 *e B *S, где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных.

в) матрица y(t)=e At является решением матричной задачи Коши:

т.е. является фундаментальной матрицей системы (1).

Из свойства в) следует, что решение y(t) системы (1) удовлетворяющее условию y(0)=y₀ , определяется выражением y(t)=e At *y₀ . Таким образом, задача нахождения решений системы уравнений (1) эквивалентна задачи отыскания матрицы e At по матрице А.

Для вычисления матрицы e At удобно представить матрицу А в виде:

,

где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных, а B _А – жорданова форма матрицы А, т.к. e At = S -1 *e Bt *S.

Жорданова форма матрицы зависит от вида характеристических чисел.

1. Пусть характеристические числа действительные кратные, тогда Жорданова форма матрицы размерности nxn имеет вид:

где — действительный корень кратности n.

2. Если среди корней характеристического полинома имеются, как действительные разные, так и действительные кратные корни, то матрица В имеет вид:

где — действительные разные корни, а — действительный корень кратности 2.

3. При наличии среди корней характеристического полинома корней комплексно-сопряженных Жорданова клетка выглядит следующим образом:

где а комплексно сопряженный корень характеристического полинома.

Так как в нашем случае среди характеристических чисел присутствуют, как комплексно-сопряженные корни л = 2 —  ∨ л = 2 + , так и действительный разные корни л = -1 ∨ л = 1,то жорданова матрица выглядит следующим образом:

Из уравнения A_* S = S_* В, где S – невырожденная матрица, получаем систему 16-го порядка, из которой находим элементы матрицы S. Полученная матрица S будет выглядеть следующим образом:

Решаем систему 16-го порядка из уравнения A_* S = S_* В

Доопределяем некоторые элементы и получаем следующую матрицу S:

Значит матрица перехода найдена верно.

Для нахождения вектора решений y необходимо умножить матрицу S на , где — это вектор, элементы которого зависят от корней характеристического многочлена:

Для комплексных чисел имеет следующий вид:

Для случая корней действительных разных:

В нашем случае получается равной:

=

Отсюда найдем общее решение у=S*, получим:

При подстановке решения в исходную систему получается верное равенство, из этого следует, что решение найдено верно:

7. Задача Коши для матричного метода

Необходимо из всех решений системы уравнений найти такое решение, в котором y ( i ) (t) принимает заданное числовое значение y_{0 i} в заданной точке, т.е. найти значения с_i для следующих заданных значений: x=0, y=[1, 2, 3,4].

В вектор решений y(t) подставляем заданные условия и решаем полученную систему относительно c1, c2, c3, c4:

В результате получаем:

При подстановке c1, c2, c3, c4в общее решение получим решение в форме Коши:

Сделаем проверку, подставив общее решение в исходную систему

:

Получился нулевой вектор . Следовательно, найденная матрица является решением исходной системы.

Исследование зависимости жордановой формы матрицы А от свойств матрицы системы

Пусть J – жорданова клетка матрицы А. Для случая действительных разных корней жорданова клетка будет выглядеть следующим образом:

Пусть среди действительных собственных чисел матрицы А есть кратные. Жорданова клетка будет находиться по следующей формуле:

Например, если кратность k=2, то жорданову клетку матрицы мы можем записать так:

Если кратность k=3, то жорданову клетку матрицы мы можем записать так:

Если же среди трех собственных чисел являются корнями кратности 2, то жорданова форма будет выглядеть следующим образом:

Если два собственных числа матрицы А являются комплексными сопряженными, то запись жордановой клетки будет выглядеть так:

где – действительная, – мнимая часть собственного числа .

8. Решение неоднородной системы

Правая часть:

Общее решение неоднородной системы можно найти по формуле:

Где — фср, Со – матрица , F(t) – вектор правых части.

— общее решение однородной системы

— частное решение неоднородной системы

Полученное частное решение неоднородной системы:

Общее решение однородной системы

Тогда их сумма будет искомым общим решением неоднородной системы:

Найденное решение верно.

Изобразим графически точное частное решение однородной линейной системы дифференциальных уравнений с постоянными коэффициентами для начальных условий: t₀ = 0, y₀ = [1, 2, 3, 4].

Сравним график одной функции вектора точного решения и одной функции вектора приближенного решения с 3-мя, 5-ю и 7-ю членами ряда:

Где 1 – график приближенного решения для трех членов ряда; 2 – график приближенного решения для шести членов ряда; 3 – график приближенного решения для девяти членов ряда; 4 – график точного решения.

Можно сделать вывод:

С увеличением числа членов ряда, число совпадения членов ряда с точным решением будет увеличиваться, область совпадения будет расти.

Заключение

В ходе проделанной работы было изучено 3 метода нахождения общего решения однородной системы линейных дифференциальных уравнений: метод Эйлера, решение в виде матричного ряда и матричный метод. По сравнению с методом Эйлера и матричным методом, метод разложения в матричный ряд прост в реализации, но дает приближенное решение. Также была изучена задача Коши, которая была использована для нахождения частного решения однородной системы линейных дифференциальных уравнений для данного вида начальных условий.

Для установления правильности проведенных вычислений была проведена проверка с помощью подстановки полученных решений в исходную систему уравнений.

Для реализации этой работы в DERIVE были использованы следующие функции пакета:

1. EIGENVALUES (A, ) – вычисление собственных чисел матрицы A с последующей записью в вектор .

2. SOLVE (Pm=0, ) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0* m p1* m -1 +…+pm-1*+pm, а — переменная, относительно которой решается данное уравнение.

3. EXACT_VECTOR(A, ) – вычисление точного собственного вектора матрицы А и размещение этих значений в .

4. DIF(A,x,n) – дифференцирование A по xn раз.

5. SUM(M,n,f,g) – вычисление суммы M по n изменяющимся с f до g.

6. VECTOR(u,k,n)– задание (вычисление) вектора значений при k изменяющемся от 1 до n.

А также функции меню:

1. SOLVE/SYSTEM –решение системы с последующим заданием в диалоговом окне количества уравнений, самих уравнений и переменных, относительно которых решается данное уравнение.

2. Simplify > Expand– раскрытиевыражений.

Команда Expand используется для раскрытия математических выражений.

Expand expression: #n: где n – номер строки выражения (операнда).

Expand Variable: #n .

В этом варианте команды необходимо указать имя переменной, по которой будет проведено преобразование. Если по всем — .

3. Для построения графиков использовали функцию 2D-plot.