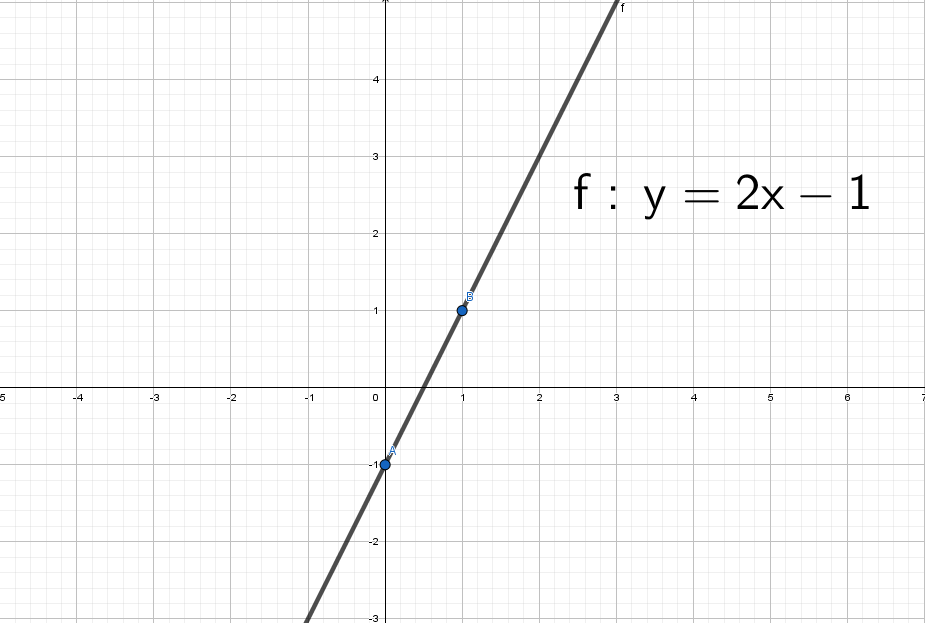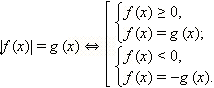Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
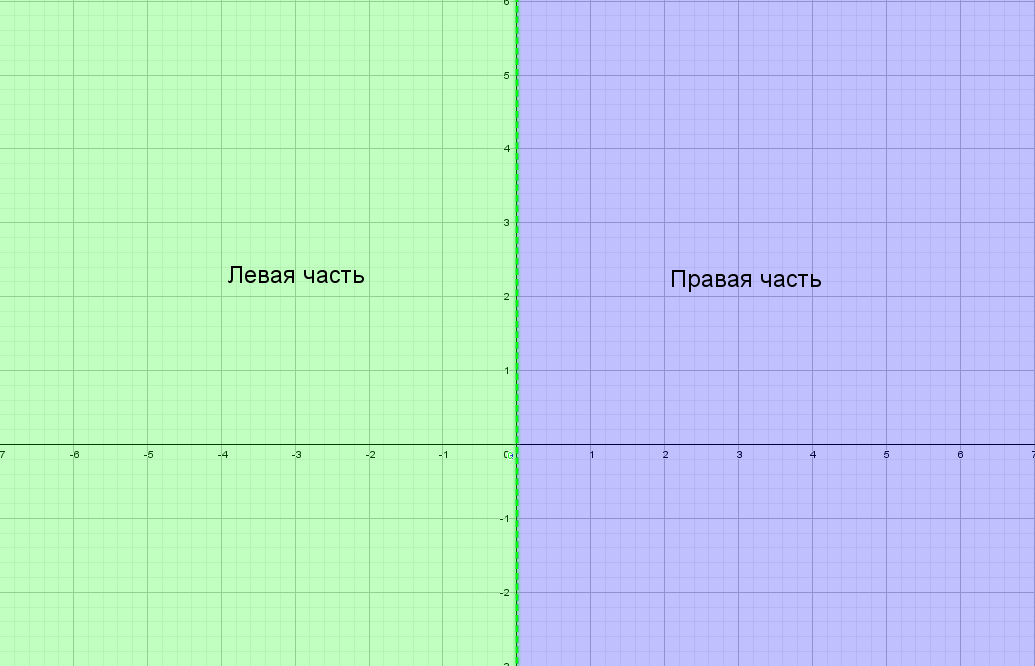
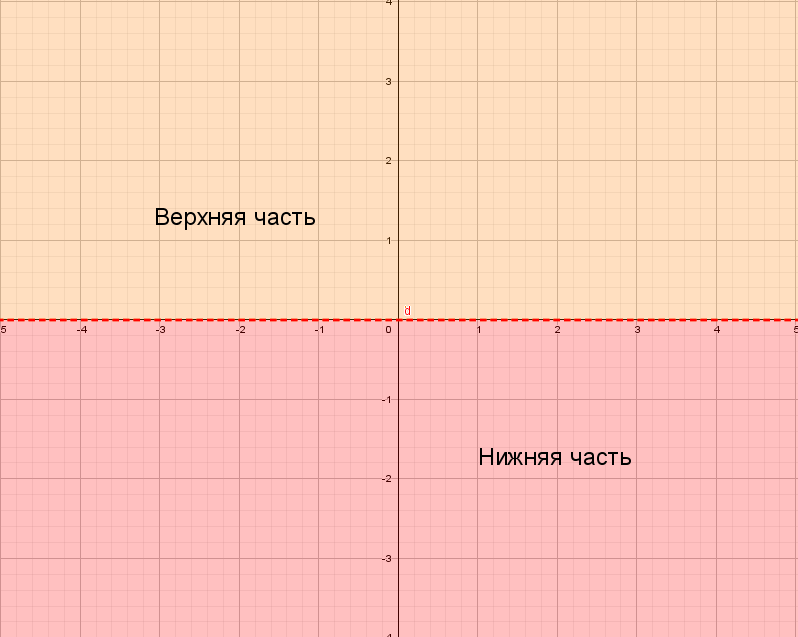
Для понимания друг друга введу немного «обзываний» системы координат:
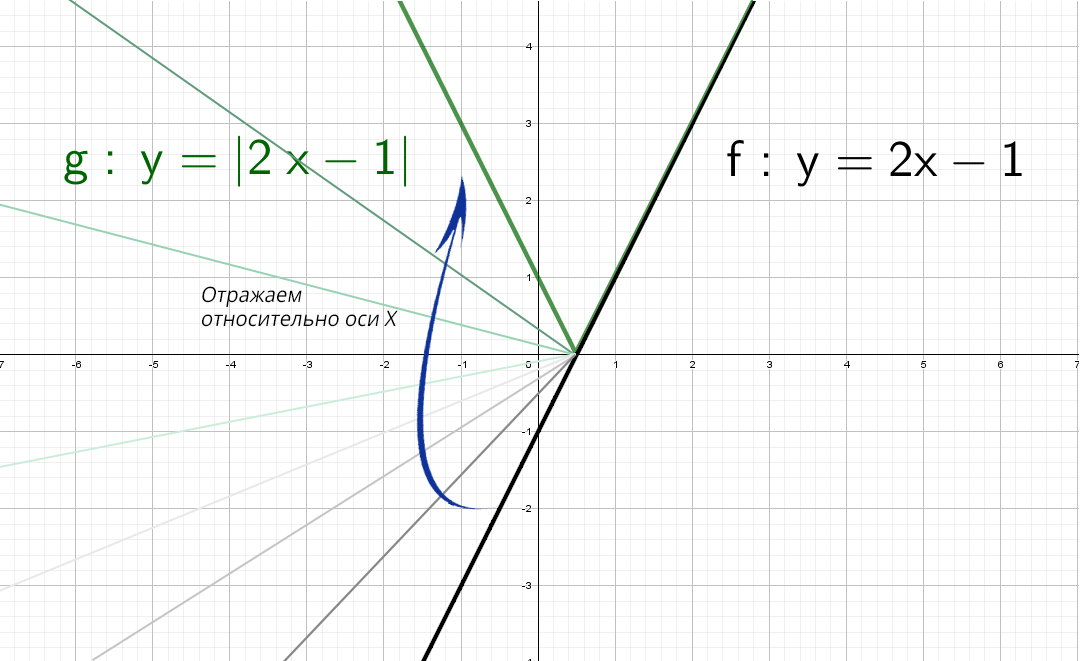
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
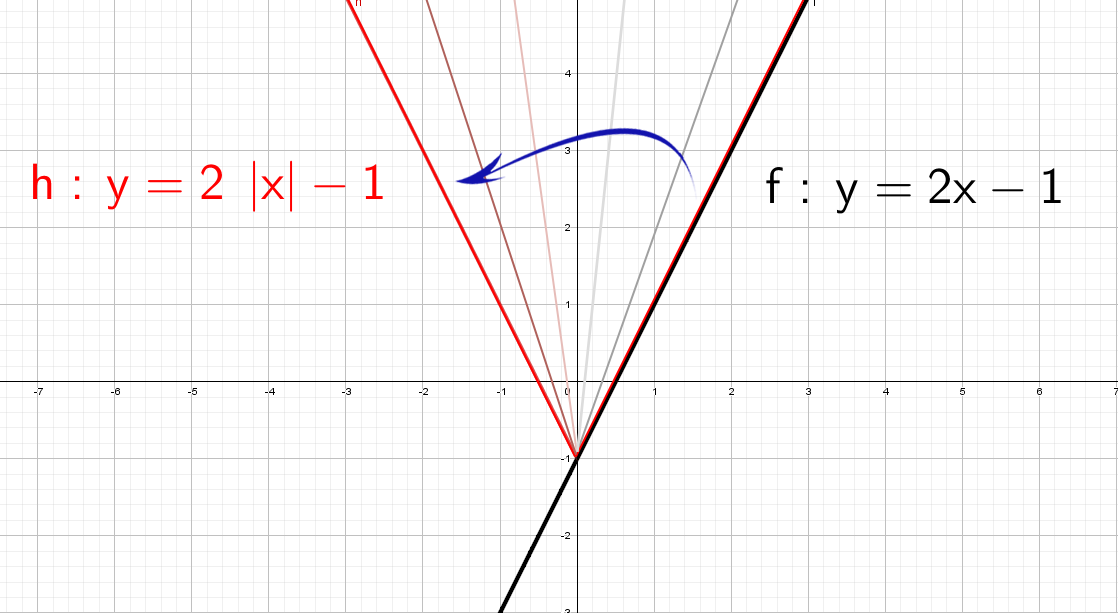
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение , получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
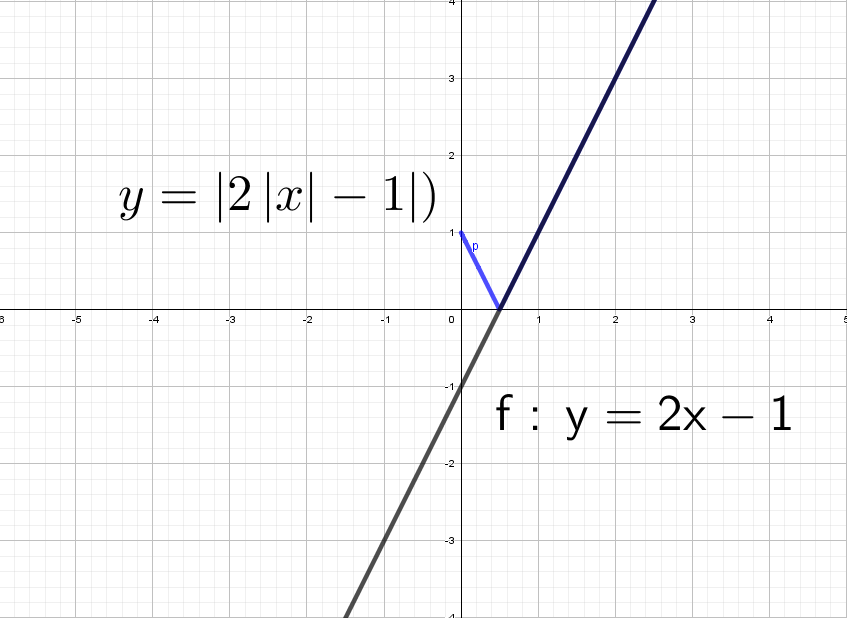
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
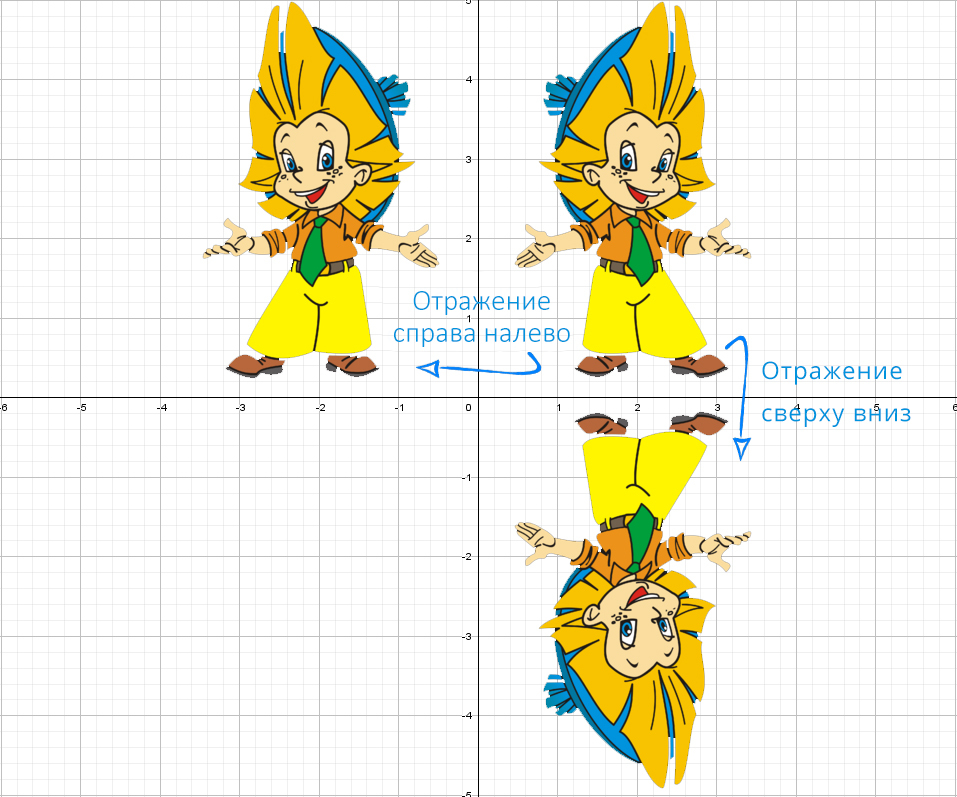
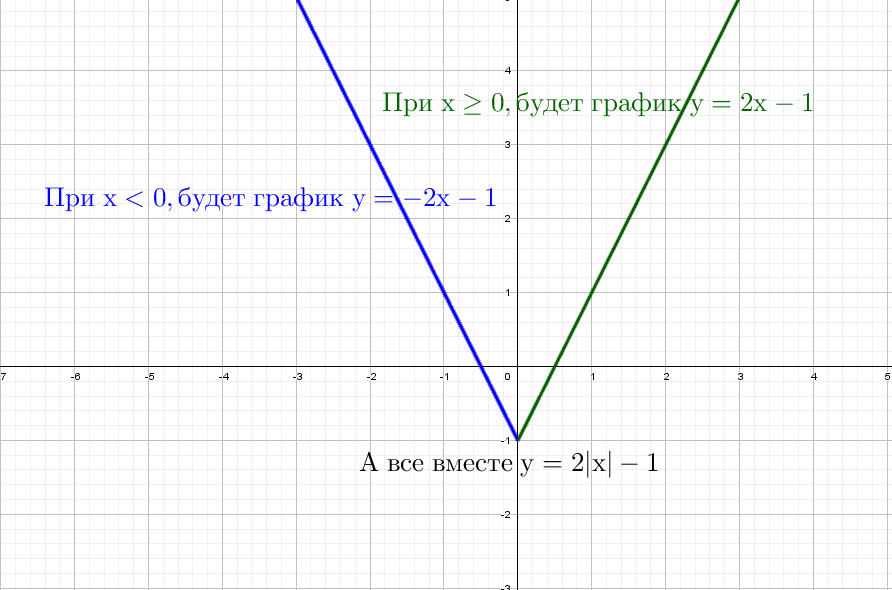
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y» . Такая же галочка, только теперь через другую ось.
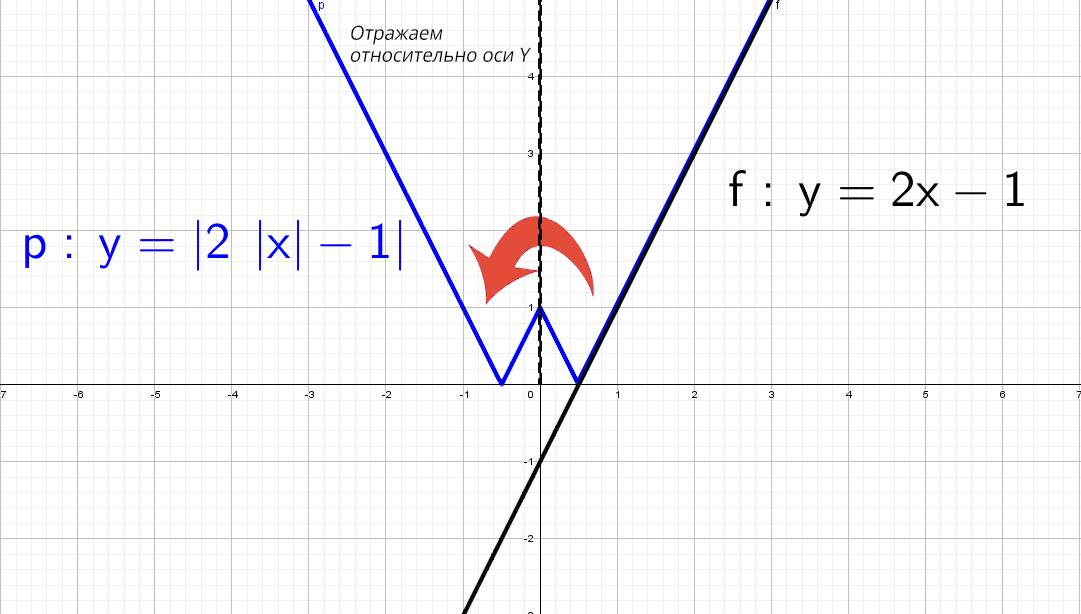
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
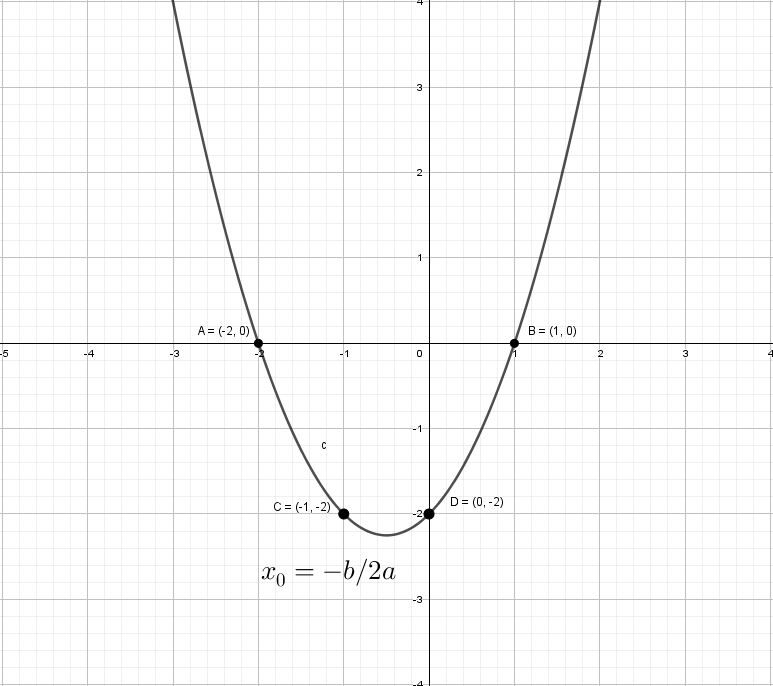
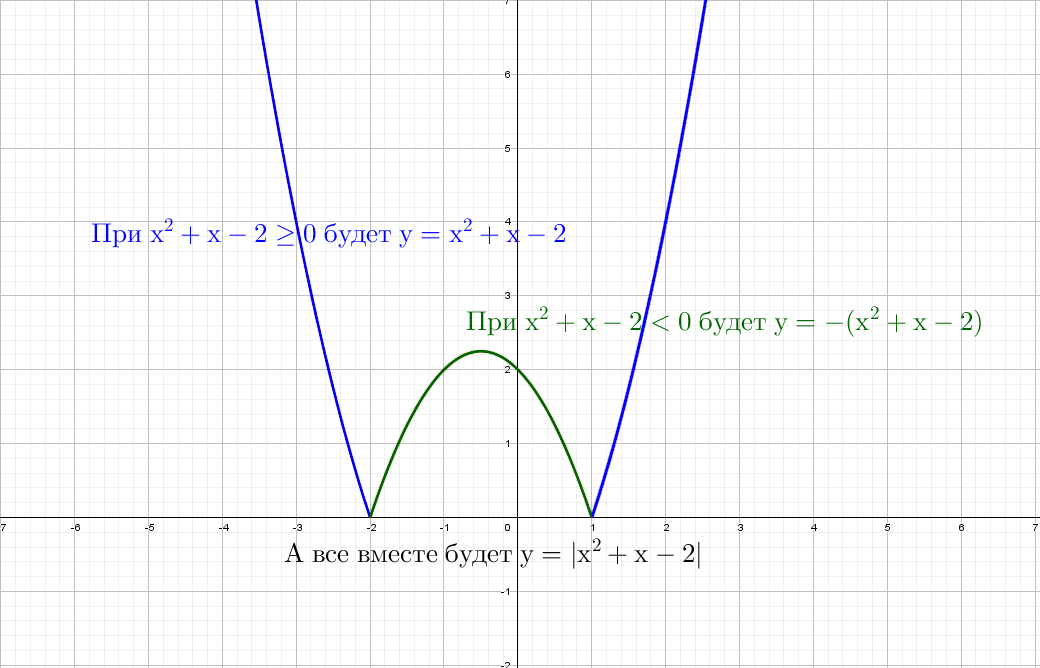
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x ₁ = 1 и x ₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
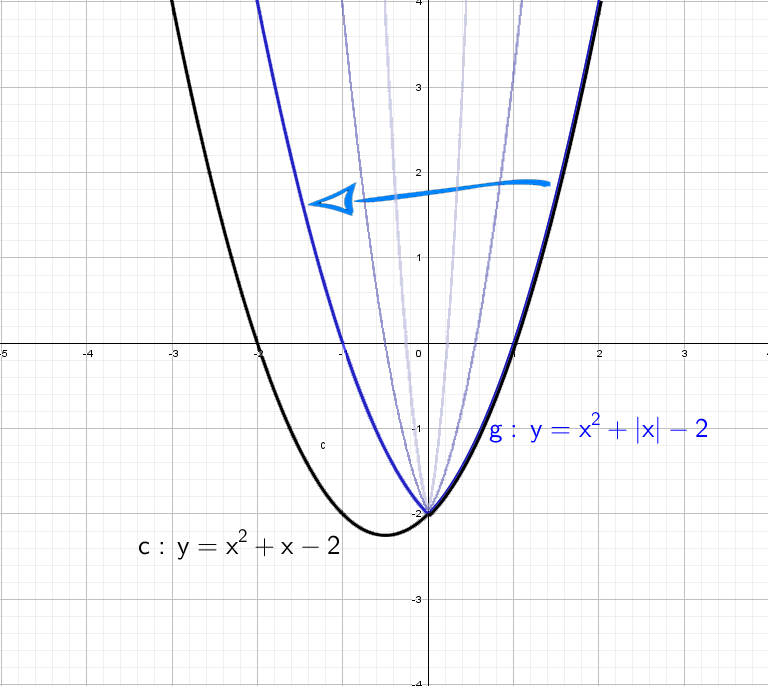
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
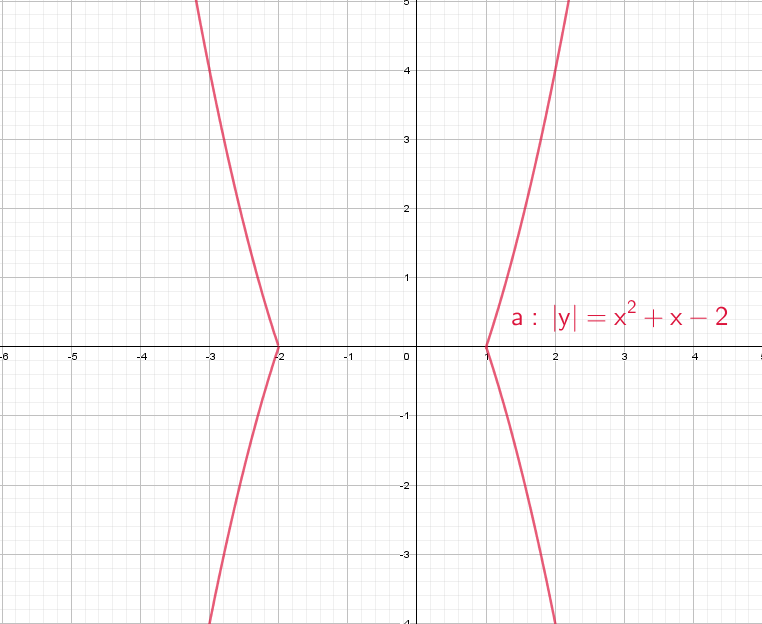
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
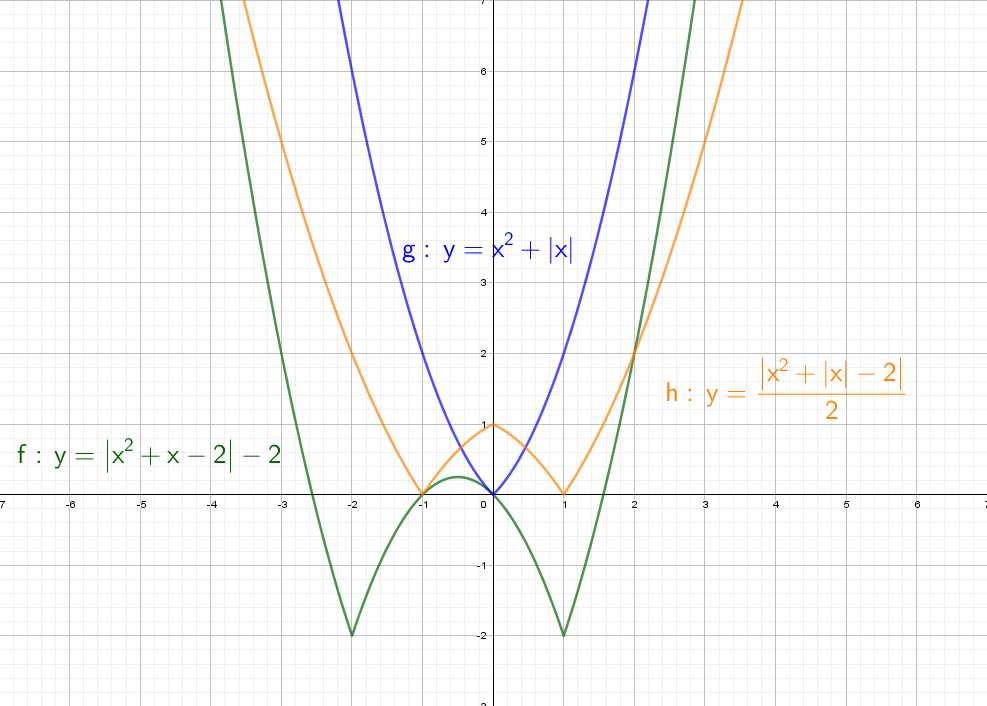
А теперь сразу комбо:
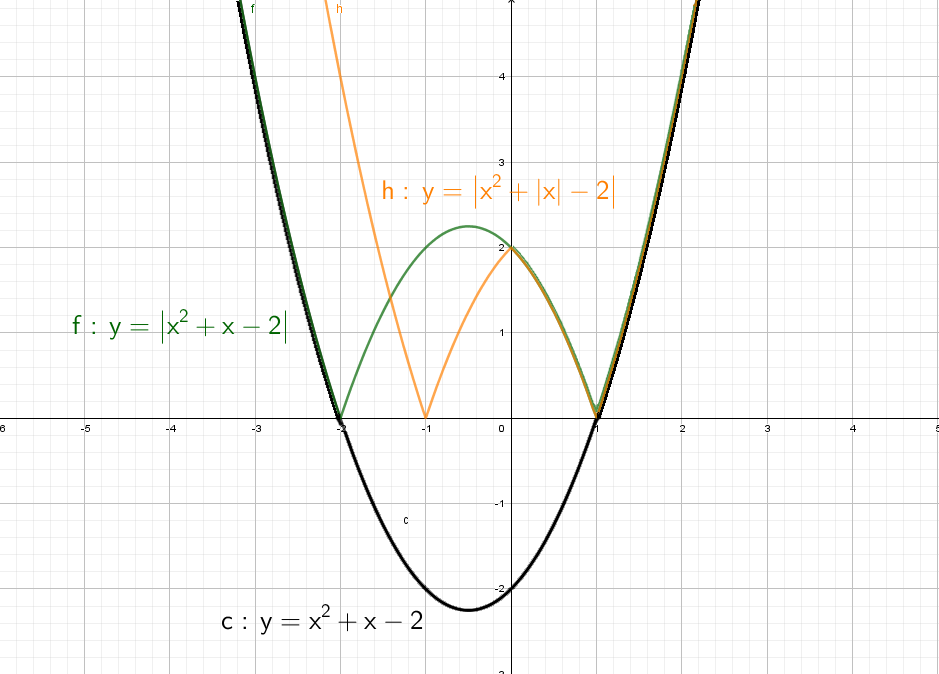
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум , потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
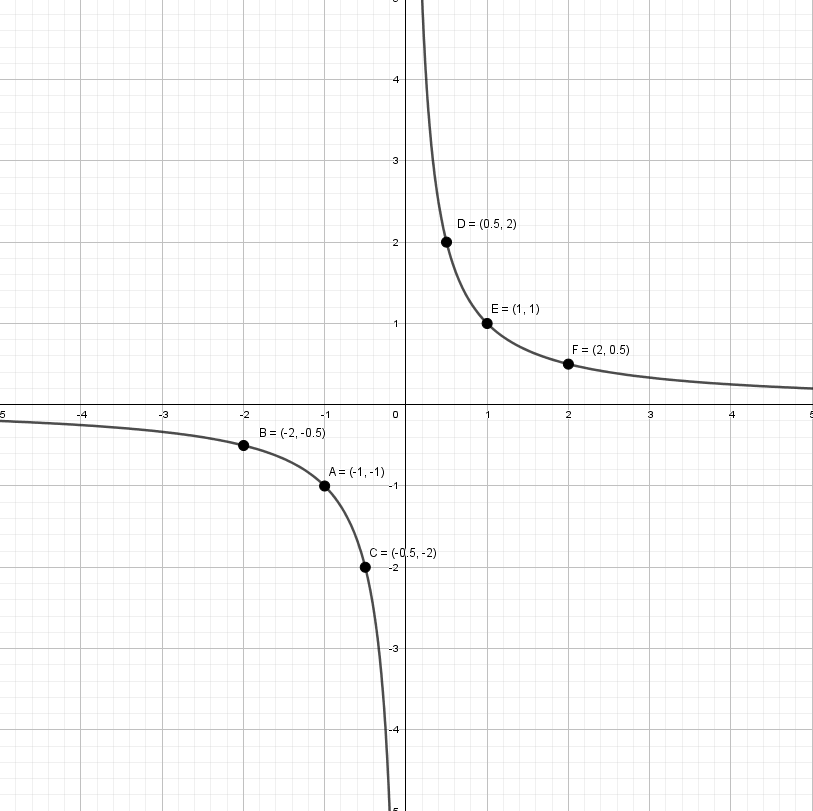
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
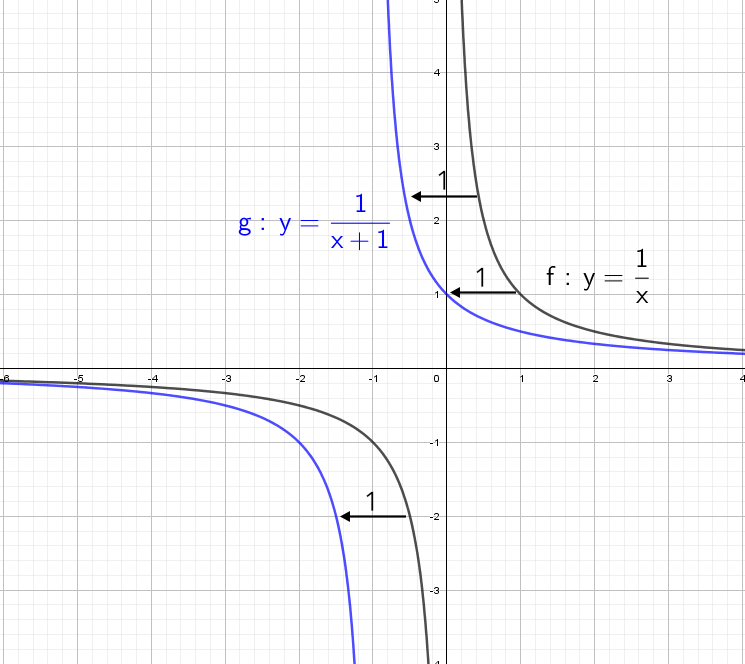
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.
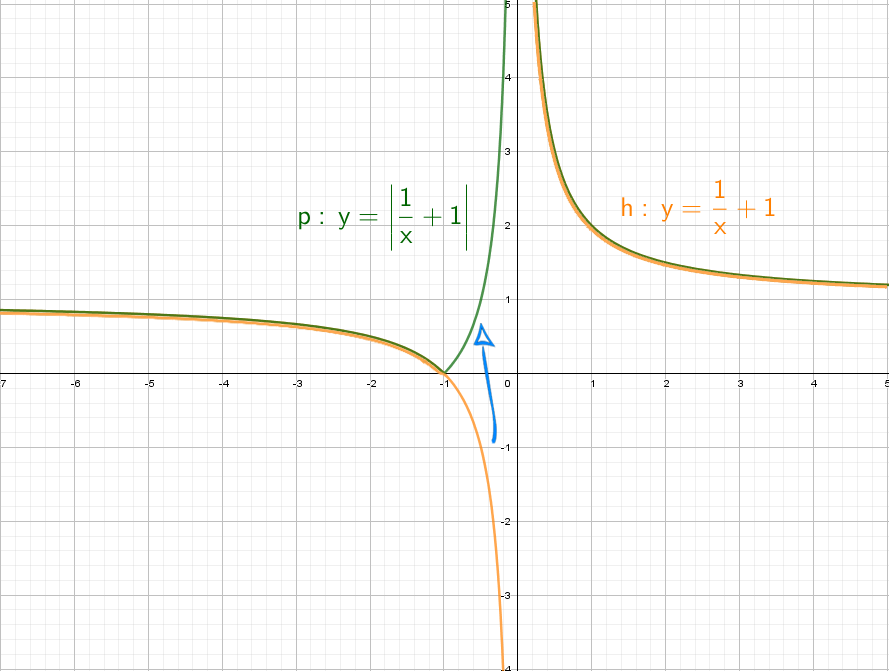
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
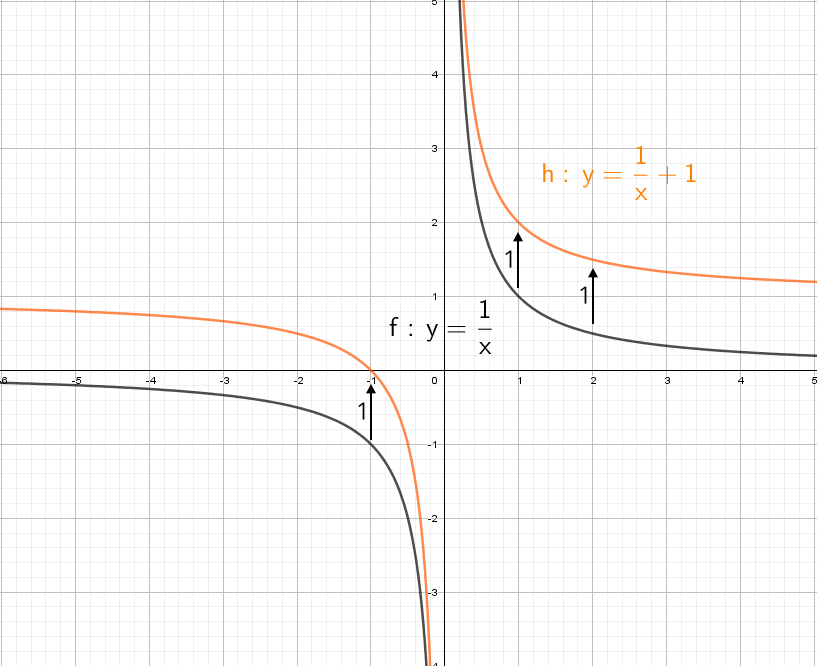
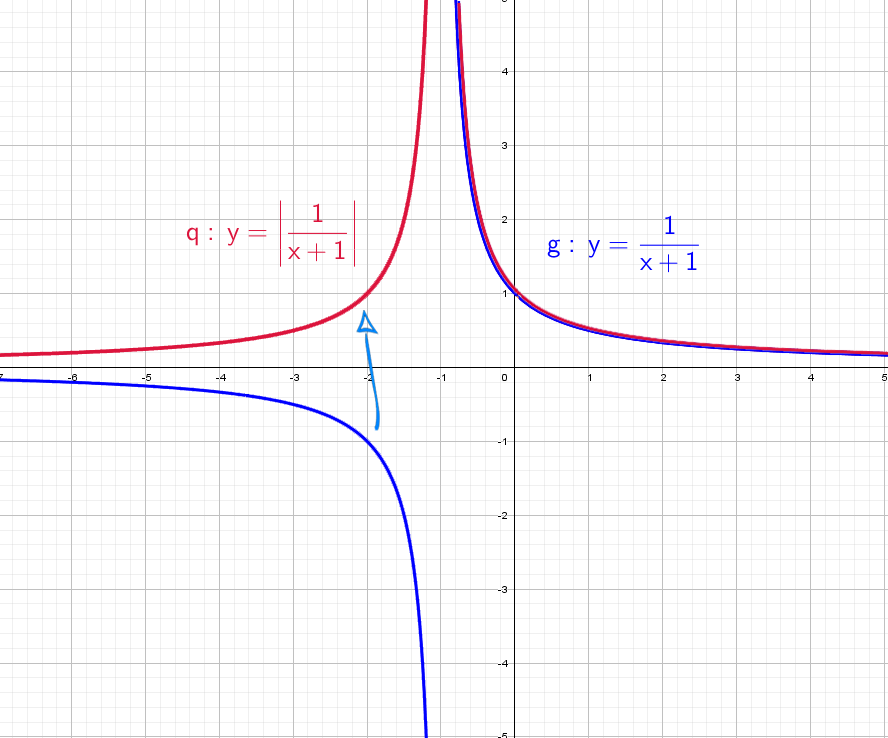
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
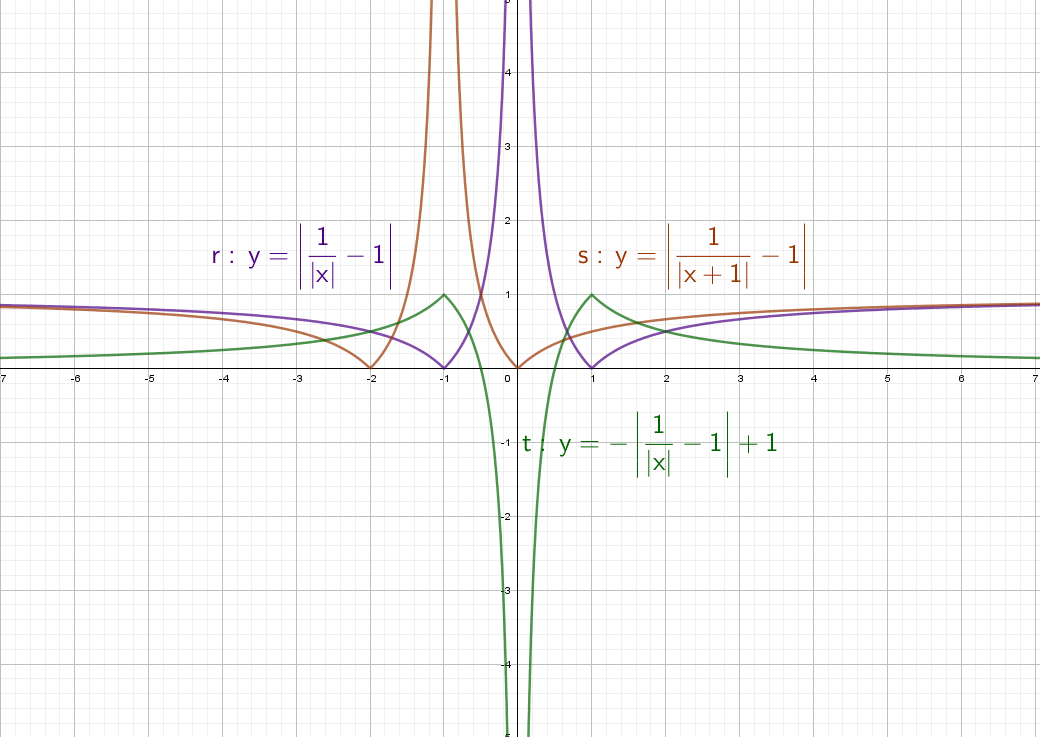
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
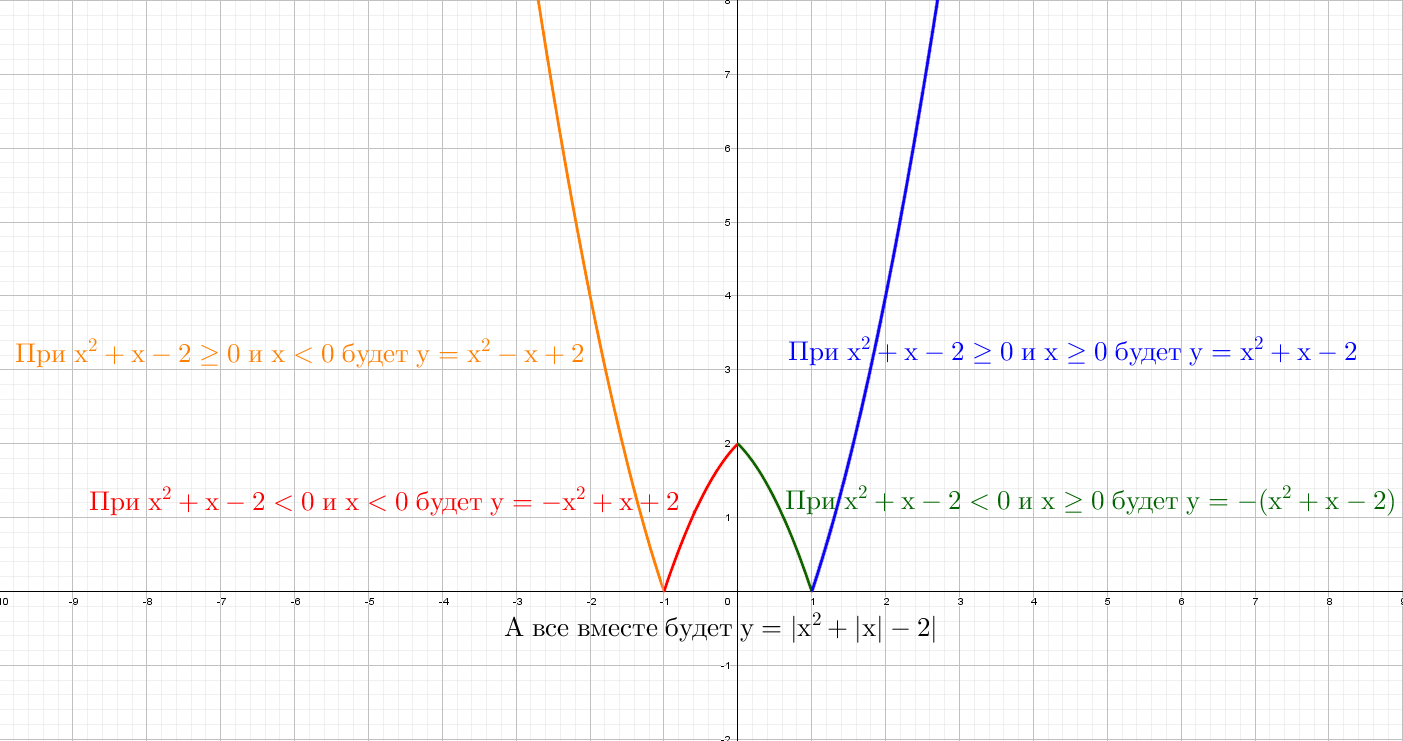
C двумя модулями кусочно-заданных графиков будет четыре:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль .
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Построение графиков с модулем
путём преобразований
Модуль аргумента и модуль функции
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.
Пример 1.
В этом примере оба графика получены из графика функции y = x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Пример 2.
В этом примере оба графика получены из графика функции y = x 2 − 2x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.
Ниже показаны примеры графиков различных функций, содержащих модуль, которые получены из графика функции \(y=\sqrt
- 1.
 2.
2. 3.
3. 4.
4. 5.
5.
| 1. \(y=\sqrt | 2. \(y=\sqrt<|x|>\) √|x| __ —> | 3. \(y=\sqrt<|x-1|>\) y = √|x − 1| _____ | 4. \(y=\sqrt<|x|-1>\) y = √|x| − 1 _____ | 5. \(y=|\sqrt |
IV Равенство вида |y| = f (x) по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции y = f(x) .
Для этого нужно:
- Построить график функции y = f(x) .
- Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
- Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.
Эти кривые также получены из графика функции \(y=\sqrt
- 6.
 7.
7. 8.
8.
| 6. \(|y|=\sqrt | 7. \(|y|=|\sqrt | 8. \(|y|=\sqrt<|x|>.\) |
Пример 3.
Задан график функции y = x 2 .
Построить кривые, удовлетворяющие уравнению, |y| = x 2 − 2|x| − 5 .
Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.
Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.
- 1.
 2.
2. 3.
3. 4.
4.
5.
 6.
6.
| 1.y = x 2 | 2.y = (x − 1) 2 | 3.y = (x − 1) 2 − 6 | 4.y = (|x| − 1) 2 − 6 |
| 5.y = (|x| − 1) 2 − 6, y ≥ 0 | 6.|y| = (|x| − 1) 2 − 6 |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Задан график функции y = x 2 .
Построить график функции y = |x 2 − 2x − 5| .
Сумма модулей
Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.
Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.
Пример 5.
Построить график функции y = |x + 2| + |x − 1| .
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1| , используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участках, например, при x = −3 и x = 3 . На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).
Теперь проверьте себя.
Пример 6.
Построить график функции y = |x + 2| + |x − 1| − |x| .
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Графики уравнений, содержащих знак модуля
Разделы: Математика
Цель:
- закрепить методы построения графика линейной функции,
- закрепить умение учащихся задавать уравнением функцию, заданную при помощи графика,
- познакомить учащихся с тем, каким образом влияет знак модуля на отображение графика линейной функции
При решении многих математических задач необходимо быстро и точно строить графики любых функций, изучаемых в школьном курсе алгебры. Т.к. на уроке предстоит много построений, начинаем, вспоминая, как строить график линейной функции y = kx + b на основе анализа углового коэффициента и коэффициента смещения (слайд 2)
Сопоставляем уравнения и графики (слайд 3):
Построим в тетрадях в одной системе координат графики функций (y = —x; y = —x -4; y = -1/3 x – 2; y = 2x + 5; y = x + 1), проверяя себя при помощи слайда 4
Вспомним определение модуля числа x (слайд 5)
Рассматриваем, как можно построить график функции y = |x| на основании определения модуля, отбрасывая части прямых, не лежащих в полуплоскостях x 0 (слайд 6)
Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)
Сравнивая графики и уравнения функций (слайд 8-9),
делаем вывод о том, как можно построить график функции y = |x + a| — b смещением графика функции y = |x| (слайд 10-11)
Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| — 2, y = |x+2| — 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12
Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:
При построении графиков очень важно научить ребят анализировать область определения и множество значений функции и “переносить” указанные множества на координатную плоскость.
Заполняем таблицу (слайд 12):
D(y) E (y) y = |x| y = |x – 3| y = |x – 3| +2 y = — |x| y = |x + 2| -5 y = — |x +2| -5
И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)
Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):
Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):
Анализируя графики и уравнения (слайд 18), ученики делают вывод о том, как влияет знак минуса перед модульными скобками на график. И самостоятельно задают уравнение по графикам, представленным на слайде 19.
Устно проговариваем уравнения функций по графикам (слайд 20):
Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:
Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:
http://mathematichka.ru/school/functions/Function_Graph_Modul.html
http://urok.1sept.ru/articles/512207