Построить лачх объекта поведение которого описывается дифференциальным уравнением

3. Частотные характеристики систем автоматического управления (АФЧХ, ЛАХ, ФЧХ) ч. 3.1

Лекции по курсу «Управление Техническими Системами» читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки» факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность!

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В этом разделе мы будем изучать частотные характеристики. Тема сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ

Будет интересно, познавательно и жестко.

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ

Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

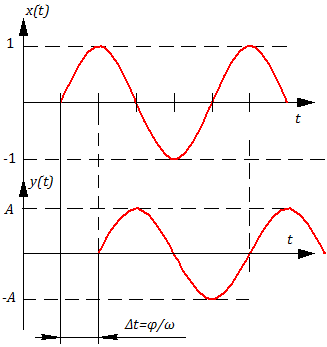
Формула синусоидального воздействия может быть записана как:

— сдвиг фазы (нередко называют — фаза);
— амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия x(t).

Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):

Определим связь между передаточной функцией и гармоничным воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий вид:

В показательной форме:

Запишем в показательной форме используя соотношения 3.1.1:

Подставим эти соотношения в (3.1.1) получим:

Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы зависят от частоты входного воздействия), то можно записать:

если вспомнить, что в преобразования Лапласа , то:

Получаем выражение для передаточной функции

— Амплитудно-фазовая частотная характеристика (АФЧХ)
Иногда называют частотной передаточной функцией.
Модуль АФЧХ= тождественно равен амплитуде выходного сигнала:

Сдвиг фазы выходного сигнала:

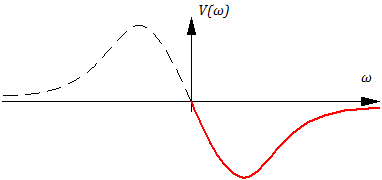
Обычно АФЧХ изображается на комплексной плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить в полярных координатах
Так же можно изображать в традиционных декартовых координатах:

Если использовать для представления W(s) форму W(s)=K·N(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К – общий коэффициент усиления звена (системы), то

Сдвиг фазы можно определить по виду многочленов и (см. формулу (3.1.9)) т.е. как разность фаз (аргументов) числителя и знаменателя:

Постоим АФЧХ для «абстрактного» звена (системы) с передаточной функцией:

Подставляя в формулу различные значения , получаем набор векторов, на комплексной плоскости

Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:

Амплитуда и сдвиг фазы рассчитываются для векторов, соответствующих положительным частотам и лежащих в 4 квадранте по формулам:

В общем случае для любых углов сдвига необходимо учитывать переход между квадрантами на плоскости. Тогда формула принимает вид:

где:
j = 0, 2, 3, 4. если вектор в I и IV квадрант;
j = 1, 3, 4, 4. если вектор в II и III квадранте.

Во всех технических системах отклик системы, как правило, отстает от входного воздействия, то есть сдвиг фазы всегда отрицательный. Исходя из формулы 3.1.10, степень полинома L(s) выше, чем полинома N(s). Поскольку обычно степень полинома L(s) выше, чем полинома N(s), то с увеличением частоты на входе в звено (в систему) сдвиг фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем вообще не получить выходного воздействия. Обычно при ω→ ∞ величина амплитуды на выходе звена стремится к 0, то есть lim A(ω→∞) = 0.

при замене на имеет зеркальное изображение.

Анализируя годографы АФЧХ при > 0 (сплошная линия на рисунке 3.1.3) и при Рисунок 3.1.4 – «Зеркальная» симметрия относительно оси ординат.

Кроме анализа свойств звена (системы) по годографу АФЧХ, широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).

ЛАХ определяется как Lm(ω)=20lgA(ω).

Поскольку зачастую удобнее использовать десятичные логарифмы (lg), чем натуральные(ln), в теории управления (также и в акустике) значительно чаще используется специальная единица – децибел (1/10 часть Бела):
+1Бел – единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) – соответствует увеличению в раз.

В формуле Lm(ω)=20lgA(ω) величина Lm(ω) измеряется также в децибелах. Происхождение множителя 20 таково: A(ω) – амплитуда, линейная величина, а мощность — квадратичная величина (например, напряжение в сети измеряется в Вольтах, а мощность () пропорциональна квадрату напряжения, поэтому в формуле для Lm(ω) стоит множитель 20 (чтобы привести ЛАХ (Lm(ω)) к традиционной мощностной характеристике).

Если больше на 20 дБ, то это означает, амплитуда больше амплитуды в 10 раз,

Окончательно: Lm(ω)=20lg│W(iω)│= 20lgA(ω)

Из этого следует, что +1 децибел (+1 дБ) соответствует увеличению амплитуды в раз (очень малая величина); -1 дБ – уменьшение амплитуды в раз.

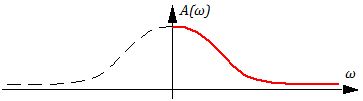
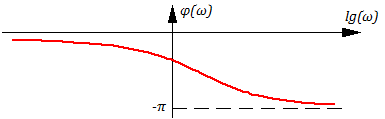
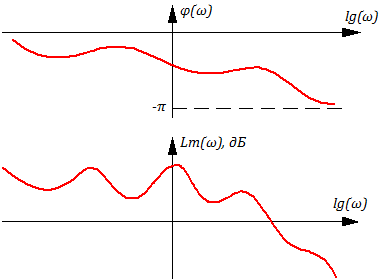
Графики A(ω) и φ(ω) имеют вид:

Учитывая, что “ω” обычно изменяется на порядки и значение A(ω) – также на порядки, график Lm(ω) строится, фактически, в логарифмических координатах, т.е. Lm(ω) =Lm(lg(ω)), например:

Наклон (– 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

Рассмотренные характеристики Lm(ω), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел “Устойчивость систем автоматического управления”).

Рисунок 3.1.10 – пример ЛАХ и ФЧХ для сложной системы

Пример 1

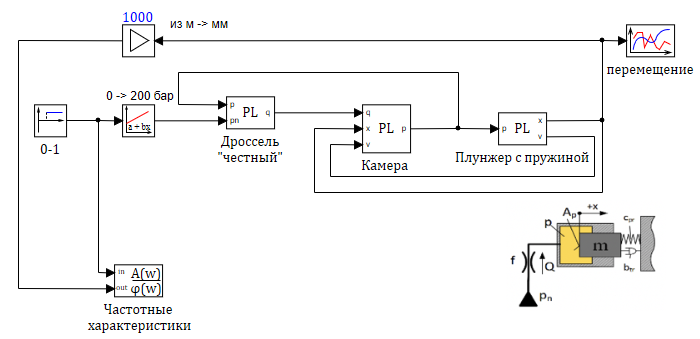
В качестве примера построим АФЧХ для демпфера, модель которого разобрана в этой статье. . Добавим на схему блок «Построение частотных характеристик», в качестве входа возьмем возмущающее воздействие, в качестве выхода — положение положение груза. Для наглядности иллюстрации примем в качестве выхода положение в миллиметрах (х1000), поскольку модель у нас размерная и результат получается в метрах уже достаточно маленьким примерно 0.004 метра. см. рис. 3.11

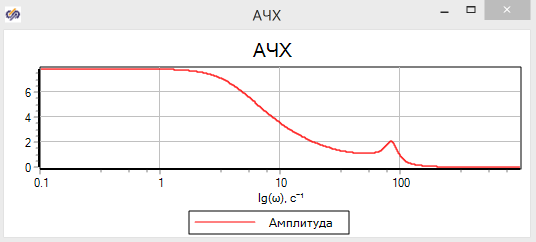
Параметры блока «Построение частотных характеристик» приведены на рисунке 3.1.12, для иллюстрации зависимости АЧХ и ЛАХ. Результат работы блока — график с выбранными параметрами — изображен на рисунке 3.1.13:

Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).

На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Пример 2

Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.

Для начала посмотрим на модель в виде блоков.

Модель, подготовленная для анализа, представлена на рисунке 3.1.15. В отличие от исходной модели, описанной ранее, входное воздействие задается блоком «ступенька» с скачком с 0 до 1 на 10 секунде расчёта. В блоке «линейная функция» происходит пересчет сигнала «ступенька»:
0 — соответствует 200 бар в камере (конечное состояние в предыдущем примере)
1 — соответствует 400 бар в камере.
Это сделано для того, чтобы можно было подавать синусоидальный сигнал и не получать отрицательное давление в камере плунжера. Также для наглядности графика мы усиливаем выходное перемещение, переводя его из метров в миллиметры.

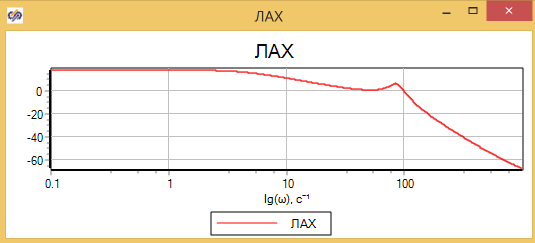
Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)

Блок «Построение частотных характеристик» осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.

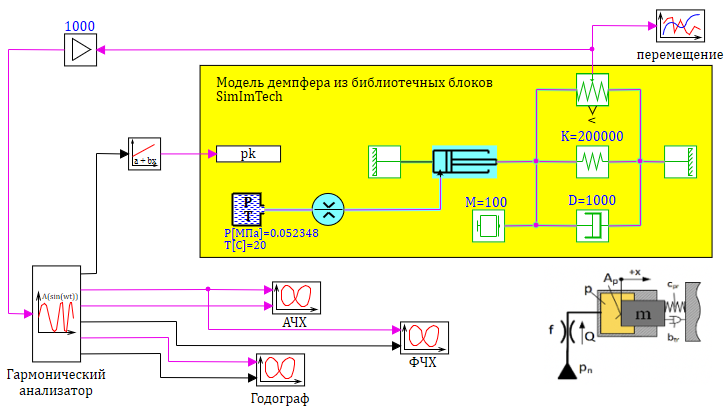
Для подробных и нелинейных моделей, блок «Построение частотных характеристик» может не работать из за наличия разрывов и нелинейностей в модели. Как например, для «точной» модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок «Гармонический анализатор», который подключается ко входу модели и генерирует синусоидальное воздействие. В этот же блок направляется отклик системы, и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока «фазовый портрет».

Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7

Расчеты с моделью показывают, что при сохранении общего вида графиков значения, полученные для «подробной модели», отличаются от линеаризованной модели (см. рис. 3.18 — 3.19)

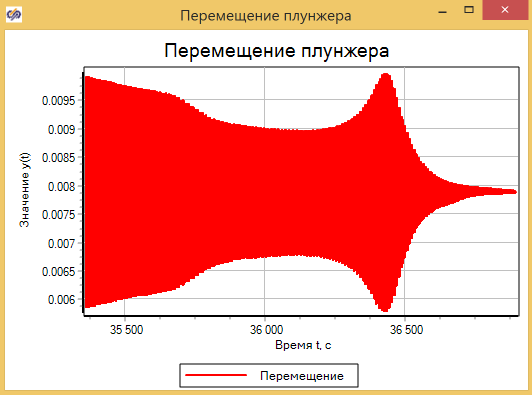
Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

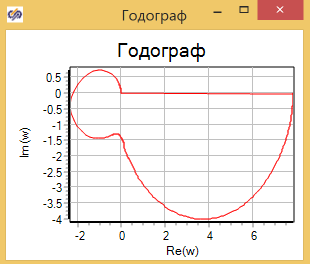
Блок «Гармонический анализатор» имеет выходы:
Re(w*t) – текущее значение действительной части амплитудно-фазовой частотной характеристики исследуемой системы;
Im(w*t) – текущее значение мнимой части амплитудно-фазовой частотной характеристики.
Это позволяет построить годограф исследуемой системы с помощью фазового портрета. (см. рис. 3.1.21)

Модели, использованные для иллюстрации в лекции можно взять здесь…

Как построить лачх по передаточной функции

Методика построения лачх

1. Определяются сопрягающие частоты:

. (4.1)

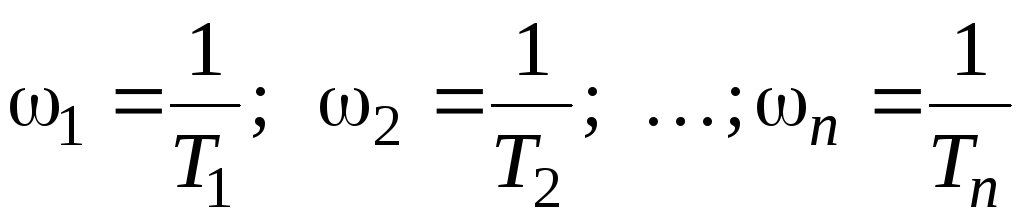
Полученные значения откладываются на оси частот в логарифмическом масштабе (,, …,).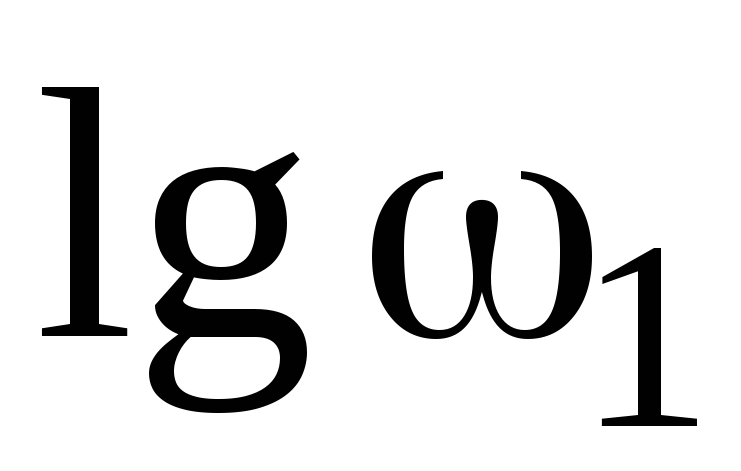

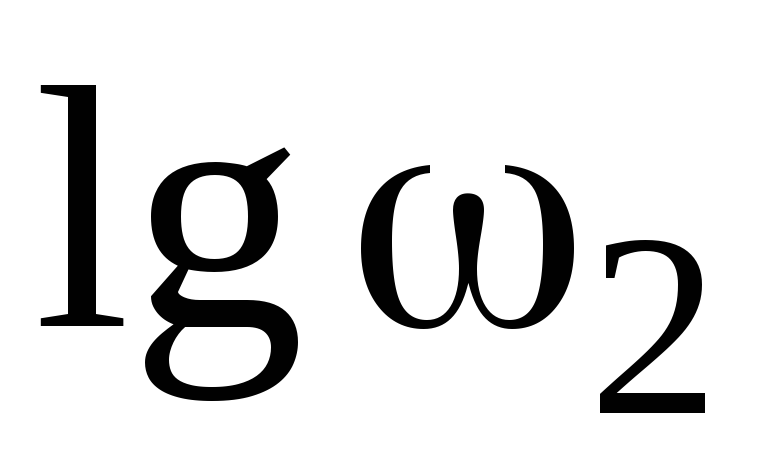
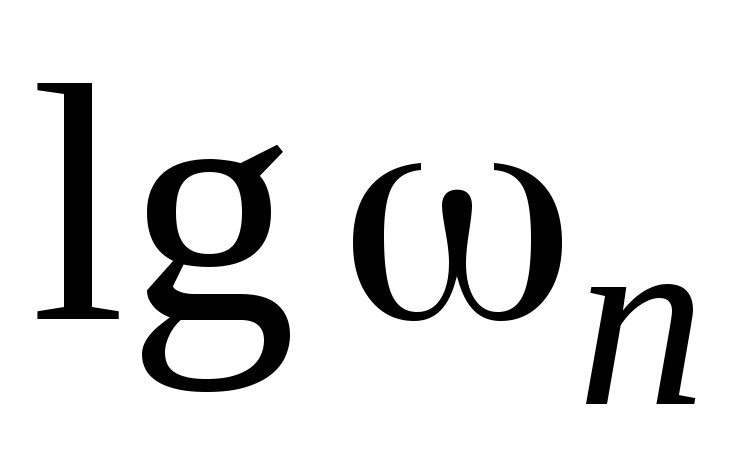
2. На начальном интервале частот 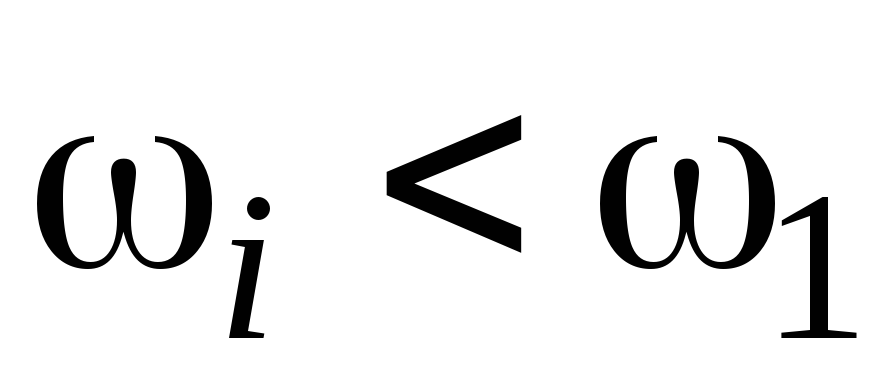наклон ЛАЧХ зависит от вида системы:

если система статическая, то в интервале частот 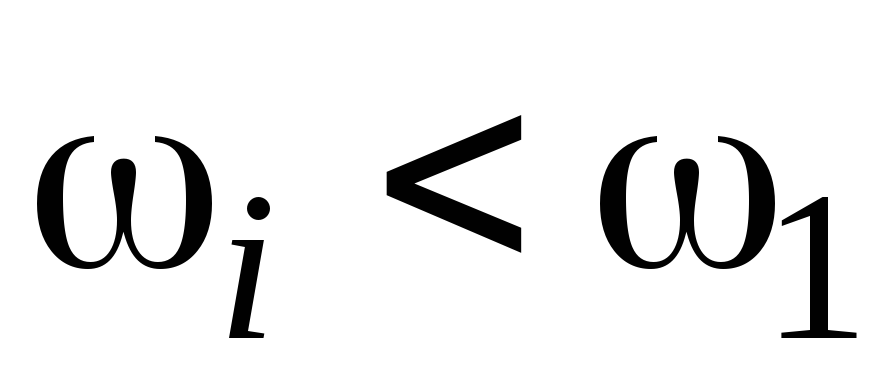откладывается горизонтальная прямая проходящая на расстоянии 20lgk дБ от логарифмической оси частот;

если система астатическая (полином в знаменателе передаточной функции W(p) имеет нулевые корни), то в интервале частот 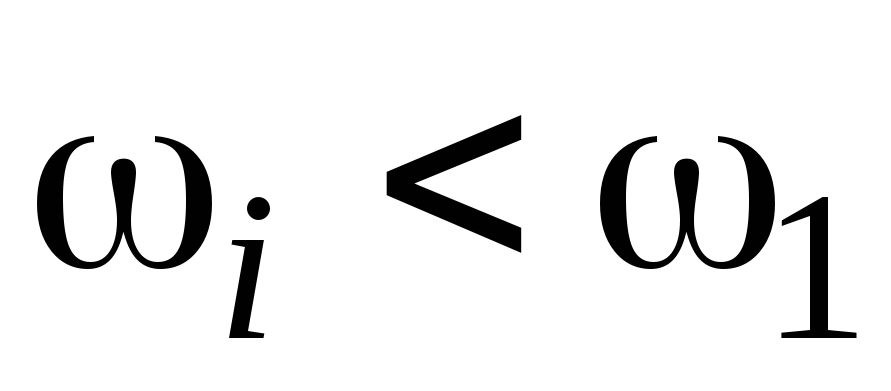проводится прямая с отрицательным наклоном –20v дБ/дек, где v – степень астатизма системы (число нулевых корней знаменателя передаточной функции), через точку с координатами (lg1, 20lgk), т.е. (0, 20lgk);

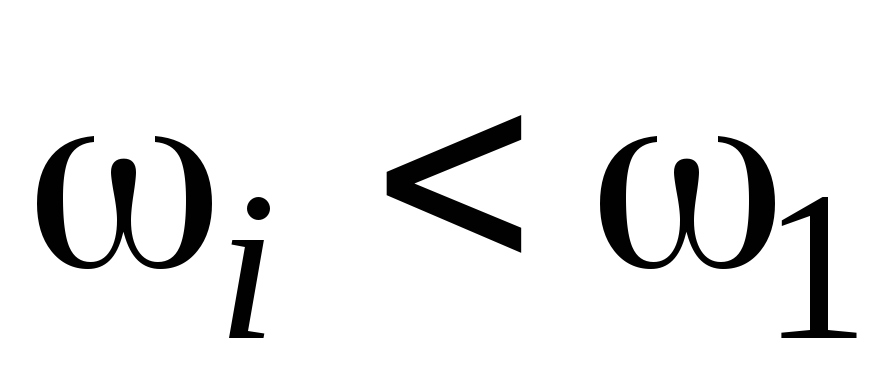
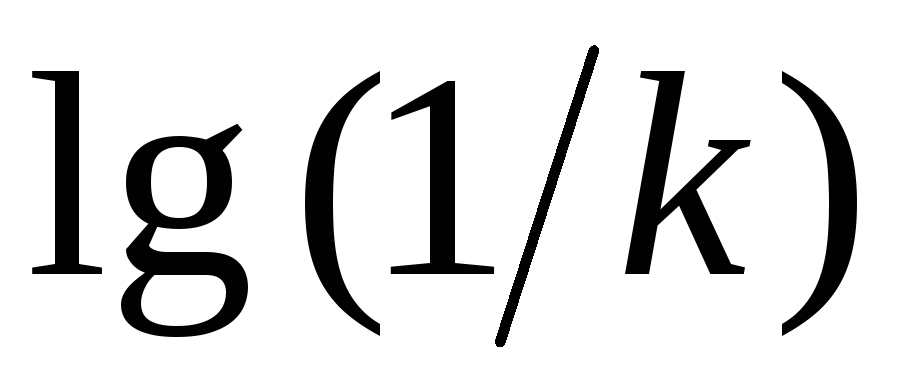
если система с нулевыми нулями (полином в числителе передаточной функции W(p) имеет нулевые корни), то в интервале частот проводится прямая с положительным наклоном +20λ деб/дек, где λ – число нулевых корней числителя передаточной функции, через точку с координатами (, 0).

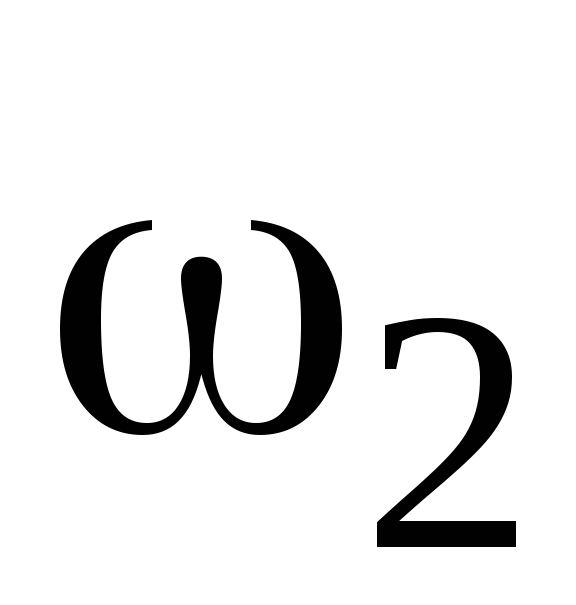
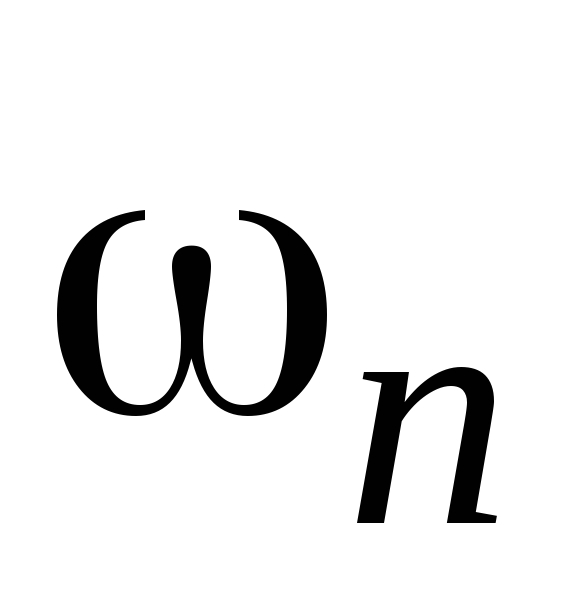
3. После каждой сопрягающей частоты , …, наклон ЛАЧХ L(ω) меняется в зависимости от того, какому звену принадлежит сопрягающая частота. В итоге получается асимптотическая ЛАЧХ в виде ломаной прямой.

4. При необходимости более точного построения точки ЛАЧХ в окрестностях точек излома корректируются значения L(ω) с использованием специальных таблиц поправок, приведённых в 4.

Примечание: ЛФЧХ строится так же, как и ЧХ, но при этом используется логарифмический масштаб частот.

Пример построения лачх статической сар

Дана передаточная функция статической системы:

, (4.2)

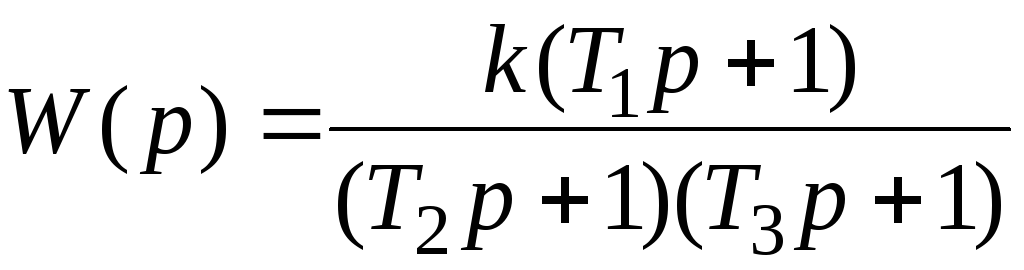
Построить асимптотическую ЛАЧХ для статической системы.

Для построения ЛАЧХ воспользуемся формой представления комплексного числа в соответствии с формулой Эйлера:

, (4.3)

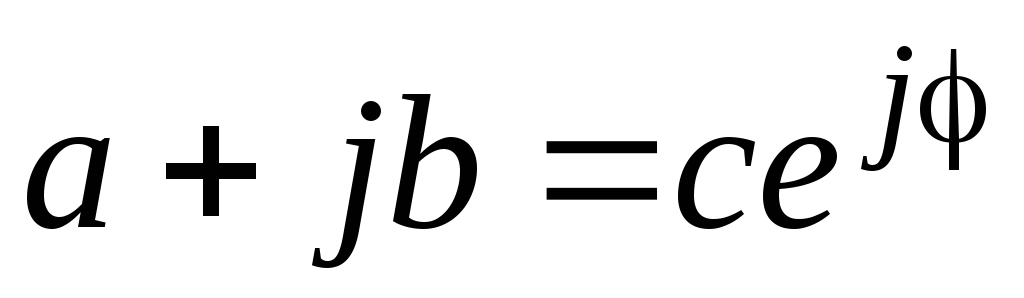
где ; .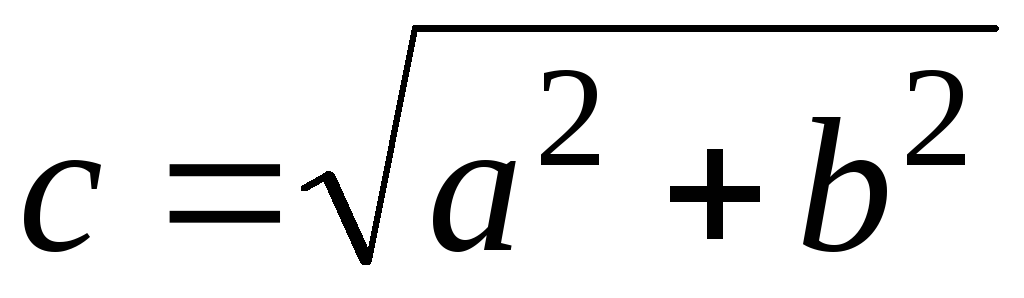

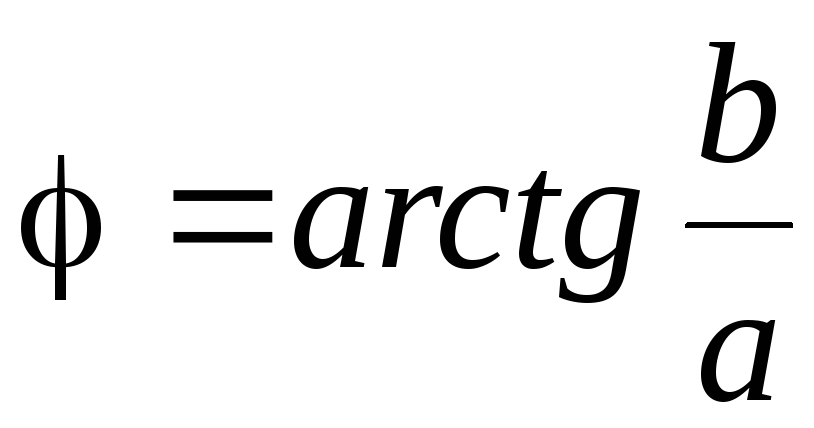
Найдём частотную передаточную функцию:

(4.4)

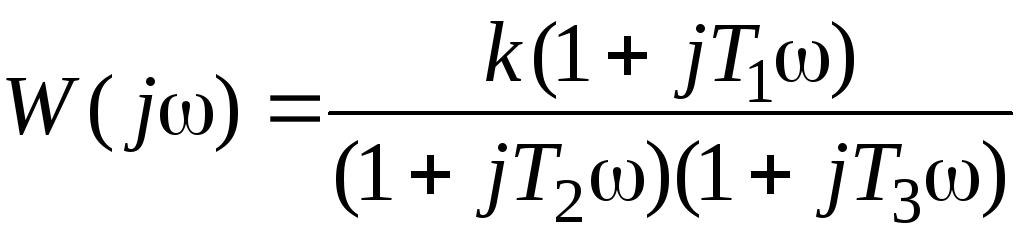
или с учётом (4.3)

. (4.5)

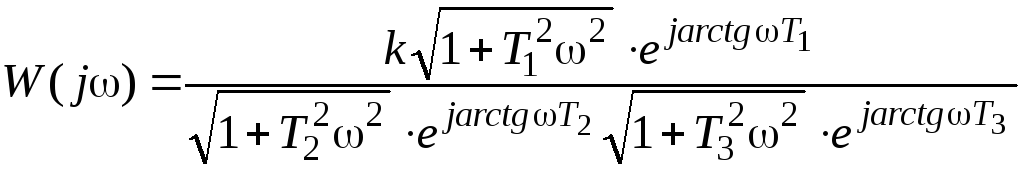
Тогда модуль частотной передаточной функции

. (4.6)

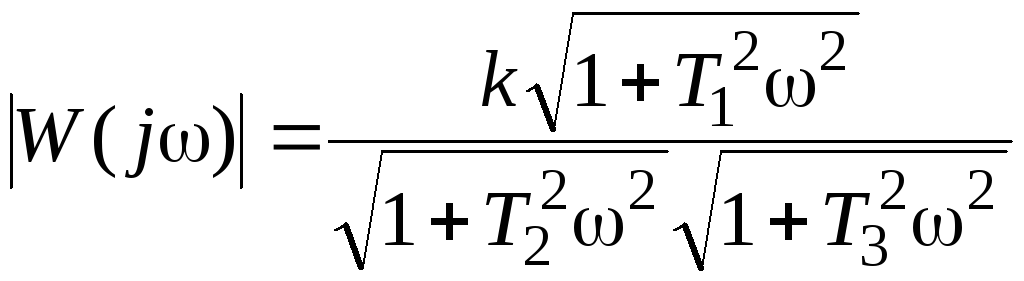
Отсюда имеем, что

. (4.7)

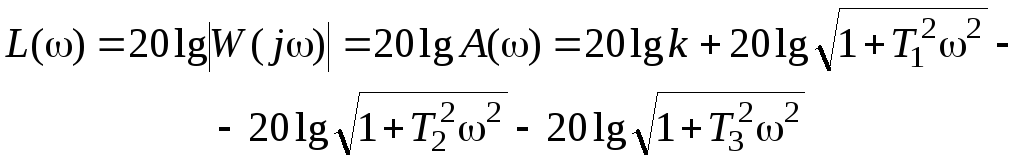
Определим сопрягающие частоты:

, ;

, ;

, .

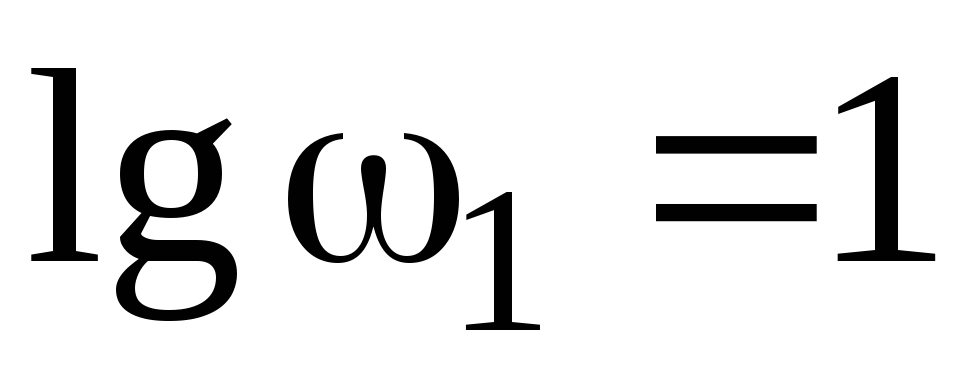
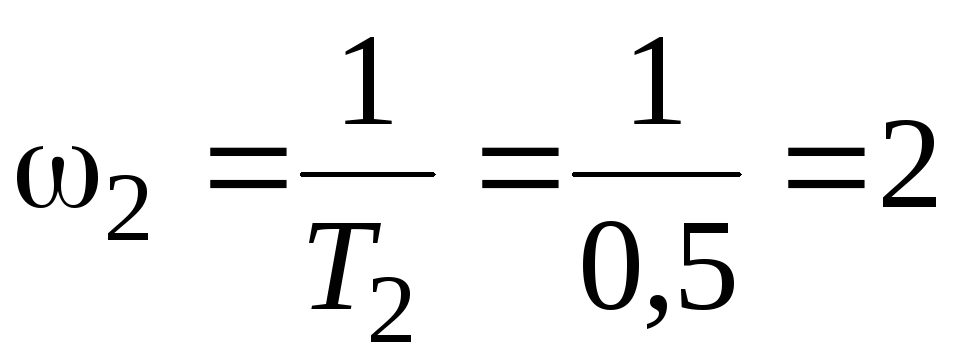
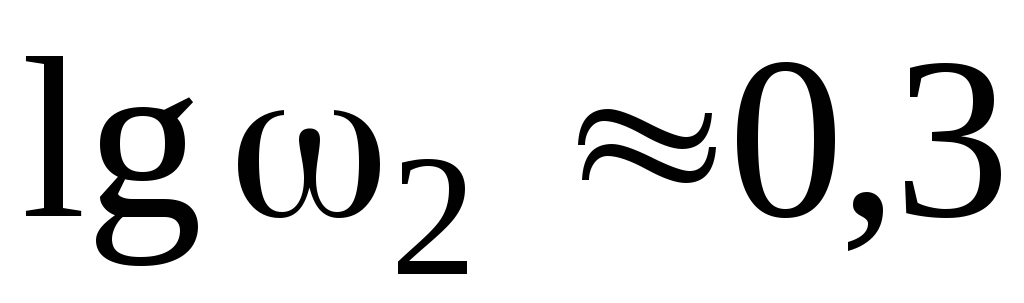
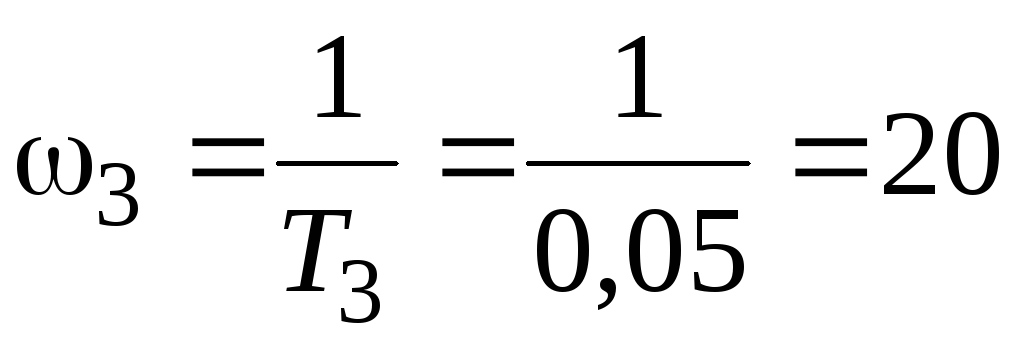
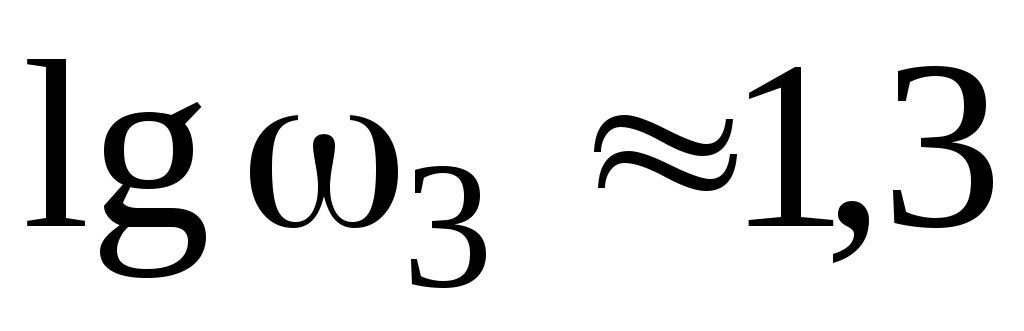
Отложим значения частот на оси частот в логарифмическом масштабе, как показано на рисунке 4.1.

Рисунок 4.1 – Пример ЛАЧХ статической САУ

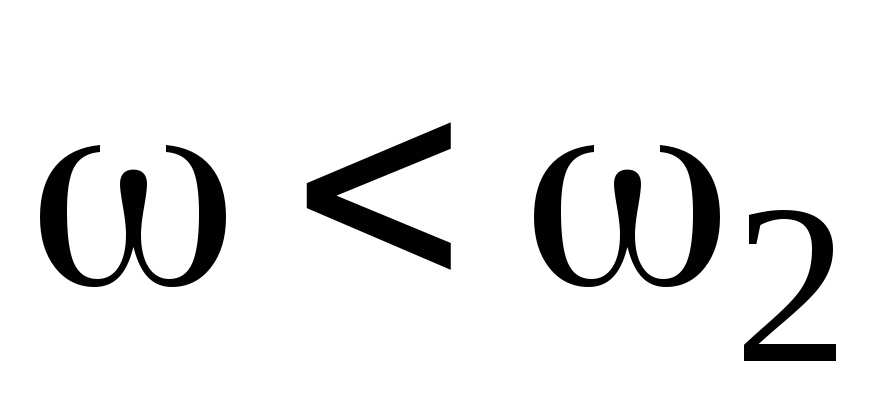
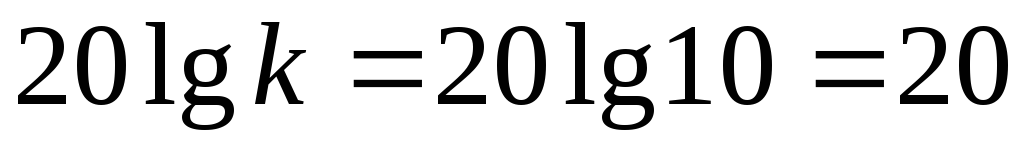
Так как система статическая, то в интервале частот проводится горизонтальная прямая на расстоянии 20lgk дБ от логарифмической оси частот

дБ (4.8)

до пересечения с ординатой, проходящей через частоту ω₂ (точка А).

Так как частота ω₂ принадлежит звену с отрицательным наклоном, то из точки А проводится прямая с наклоном –20дБ/дек до пересечения с ординатой через частоту ω₁ (точка В). Наклон –20дБ/дек получается при соединении точек с координатами (0, 20lgk) и (1,0) на рисунке 4.1 линия 1.

Частота ω₁ принадлежит звену с положительным наклоном 20дБ/дек, поэтому в интервале частот от ω₁ до ω₃ получим горизонтальную прямую (отрезок ВС).

Частота ω₃ принадлежит звену с отрицательным наклоном –20дБ/дек, поэтому L(ω) дальше пойдёт под наклоном 20дБ/дек из точки С.

Пример построения лачх астатической сар

Дана передаточная функция астатической системы:

, (4.9)

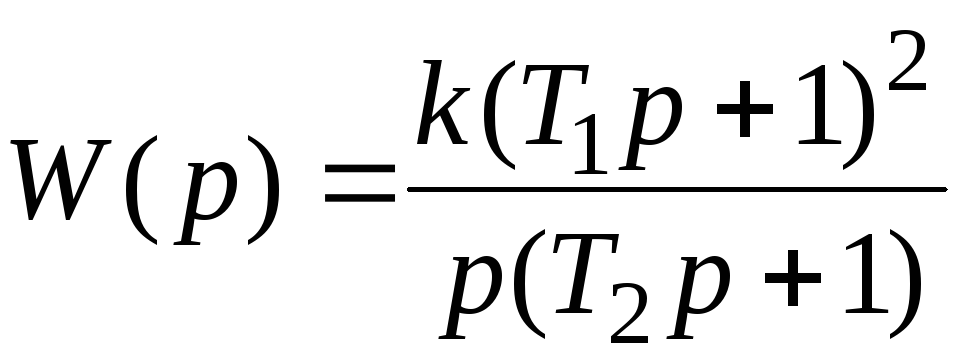
Построить ЛАЧХ для астатической системы первого порядка.

Примечание: Формально степень астатизма САР определяется степенью переменной р в знаменателе передаточной функции. Так как в примере р в первой степени, значит рассматриваемая САР имеет астатизм первого порядка.

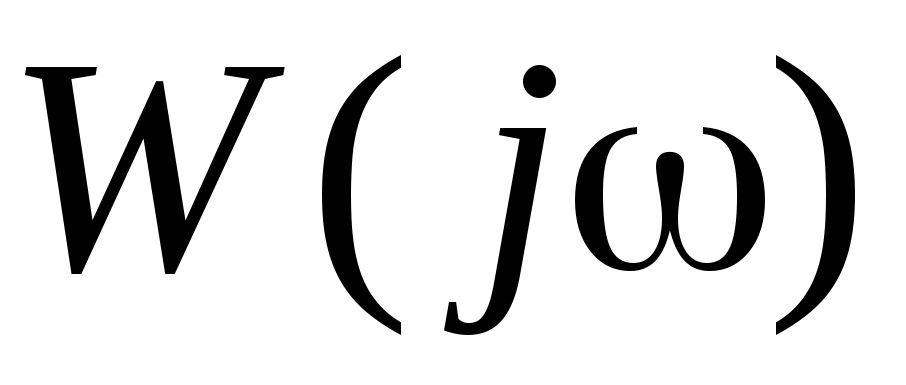
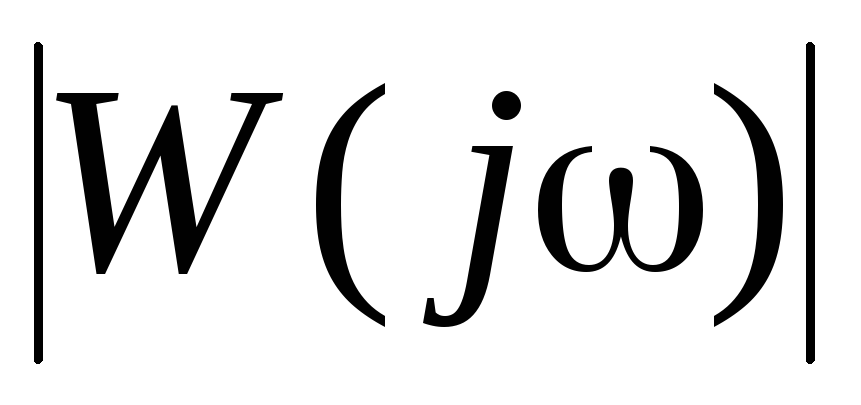
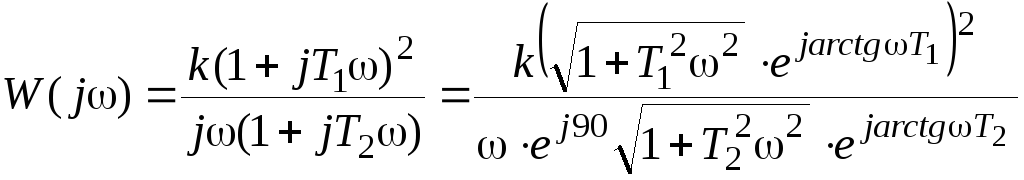
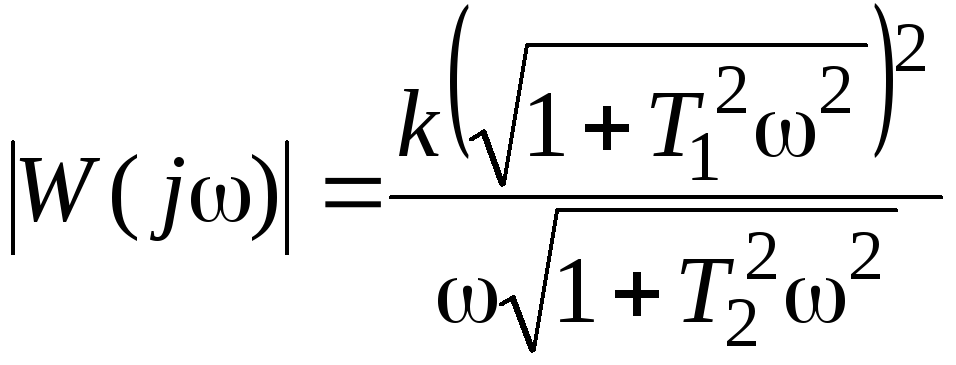
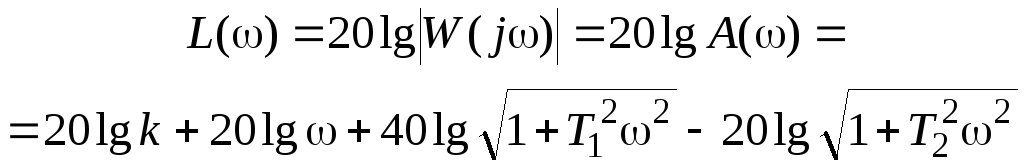
Аналогично предыдущему примеру найдём и .

. (4.10)

. (4.11)

. (4.12)

Определим сопрягающие частоты:

, ;

, .

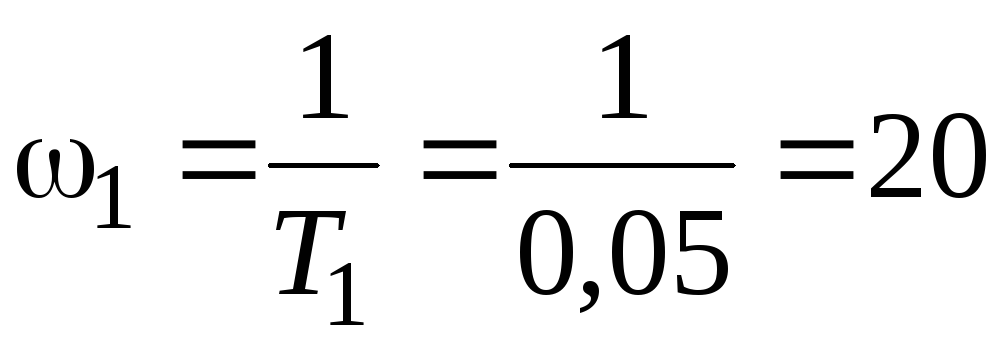
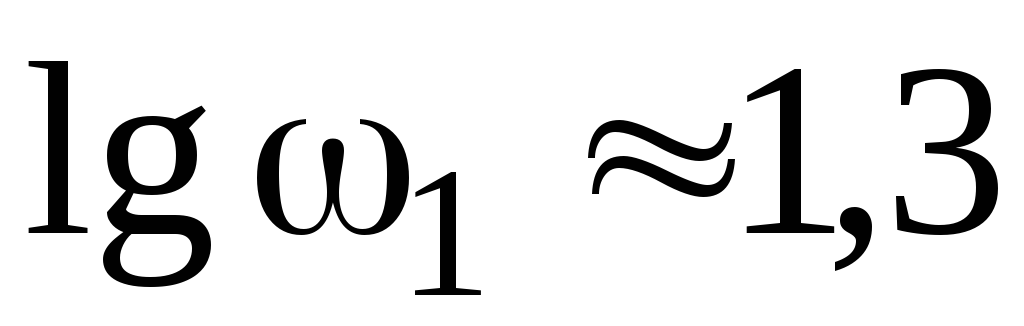
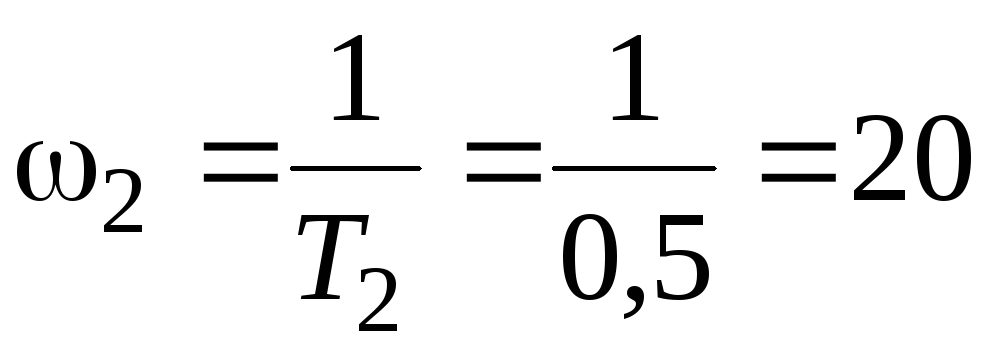
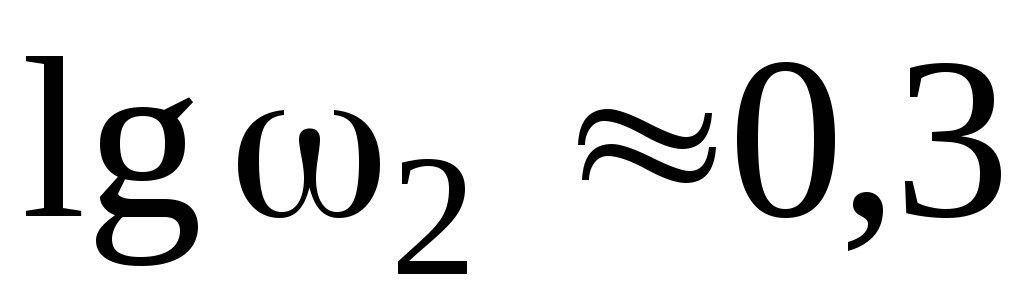
Отложим их на оси частот в логарифмическом масштабе, как показано на рисунке 4.2.

Рисунок 4.2 – Пример ЛАЧХ для астатической САР

На участке частот 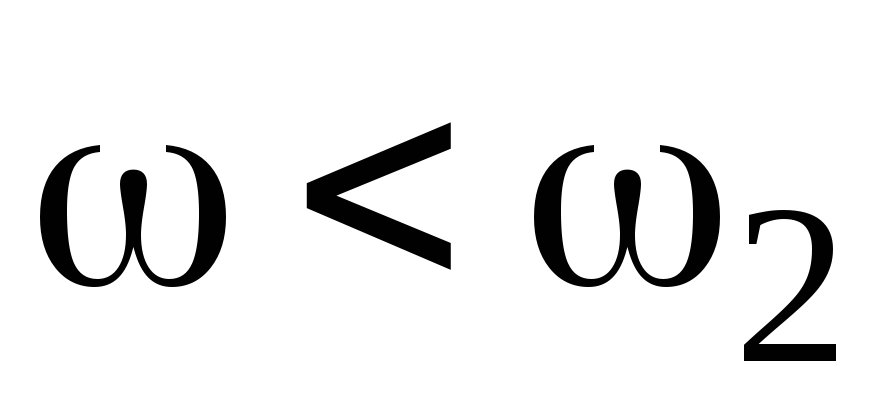проводим прямую с наклоном –20дБ/дек через точку с координатами (0; 20lgk). Масштаб наклона – 20деб/дек показан линией 1, так как 20lgk=20lgω, а значит lgω= lgk= lg10=1.

На участке частот (ω1;ω2) проводится прямая с наклоном –40 деб/дек, так как звено с частотой имеет отрицательный наклон –20 деб/дек. Масштаб наклона – 40деб/дек показан линией 2.

На участке частот (ω2;∞) L(ω) имеет наклон –20деб/дек, так как звено с частотой ω2 имеет положительный наклон +20деб/дек.

ЗАДАНИЕ

На курсовое проектирование по дисциплине

«Основы теории управления»

Студенту Макееву Александру Александровичу , группа 434

(фамилия, имя, отчество)

Направление подготовки 230100 – Информатика и вычислительная техника

Специальность 230104 – Системы автоматизированного проектирования

ТемаРазработка программы для синтеза САУ методом ЛАЧХ

Исходные данные к проекту:

Список используемых источников:

1 Теория автоматического управления : учеб. для вузов. В 2 ч. – Ч.1: Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов [ и др. ] ; под ред. А. А. Воронова. – М. : Высш. шк. , 1986. – 367 с.

2 Макарова, Л. Ф. Основы теории управления: конспект лекций / Л. Ф. Макарова. – СПб.: СПбГТИ(ТУ). – 2015.

3 Портал Python 2.7.4 Documentation [Электронный ресурс]: Электронные данные – Режим доступа: https://docs.python.org

4 Портал Welome to Kivy [Электронный ресурс]: Электронные данные – Режим доступа: http://kivy.org/docs

5 Портал Stack Overflow [Электронный ресурс]: Электронные данные – Режим доступа: http://stackoverflow.com

Требования к аппаратному программному обеспечению

Intel Core i5 3230-M 2.6 GHz, ОЗУ 6 Гб.

ОС Linux Ubuntu Mate 14.04; текстовой редактор – Sublime Text 3, средства оформления документации — Microsoft Office Word 2007.

Дата выдачи задания 17.09.2015

Дата представления курсового проекта к защите25.12.2015

Руководитель Л.Ф. Макарова

(подпись, дата) (инициалы, фамилия)

Зав. кафедрой Т.Б. Чистякова

(подпись, дата) (инициалы, фамилия)

Задание принял(а) к выполнению студент(ка)

Цель и задачи курсового проекта 4

1 Аналитическая часть 6

1.1 Построение ЛАЧХ_ 6

1.2 Построение желаемой ЛАЧХ_ 7

1.3 Построение ЛФЧХ_ 8

1.4 Анализ устойчивости_ 8

2 Практическая часть 10

2.1 Анализ передаточной функции заданного соединения звеньев_ 10

2.2 Построение ЛАЧХ_ 11

2.3 Построение ЛФЧХ_ 12

2.4 Блок-схема алгоритма_ 14

2.5 Основные дисплейные фрагменты_ 15

Список используемых источников 18

ПРИЛОЖЕНИЕ А_ 19

ПРИЛОЖЕНИЕ Б_ 20

ПРИЛОЖЕНИЕ В_ 25

Цель и задачи курсового проекта

Цель курсового проекта:

Для системы с заданной передаточной функцией разработать программу для построения асимптотической логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ).

В процессе проектирования необходимо решить следующие задачи:

— провести анализ передаточных функций и логарифмических частотных характеристик типовых динамических звеньев;

— разработать алгоритм и программу построения ЛАЧХ и ЛФЧХ соединения типовых звеньев;

— разработать подпрограмму графического определения запасов устойчивости по модулю и фазе с помощью ЛАЧХ и ЛФЧХ;

— провести тестирование разработанной программы, состоящее в изменении параметров заданной передаточной функции с целью увеличения запасов устойчивости или улучшения качества функционирования системы в смысле повышения ее быстродействия.

Введение

В практической автоматике при расчетах АСР удобно использовать частотные характеристики, построенные в логарифмической системе координат (ЛЧХ). Применение логарифмического масштаба позволяет наглядно отображать частотные характеристики в большом диапазоне частот, представлять ЧХ отрезками ломаных линий и определять характеристики сложных систем простым суммированием или вычитанием ЛЧХ, входящих в эти системы элементов.

ЛЧХ являются исчерпывающими характеристиками системы, по которым можно восстановить ее ПФ и определить параметры.

Главное достоинство ЛАЧХ – возможность построения их во многих случаях практически без вычислений. Это проявляется в тех случаях, когда представляется в виде произведения сомножителей. Тогда результирующая ЛАЧХ находится суммированием ординат ЛАЧХ, соответствующих отдельным сомножителям.

Аналитическая часть

В теории автоматического управления широко используются логарифмические амплитудно-частотные и фазо-частотные характеристики (ЛАЧХ и ЛФЧХ). Они получаются путем логарифмирования коэффициента передаточной функции (КПФ):

ЛАЧХ получают из первого слагаемого, которое умножается на 20:

Величина откладывается по оси ординат в децибелах или белах (1 Б = 10 дБ).

Бел – единица измерения отношения мощности двух сигналов. Если мощности двух сигналов отличаются в 10 раз, то это отличие соответствует 1 Б ( ). Два сигнала отличаются на 1 дБ, если , что соответствует .

По оси абсцисс откладывается частота в логарифмическом масштабе, которая измеряется в декадах.

Декада – интервал частот, заключенный между произвольным значением и его десятикратным значением. Отрезок, соответствующий одной декаде равен 1. Логарифмическая шкала не имеет нуля и не может пересекаться вертикальной осью в любом месте.

ЛФЧХ, получаемая из второго слагаемого, отличается от ЛАЧХ только масштабом по оси абсцисс. Величина откладывается по оси ординат в градусах или радианах (для элементарных звеньев она не выходит за пределы ). Таким образом, при построении ЛФЧХ логарифмический масштаб применяется только для оси абсцисс.

Построение ЛАЧХ

При построении ЛАЧХ по оси ординат наносится равномерный масштаб, желательно кратный 20 дБ. Начало координат помещают в точке = 1. Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля . Точка лежит на оси частот слева в бесконечности, т.к. . В зависимости от интересующего диапазона частот ось ординат можно проводить и через другую точку так, чтобы можно было показать весь ход ЛАЧХ.

Для каждой из сопрягающих частот определяется наклон характеристики по сравнению с тем наклоном, который эта характеристика имела до сопрягающей частоты в соответствии с видом звена, представленных в таблице 1.

Таблица 1 – Наклоны ЛАЧХ типовых динамических звеньев

Вид звена	Передаточная функция	Наклон (дБ/дек)
Усилительное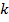
Апериодическое		-20
Колебательное		-40
Инерционное II-го порядка		-40
Дифференцирующее		+20
Форсирующее I-го порядка		+20
Форсирующее II-го порядка		+40

Построение желаемой ЛАЧХ

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые или требуемые статические и динамические свойства. Желаемая ЛАЧХ состоит из 3-х основных асимптот:

-низкочастотной ( )

-среднечастотной ( )

-высокочастотной ( )

Низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические свойства САУ (точность) и ее наклон зависит от порядка астатизма системы : при наклон ЛАХ равен -20 дБ/дек, при наклон ЛАХ равен -40 дБ/дек. Если передаточная функция имеет передаточный коэффициента и порядок астатизма , удовлетворяющие требованиям, то низкочастотной асимптотой желаемой ЛАЧХ является низкочастотная асимптота ЛАЧХ неизменяемой части системы. Если наклон низкочастотной асимптоты равен 0 или -20 дБ/дек, то наклон сопрягающей асимптоты выбирается равным -40 или -60 дБ/дек.

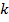
Среднечастотная асимптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяет динамические свойства системы (устойчивость и показатели переходной характеристики). Построение начинают с выбора частоты среза , которая определяет зависимость перерегулирования и времени регулирования от максимума ВЧХ замкнутой системы, причем дано в виде функции . Среднечастотная асимптота проводится через точку с наклоном -20 дБ/дек влево и вправо от до получения определенных запасов устойчивости и допустимое перерегулирование. Протяженность устанавливается исходя из необходимого запаса устойчивости. Из этих соображений выбирают ее сопряжение с низкочастотной асимптотой. Кроме того, сопрягающую асимптоту следует выбрать так, чтобы характеристика возможно меньше отличалась от ) для того, чтобы при вычитании получалось в реализации наиболее простое КУ.

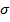
Высокочастотная асимптота мало влияет на свойства системы, поэтому ее следует выбирать так, чтобы корректирующее устройство (КУ) было возможно более простым. Это достигается при совмещении высокочастотных асимптота характеристик и . Если совмещение не удается, то высокочастотная асимптота должна иметь тот же наклон, что и высокочастотная асимптота .

Построение ЛФЧХ

Довольно часто ЛАЧХ и ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах системы.

Для построения ЛФЧХ используется также ось частот (ось абсцисс). По оси ординат откладывается фаза в градусах (или радианах) в линейном масштабе. Положительный сдвиг по фазе откладывается по оси ординат вверх, а отрицательный – вниз.

Анализ устойчивости

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой системы. Применение метода ЛЧХ дает возможность увидеть влияние того или иного параметра системы на ее устойчивость и переходный процесс, а также позволяет сравнительно определить характеристику КУ, обеспечивающего требуемые показатели качества системы.

САУ, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если ордината ЛФЧХ на частоте среза системы по абсолютной величине меньше, чем , т.е. если .

Для того чтобы замкнутая система была устойчива необходимо и достаточно, чтобы на всех частотах, где ЛАЧХ разомкнутой системы положительная ( ), фазовый сдвиг не достигал или достигал его четное число раз.

Замкнутая система будет находиться на границе устойчивости, если на той же частоте среза , где ЛАЧХ разомкнутой системы обращается в 0 ( ), значение ФЧХ равно . Это соответствует состоянию разомкнутой системы, когда ее АФЧХ проходит через точку , т.е. когда модуль . Так как , то система будет находиться на граице устойчивости, если на частоте .

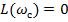
Запас устойчивости по модулю показывает, во сколько раз можно увеличить коэффициента усиления системы без потери устойчивости. Определяется на частоте, где ФЧХ дотигает значения .

Запас устойчивости по фазе определяется на частоте , где и характеризует отклонение от , т.е. .

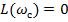
Эмпирическим путем установлено, что для нормальной работы многих систем управления необходимо обеспечивать следующие запасы устойчивости: , .

Для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы частота, при которой ЛФЧХ пересекает линию , была больше частоты среза.

Практическая часть

Рассмотрим пример системы с передаточной функцией (ПФ):

Обычно объект управления представляет собой последовательную цепочку типовых звеньев, поэтому L₀(со) можно получить, суммируя отдельные ЛЛЧХ, причем в этом случае удобнее строить асимптотические характеристики звеньев. Подобное суммирование позволяет предложить следующую процедуру построения L₀(co).

Пример 6.5. Построить асимптотическую ЛАЧХ объекта, передаточная функция которого имеет вид

где коэффициент усиления k_u = 10, а постоянные времени Г, = 10 с, Т₂ = 1 с. Решение

Используем предложенную процедуру для построения ЛАЧХ объекта. Предварительно определим характерные точки:

и отметим их па осях координат (рис. 6.10).

Рис. 6.10. Асимптотическая ЛАЧХ объекта для примера 6.5

Построение ЛАЧХ начинается из области низких частот, которая расположена левее первой частоты сопряжения. Низкочастотная асимптота имеет наклон -20 дБ/дек., так как передаточная функция объекта содержит интегрирующее звено. Проводится она до частоты lgco, так, чтобы ее продолжение пересекало ось ординат в точке 20lg&₀.

Па частоте lgco, происходит излом характеристики на -20 дБ/дек., что соответствует апериодическому звену в составе W₀(p). До следующей частоты сопряжения (lgco₂) наклон асимптоты будет равен -40 дБ/дек.

Излом характеристики на частоте lgco₂ равен -20 дБ/дек., так как в составе W₀(p) есть апериодическое звено с постоянной времени Т₂. Следовательно, наклон последней асимптоты ЛАЧХ объекта будет равен -60 дБ/дек.

Для построения ЛАЧХ объекта с произвольной передаточной функцией

следует, заменив в ней р на jсо, перейти к выражению для частотной характеристики

Амплитудная частотная характеристика определяется как

что позволяет определить 1₀(со) в виде

Таким образом, логарифмическая амплитудная частотная характеристика объекта находится как разность логарифмических характеристик его числителя и знаменателя.

Логарифмические частотные характеристики

Министерство образования Российской Федерации

Балтийский государственный технический университет “Военмех”

Кафедра систем обработки информации и управления

В. Ю. ЕМЕЛЬЯНОВ

Конспект лекций

Санкт-Петербург

Логарифмическая амплитудно-частотная характеристика (логарифмическая амплитудная характеристика, ЛАХ) L ( w ) определяется путем преобразования амплитудно-частотной характеристики (АЧХ) A ( w ):

Для логарифмической фазо-частотной характеристики (ЛФЧХ, ЛФХ) используется выражение j ( w ), полученное для обычной фазо-частотной характеристики (ФЧХ).

Очевидно, ЛАХ и ЛФЧХ не содержат новой информации по сравнению с АЧХ и ФЧХ. Целесообразность их получения и использования полностью определяется особыми правилами их построения, предоставляющими широкие возможности для построения удобных и наглядных процедур анализа и синтеза систем управления. Аппарат ЛАХ и ЛФЧХ является основой классической теории линейных непрерывных и дискретных систем.

Необходимо отчетливо представлять себе необходимость точного соблюдения правил построения ЛАХ и ЛФЧХ, так как без этого рассматриваемые характеристики теряют смысл, и их применение с нарушением правил построения приводит к неверным результатам.

При построении рассматриваемых характеристик для горизонтальной оси (оси частот) используется логарифмический масштаб (рис.1), то есть положение конкретных частот на оси соответствует значениям их десятичных логарифмов. Другими словами, в обычном линейном масштабе по горизонтальной оси откладываются не сами частоты w , а значения lg w . Угловая частота, как и обычно, измеряется в 1/с (рад/с), но в силу применяемого масштаба единицей измерения по оси абсцисс является декада (определение приводится ниже).

На рис.1 выше горизонтальной оси указаны значения частот, ниже оси – их десятичных логарифмов.

Отметим следующие обстоятельства, характерные для используемого логарифмического масштаба:

1. Отрицательные частоты не рассматриваются.

2. Отметка частоты w = 0 на оси отсутствует. При w ® 0 lg w ® — ¥ , и соответствующие отметки частоты смещаются по горизонтальной оси влево в бесконечность.

3. Вертикальная ось проводится через отметку частоты, соответствующую нижней границе диапазона существенных частот для изображаемых характеристик.

4. Изменению значения частоты в k раз соответствует отрезок оси постоянной длины независимо от его расположения на оси (то есть абсолютных значений частот).

5. Отрезок горизонтальной оси, соответствующий десятикратному изменению частоты, называется декадой. Длина декады, очевидно, постоянна независимо от ее расположения на оси.

6. В дальнейшем изложении по оси абсцисс откладываются и указываются только значения частоты в логарифмическом масштабе.

На вертикальной оси откладываются в линейном масштабе значения L ( w ) в децибелах. С горизонтальной осью совмещается отметка 0 дБ.

Логарифмическая фазо-частотная характеристика строится совместно с ЛАХ, причем горизонтальная ось у обеих характеристик полностью совпадает, а вертикальная ось для ЛФЧХ совмещается с вертикальной осью ЛАХ следующим образом:

1. Направление положительного отсчета значений ЛФЧХ – вниз.

2. С отметкой 0 дБ для ЛАХ (пересечение с горизонтальной осью) совмещается отметка -180 ° для ЛФЧХ (рис.1).

Рассмотрим некоторые примеры построения логарифмических характеристик, позволяющие обнаружить основные закономерности их формирования.

1. Безынерционное звено:

Характеристики показаны на рис. 2.

,

,

Поскольку вдоль горизонтальной оси используется линейный масштаб для l g w , график L ( w ) будет представлять собой прямую линию (рис. 3). Ее наклон принято измерять в децибелах на декаду (дБ/дек). В рассматриваемом примере при увеличении w в 10 раз, то есть на одну декаду, L ( w ) получит приращение

дБ.

Поэтому наклон ЛАХ здесь составляет +20 дБ/дек.

При w = 1 lg w = 0 , и ЛАХ пересечет горизонтальную ось.

3. Идеальное дифференцирующее звено (общий случай):

,

,

,

.

ЛАХ также будет представлять собой прямую с наклоном +20 дБ/дек и по сравнению с предыдущим примером будет проходить на 20 lgK децибел выше (рис.4).

Точка пересечения ЛАХ с горизонтальной осью может быть найдена из условия:

,

откуда , .

При w =1 значение ЛАХ составит L (1)=20 lg K .

4. Идеальное звено с передаточной функцией :

,

,

.

ЛАХ остается прямой линией, но ее наклон по сравнению с предыдущим случаем увеличится в 2 раза (рис. 5).

ЛАХ пересекает горизонтальную ось при , .

5. Идеальное интегрирующее звено:

,

,

,

.

ЛАХ остается прямой линией (рис.6). Ее приращение при изменении частоты в 10 раз составит:

дБ.

Наклон ЛАХ –20дБ/дек.

Точка пересечения ЛАХ с горизонтальной осью может быть найдена из условия:

.

При K =1 w 1 =1, при w 1 = K .

6. Звено с передаточной функцией :

,

,

.

ЛАХ – прямая линия, но ее наклон по сравнению с предыдущим примером увеличится в 3 раза и составит –60 дБ/дек (рис.7).

Точка пересечения ЛАХ с горизонтальной осью: , .

Нетрудно убедиться, что в общем случае для идеальных звеньев с передаточной функцией вида ЛАХ является прямой с наклоном 20 m дБ/дек и пересекает горизонтальную ось на частоте . При w =1 значение ЛАХ составляет 20 l g K . ЛФЧХ является горизонтальной прямой и проходит на уровне 90. m ° .

Для последующих примеров построение точных логарифмических характеристик возможно только на основе численного расчета, что не вызывает труда при использовании компьютера и программных средств типа MATLAB . Однако для решения практических задач большое значение имеют приемы их приближенного построения и прежде всего – построение асимптотической ЛАХ.

7. Звено с передаточной функцией W ( s )= Ts +1:

,

,

,

.

Графики точных логарифмических характеристик показаны на рис.8.

Асимптотическая ЛАХ может быть построена исходя из следующих соображений.

Вводится сопрягающая частота w с , исходя из условия равенства двух слагаемых, расположенных под корнем в выражении для ЛАХ: слагаемого, содержащего низшую степень частоты и слагаемого, содержащего высшую степень частоты.

Для рассматриваемого примера получим:

, .

Далее рассматриваются два диапазона частот.

Для низких частот, определяемых условием w w с , будет иметь место T w

.

Соответствующий этому выражению график – прямая, совпадающая с левой частью горизонтальной оси, является асимптотой точной ЛАХ при w ® 0 (рис.9).

Для высоких частот, определяемых условием w >> w с , будет иметь место T w >>1, и выражение для ЛАХ приближенно примет вид:

.

Учитывая результат, полученный в примере 3, нетрудно убедиться, что график этого выражения будет представлять собой прямую с наклоном +20дБ/дек (рис.9). Эта прямая является асимптотой точной ЛАХ при w ® ¥ . Она пересечет горизонтальную ось на частоте w 1 =1 / T , то есть асимптоты точной ЛАХ пересекаются на сопрягающей частоте.

Асимптотической ЛАХ называется ломаная линия, состоящая из отрезков асимптот точной ЛАХ. Абсолютная величина погрешности асимптотической ЛАХ по отношению к точной в рассматриваемом примере достигает максимума на сопрягающей частоте и составляет:

.

По мере удаления от сопрягающей частоты влево или вправо она снижается и на расстоянии 0,3 декады от сопрягающей частоты уменьшится примерно в 3 раза:

.

Также можно показать, что на расстоянии 0,5 декады от сопрягающей частоты погрешность уменьшится более, чем в 7 раз, а на расстоянии более декады от сопрягающей частоты будет пренебрежимо мала.

Отметим также некоторые свойства графика ЛФЧХ, соответствующего выражению arct g w T . Так как данное выражение входит в состав выражений для ЛФЧХ большинства более сложных звеньев и систем, эти свойства могут быть использованы для их приближенного анализа.

При w ® 0 асимптотой графика ЛФЧХ является горизонтальная прямая, проходящая через отметку 0 ° . При w ® ¥ асимптота – горизонтальная прямая, проходящая через отметку 90 ° .

На сопрягающей частоте 1/ T значение ЛФЧХ составляет 45 ° . Эта точка является центром симметрии всего графика (рис.10).

Полезно знать также следующие численные значения.

На расстоянии 0.3 декады от сопрягающей частоты ЛФЧХ получает приращение примерно ± 18,5 ° , и ее значения составляют 26,5 ° и 63,5 ° .

На расстоянии 0.5 декады от сопрягающей частоты ЛФЧХ получает приращение примерно ± 27,5 ° , и ее значения составляют 17,5 ° и 72,5 ° .

При удалении от сопрягающей частоты на декаду значение ЛФЧХ изменяется на 39.5 ° и составляет слева 5.5 ° и справа от сопрягающей частоты 84.5 ° .

На больших расстояниях от сопрягающей частоты значения ЛФЧХ изменяются медленно. В ряде случаев при приближенном анализе системы на частотах w 0.1 / T (на декаду и более левее сопрягающей) можно пренебречь значением arct g w T , а на частотах w >10 / T (на декаду и более правее сопрягающей) можно приближенно принять arct g w T » 90 ° .

8. Апериодическое звено 1-го порядка:

,

,

,

.

Примем сначала K =1. Рассмотрев, аналогично предыдущему примеру, низкие и высокие частоты, разделенные их сопрягающей частотой w с =1/ T , нетрудно получить асимптотическую ЛАХ (рис.11). Единственное отличие от предыдущего примера будет состоять в противоположном наклоне второго участка. Он составит –20 дБ/дек.

Слагаемое 20 l g K на всех частотах является константой. Следовательно, при K ¹ 1 весь график сместится вверх при K > 1 (20 l g K >0), а при K l g K 0).

Оценка погрешности асимптотической ЛАХ по отношению к точной аналогична полученной в предыдущем примере (рис.12).

Все результаты, полученные для ЛФЧХ, также сохраняются с учетом противоположного знака (рис. 12).

9. Апериодическое звено второго порядка ( T 1 = T 2 = T ):

,

,

,

.

Сравнивая выражения для ЛАХ, полученные в рассматриваемом и предыдущем примерах, можно сделать вывод о том, что различие в асимптотических ЛАХ будет состоять только в наклоне второго участка. Он увеличится в 2 раза и составит –40дБ/дек.

Максимальная погрешность асимптотической ЛАХ по отношению к точной в соответствии с принципом получения асимптотической ЛАХ также, очевидно, будет иметь место на сопрягающей частоте.

Значение асимптотической ЛАХ на сопрягающей частоте: L ас (1/ T )=20 lgK .

Значение точной ЛАХ на сопрягающей частоте:

.

Абсолютная величина погрешности составит дБ.

График ЛФЧХ и закономерности изменения ее значений будут аналогичны предыдущему примеру с учетом масштабного коэффициента 2.

Характеристики показаны на рис.13.

В общем случае для звена с передаточной функцией W ( s )= K ( Ts +1) m , где m =0, ± 1, ± 2, … получим следующие соотношения:

,

,

.

Отметим следующие закономерности:

— величина сопрягающей частоты, разделяющей участки асимптотической ЛАХ, w с =1/ T ,

— первый участок асимптотической ЛАХ горизонтален и проходит на уровне 20 l g K (при K =1совпадает с горизонтальной осью),

— наклон второго участка 20. m дБ/дек,

— абсолютная величина погрешности асимптотической ЛАХ по отношению к точной максимальна по сопрягающей частоте и составляет 3. m дБ,

— значение ЛФЧХ монотонно изменяется от 0 ° (при w ® 0) до 90 ° × m (при w ® ¥ ); на сопрягающей частоте ее значение составляет 45 ° × m ; эта точка является точкой симметрии всего графика ЛФЧХ.

10. Колебательное звено:

, 0 x

,

,

,

Рассмотрим построение асимптотической ЛАХ.

Под корнем в выражении для ЛАХ здесь присутствует несколько слагаемых. Тем не менее, принцип построения сохраняется. Сопрягающая частота находится из условия равенства двух слагаемых – содержащих низшую и высшую степень частоты:

, .

На низких частотах, w T , всеми слагаемыми, содержащими произведение w T , можно пренебречь по сравнению с единицей ( w T

.

Это уравнение горизонтальной прямой – асимптоты точной ЛАХ при w ® 0.

На высоких частотах, w >>1/ T , под корнем можно пренебречь всеми слагаемыми, кроме содержащего высшую степень частоты. Выражение для ЛАХ приближенно примет вид:

.

Это выражение для прямой с наклоном –40дБ/дек, причем при w T =1, то есть на сопрягающей частоте она проходит через точку с вертикальной координатой 20 l g K . Эта прямая является асимптотой точной ЛАХ при w ® ¥ . Здесь, как и в предыдущих примерах, асимптоты ЛАХ пересекаются на сопрягающей частоте (рис.14), что является общим правилом.

Закономерность формирования погрешностей асимптотической ЛАХ для колебательного звена является более сложной, чем в предыдущих примерах.

Прежде всего, оценим величину этой погрешности на сопрягающей частоте. Для асимптотической ЛАХ получим:

.

.

Величина погрешности зависит от величины x и изменяется от –6 дБ при x ® 1 до сколь угодно больших положительных значений при x ® 0.

Этот эффект обусловлен резонансными свойствами колебательного звена и в общем случае не позволяет при его анализе ограничиваться использованием только асимптотической ЛАХ.

Точные ЛАХ колебательного звена для различных значений x показаны на рис.14.

Из рис.14 видно, что резонансная частота, доставляющая максимум ЛАХ, отличается от сопрягающей. Резонансная частота w р может быть найдена из условия:

.

Общие рекомендации по использованию асимптотической ЛАХ для рассматриваемого примера сводятся к следующему:

— при больших значениях x , когда резонансный пик отсутствует или не превышает величины 3дБ, допустимо использование асимптотической ЛАХ;

— при малых x , когда высота резонансного пика превышает 3дБ, должна использоваться точная ЛАХ.

Значение x , обеспечивающее получение резонансного пика величиной 3дБ, после определения w р, может быть получено из условия:

.

Рекомендуется найти w р и величину x , обеспечивающую величину резонансного пика 3дБ, самостоятельно, а также убедиться в их независимости от параметров K и T .

Логарифмические фазо-частотные характеристики для различных x показаны на рис.15.

Рассмотрим правила построения асимптотических ЛАХ для более сложных передаточных функций на следующем примере:

,

где K =100с-2, T 1 =0.1с, T 2 =10с, T 3 =1с, T 4 =0.01с.

Выражения для АЧХ и точной ЛАХ будут иметь вид:

,

.

Наиболее распространенная в литературе рекомендация сводится к рассмотрению выражения для ЛАХ сложного звена как суммы выражений для ЛАХ рассмотренных выше звеньев, каждому из которых соответствует одна сопрягающая частота. При K =1 график асимптотической ЛАХ такого звена представлял бы собой кусочно-линейную характеристику, состоящую из низкочастотной асимптоты по горизонтальной оси и высокочастотной асимптоты с соответствующим наклоном, пересекающихся на сопрягающей частоте. Если общее выражение для ЛАХ записывать так, чтобы в отдельных слагаемых под знаком логарифма оставались выражения вида , то наклоны таких асимптот будут совпадать по величине с коэффициентами при . Результирующий график асимптотической ЛАХ может быть получен сложением графиков отдельных слагаемых.

Более удобным является предлагаемый ниже способ (при сохранении сформулированного правила записи выражения для ЛАХ). Он состоит в следующей последовательности действий.

1. Определяются сопрягающие частоты, соответствующие отдельным слагаемым, и записываются в порядке возрастания:

; ; ; .

2. Выбирается масштаб для оси частот так, чтобы крайние сопрягающие частоты располагались на расстоянии от 0.5 до 1 декады от краев видимой горизонтальной оси. Через сопрягающие частоты проводятся вертикальные пунктирные прямые (рис.16). Пунктирные прямые делят все поле графика на зоны, которым соответствуют отрезки различных асимптот ЛАХ (участки асимптотических ЛАХ). Построение асимптотической ЛАХ далее уже выполняется последовательно по участкам, начиная с первого.

3. Первый участок расположен левее всех сопрягающих частот. Следовательно, его уравнение, получаемое по условию w будет иметь вид:

.

Это уравнение прямой с наклоном –40 дБ/дек. Для ее построения необходимо найти опорные точки. Например:

— w =0.1, L (0.1)=20 l g 100-40 l g 0.1=40+40=80 дБ.

В качестве опорной может также использоваться точка пересечения данной прямой с горизонтальной осью, координаты которой могут быть найдены из условия L ( w 1 )=0:

,

, .

Отрезок прямой, выходящий за пределы соответствующего участка, показывают пунктирной линией (рис.17).

4. Второй участок расположен правее сопрягающей частоты 1/ T 2 , которой в выражении для ЛАХ соответствует коэффициент +40. По аналогии с рассмотренными выше примерами 7-9 можно придти к выводу, что наклон второго участка по сравнению с первым изменится на величину +40 дБ/дек. В результате второй участок окажется горизонтальным (рис.17).

5. Третий участок разделен со вторым сопрягающей частотой 1/ T 3 . Дополнительный наклон по отношению ко второму участку также соответствует коэффициенту в выражении для ЛАХ, связанному с этой сопрягающей частотой, и равен -60 дБ/дек.

Аналогично путем последовательного учета коэффициентов при соответствующих следующим сопрягающим частотам слагаемых в выражении для ЛАХ могут быть получены и наклоны остальных участков (рис.17).

Отметим еще раз, что непосредственное использование коэффициентов выражения для точной ЛАХ для расчета наклонов участков асимптотической ЛАХ возможно только при условии записи этого выражения так, чтобы частота под знаком логарифма имела первую степень.

Поскольку расстояние между сопрягающими частотами в рассматриваемом примере достаточно велико (1 декада) и сомножителя, вызывающего резонанс, в передаточной функции не содержится, погрешности асимптотической ЛАХ по отношению к точной будут достигать локальных максимумов на сопрягающих частотах, величины которых будут взаимно-однозначно связаны с величинами изменений наклонов ЛАХ (рис.18).

Рассмотрим следующий пример:

,

где K =200с-2, T 1 =0,08с, T 2 =0,5с, T 3 =20с, T 4 =40с.

Здесь в отличие от предыдущего примера, где вертикальные координаты границ участков ЛАХ определялись достаточно очевидно, для их определения потребуются дополнительные расчеты.

Запишем выражение для точной ЛАХ в соответствии со сформулированными выше рекомендациями:

.

Сопрягающие частоты в порядке возрастания:

; ; ; .

Первому участку асимптотической ЛАХ соответствует уравнение:

.

Первый участок – прямая с наклоном +20 дБ/дек.

Опорные точки первого участка:

— L ( w 1 )=0 при w 1 , определяемой из уравнения 20 l g K + 20 l g w 1 =20 l g K w 1 =0, откуда K w 1 =1, w 1 =1/ K =0,005.

Вертикальную координату границы первого участка можно определить непосредственно по его уравнению:

.

Наклон второго участка 20-20=0 дБ/дек (учитывается коэффициент при слагаемом, соответствующем сопрягающей частоте 1/ T 4 ). Участок горизонтален. Вертикальная координата его правой границы также 14 дБ.

Наклон третьего участка 0-20=-20 дБ/дек (учитывается коэффициент при слагаемом, соответствующем сопрягающей частоте 1/ T 3 ). Длина участка составляет l g 2- l g 0,05 » 0,3-(-1,3)=1,6 дек. Вертикальная координата его правой границы 14-20 × 1,6=14-32=-18 дБ.

Наклон четвертого участка –20-40=-60 дБ/дек (учитывается коэффициент при слагаемом, соответствующем сопрягающей частоте 1/ T 2 ). Длина участка l g 12,5- l g 2 » 1,1-0,3=0,8 дек. Вертикальная координата его правой границы примет значение -18-60 × 0,8= -18-48=-64 дБ.

Наклон пятого участка –60+20=-40 дБ/дек (учитывается коэффициент при слагаемом, соответствующем сопрягающей частоте 1/ T 1 ).

В рассматриваемом примере расстояние между сопрягающими частотами 1/ T 4 и 1/ T 3 , 1/ T 2 и 1/ T 1 не достигает декады. Поэтому погрешности асимптотической ЛАХ, связанные с сопрягающими частотами, будут более заметно, чем в предыдущем примере, накладываться друг на друга. В результате на сопрягающих частотах 1/ T 4 и 1/ T 3 погрешность асимптотической ЛАХ увеличится до 4 дБ, на сопрягающей частоте 1/ T 1 погрешность снизится до 2 дБ (рис. 19).